1. Introduction
Turbulent buoyant convection of fluid heated by a vertical wall is a classic fluid mechanics problem, for example seen when hot air rises next to the front of a convective heater used to warm an office or room. Whilst much early work on this problem was driven by engineering applications to industrial heating or cooling, the dynamics of these so-called vertical natural convection boundary layers is of contemporary relevance to diagnosing the impacts of climate change, and mitigation strategies from energy-efficient design. The ventilation and environmental comfort of buildings in which we live and work can be moderated by flows induced by warm, buoyant air rising near a hot wall of a building, or cold air sinking (e.g. Linden Reference Linden1999; Bonnebaigt, Caulfield & Linden Reference Bonnebaigt, Caulfield and Linden2018). Meanwhile, in Greenland and Antarctica the melting of steep glacier termini releases fresh and buoyant meltwater into the ocean, driving convective flow and enhancing heat transfer to the ice. Such convective boundary layers impact how ice sheets discharge ice mass and thus how sea levels respond to changing ocean temperatures (see reviews by Straneo & Cenedese Reference Straneo and Cenedese2015; Malyarenko et al. Reference Malyarenko, Wells, Langhorne, Robinson, Williams and Nicholls2020). The freshwater release also impacts ocean circulation and nutrient supply for marine ecological blooms.
As with many convection problems, it is important to understand how results from laboratory-scale experiments and state-of-the-art numerical simulations might be extrapolated to the more extreme scales present in some applications. For thermally driven convective flows, the magnitude of buoyant driving versus dissipation can be described by a Rayleigh number,  ${Ra} = g\alpha \Delta T L^3/\kappa \nu$, written in terms of the gravitational acceleration
${Ra} = g\alpha \Delta T L^3/\kappa \nu$, written in terms of the gravitational acceleration  $g$, imposed temperature difference
$g$, imposed temperature difference  $\Delta T$, thermal expansion coefficient
$\Delta T$, thermal expansion coefficient  $\alpha$, thermal diffusivity
$\alpha$, thermal diffusivity  $\kappa$, kinematic viscosity
$\kappa$, kinematic viscosity  $\nu$ and characteristic length scale
$\nu$ and characteristic length scale  $L$. Flows are alternatively characterised via a Grashof number
$L$. Flows are alternatively characterised via a Grashof number  ${Gr}={Ra}/{Pr}$ and Prandtl number
${Gr}={Ra}/{Pr}$ and Prandtl number  ${Pr}=\nu /\kappa$. There has been considerable interest in understanding how key properties such as the dimensionless heat flux, or Nusselt number
${Pr}=\nu /\kappa$. There has been considerable interest in understanding how key properties such as the dimensionless heat flux, or Nusselt number  ${Nu} =qL/k\Delta T$, vary with
${Nu} =qL/k\Delta T$, vary with  ${Ra}$ for turbulent flow (where
${Ra}$ for turbulent flow (where  $q$ is the heat flux from the wall and
$q$ is the heat flux from the wall and  $k$ the thermal conductivity). The key mechanisms have been debated at length for the related problem of Rayleigh–Bénard convection between hot and cold horizontal boundaries (Ahlers, Grossmann & Lohse Reference Ahlers, Grossmann and Lohse2009), where the boundary layers at the walls play a key role. Different theories for a classical regime feature the key ingredients of predominantly laminar boundary layers with the occasional buoyant detachment of plumes (see e.g. Howard Reference Howard1966; Grossmann & Lohse Reference Grossmann and Lohse2001, Reference Grossmann and Lohse2011), and predict scalings
$k$ the thermal conductivity). The key mechanisms have been debated at length for the related problem of Rayleigh–Bénard convection between hot and cold horizontal boundaries (Ahlers, Grossmann & Lohse Reference Ahlers, Grossmann and Lohse2009), where the boundary layers at the walls play a key role. Different theories for a classical regime feature the key ingredients of predominantly laminar boundary layers with the occasional buoyant detachment of plumes (see e.g. Howard Reference Howard1966; Grossmann & Lohse Reference Grossmann and Lohse2001, Reference Grossmann and Lohse2011), and predict scalings  ${Nu} \propto {Ra}^{\alpha }$ with
${Nu} \propto {Ra}^{\alpha }$ with  $\alpha \leq 1/3$ for moderate
$\alpha \leq 1/3$ for moderate  ${Pr}$. However, for large enough
${Pr}$. However, for large enough  ${Ra}$, the turbulent interior generates mean flows along the boundary that are sufficient for the boundary layers to become turbulent and dominated by shear (Kraichnan Reference Kraichnan1962; Grossmann & Lohse Reference Grossmann and Lohse2011). In this latter so-called ultimate regime, the heat flux is more efficient with an asymptotic
${Ra}$, the turbulent interior generates mean flows along the boundary that are sufficient for the boundary layers to become turbulent and dominated by shear (Kraichnan Reference Kraichnan1962; Grossmann & Lohse Reference Grossmann and Lohse2011). In this latter so-called ultimate regime, the heat flux is more efficient with an asymptotic  ${Nu} \propto {Ra}^{1/2}$ scaling predicted as
${Nu} \propto {Ra}^{1/2}$ scaling predicted as  ${Ra}\rightarrow \infty$ (to within logarithmic corrections, which lead to apparent scaling exponents
${Ra}\rightarrow \infty$ (to within logarithmic corrections, which lead to apparent scaling exponents  $1/3< \alpha \leq 1/2$ for the range of
$1/3< \alpha \leq 1/2$ for the range of  ${Ra}$ currently accessible in laboratory experiment or simulation).
${Ra}$ currently accessible in laboratory experiment or simulation).
The above dynamics finds a natural home for convective boundary layers at vertical walls, where buoyancy directly generates a mean flow along the walls. Early experiments and simulations with buoyancy supplied by a single vertical wall (see Papailiou (Reference Papailiou1991), Kerr & McConnochie (Reference Kerr and McConnochie2015), Nakao, Hattori & Suto (Reference Nakao, Hattori and Suto2017) and references therein) are consistent with a classical scaling  ${Nu} \propto {Ra}^{1/3}$, and with theories for a buoyancy-driven sublayer near the wall (George & Capp Reference George and Capp1979; Hölling & Herwig Reference Hölling and Herwig2005; Wells & Worster Reference Wells and Worster2008). But shear-dominated dynamics has been hypothesised for vertical boundary layers at large
${Nu} \propto {Ra}^{1/3}$, and with theories for a buoyancy-driven sublayer near the wall (George & Capp Reference George and Capp1979; Hölling & Herwig Reference Hölling and Herwig2005; Wells & Worster Reference Wells and Worster2008). But shear-dominated dynamics has been hypothesised for vertical boundary layers at large  ${Ra}$ (Wells & Worster Reference Wells and Worster2008), building on ideas for the ultimate regime of Rayleigh–Bénard convection. For convective channel flow between hot and cold vertical boundaries, hints of incipient ultimate-regime behaviour are seen from statistics conditionally averaged over regions of high shear (Ng et al. Reference Ng, Ooi, Lohse and Chung2017). A transition to shear-dominated heat transfer is also seen in experiments that inject a buoyant plume to supplement a convective boundary layer (McConnochie & Kerr Reference McConnochie and Kerr2017). But how might the shear-dominated regime develop for convection at a single heated wall? Beyond its fundamental interest, this question has important implications: extrapolating classical and ultimate regime scalings to the geophysical scale of a glacier terminus can lead to predicted melt rates differing by a factor of up to 10 (Wells & Worster Reference Wells and Worster2008).
${Ra}$ (Wells & Worster Reference Wells and Worster2008), building on ideas for the ultimate regime of Rayleigh–Bénard convection. For convective channel flow between hot and cold vertical boundaries, hints of incipient ultimate-regime behaviour are seen from statistics conditionally averaged over regions of high shear (Ng et al. Reference Ng, Ooi, Lohse and Chung2017). A transition to shear-dominated heat transfer is also seen in experiments that inject a buoyant plume to supplement a convective boundary layer (McConnochie & Kerr Reference McConnochie and Kerr2017). But how might the shear-dominated regime develop for convection at a single heated wall? Beyond its fundamental interest, this question has important implications: extrapolating classical and ultimate regime scalings to the geophysical scale of a glacier terminus can lead to predicted melt rates differing by a factor of up to 10 (Wells & Worster Reference Wells and Worster2008).
2. Overview
Ke et al. (Reference Ke, Williamson, Armfield and Komiya2023) explore the mechanisms for the regime transition in turbulent boundary-layer dynamics for a transiently developing flow from a heated wall. They consider a vertically periodic numerical domain, building on their previous direct numerical simulations of this configuration (Ke et al. Reference Ke, Williamson, Armfield, Norris and Komiya2020, Reference Ke, Williamson, Armfield, Komiya and Norris2021). Identifying the length scale  $L$ with the boundary-layer thickness, this suite of simulations suggests that the dimensionless heat flux scales as
$L$ with the boundary-layer thickness, this suite of simulations suggests that the dimensionless heat flux scales as  ${Nu}\propto {Gr}^{1/3} \propto {Ra}^{1/3}$ for intermediate
${Nu}\propto {Gr}^{1/3} \propto {Ra}^{1/3}$ for intermediate  ${Gr}$, consistent with previous scalings in the classical regime. However,
${Gr}$, consistent with previous scalings in the classical regime. However,  ${Nu} \propto {Gr}^{0.381}$ for
${Nu} \propto {Gr}^{0.381}$ for  $10^7\leq {Gr} \leq 10^8$, consistent with ultimate-regime heat transfer with logarithmic corrections.
$10^7\leq {Gr} \leq 10^8$, consistent with ultimate-regime heat transfer with logarithmic corrections.
By probing the underlying differences in boundary-layer structure, Ke et al. (Reference Ke, Williamson, Armfield and Komiya2023) provide further evidence to support this suggestion of the ultimate heat-transfer scaling, with a key role for inner and outer shear layers in the mean flow along the wall (see figure 1). For the classical regime at intermediate  ${Gr}$, shear production dominates the turbulent kinetic energy budget in the outer shear layer, but with low turbulent production in a relatively laminar near-wall shear layer. The buoyancy flux from the wall plays a key role in driving the mean flow, but appears less significant in the production of turbulent kinetic energy. Transitioning into the ultimate regime, a second peak of turbulent kinetic energy develops in the inner shear layer with enhanced shear production and the growth of turbulent Reynolds stresses in this inner region. Several features develop that are commonly seen in pure shear flows. Longitudinal streaks develop in the near-wall region for large
${Gr}$, shear production dominates the turbulent kinetic energy budget in the outer shear layer, but with low turbulent production in a relatively laminar near-wall shear layer. The buoyancy flux from the wall plays a key role in driving the mean flow, but appears less significant in the production of turbulent kinetic energy. Transitioning into the ultimate regime, a second peak of turbulent kinetic energy develops in the inner shear layer with enhanced shear production and the growth of turbulent Reynolds stresses in this inner region. Several features develop that are commonly seen in pure shear flows. Longitudinal streaks develop in the near-wall region for large  ${Gr}$, with a wavelength commensurate with that observed for canonical turbulent shear flows. The wall drag coefficient transitions from a laminar scaling to one consistent with a turbulent logarithmic layer, coincident with a transition in estimated viscous sublayer thickness. The usual logarithmic profile of velocity in a shear flow is, however, modified to account for buoyancy from a logarithmic variation of mean temperature, and the ratio of turbulent production to dissipation is larger than for a pure shear flow. The combined package provides evidence of a transition from a classical heat-transfer regime with an inner laminar flow driven by buoyancy to an ultimate heat-transfer regime where shear-driven instabilities generate a turbulent inner region of the boundary layer.
${Gr}$, with a wavelength commensurate with that observed for canonical turbulent shear flows. The wall drag coefficient transitions from a laminar scaling to one consistent with a turbulent logarithmic layer, coincident with a transition in estimated viscous sublayer thickness. The usual logarithmic profile of velocity in a shear flow is, however, modified to account for buoyancy from a logarithmic variation of mean temperature, and the ratio of turbulent production to dissipation is larger than for a pure shear flow. The combined package provides evidence of a transition from a classical heat-transfer regime with an inner laminar flow driven by buoyancy to an ultimate heat-transfer regime where shear-driven instabilities generate a turbulent inner region of the boundary layer.
3. Future
The mechanistic evidence of a regime transition presented by Ke et al. (Reference Ke, Williamson, Armfield and Komiya2023) provides insight to guide the description of convective boundary-layer processes at more extreme scales. Many ice-sheet and ocean models exploit heat transfer scalings consistent with a shear-controlled ultimate regime (Malyarenko et al. Reference Malyarenko, Wells, Langhorne, Robinson, Williams and Nicholls2020), but for convective flows at steep ice faces this will only be accurate after sufficient flow develops to exceed the transitional value of  ${Gr}$. Whilst one would expect a similar pattern of flow dynamics, an immediate query is whether the transitional
${Gr}$. Whilst one would expect a similar pattern of flow dynamics, an immediate query is whether the transitional  ${Gr}$ for transiently developing flow with translation symmetry will apply directly to spatially developing flows with along-flow gradients. Ice melting in salty ocean water also features two-component flow with Prandtl and Schmidt numbers much larger than the value,
${Gr}$ for transiently developing flow with translation symmetry will apply directly to spatially developing flows with along-flow gradients. Ice melting in salty ocean water also features two-component flow with Prandtl and Schmidt numbers much larger than the value,  ${Pr}=0.71$, considered by Ke et al. (Reference Ke, Williamson, Armfield and Komiya2023), which will impact boundary-layer development (Howland, Verzicco & Lohse Reference Howland, Verzicco and Lohse2023). A further factor for glacial melting is the ocean density stratification, which can generate layering of the flow (Huppert & Turner Reference Huppert and Turner1978) or detrainment from the boundary layer (Bonnebaigt et al. Reference Bonnebaigt, Caulfield and Linden2018). Such detrainment can also be relevant to convection through thermal gradients in building ventilation (Bonnebaigt et al. Reference Bonnebaigt, Caulfield and Linden2018).
${Pr}=0.71$, considered by Ke et al. (Reference Ke, Williamson, Armfield and Komiya2023), which will impact boundary-layer development (Howland, Verzicco & Lohse Reference Howland, Verzicco and Lohse2023). A further factor for glacial melting is the ocean density stratification, which can generate layering of the flow (Huppert & Turner Reference Huppert and Turner1978) or detrainment from the boundary layer (Bonnebaigt et al. Reference Bonnebaigt, Caulfield and Linden2018). Such detrainment can also be relevant to convection through thermal gradients in building ventilation (Bonnebaigt et al. Reference Bonnebaigt, Caulfield and Linden2018).
For engineering applications, the results presented by Ke et al. (Reference Ke, Williamson, Armfield and Komiya2023) may offer insight into flow control strategies to optimise heat transfer. The ultimate regime has higher efficiency of heat transfer and appears to arise from instability and the production of turbulence in the inner shear layer in the near-wall flow. This instability might be manipulated to promote or delay the transition to the ultimate regime. The detailed investigation of the transition from the classical to ultimate regime by Ke et al. (Reference Ke, Williamson, Armfield and Komiya2023) offers potential for improved characterisation and control of vertical natural convection boundary layers.
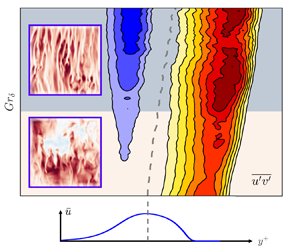

 $\bar {U}$ and temperature
$\bar {U}$ and temperature  $\bar {T}$ varying with distance
$\bar {T}$ varying with distance  $y$ from the wall (upper row) and Reynolds stresses
$y$ from the wall (upper row) and Reynolds stresses  $\overline {u'v'}$ (lower row) for convection from a wall at hotter temperature
$\overline {u'v'}$ (lower row) for convection from a wall at hotter temperature  $T_w$ than the far-field temperature
$T_w$ than the far-field temperature  $T_{\infty }$. (a) Classical regime and (b) ultimate regime.
$T_{\infty }$. (a) Classical regime and (b) ultimate regime.
1. Introduction
Turbulent buoyant convection of fluid heated by a vertical wall is a classic fluid mechanics problem, for example seen when hot air rises next to the front of a convective heater used to warm an office or room. Whilst much early work on this problem was driven by engineering applications to industrial heating or cooling, the dynamics of these so-called vertical natural convection boundary layers is of contemporary relevance to diagnosing the impacts of climate change, and mitigation strategies from energy-efficient design. The ventilation and environmental comfort of buildings in which we live and work can be moderated by flows induced by warm, buoyant air rising near a hot wall of a building, or cold air sinking (e.g. Linden Reference Linden1999; Bonnebaigt, Caulfield & Linden Reference Bonnebaigt, Caulfield and Linden2018). Meanwhile, in Greenland and Antarctica the melting of steep glacier termini releases fresh and buoyant meltwater into the ocean, driving convective flow and enhancing heat transfer to the ice. Such convective boundary layers impact how ice sheets discharge ice mass and thus how sea levels respond to changing ocean temperatures (see reviews by Straneo & Cenedese Reference Straneo and Cenedese2015; Malyarenko et al. Reference Malyarenko, Wells, Langhorne, Robinson, Williams and Nicholls2020). The freshwater release also impacts ocean circulation and nutrient supply for marine ecological blooms.
As with many convection problems, it is important to understand how results from laboratory-scale experiments and state-of-the-art numerical simulations might be extrapolated to the more extreme scales present in some applications. For thermally driven convective flows, the magnitude of buoyant driving versus dissipation can be described by a Rayleigh number, ${Ra} = g\alpha \Delta T L^3/\kappa \nu$, written in terms of the gravitational acceleration
${Ra} = g\alpha \Delta T L^3/\kappa \nu$, written in terms of the gravitational acceleration  $g$, imposed temperature difference
$g$, imposed temperature difference  $\Delta T$, thermal expansion coefficient
$\Delta T$, thermal expansion coefficient  $\alpha$, thermal diffusivity
$\alpha$, thermal diffusivity  $\kappa$, kinematic viscosity
$\kappa$, kinematic viscosity  $\nu$ and characteristic length scale
$\nu$ and characteristic length scale  $L$. Flows are alternatively characterised via a Grashof number
$L$. Flows are alternatively characterised via a Grashof number  ${Gr}={Ra}/{Pr}$ and Prandtl number
${Gr}={Ra}/{Pr}$ and Prandtl number  ${Pr}=\nu /\kappa$. There has been considerable interest in understanding how key properties such as the dimensionless heat flux, or Nusselt number
${Pr}=\nu /\kappa$. There has been considerable interest in understanding how key properties such as the dimensionless heat flux, or Nusselt number  ${Nu} =qL/k\Delta T$, vary with
${Nu} =qL/k\Delta T$, vary with  ${Ra}$ for turbulent flow (where
${Ra}$ for turbulent flow (where  $q$ is the heat flux from the wall and
$q$ is the heat flux from the wall and  $k$ the thermal conductivity). The key mechanisms have been debated at length for the related problem of Rayleigh–Bénard convection between hot and cold horizontal boundaries (Ahlers, Grossmann & Lohse Reference Ahlers, Grossmann and Lohse2009), where the boundary layers at the walls play a key role. Different theories for a classical regime feature the key ingredients of predominantly laminar boundary layers with the occasional buoyant detachment of plumes (see e.g. Howard Reference Howard1966; Grossmann & Lohse Reference Grossmann and Lohse2001, Reference Grossmann and Lohse2011), and predict scalings
$k$ the thermal conductivity). The key mechanisms have been debated at length for the related problem of Rayleigh–Bénard convection between hot and cold horizontal boundaries (Ahlers, Grossmann & Lohse Reference Ahlers, Grossmann and Lohse2009), where the boundary layers at the walls play a key role. Different theories for a classical regime feature the key ingredients of predominantly laminar boundary layers with the occasional buoyant detachment of plumes (see e.g. Howard Reference Howard1966; Grossmann & Lohse Reference Grossmann and Lohse2001, Reference Grossmann and Lohse2011), and predict scalings  ${Nu} \propto {Ra}^{\alpha }$ with
${Nu} \propto {Ra}^{\alpha }$ with  $\alpha \leq 1/3$ for moderate
$\alpha \leq 1/3$ for moderate  ${Pr}$. However, for large enough
${Pr}$. However, for large enough  ${Ra}$, the turbulent interior generates mean flows along the boundary that are sufficient for the boundary layers to become turbulent and dominated by shear (Kraichnan Reference Kraichnan1962; Grossmann & Lohse Reference Grossmann and Lohse2011). In this latter so-called ultimate regime, the heat flux is more efficient with an asymptotic
${Ra}$, the turbulent interior generates mean flows along the boundary that are sufficient for the boundary layers to become turbulent and dominated by shear (Kraichnan Reference Kraichnan1962; Grossmann & Lohse Reference Grossmann and Lohse2011). In this latter so-called ultimate regime, the heat flux is more efficient with an asymptotic  ${Nu} \propto {Ra}^{1/2}$ scaling predicted as
${Nu} \propto {Ra}^{1/2}$ scaling predicted as  ${Ra}\rightarrow \infty$ (to within logarithmic corrections, which lead to apparent scaling exponents
${Ra}\rightarrow \infty$ (to within logarithmic corrections, which lead to apparent scaling exponents  $1/3< \alpha \leq 1/2$ for the range of
$1/3< \alpha \leq 1/2$ for the range of  ${Ra}$ currently accessible in laboratory experiment or simulation).
${Ra}$ currently accessible in laboratory experiment or simulation).
The above dynamics finds a natural home for convective boundary layers at vertical walls, where buoyancy directly generates a mean flow along the walls. Early experiments and simulations with buoyancy supplied by a single vertical wall (see Papailiou (Reference Papailiou1991), Kerr & McConnochie (Reference Kerr and McConnochie2015), Nakao, Hattori & Suto (Reference Nakao, Hattori and Suto2017) and references therein) are consistent with a classical scaling ${Nu} \propto {Ra}^{1/3}$, and with theories for a buoyancy-driven sublayer near the wall (George & Capp Reference George and Capp1979; Hölling & Herwig Reference Hölling and Herwig2005; Wells & Worster Reference Wells and Worster2008). But shear-dominated dynamics has been hypothesised for vertical boundary layers at large
${Nu} \propto {Ra}^{1/3}$, and with theories for a buoyancy-driven sublayer near the wall (George & Capp Reference George and Capp1979; Hölling & Herwig Reference Hölling and Herwig2005; Wells & Worster Reference Wells and Worster2008). But shear-dominated dynamics has been hypothesised for vertical boundary layers at large  ${Ra}$ (Wells & Worster Reference Wells and Worster2008), building on ideas for the ultimate regime of Rayleigh–Bénard convection. For convective channel flow between hot and cold vertical boundaries, hints of incipient ultimate-regime behaviour are seen from statistics conditionally averaged over regions of high shear (Ng et al. Reference Ng, Ooi, Lohse and Chung2017). A transition to shear-dominated heat transfer is also seen in experiments that inject a buoyant plume to supplement a convective boundary layer (McConnochie & Kerr Reference McConnochie and Kerr2017). But how might the shear-dominated regime develop for convection at a single heated wall? Beyond its fundamental interest, this question has important implications: extrapolating classical and ultimate regime scalings to the geophysical scale of a glacier terminus can lead to predicted melt rates differing by a factor of up to 10 (Wells & Worster Reference Wells and Worster2008).
${Ra}$ (Wells & Worster Reference Wells and Worster2008), building on ideas for the ultimate regime of Rayleigh–Bénard convection. For convective channel flow between hot and cold vertical boundaries, hints of incipient ultimate-regime behaviour are seen from statistics conditionally averaged over regions of high shear (Ng et al. Reference Ng, Ooi, Lohse and Chung2017). A transition to shear-dominated heat transfer is also seen in experiments that inject a buoyant plume to supplement a convective boundary layer (McConnochie & Kerr Reference McConnochie and Kerr2017). But how might the shear-dominated regime develop for convection at a single heated wall? Beyond its fundamental interest, this question has important implications: extrapolating classical and ultimate regime scalings to the geophysical scale of a glacier terminus can lead to predicted melt rates differing by a factor of up to 10 (Wells & Worster Reference Wells and Worster2008).
2. Overview
Ke et al. (Reference Ke, Williamson, Armfield and Komiya2023) explore the mechanisms for the regime transition in turbulent boundary-layer dynamics for a transiently developing flow from a heated wall. They consider a vertically periodic numerical domain, building on their previous direct numerical simulations of this configuration (Ke et al. Reference Ke, Williamson, Armfield, Norris and Komiya2020, Reference Ke, Williamson, Armfield, Komiya and Norris2021). Identifying the length scale $L$ with the boundary-layer thickness, this suite of simulations suggests that the dimensionless heat flux scales as
$L$ with the boundary-layer thickness, this suite of simulations suggests that the dimensionless heat flux scales as  ${Nu}\propto {Gr}^{1/3} \propto {Ra}^{1/3}$ for intermediate
${Nu}\propto {Gr}^{1/3} \propto {Ra}^{1/3}$ for intermediate  ${Gr}$, consistent with previous scalings in the classical regime. However,
${Gr}$, consistent with previous scalings in the classical regime. However,  ${Nu} \propto {Gr}^{0.381}$ for
${Nu} \propto {Gr}^{0.381}$ for  $10^7\leq {Gr} \leq 10^8$, consistent with ultimate-regime heat transfer with logarithmic corrections.
$10^7\leq {Gr} \leq 10^8$, consistent with ultimate-regime heat transfer with logarithmic corrections.
By probing the underlying differences in boundary-layer structure, Ke et al. (Reference Ke, Williamson, Armfield and Komiya2023) provide further evidence to support this suggestion of the ultimate heat-transfer scaling, with a key role for inner and outer shear layers in the mean flow along the wall (see figure 1). For the classical regime at intermediate ${Gr}$, shear production dominates the turbulent kinetic energy budget in the outer shear layer, but with low turbulent production in a relatively laminar near-wall shear layer. The buoyancy flux from the wall plays a key role in driving the mean flow, but appears less significant in the production of turbulent kinetic energy. Transitioning into the ultimate regime, a second peak of turbulent kinetic energy develops in the inner shear layer with enhanced shear production and the growth of turbulent Reynolds stresses in this inner region. Several features develop that are commonly seen in pure shear flows. Longitudinal streaks develop in the near-wall region for large
${Gr}$, shear production dominates the turbulent kinetic energy budget in the outer shear layer, but with low turbulent production in a relatively laminar near-wall shear layer. The buoyancy flux from the wall plays a key role in driving the mean flow, but appears less significant in the production of turbulent kinetic energy. Transitioning into the ultimate regime, a second peak of turbulent kinetic energy develops in the inner shear layer with enhanced shear production and the growth of turbulent Reynolds stresses in this inner region. Several features develop that are commonly seen in pure shear flows. Longitudinal streaks develop in the near-wall region for large  ${Gr}$, with a wavelength commensurate with that observed for canonical turbulent shear flows. The wall drag coefficient transitions from a laminar scaling to one consistent with a turbulent logarithmic layer, coincident with a transition in estimated viscous sublayer thickness. The usual logarithmic profile of velocity in a shear flow is, however, modified to account for buoyancy from a logarithmic variation of mean temperature, and the ratio of turbulent production to dissipation is larger than for a pure shear flow. The combined package provides evidence of a transition from a classical heat-transfer regime with an inner laminar flow driven by buoyancy to an ultimate heat-transfer regime where shear-driven instabilities generate a turbulent inner region of the boundary layer.
${Gr}$, with a wavelength commensurate with that observed for canonical turbulent shear flows. The wall drag coefficient transitions from a laminar scaling to one consistent with a turbulent logarithmic layer, coincident with a transition in estimated viscous sublayer thickness. The usual logarithmic profile of velocity in a shear flow is, however, modified to account for buoyancy from a logarithmic variation of mean temperature, and the ratio of turbulent production to dissipation is larger than for a pure shear flow. The combined package provides evidence of a transition from a classical heat-transfer regime with an inner laminar flow driven by buoyancy to an ultimate heat-transfer regime where shear-driven instabilities generate a turbulent inner region of the boundary layer.
Figure 1. Schematic of mean profiles of vertical velocity $\bar {U}$ and temperature
$\bar {U}$ and temperature  $\bar {T}$ varying with distance
$\bar {T}$ varying with distance  $y$ from the wall (upper row) and Reynolds stresses
$y$ from the wall (upper row) and Reynolds stresses  $\overline {u'v'}$ (lower row) for convection from a wall at hotter temperature
$\overline {u'v'}$ (lower row) for convection from a wall at hotter temperature  $T_w$ than the far-field temperature
$T_w$ than the far-field temperature  $T_{\infty }$. (a) Classical regime and (b) ultimate regime.
$T_{\infty }$. (a) Classical regime and (b) ultimate regime.
3. Future
The mechanistic evidence of a regime transition presented by Ke et al. (Reference Ke, Williamson, Armfield and Komiya2023) provides insight to guide the description of convective boundary-layer processes at more extreme scales. Many ice-sheet and ocean models exploit heat transfer scalings consistent with a shear-controlled ultimate regime (Malyarenko et al. Reference Malyarenko, Wells, Langhorne, Robinson, Williams and Nicholls2020), but for convective flows at steep ice faces this will only be accurate after sufficient flow develops to exceed the transitional value of ${Gr}$. Whilst one would expect a similar pattern of flow dynamics, an immediate query is whether the transitional
${Gr}$. Whilst one would expect a similar pattern of flow dynamics, an immediate query is whether the transitional  ${Gr}$ for transiently developing flow with translation symmetry will apply directly to spatially developing flows with along-flow gradients. Ice melting in salty ocean water also features two-component flow with Prandtl and Schmidt numbers much larger than the value,
${Gr}$ for transiently developing flow with translation symmetry will apply directly to spatially developing flows with along-flow gradients. Ice melting in salty ocean water also features two-component flow with Prandtl and Schmidt numbers much larger than the value,  ${Pr}=0.71$, considered by Ke et al. (Reference Ke, Williamson, Armfield and Komiya2023), which will impact boundary-layer development (Howland, Verzicco & Lohse Reference Howland, Verzicco and Lohse2023). A further factor for glacial melting is the ocean density stratification, which can generate layering of the flow (Huppert & Turner Reference Huppert and Turner1978) or detrainment from the boundary layer (Bonnebaigt et al. Reference Bonnebaigt, Caulfield and Linden2018). Such detrainment can also be relevant to convection through thermal gradients in building ventilation (Bonnebaigt et al. Reference Bonnebaigt, Caulfield and Linden2018).
${Pr}=0.71$, considered by Ke et al. (Reference Ke, Williamson, Armfield and Komiya2023), which will impact boundary-layer development (Howland, Verzicco & Lohse Reference Howland, Verzicco and Lohse2023). A further factor for glacial melting is the ocean density stratification, which can generate layering of the flow (Huppert & Turner Reference Huppert and Turner1978) or detrainment from the boundary layer (Bonnebaigt et al. Reference Bonnebaigt, Caulfield and Linden2018). Such detrainment can also be relevant to convection through thermal gradients in building ventilation (Bonnebaigt et al. Reference Bonnebaigt, Caulfield and Linden2018).
For engineering applications, the results presented by Ke et al. (Reference Ke, Williamson, Armfield and Komiya2023) may offer insight into flow control strategies to optimise heat transfer. The ultimate regime has higher efficiency of heat transfer and appears to arise from instability and the production of turbulence in the inner shear layer in the near-wall flow. This instability might be manipulated to promote or delay the transition to the ultimate regime. The detailed investigation of the transition from the classical to ultimate regime by Ke et al. (Reference Ke, Williamson, Armfield and Komiya2023) offers potential for improved characterisation and control of vertical natural convection boundary layers.
Acknowledgements
A.J.W. thanks the authors of Ke et al. (Reference Ke, Williamson, Armfield and Komiya2023) and editor J. Neufeld for feedback.
Declaration of interests
The author reports no conflict of interest.