Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-24T14:06:12.031Z Has data issue: false hasContentIssue false
  • English
  • Français

Flow and passive transport in planar multipolar flows

Published online by Cambridge University Press:  02 November 2018

M. A. Zouache Open the ORCID record for M. A. Zouache [Opens in a new window] ,
I. Eames Open the ORCID record for I. Eames [Opens in a new window] ,
C. A. Klettner Open the ORCID record for C. A. Klettner [Opens in a new window]  and
P. J. Luthert
M. A. Zouache*
Affiliation:
Institute of Ophthalmology, University College London, London EC1V 9EL, UK
I. Eames
Affiliation:
Department of Mechanical Engineering, University College London, WC1E 7JE, UK
C. A. Klettner
Affiliation:
Department of Mechanical Engineering, University College London, WC1E 7JE, UK
P. J. Luthert
Affiliation:
Institute of Ophthalmology, University College London, London EC1V 9EL, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the flow and transport of heat or mass, modelled as passive scalars, within a basic geometrical unit of a three-dimensional multipolar flow – a triangular prism – characterised by a side length 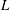$L$, a normalised thickness 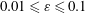$0.01\leqslant \unicode[STIX]{x1D700}\leqslant 0.1$ and an apex angle 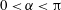$0<\unicode[STIX]{x1D6FC}<\unicode[STIX]{x03C0}$, and connected to inlet and outlet pipes of equal normalised radius 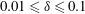$0.01\leqslant \unicode[STIX]{x1D6FF}\leqslant 0.1$ perpendicularly to the plane of the flow. The flow and scalar fields are investigated over the range 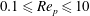$0.1\leqslant Re_{p}\leqslant 10$ and 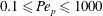$0.1\leqslant Pe_{p}\leqslant 1000$, where 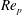$Re_{p}$ and 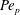$Pe_{p}$ are respectively the Reynolds and Péclet numbers imposed at the inlet pipe when either a Dirichlet (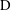$\text{D}$) or a Neumann (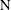$\text{N}$) scalar boundary condition is imposed at the wall unattached to the inlets and outlets. A scalar no-flux boundary condition is imposed at all the other walls. An axisymmetric model is applied to understand the flow and scalar transport in the inlet and outlet regions, which consist of a turning region close to the pipe centreline and a channel region away from it. A separate two-dimensional model is then developed for the channel region by solving the integral form of the momentum and scalar advection–diffusion equations. Analytical relations between geometrical, flow and scalar transport parameters based on similarity and integral methods are generated and agree closely with numerical solutions. Finally, three-dimensional numerical calculations are undertaken to test the validity of the axisymmetric and depth-averaged analyses. Dominant flow and scalar transport features vary dramatically across the flow domain. In the turning region, the flow is a largely irrotational straining flow when 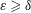$\unicode[STIX]{x1D700}\geqslant \unicode[STIX]{x1D6FF}$ and a dominantly viscous straining flow when 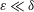$\unicode[STIX]{x1D700}\ll \unicode[STIX]{x1D6FF}$. The thickness of the scalar boundary layer scales to the local Péclet number to the power 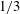$1/3$. 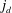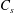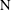The diffusive flux $j_{d}$ and the scalar $C_{s}$ at the wall where ($\text{D}$) or ($\text{N}$) is imposed, respectively, are constant. In the channel region, the flow is parabolic and dominated by a source flow near the inlet and an irrotational straining flow away from it. When 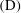$(\text{D})$ is imposed the scalar decreases exponentially with distance from the inlet and the normalised scalar transfer coefficient converges to 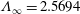$\unicode[STIX]{x1D6EC}_{\infty }=2.5694$. When 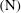$(\text{N})$ is imposed, 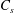$C_{s}$ varies proportionally to surface area. Transport in the straining region downstream of the inlet is diffusion-limited, and 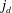$j_{d}$ and 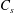$C_{s}$ are functions of the geometrical parameters 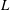$L$, $\unicode[STIX]{x1D700}$, $\unicode[STIX]{x1D6FC}$ and 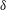$\unicode[STIX]{x1D6FF}$. In addition to describing the fundamental properties of the flow and passive transport in multipolar configurations, the present work demonstrates how geometrical and flow parameters should be set to control transfers in the different regions of the flow domain.

JFM classification

Low-Reynolds-number flows: Hele-Shaw flows Low-Reynolds-number flows: Low-Reynolds-number flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 858 , 10 January 2019 , pp. 184 - 227
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. A. 1972 Handbook of Mathematical Functions: with Formulas, Graphs, and Mathematical Tables, 9th printing. Dover.Google Scholar
Acrivos, A. 1962 The asymptotic form of the laminar boundary-layer mass-transfer rate for large interfacial velocities. J. Fluid Mech. 12, 337–357.Google Scholar
Batchelor, G. K. 1957 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Bejan, A. 2013 Convection Heat Transfer, 4th edn. John Wiley & Sons.Google Scholar
Camera-Roda, G., Boi, C., Saavedra, A. & Sarti, G. C. 1994 Heat and mass transfer boundary layers in radial creeping flow. Intl J. Heat Mass Transfer 37 (14), 2145–2153.Google Scholar
Chatterjee, A. 1993 An infinite series solution for the creeping radial entrance flow of a Newtonian fluid. AIChE J. 39 (9), 1563–1568.Google Scholar
Chatterjee, A. 2000 Newtonian radial entrance flow. AIChE J. 46 (3), 462–475.Google Scholar
Chatterjee, A. & Deviprasath, L. J. 2001 Heat transfer in confined laminar axisymmetric impinging jets at small nozzle-plate distances: the role of upstream vorticity diffusion. Numer. Heat Transfer 39 (8), 777–800.Google Scholar
Chatterjee, A. & White, D. 1989 Radial entry flow of a newtonian fluid. J. Phys. D: Appl. Phys. 22, 915–924.Google Scholar
Chatwin, P. C. 1975 On the longitudinal dispersion of passive contaminant in oscillatory flow in tubes. J. Fluid Mech. 71, 513–527.Google Scholar
Chen, J.-D. 1987 Radial viscous fingering patterns in Hele-Shaw cells. Exp. Fluids 5, 363–371.Google Scholar
Chen, J.-D. 1989 Growth of radial viscous fingers in a Hele-Shaw cell. J. Fluid Mech. 201, 223–242.Google Scholar
Cooper, R. J., Billingham, J. & King, A. C. 2000 Flow and reaction in solid oxide fuel cells. J. Fluid Mech. 411, 233–262.Google Scholar
Daccord, G., Nittman, J. & Stanley, H. E. 1986 Radial viscous fingers and diffusion-limited aggregration: fractal dimension and growth sites. Phys. Rev. Lett. 56 (4), 336–339.Google Scholar
Detry, J. G., Deroanne, C., Sindic, M. & Jensen, B. B. B. 2009 Laminar flow in radial flow cell with small aspect ratios: numerical and experimental study. Chem. Engng Sci. 64, 31–42.Google Scholar
Detry, J. G., Rouxhet, P. G., Boulangé-Petermann, L., Deroanne, C. & Sindic, M. 2007 Cleanability assessment of model solid surfaces with a radial-flow cell. Colloids Surf. A 302, 540–548.Google Scholar
Duda, J. L. & Vrentas, J. S. 1971 Heat transfer in a cylindrical cavity. J. Fluid Mech. 45, 261–279.Google Scholar
Eames, I. 1999 A hundred years of Hele-Shaw’s analogue computer. Math. Today 85–88.Google Scholar
Elkouh, A. F. 1967 Inertial effects in laminar radial flow between parallel plates. Intl J. Mech. Sci. 9, 253–255.Google Scholar
Fryer, P. J., Slater, N. K. H. & Duddridge, J. E. 1985 Suggestions for the operation of radial flow cells in cell adhesion and biofouling studies. Biotechnol. Bioengng 27, 434–438.Google Scholar
Gersten, K. 1973 Die kompressible Grenzschichtströmung am dreidimensionalen Staupunkt bei starkem Absaugen oder Ausblasen. Wärme- Stoffübertrag. 1, 52–61.Google Scholar
Gersten, K. & Körner, H. 1968 Wärmeübergang unter Berücksichtigung der Reibungswärme bei laminaren Keil-Strömungen mit Veränderlicher Temperatur und Normalgeschwindigkeit Entlang der Wand. Intl J. Heat Mass Transfer 11, 655–673.Google Scholar
Geuzaine, C. & Remacle, J.-F. 2009 Gmsh: a three-dimensional finite element mesh generator with built-in pre- and post-processing facilities. Intl J. Numer. Meth. Engng 79 (11), 1309–1331.Google Scholar
Goldstein, A. S. & Di-Milla, P. A. 1996 Application of fluid mechanic and kinetic models to characterize mammalian cell detachment in radial-flow chamber. Biotechnol. Bioengng 55, 616–629.Google Scholar
Hagiwara, T. 1962 Studies on the characteristics of radial flow nozzles. Trans. Japan Soc. Mech. Engrs 28 (186), 138–144.Google Scholar
Haugh, L. M., Linsenmeier, R. A. & Goldstick, T. K. 1990 Mathematical models of the spatial distribution of retinal oxygen tension and consumption, including changes upon illumination. Ann. Biomed. Engng 18, 19–36.Google Scholar
Hele-Shaw, H. S. 1884 The theory of continuous calculating machines, and of a mechanism on a new principle for this and other purposes. Proc. R. Soc. Lond. 37, 189–191.Google Scholar
Hele-Shaw, H. S. 1898 Flow of water. Nature 58 (1489), 34–36.Google Scholar
Hewitt, J. M. & McKenzie, D. P. 1975 Dissipative heating in convective flows. J. Fluid Mech. 68, 721–738.Google Scholar
Homann, F. 1936 Der Einfluß großer Zähigkeit bei der Strömung um den Zylinder und um die Kugel. Z. Angew. Math. Mech. 16 (3), 153–164.Google Scholar
Howarth, L. 1951 Cxliv. the boundary layer in three-dimensional flow. – Part II. The flow near a stagnation point. Lond. Edinb. Dubl. Phil. Mag.: Series 7 42 (335), 1433–1440.Google Scholar
Howison, S. D. 1986 Fingering in Hele-Shaw cells. J. Fluid Mech. 167, 439–453.Google Scholar
Hunt, J. B. & Torbe, I. 1962 Characteristics of a hydrostatic thrust bearing. Intl J. Mech. Sci. 4, 503–516.Google Scholar
Ishizawa, S. 1965 The axi-symmetric laminar flow in an arbitrarily shaped narrow gap. 1st Report, Theoretical analysis for the inlet region. Bull. JSME 8 (31), 353–367.Google Scholar
Ishizawa, S. 1966 The axi-symmetric laminar flow in an arbitrarily shaped narrow gap. 2nd Report, Theoretical analysis for the downstream region. Bull. JSME 9 (33), 86–103.Google Scholar
Jackson, J. D. & Symmons, G. R. 1965a An investigation of laminar radial flow between two parallel discs. Appl. Sci. Res. A 15 (1), 59–75.Google Scholar
Jackson, J. D. & Symmons, G. R. 1965b The pressure distribution in a hydrostatic thrust bearing. Intl J. Mech. Sci. 7, 239–242.Google Scholar
Kamal, M. R. & Kenig, S. 1972a The injection molding of thermoplastics. Part I: Theoretical model. Polym. Engng Sci. 12, 294–301.Google Scholar
Kamal, M. R. & Kenig, S. 1972b The injection molding of thermoplastics. Part II. Experimental test of the model. Polym. Engng Sci. 12, 302–308.Google Scholar
von Kármán, T. 1921 Über laminare und turbulented Reibung. Z. Angew. Math. Mech. 1, 233–252.Google Scholar
Kellogg, O. D. 1929 Foundations of Potential Theory. Verlag Von Julius Springer.Google Scholar
Klettner, C. A., Eames, I., Semsarzadeh, S. & Nicolle, A. 2016 The effect of a uniform through-surface flow on a cylinder and sphere. J. Fluid Mech. 793, 798–839.Google Scholar
Koplik, J., Redner, S. & Hinch, E. J. 1994 Tracer dispersion in planar multipole flows. Phys. Rev. E 50 (6), 4650–4671.Google Scholar
Kurowski, P., Ippolito, I., Hulin, J. P., Koplik, J. & Hinch, E. J. 1994 Anomalous dispersion in a dipole flow geometry. Phys. Fluids 6, 108–117.Google Scholar
Lee, P.-M. & Lin, S. 1985 Pressure distribution for radial inflow between narrowly spaced disks. Trans. ASME J. Fluids Engng 107 (107), 338–341.Google Scholar
Libby, P. A. 1967 Heat and mass transfer at a general three-dimensional stagnation point. AIAA J. 5 (3), 507–517.Google Scholar
Livesey, J. L. 1960 Inertia effects in viscous flows. Intl J. Mech. Sci. 1, 84–88.Google Scholar
Moller, P. S.1963 Radial flow without swirl between parallel disks. Master’s thesis, Department of Mechanical Engineering, McGill University, Montreal, Canada.Google Scholar
Moller, P. S. 1966 A radial diffuser using incompressible flow between narrowly spaced disks. Trans. ASME J. Basic Engng 88 (1), 155–162.Google Scholar
Mukhopadhyay, A. 2009 Analytical solutions of Nusselt number for thermally developing radial flows through small gap between two parallel disks. Trans. ASME J. Heat Transfer 131 (5), 1–4.Google Scholar
Nakabayashi, N., Ichikawa, T. & Morinishi, Y. 2002 Size of annular separation bubble around the inlet corner and viscous flow structure between two parallel disks. Exp. Fluids 32, 425–433.Google Scholar
Nicolle, A. & Eames, I. 2011 Numerical study of flow through and around a circular array of cylinders. J. Fluid Mech. 679, 1–31.Google Scholar
Ockendon, H. & Ockendon, J. R. 1977 Variable-viscosity flows in heated and cooled channels. J. Fluid Mech. 83 (1), 177–190.Google Scholar
Osterle, J. F. & Hughes, W. R. 1958 The effect of lubricant inertia in hydrostatic thrust-bearing lubrication. Wear 1 (6), 465–471.Google Scholar
Owen, P. R. & Thomson, W. R. 1962 Heat transfer across rough surfaces. J. Fluid Mech. 15, 321–334.Google Scholar
Paterson, L. 1981 Radial fingering in a Hele-Shaw cell. J. Fluid Mech. 113, 513–529.Google Scholar
Paterson, L. 1985 Fingering with miscible fluids in a Hele-Shaw cell. Phys. Fluids 28, 26–30.Google Scholar
Pinkus, O. & Sternlicht, B. 1961 Theory of Hydrodynamic Lubrication. McGraw-Hill Book.Google Scholar
Pohlhausen, K. 1921 Zur näherungsweisen Integration der Differentialgleichung der laminaren Grenzschicht. Z. Angew. Math. Mech. 1, 252–268.Google Scholar
Potter, M. C. & Graber, E. 1972 Stability of plane Poiseuille flow with heat transfer. Phys. Fluids 15 (1), 387–391.Google Scholar
Prandtl, L. 1904 Über Flussigkeitsbewegung bei sehr kleiner Reibung. Verhandlungen des III, Internationalen Mathematiker-Kongresses Heidelberg, pp. 484–491. B. G. Teubner.Google Scholar
Prata, A. T., Pilichi, C. D. M. & Ferreira, R. T. S. 1995 Local heat transfer in axially feeding radial flow between parallel disks. Trans. ASME J. Heat Transfer 117, 47–53.Google Scholar
Qasaimeh, M. A., Gervais, T. & Juncker, D. 2011 Microfluidic quadrupole and floating concentration gradient. Nat. Commun. 2, 464.Google Scholar
Raal, J. D. 1978 Radial source flow between parallel disks. J. Fluid Mech. 85, 401–416.Google Scholar
Rauseo, S. N., Barnes, P. D. Jr & Maher, J. V. 1987 Development of radial fingering patterns. Phys. Rev. A 35 (3), 1245–1251.Google Scholar
Reynolds, O. 1886 On the theory of lubrication and its application to Mr. Beauchamp tower’s experiment, including an experimental determination of the viscosity of olive oil. Phil. Trans. R. Soc. Lond. 177, 157–235.Google Scholar
Richardson, S. 1972 Hele-Shaw flows with a free boundary produced by the injection of fluid into a narrow channel. J. Fluid Mech. 56, 609–618.Google Scholar
Richardson, S. 1981 Some Hele-Shaw flows with time-dependent free boundaries. J. Fluid Mech. 102, 263–278.Google Scholar
Sameen, A. & Govindarajan, R. 2007 The effect of wall heating on instability of channel flow. J. Fluid Mech. 577, 417–442.Google Scholar
Savage, S. B. 1964 Laminar radial flow between parallel plates. J. Appl. Mech. 31, 594–596.Google Scholar
Scholtz, M. T. & Trass, O. 1970 Mass transfer in a nonuniform impinging jet. Part II. Boundary layer flow-mass transfer. AIChE J. 16 (1), 90–96.Google Scholar
Shäfer, P. & Herwig, H. 1993 Stability of plane Poiseuille flow with temperature dependent viscosity. Intl J. Heat Mass Transfer 36 (9), 2441–2448.Google Scholar
Shah, R. K. & London, A. L. 1978 Laminar Flow Forced Convection in Ducts. Academic Press.Google Scholar
Stevenson, J. F. 1976 Heat and mass transfer in radial flow. Chem. Engng Sci. 31 (12), 1225–1226.Google Scholar
Stewart, W. E. & Prober, R. 1962 Heat transfer and diffusion in wedge flows with rapid mass transfers. Intl J. Heat Mass Transfer 5, 1149–1163.Google Scholar
Wall, D. P. & Nagata, M. 2000 Nonlinear equilibrium solutions for the channel flow of fluid with temperature-dependent viscosity. J. Fluid Mech. 406, 1–26.Google Scholar
Wall, D. P. & Wilson, S. K. 1996 The linear stability of channel flow of fluid with temperature-dependent viscosity. J. Fluid Mech. 323, 107–132.Google Scholar
Woolard, H. W. 1957 A theoretical analysis of the viscous flow in a narrowly spaced radial diffuser. Trans. ASME J. Appl. Mech. 24 (1), 9–15.Google Scholar
Yao, L.-S. & Berger, S. A. 1978 Flow in heated curved pipes. J. Fluid Mech. 88, 339–354.Google Scholar
Zhang, M. & Koplik, J. 1997 Tracer dispersion in three-dimensional multipole flows. Phys. Rev. E 56 (4), 4244–4258.Google Scholar
Zouache, M. A., Eames, I., Klettner, C. A. & Luthert, P. J. 2016 Form, shape and function: segmented blood flow in the choriocapillaris. Sci. Rep. 6, 35754.Google Scholar
Zouache, M. A., Eames, I. & Luthert, P. J. 2015 Blood flow in the choriocapillaris. J. Fluid Mech. 774, 37–66.Google Scholar