Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-27T23:24:48.907Z Has data issue: false hasContentIssue false
  • English
  • Français

The evolution of a front in turbulent thermal wind balance. Part 2. Numerical simulations

Published online by Cambridge University Press:  09 October 2019

Matthew N. Crowe  and
John R. Taylor Open the ORCID record for John R. Taylor [Opens in a new window]
Matthew N. Crowe
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
John R. Taylor*
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In Crowe & Taylor (J. Fluid Mech., vol. 850, 2018, pp. 179–211) we described a theory for the evolution of density fronts in a rotating reference frame subject to strong vertical mixing using an asymptotic expansion in small Rossby number, 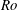$Ro$. We found that the front reaches a balanced state where vertical diffusion is balanced by horizontal advection in the buoyancy equation. The depth-averaged buoyancy obeys a nonlinear diffusion equation which admits a similarity solution corresponding to horizontal spreading of the front. Here we use numerical simulations of the full momentum and buoyancy equations to investigate this problem for a wide range of Rossby and Ekman numbers. We examine the accuracy of our asymptotic solution and find that many aspects of the solution are valid for 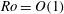$Ro=O(1)$. However, the asymptotic solution departs from the numerical simulations for small Ekman numbers where the dominant balance in the momentum equation changes. We trace the source of this discrepancy to a depth-independent geostrophic flow that develops on both sides of the front and we develop a modification to the theory described in Crowe & Taylor (2018) to account for this geostrophic flow. The refined theory closely matches the numerical simulations, even for 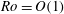$Ro=O(1)$. Finally, we develop a new scaling for the intense vertical velocity that can develop in thin bands at the edges of the front.

JFM classification

Geophysical and Geological Flows: Ocean circulation Geophysical and Geological Flows: Ocean processes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 880 , 10 December 2019 , pp. 326 - 352
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bachman, S. D., Fox-Kemper, B., Taylor, J. R. & Thomas, L. N. 2017 Parameterization of frontal symmetric instabilities. I. Theory for resolved fronts. Ocean Model. 109, 72–95.Google Scholar
Bachman, S. D. & Taylor, J. R. 2016 Numerical simulations of the equilibrium between eddy-induced restratification and vertical mixing. J. Phys. Oceanogr. 46 (3), 919–935.Google Scholar
Blumen, W. 2000 Inertial oscillations and frontogenesis in a zero potential vorticity model. J. Phys. Oceanogr. 30, 31–39.10.1175/1520-0485(2000)030<0031:IOAFIA>2.0.CO;22.0.CO;2>Google Scholar
Capet, X., McWilliams, J. C., Molemaker, M. J. & Shchepetkin, A. F. 2008 Mesoscale to submesoscale transition in the california current system. Part II. Frontal processes. J. Phys. Oceanogr. 38, 44–64.Google Scholar
Charney, J. G. 1973 Planetary Fluid Dynamics. chap. Symmetric Circulations in Idealized Models, pp. 128–141. D. Reidel Publishing Company.Google Scholar
Crowe, M. N. & Taylor, J. R. 2018 The evolution of a front in turbulent thermal wind balance. Part 1. Theory. J. Fluid Mech. 850, 179–211.10.1017/jfm.2018.448Google Scholar
Eliassen, A. 1962 On the vertical circulation in frontal zones. Geofys. Publ. 24 (4), 147–160.Google Scholar
Erdogan, M. E. & Chatwin, P. C. 1967 The effects of curvature and buoyancy on the laminar dispersion of solute in a horizontal tube. J. Fluid Mech. 29, 465–484.Google Scholar
Ferrari, R. 2011 A frontal challenge for climate models. Science 332 (6027), 316–317.Google Scholar
Fox-Kemper, B., Danabasoglu, G., Ferrari, R., Griffies, S. M., Hallberg, R. W., Holland, M. M., Maltrud, M. E., Peacock, S. & Samuels, B. L. 2011 Parameterization of mixed layer eddies. III. Implementation and impact in global ocean climate simulations. Ocean Model. 39 (1–2), 61–78.Google Scholar
Fox-Kemper, B., Ferrari, R. & Hallberg, R. 2008 Parameterization of mixed layer eddies. Part I. Theory and diagnosis. J. Phys. Oceanogr. 38 (6), 1145–1165.Google Scholar
Garrett, C. J. R. & Loder, J. W. 1981 Dynamical aspects of shallow sea fronts. Phil. Trans. R. Soc. Lond. A 302, 563–581.Google Scholar
Gula, J., Molemaker, M. J. & McWilliams, J. C. 2014 Submesoscale cold filaments in the gulf stream. J. Phys. Oceanogr. 44, 2617–2643.Google Scholar
Holton, J. R. & Hakim, G. J. 2012 An Introduction to Dynamic Meteorology, vol. 88. Academic Press.Google Scholar
Hoskins, B. J. & Bretherton, F. P. 1972 Atmospheric frontogenesis models: mathematical formulation and solution. J. Atmos. Sci. 29, 11–37.Google Scholar
Mahadevan, A. & Tandon, A. 2006 An analysis of mechanisms for submesoscale vertical motion at ocean fronts. Ocean Model. 14 (3–4), 241–256.10.1016/j.ocemod.2006.05.006Google Scholar
McWilliams, J. C. 2017 Submesoscale surface fronts and filaments: secondary circulation, buoyancy flux, and frontogenesis. J. Fluid Mech. 823, 391–432.Google Scholar
Niiler, P. P. 1969 On the Ekman divergence in an oceanic jet. J. Geophys. Res. 74 (28), 7048–7052.Google Scholar
Orlanski, I. & Ross, B. B. 1977 The circulation associated with a cold front. Part I. Dry case. J. Atmos. Sci. 34, 1619–1633.Google Scholar
Rudnick, D. L. & Luyten, J. R. 1996 Intensive surveys of the azores front. 1. Tracers and dynamics. J. Geophys. Res. 101, 923–939.Google Scholar
Shakespeare, C. J. & Taylor, J. R. 2013 A generalized mathematical model of geostrophic adjustment and frontogenesis: uniform potential vorticity. J. Fluid Mech. 736, 366–413.Google Scholar
Smith, R. 1982 Similarity solutions of a non-linear diffusion equation. IMA J. Appl. Maths 28 (2), 149–160.Google Scholar
Stern, M. E. 1965 Interaction of a uniform wind stress with a geostrophie vortex. Deep-Sea Res. 12, 355–367.Google Scholar
Sullivan, P. P. & McWilliams, J. C. 2018 Frontogenesis and frontal arrest of a dense filament in the oceanic surface boundary layer. J. Fluid Mech. 837, 1341–1380.Google Scholar
Taylor, J. R.2008 Numerical simulations of the stratified oceanic bottom boundary layer. PhD thesis, University of California, San Diego, CA.Google Scholar
Taylor, J. R. & Ferrari, R. 2010 Buoyancy and wind-driven convection at mixed layer density fronts. J. Phys. Oceanogr. 40, 1222–1242.Google Scholar
Thomas, L. N. & Lee, C. M. 2005 Intensification of ocean fronts by down-front winds. J. Phys. Oceanogr. 35, 1086–1102.Google Scholar
Thompson, L. A. 2000 Ekman layers and two-dimensional frontogenesis in the upper ocean. J. Geophys. Res. 105 (C3), 6437–6451.Google Scholar