Published online by Cambridge University Press: 22 March 2017
We examine the transient evolution of a negatively buoyant, laminar plume in an emptying filling box containing a uniform porous medium. In the long time limit,
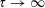 $\unicode[STIX]{x1D70F}\rightarrow \infty$
, the box is partitioned into two uniform layers of different densities. However, the approach towards steady state is characterized by a lower contaminated layer that is continuously stratified. The presence of this continuous stratification poses non-trivial analytical challenges; we nonetheless demonstrate that it is possible to derive meaningful bounds on the range of possible solutions, particularly in the limit of large
$\unicode[STIX]{x1D70F}\rightarrow \infty$
, the box is partitioned into two uniform layers of different densities. However, the approach towards steady state is characterized by a lower contaminated layer that is continuously stratified. The presence of this continuous stratification poses non-trivial analytical challenges; we nonetheless demonstrate that it is possible to derive meaningful bounds on the range of possible solutions, particularly in the limit of large
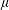 $\unicode[STIX]{x1D707}$
, where
$\unicode[STIX]{x1D707}$
, where
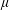 $\unicode[STIX]{x1D707}$
represents the ratio of the draining to filling time scales. The validity of our approach is confirmed by drawing comparisons against the free turbulent plume case where, unlike with porous media plumes, an analytical solution that accounts for the time-variable continuous stratification of the lower layer is available (Baines & Turner, J. Fluid Mech., vol. 37, 1969, pp. 51–80; Germeles, J. Fluid Mech., vol. 71, 1975, pp. 601–623). A separate component of our study considers time-variable forcing where the laminar plume source strength changes abruptly with time. When the source is turned on and off with a half-period,
$\unicode[STIX]{x1D707}$
represents the ratio of the draining to filling time scales. The validity of our approach is confirmed by drawing comparisons against the free turbulent plume case where, unlike with porous media plumes, an analytical solution that accounts for the time-variable continuous stratification of the lower layer is available (Baines & Turner, J. Fluid Mech., vol. 37, 1969, pp. 51–80; Germeles, J. Fluid Mech., vol. 71, 1975, pp. 601–623). A separate component of our study considers time-variable forcing where the laminar plume source strength changes abruptly with time. When the source is turned on and off with a half-period,
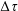 $\unicode[STIX]{x0394}\unicode[STIX]{x1D70F}$
, the depth and reduced gravity of the contaminated layer oscillate between two extrema after the first few cycles. Different behaviour is seen when the source is merely turned up or down. For instance, a change of the source reduced gravity leads to a permanent change of interface depth, which is a qualitative point of difference from the free turbulent plume case.
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70F}$
, the depth and reduced gravity of the contaminated layer oscillate between two extrema after the first few cycles. Different behaviour is seen when the source is merely turned up or down. For instance, a change of the source reduced gravity leads to a permanent change of interface depth, which is a qualitative point of difference from the free turbulent plume case.