Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-24T03:28:21.206Z Has data issue: false hasContentIssue false
  • English
  • Français

Dispersion of inertial particles in cellular flows in the small-Stokes, large-Péclet regime

Published online by Cambridge University Press:  17 September 2020

Antoine Renaud Open the ORCID record for Antoine Renaud [Opens in a new window]  and
Jacques Vanneste Open the ORCID record for Jacques Vanneste [Opens in a new window]
Antoine Renaud
Affiliation:
School of Mathematics and Maxwell Institute for Mathematical Sciences, University of Edinburgh, King's Buildings, EdinburghEH9 3FD, UK
Jacques Vanneste*
Affiliation:
School of Mathematics and Maxwell Institute for Mathematical Sciences, University of Edinburgh, King's Buildings, EdinburghEH9 3FD, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

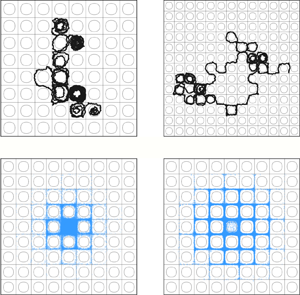
We investigate the transport of inertial particles by cellular flows when advection dominates over inertia and diffusion, that is, for Stokes and Péclet numbers satisfying $St \ll 1$ and $Pe \gg 1$. Starting from the Maxey–Riley model, we consider the distinguished scaling $St \, Pe = O(1)$ and derive an effective Brownian dynamics approximating the full Langevin dynamics. We then apply homogenisation and matched-asymptotics techniques to obtain an explicit expression for the effective diffusivity $\bar {D}$ characterising long-time dispersion. This expression quantifies how $\bar {D}$, proportional to $Pe^{-1/2}$ when inertia is neglected, increases for particles heavier than the fluid and decreases for lighter particles. In particular, when $St \gg Pe^{-1}$, we find that $\bar {D}$ is proportional to $St^{1/2}/(\log ( St \, Pe))^{1/2}$ for heavy particles and exponentially small in $St \, Pe$ for light particles. We verify our asymptotic predictions against numerical simulations of the particle dynamics.

JFM classification

Mathematical Foundations: General fluid mechanics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 903 , 25 November 2020 , A2
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Auton, T. R., Hunt, J. C. R. & Prud'Homme, M. 1988 The force exerted on a body in inviscid unsteady non-uniform rotational flow. J. Fluid Mech. 197, 241–257.CrossRefGoogle Scholar
Childress, S. 1979 Alpha-effect in flux ropes and sheets. Phys. Earth Planet. Inter. 20 (2), 172–180.CrossRefGoogle Scholar
Childress, S. & Soward, A. M. 1989 Scalar transport and alpha-effect for a family of cat's-eye flows. J. Fluid Mech. 205, 99–133.CrossRefGoogle Scholar
Daitche, A. & Tél, T. 2011 Memory effects are relevant for chaotic advection of inertial particles. Phys. Rev. Lett. 107, 244501.CrossRefGoogle ScholarPubMed
DLMF 2019 NIST Digital Library of Mathematical Functions. http://dlmf.nist.gov/, Release 1.0.24 of 2019-09-15, f. (ed. Olver, W. J., Olde Daalhuis, A. B., Lozier, D. W., Schneider, B. I., Boisvert, R. F., Clark, C. W., Miller, B. R., Saunders, B. V., Cohl, H. S. & McClain, M. A.).Google Scholar
Evans, L. C. 2013 An Introduction to Stochastic Differential Equations. American Mathematical Society.CrossRefGoogle Scholar
Ferry, J. & Balachandar, S. 2001 A fast Eulerian method for disperse two-phase flow. Intl J. Multiphase Flow 27 (7), 1199–1226.CrossRefGoogle Scholar
Freidlin, M. & Wentzell, A. 2012 Random Perturbations of Dynamical Systems, 3rd edn.Springer.CrossRefGoogle Scholar
Haller, G. & Sapsis, T. 2008 Where do inertial particles go in fluid flows? Physica D 237 (5), 573–583.CrossRefGoogle Scholar
Haynes, P. H. & Vanneste, J. 2014 Dispersion in the large-deviation regime. Part 2: cellular flow at large Péclet number. J. Fluid Mech. 745, 351–377.CrossRefGoogle Scholar
Heinze, S. 2003 Diffusion-advection in cellular flows with large Péclet numbers. Arch. Rat. Mech. Anal. 168, 329–342.CrossRefGoogle Scholar
Langlois, G. P., Farazmand, M. & Haller, G. 2015 Asymptotic dynamics of inertial particles with memory. J. Nonlinear Sci. 25, 1225–1255.CrossRefGoogle Scholar
Majda, A. J. & Kramer, P. R. 1999 Simplified models for turbulent diffusion: theory, numerical modelling, and physical phenomena. Phys. Rep. 314 (4), 237–574.CrossRefGoogle Scholar
Manton, M. J. 1974 On the motion of a small particle in the atmosphere. Boundary-Layer Meteorol. 6, 487–504.CrossRefGoogle Scholar
Martins Afonso, M., Mazzino, A. & Muratore-Ginanneschi, P. 2012 Eddy diffusivities of inertial particles under gravity. J. Fluid Mech. 694, 426–463.CrossRefGoogle Scholar
Maxey, M. R. & Riley, J. J. 1983 Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 26 (4), 883–889.CrossRefGoogle Scholar
Novikov, A., Papanicolaou, G. & Ryzhik, L. 2005 Boundary layers for cellular flows at high Péclet numbers. Commun. Pure Appl. Maths 867–922, 563–580.Google Scholar
Pavliotis, G. A. & Stuart, A. M. 2005 Periodic homogenization for inertial particles. Physica D 204 (3), 161–187.CrossRefGoogle Scholar
Pavliotis, G. A., Stuart, A. M. & Band, L. 2006 Monte Carlo studies of effective diffusivities for inertial particles. In Monte Carlo and Quasi-Monte Carlo Methods 2004 (ed. Niederreiter, H. & Talay, D.), pp. 431–441. Springer.CrossRefGoogle Scholar
Pavliotis, G. A., Stuart, A. M. & Zygalakis, K. C. 2009 Calculating effective diffusivities in the limit of vanishing molecular diffusion. J. Comput. Phys. 228 (4), 1030–1055.CrossRefGoogle Scholar
Rosenbluth, M. N., Berk, H. L., Doxas, I. & Horton, W. 1987 Effective diffusion in laminar convective flows. Phys. Fluids 30 (9), 2636–2647.CrossRefGoogle Scholar
Rubin, J., Jones, C. K. R. T. & Maxey, M. 1995 Settling and asymptotic motion of aerosol particles in a cellular flow field. J. Nonlinear Sci. 5 (4), 337–358.CrossRefGoogle Scholar
Sapsis, T. & Haller, G. 2010 Clustering criterion for inertial particles in two-dimensional time-periodic and three-dimensional steady flows. Chaos 20 (1), 017515.CrossRefGoogle ScholarPubMed
Shraiman, B. I. 1987 Diffusive transport in a Rayleigh–Bénard convection cell. Phys. Rev. A 36, 261–267.CrossRefGoogle Scholar
Soward, A. M. 1987 Fast dynamo action in a steady flow. J. Fluid Mech. 180, 267–295.CrossRefGoogle Scholar
Vergassola, M. & Avellaneda, M. 1997 Scalar transport in compressible flow. Physica D 106 (1), 148–166.CrossRefGoogle Scholar