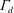 $\unicode[STIX]{x1D6E4}_{d}$ and its implications for an emptying–filling box
$\unicode[STIX]{x1D6E4}_{d}$ and its implications for an emptying–filling boxPublished online by Cambridge University Press: 16 March 2017
The natural ventilation flow driven by an internal buoyant plume in a box involving an upper opening (vent) located at the ceiling (for the outflow) and a large lower opening at the floor (for the inflow) is examined theoretically in a general non-Boussinesq case. Analytical solutions of this emptying–filling box problem allow the characteristics of the flow at the vent to be determined. From these characteristics, a non-dimensional parameter
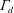 $\unicode[STIX]{x1D6E4}_{d}$
(called the discharge plume parameter) is expressed. This parameter characterizes the initial balance of volume, buoyancy and momentum fluxes in the plume-like flow that forms above the vent. We then note that the value of
$\unicode[STIX]{x1D6E4}_{d}$
(called the discharge plume parameter) is expressed. This parameter characterizes the initial balance of volume, buoyancy and momentum fluxes in the plume-like flow that forms above the vent. We then note that the value of
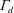 $\unicode[STIX]{x1D6E4}_{d}$
allows the buoyant fluid layer depth in the box to be estimated, which is a new and interesting result for natural ventilation problems. Following previous experimental results, the decrease of the vent discharge coefficient
$\unicode[STIX]{x1D6E4}_{d}$
allows the buoyant fluid layer depth in the box to be estimated, which is a new and interesting result for natural ventilation problems. Following previous experimental results, the decrease of the vent discharge coefficient
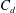 $C_{d}$
when
$C_{d}$
when
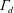 $\unicode[STIX]{x1D6E4}_{d}$
increases is discussed and a theoretical model based on plume necking is proposed. The emptying–filling box model is then extended for a variable
$\unicode[STIX]{x1D6E4}_{d}$
increases is discussed and a theoretical model based on plume necking is proposed. The emptying–filling box model is then extended for a variable
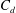 $C_{d}$
(depending on
$C_{d}$
(depending on
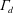 $\unicode[STIX]{x1D6E4}_{d}$
). Even though the discharge coefficient may be markedly reduced at high values of
$\unicode[STIX]{x1D6E4}_{d}$
). Even though the discharge coefficient may be markedly reduced at high values of
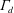 $\unicode[STIX]{x1D6E4}_{d}$
, our results show that this only affects transients and the steady state of an emptying–filling box for relatively thin buoyant fluid layers.
$\unicode[STIX]{x1D6E4}_{d}$
, our results show that this only affects transients and the steady state of an emptying–filling box for relatively thin buoyant fluid layers.