Published online by Cambridge University Press: 01 June 2017
The flow in a rectangular channel with walls made of polyacrylamide gel is experimentally studied to examine the effect of soft walls on transition and turbulence. The bottom wall is fixed to a substrate and the top wall is unrestrained. As the Reynolds number increases, two different flow regimes are observed. The first is the ‘soft-wall turbulence’ (Srinivas & Kumaran, J. Fluid Mech., vol. 780, 2015, pp. 649–686). There is a large increase in the magnitudes of the velocity fluctuations after transition and the fluid velocity fluctuations appear to be non-zero at the soft walls, although higher resolution measurements are required to establish the nature of the boundary dynamics. The fluid velocity fluctuations are symmetric about the centreline of the channel, and they show relatively little downstream variation. The wall displacement measurements indicate that there is no observable motion perpendicular to the surface to within the experimental resolution, but displacement fluctuations parallel to the surface are observed after transition. As the Reynolds number is further increased, there is a second ‘wall-flutter’ transition, which involves visible downstream travelling waves in the top (unrestrained) wall alone. Wall displacement fluctuations of frequency less than approximately 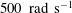 $500~\text{rad}~\text{s}^{-1}$ are observed both parallel and perpendicular to the wall. The mean velocity profiles and turbulence intensities are asymmetric, with much larger turbulence intensities near the top wall. The transitions are observed in sequence from a laminar flow at Reynolds number less than 1000 for a channel of height 0.6 mm and from a turbulent flow at a Reynolds number greater than 1000 for a channel of height 1.8 mm.
$500~\text{rad}~\text{s}^{-1}$ are observed both parallel and perpendicular to the wall. The mean velocity profiles and turbulence intensities are asymmetric, with much larger turbulence intensities near the top wall. The transitions are observed in sequence from a laminar flow at Reynolds number less than 1000 for a channel of height 0.6 mm and from a turbulent flow at a Reynolds number greater than 1000 for a channel of height 1.8 mm.