Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ostilla-Mónico, R.
2017.
Mixed thermal conditions in convection: how do continents affect the mantle’s circulation?.
Journal of Fluid Mechanics,
Vol. 822,
Issue. ,
p.
1.
Hayat, Tasawar
Rashid, Madiha
and
Alsaedi, Ahmed
2017.
MHD convective flow of magnetite-Fe3O4 nanoparticles by curved stretching sheet.
Results in Physics,
Vol. 7,
Issue. ,
p.
3107.
Yang, Yantao
Verzicco, Roberto
and
Lohse, Detlef
2018.
Two-scalar turbulent Rayleigh–Bénard convection: numerical simulations and unifying theory.
Journal of Fluid Mechanics,
Vol. 848,
Issue. ,
p.
648.
Bakhuis, Dennis
Ostilla-Mónico, Rodolfo
van der Poel, Erwin P.
Verzicco, Roberto
and
Lohse, Detlef
2018.
Mixed insulating and conducting thermal boundary conditions in Rayleigh–Bénard convection.
Journal of Fluid Mechanics,
Vol. 835,
Issue. ,
p.
491.
Nandukumar, Yada
Chakraborty, Suman
Verma, Mahendra K.
and
Lakkaraju, Rajaram
2019.
On heat transport and energy partition in thermal convection with mixed boundary conditions.
Physics of Fluids,
Vol. 31,
Issue. 6,
Ostilla-Mónico, Rodolfo
and
Amritkar, Amit
2020.
Regime crossover in Rayleigh–Bénard convection with mixed boundary conditions.
Journal of Fluid Mechanics,
Vol. 903,
Issue. ,
Zhang, Lu
Ding, Guang-Yu
and
Xia, Ke-Qing
2021.
On the effective horizontal buoyancy in turbulent thermal convection generated by cell tilting.
Journal of Fluid Mechanics,
Vol. 914,
Issue. ,
Li, Xiao-Ming
He, Ji-Dong
Tian, Ye
Hao, Peng
and
Huang, Shi-Di
2021.
Effects of Prandtl number in quasi-two-dimensional Rayleigh–Bénard convection.
Journal of Fluid Mechanics,
Vol. 915,
Issue. ,
Sukhanovskii, A.
and
Evgrafova, A.
2021.
Dependence of boundary layer thickness on layer height for extended localised heaters.
Experimental Thermal and Fluid Science,
Vol. 121,
Issue. ,
p.
110275.
Jeganathan, Vignesh
Alba, Kamran
and
Ostilla-Mónico, Rodolfo
2021.
Controlling secondary flows in Taylor–Couette flow using stress-free boundary conditions.
Journal of Fluid Mechanics,
Vol. 922,
Issue. ,
Vasiliev, A.
and
Sukhanovskii, A.
2021.
Turbulent convection in a cube with mixed thermal boundary conditions: low Rayleigh number regime.
International Journal of Heat and Mass Transfer,
Vol. 174,
Issue. ,
p.
121290.
Sukhanovskii, A.
and
Vasiliev, A.
2022.
Physical mechanism of the convective heat flux increasing in case of mixed boundary conditions in Rayleigh-Bénard convection.
International Journal of Heat and Mass Transfer,
Vol. 185,
Issue. ,
p.
122411.
Bassani, Francesca
Poggi, Davide
Ridolfi, Luca
and
von Hardenberg, Jost
2022.
Rayleigh-Bénard convection with thermal boundary inhomogeneities.
Physical Review E,
Vol. 105,
Issue. 2,
Vasiliev, A.Y.
Sukhanovskii, A.N.
and
Frick, P.G.
2022.
Influence of horizontal heat-insulating plates on the structure of convective flows and heat transfer in a closed cavity.
Computational Continuum Mechanics,
Vol. 15,
Issue. 1,
p.
83.
Zhao, Chao-Ben
Zhang, Yi-Zhao
Wang, Bo-Fu
Wu, Jian-Zhao
Chong, Kai Leong
and
Zhou, Quan
2022.
Modulation of turbulent Rayleigh-Bénard convection under spatially harmonic heating.
Physical Review E,
Vol. 105,
Issue. 5,
Liu, Hao-Ran
Chong, Kai Leong
Yang, Rui
Verzicco, Roberto
and
Lohse, Detlef
2022.
Turbulent Rayleigh–Bénard convection with bubbles attached to the plate.
Journal of Fluid Mechanics,
Vol. 945,
Issue. ,
Hawkins, Emily K.
Cheng, Jonathan S.
Abbate, Jewel A.
Pilegard, Timothy
Stellmach, Stephan
Julien, Keith
and
Aurnou, Jonathan M.
2023.
Laboratory Models of Planetary Core-Style Convective Turbulence.
Fluids,
Vol. 8,
Issue. 4,
p.
106.
Xia, Ke-Qing
Huang, Shi-Di
Xie, Yi-Chao
and
Zhang, Lu
2023.
Tuning heat transport via coherent structure manipulation: recent advances in thermal turbulence.
National Science Review,
Vol. 10,
Issue. 6,
Hu, Jin
Zhang, Shengqi
and
Xia, Zhenhua
2024.
Flow reversal and multiple states in turbulent Rayleigh–Bénard convection with partially isothermal plates.
Journal of Fluid Mechanics,
Vol. 987,
Issue. ,
Wang, Zhengdao
Li, Yunong
Yang, Hui
Zhang, Hua
Wei, Yikun
Qian, Yuehong
and
Zhu, Zuchao
2024.
Effects of isothermal-adiabatic boundary conditions on the transition characteristics in two-dimensional turbulent Rayleigh–Bénard convection.
Numerical Heat Transfer, Part A: Applications,
Vol. 85,
Issue. 15,
p.
2558.
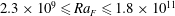 $2.3\times 10^{9}\leqslant Ra_{F}\leqslant 1.8\times 10^{11}$
and cylindrical cells in the range
$2.3\times 10^{9}\leqslant Ra_{F}\leqslant 1.8\times 10^{11}$
and cylindrical cells in the range
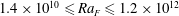 $1.4\times 10^{10}\leqslant Ra_{F}\leqslant 1.2\times 10^{12}$
with the Prandtl number
$1.4\times 10^{10}\leqslant Ra_{F}\leqslant 1.2\times 10^{12}$
with the Prandtl number
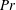 $Pr$
fixed at 4.3. It is found that the presence of the insulating lids leads to reduction of the global heat transfer efficiency as expected, which primarily depends on the insulating area but is insensitive to the detailed insulating patterns. At the leading-order level, the magnitude of temperature fluctuations in the bulk fluid is, again, found to be insensitive to the insulating pattern and mainly depends on the insulating area; while the temperature probability density function in the bulk is essentially invariant with respect to both the insulating area and the spatial pattern of the lids. The flow dynamics, on the other hand, is sensitive to both the covering area and the spatial distribution of the lids. At fixed
$Pr$
fixed at 4.3. It is found that the presence of the insulating lids leads to reduction of the global heat transfer efficiency as expected, which primarily depends on the insulating area but is insensitive to the detailed insulating patterns. At the leading-order level, the magnitude of temperature fluctuations in the bulk fluid is, again, found to be insensitive to the insulating pattern and mainly depends on the insulating area; while the temperature probability density function in the bulk is essentially invariant with respect to both the insulating area and the spatial pattern of the lids. The flow dynamics, on the other hand, is sensitive to both the covering area and the spatial distribution of the lids. At fixed
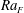 $Ra_{F}$
, the flow strength is found to increase with increasing insulating area so as to transfer the same amount of heat through a smaller cooling area. Moreover, for a constant insulating area, a symmetric insulating pattern results in a symmetric flow pattern, i.e. double-roll structure; whereas an asymmetric insulating pattern leads to asymmetric flow, i.e. single-roll structure. It is further found that the symmetry breaking of the insulating pattern leads to a stronger flow that enhances the horizontal velocity more than the vertical velocity.
$Ra_{F}$
, the flow strength is found to increase with increasing insulating area so as to transfer the same amount of heat through a smaller cooling area. Moreover, for a constant insulating area, a symmetric insulating pattern results in a symmetric flow pattern, i.e. double-roll structure; whereas an asymmetric insulating pattern leads to asymmetric flow, i.e. single-roll structure. It is further found that the symmetry breaking of the insulating pattern leads to a stronger flow that enhances the horizontal velocity more than the vertical velocity.