Published online by Cambridge University Press: 06 November 2018
High resolution large eddy simulations (LES) are performed to study the interaction of a stationary shock with fully developed turbulent flow. Turbulent statistics downstream of the interaction are provided for a range of weakly compressible upstream turbulent Mach numbers 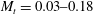 $M_{t}=0.03{-}0.18$, shock Mach numbers
$M_{t}=0.03{-}0.18$, shock Mach numbers 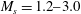 $M_{s}=1.2{-}3.0$ and Taylor-based Reynolds numbers
$M_{s}=1.2{-}3.0$ and Taylor-based Reynolds numbers 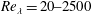 $Re_{\unicode[STIX]{x1D706}}=20{-}2500$. The LES displays minimal Reynolds number effects once an inertial range has developed for
$Re_{\unicode[STIX]{x1D706}}=20{-}2500$. The LES displays minimal Reynolds number effects once an inertial range has developed for 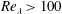 $Re_{\unicode[STIX]{x1D706}}>100$. The inertial range scales of the turbulence are shown to quickly return to isotropy, and downstream of sufficiently strong shocks this process generates a net transfer of energy from transverse into streamwise velocity fluctuations. The streamwise shock displacements are shown to approximately follow a
$Re_{\unicode[STIX]{x1D706}}>100$. The inertial range scales of the turbulence are shown to quickly return to isotropy, and downstream of sufficiently strong shocks this process generates a net transfer of energy from transverse into streamwise velocity fluctuations. The streamwise shock displacements are shown to approximately follow a 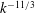 $k^{-11/3}$ decay with wavenumber as predicted by linear analysis. In conjunction with other statistics this suggests that the instantaneous interaction of the shock with the upstream turbulence proceeds in an approximately linear manner, but nonlinear effects immediately downstream of the shock significantly modify the flow even at the lowest considered turbulent Mach numbers.
$k^{-11/3}$ decay with wavenumber as predicted by linear analysis. In conjunction with other statistics this suggests that the instantaneous interaction of the shock with the upstream turbulence proceeds in an approximately linear manner, but nonlinear effects immediately downstream of the shock significantly modify the flow even at the lowest considered turbulent Mach numbers.