Published online by Cambridge University Press: 02 November 2018
Large-scale coherent structures such as jets in Rayleigh–Bénard convection and related systems are receiving increasing attention. This paper studies, both numerically and theoretically, the process of jet formation in two-dimensional salt-finger convection. The approach utilizes an asymptotically derived system of equations referred to as the modified Rayleigh–Bénard convection (MRBC) model, valid in the geophysically and astrophysically relevant limit in which the solute diffuses much more slowly than heat. In these equations, convection is driven by a destabilizing salinity gradient while the effects of the stabilizing temperature gradient manifest themselves as an additional anisotropic dissipation acting on large scales. The MRBC system is specified by two external parameters: the Schmidt number 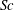 $\mathit{Sc}$ (ratio of viscosity to solutal diffusivity) and the Rayleigh ratio
$\mathit{Sc}$ (ratio of viscosity to solutal diffusivity) and the Rayleigh ratio 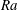 $\mathit{Ra}$ (ratio between the Rayleigh numbers of the destabilizing solutal stratification and the stabilizing thermal stratification). Two distinct
$\mathit{Ra}$ (ratio between the Rayleigh numbers of the destabilizing solutal stratification and the stabilizing thermal stratification). Two distinct 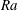 $\mathit{Ra}$ regimes are explored for fixed
$\mathit{Ra}$ regimes are explored for fixed 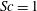 $\mathit{Sc}=1$. In all cases studied the system develops a horizontal jet structure that is maintained self-consistently by turbulent fluctuations, but coarsens over time. For intermediate Rayleigh ratios (e.g.
$\mathit{Sc}=1$. In all cases studied the system develops a horizontal jet structure that is maintained self-consistently by turbulent fluctuations, but coarsens over time. For intermediate Rayleigh ratios (e.g. 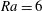 $\mathit{Ra}=6$), the MRBC model captures the relaxation oscillations superposed on the jet structure observed at similar parameter values in direct numerical simulations of the primitive equations. For smaller Rayleigh ratios (e.g.
$\mathit{Ra}=6$), the MRBC model captures the relaxation oscillations superposed on the jet structure observed at similar parameter values in direct numerical simulations of the primitive equations. For smaller Rayleigh ratios (e.g. 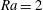 $\mathit{Ra}=2$), a regime for which direct numerical simulation of the primitive equations is difficult because of the presence of fast gravity waves, the MRBC model reveals the existence of statistically steady jets whose properties are studied in detail. Three hierarchical models, the MRBC and further reductions in the form of quasilinear and single-mode approximations, are used to confirm that jets form and are sustained as a result of the interaction between fluctuations (salt fingers) and large-scale horizontally averaged horizontal flows (jets). Even though the small-scale structures exhibited by the three models exhibit clear differences, all three produce the same power-law spectrum of the mean fields at large vertical scales: in all, the spectrum of the mean streamfunction scales as
$\mathit{Ra}=2$), a regime for which direct numerical simulation of the primitive equations is difficult because of the presence of fast gravity waves, the MRBC model reveals the existence of statistically steady jets whose properties are studied in detail. Three hierarchical models, the MRBC and further reductions in the form of quasilinear and single-mode approximations, are used to confirm that jets form and are sustained as a result of the interaction between fluctuations (salt fingers) and large-scale horizontally averaged horizontal flows (jets). Even though the small-scale structures exhibited by the three models exhibit clear differences, all three produce the same power-law spectrum of the mean fields at large vertical scales: in all, the spectrum of the mean streamfunction scales as 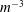 $m^{-3}$ and the mean salinity field scales as
$m^{-3}$ and the mean salinity field scales as  $m^{-1}$, with
$m^{-1}$, with  $m$ the vertical wavenumber. A theoretical explanation of these observations based on the dominant balances in the mean and fluctuation equations is provided. As a consequence, the jets have a zigzag profile, a conclusion that is consistent with numerical simulations. Based on numerical observations, a three-component phenomenological model consisting of a linearly growing mode, a linearly damped mode and a mean mode is proposed to explain the observed transition from statistically steady jet structure to jets with superposed oscillations that takes place with increasing Rayleigh ratio.
$m$ the vertical wavenumber. A theoretical explanation of these observations based on the dominant balances in the mean and fluctuation equations is provided. As a consequence, the jets have a zigzag profile, a conclusion that is consistent with numerical simulations. Based on numerical observations, a three-component phenomenological model consisting of a linearly growing mode, a linearly damped mode and a mean mode is proposed to explain the observed transition from statistically steady jet structure to jets with superposed oscillations that takes place with increasing Rayleigh ratio.