Published online by Cambridge University Press: 09 October 2019
In Crowe & Taylor (J. Fluid Mech., vol. 850, 2018, pp. 179–211) we described a theory for the evolution of density fronts in a rotating reference frame subject to strong vertical mixing using an asymptotic expansion in small Rossby number, 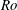 $Ro$. We found that the front reaches a balanced state where vertical diffusion is balanced by horizontal advection in the buoyancy equation. The depth-averaged buoyancy obeys a nonlinear diffusion equation which admits a similarity solution corresponding to horizontal spreading of the front. Here we use numerical simulations of the full momentum and buoyancy equations to investigate this problem for a wide range of Rossby and Ekman numbers. We examine the accuracy of our asymptotic solution and find that many aspects of the solution are valid for
$Ro$. We found that the front reaches a balanced state where vertical diffusion is balanced by horizontal advection in the buoyancy equation. The depth-averaged buoyancy obeys a nonlinear diffusion equation which admits a similarity solution corresponding to horizontal spreading of the front. Here we use numerical simulations of the full momentum and buoyancy equations to investigate this problem for a wide range of Rossby and Ekman numbers. We examine the accuracy of our asymptotic solution and find that many aspects of the solution are valid for 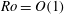 $Ro=O(1)$. However, the asymptotic solution departs from the numerical simulations for small Ekman numbers where the dominant balance in the momentum equation changes. We trace the source of this discrepancy to a depth-independent geostrophic flow that develops on both sides of the front and we develop a modification to the theory described in Crowe & Taylor (2018) to account for this geostrophic flow. The refined theory closely matches the numerical simulations, even for
$Ro=O(1)$. However, the asymptotic solution departs from the numerical simulations for small Ekman numbers where the dominant balance in the momentum equation changes. We trace the source of this discrepancy to a depth-independent geostrophic flow that develops on both sides of the front and we develop a modification to the theory described in Crowe & Taylor (2018) to account for this geostrophic flow. The refined theory closely matches the numerical simulations, even for 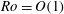 $Ro=O(1)$. Finally, we develop a new scaling for the intense vertical velocity that can develop in thin bands at the edges of the front.
$Ro=O(1)$. Finally, we develop a new scaling for the intense vertical velocity that can develop in thin bands at the edges of the front.