Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-27T20:15:40.811Z Has data issue: false hasContentIssue false
  • English
  • Français

Random walks on a dodecahedron

Published online by Cambridge University Press:  14 July 2016

G. Letac  and
L. Takács
G. Letac*
Affiliation:
Université Paul-Sabatier
L. Takács*
Affiliation:
Case Western Reserve University
*
∗Postal address: Université Paul-Sabatier, Mathématiques, 118 route de Narbonne, 31400 Toulouse, France.
∗∗Postal address: Department of Mathematics and Statistics, Case Western Reserve University, University Circle, Cleveland, OH 44106, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Abstract

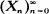We consider the general Markov chain on the vertices of a regular dodecahedron D such that P[Xn+1 = j | Xn = i] depends only on the distance between i and j. We consider also a Markov chain 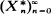on the oriented edges (i, j) of D for which the only non-zero transition probabilities are 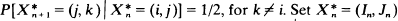and fix a vertex A. This paper computes explicitly P[Xn = A | X0 = A] and P[In = A | I0 = A]. The methods used are applicable to other solids.

Keywords

MARKOV CHAINSREGULAR DODECAHEDRON
Type
Research Papers
Information
Journal of Applied Probability , Volume 17 , Issue 2 , June 1980 , pp. 373 - 384
Copyright
Copyright © Applied Probability Trust 1980 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The paper was prepared while this author was in residence at Case Western Reserve University as Visiting Professor of Mathematics and Statistics.

References

[1] Arnaud, J. P. (1977) Sur quelques propriétés des librairies. Thèse 3eme cycle, Université Paul-Sabatier, Toulouse.Google Scholar
[2] Callahan, F. P. (1966) Problem E1897. Amer. Math. Monthly 73, 665. Solution by Kuttler, J. R. and Rubenstein, N., Amer. Math. Monthly 74 (1977), 1008–1010.Google Scholar
[3] Engel, A. (1965) Problem E1752. Amer. Math. Monthly 72, 75. Solution by Teichmann, T., Amer. Math. Monthly 73 (1966), 200.Google Scholar
[4] Heller, A. (1965) On stochastic processes derived from Markov chains. Ann. Math. Statist. 36, 1286–1291.Google Scholar
[5] Letac, G. (1977) Problem 6149. Amer. Math. Monthly 84, 301.Google Scholar
[6] Letac, G. (1978) Chaînes de Markov sur les permutations. Presses de l'Universite de Montréal, Montréal.Google Scholar