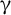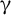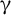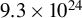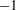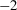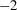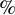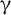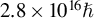1. Introduction
The rapid development of laser technologies promises substantial growth of peak laser intensities and thus has pushed laser–plasma interaction to the relativistic regime over the past several decades[
Reference Mourou, Tajima and Bulanov1]. This has provided opportunities for building tabletop particle accelerators and compact X/
![]() $\gamma$
-ray radiation sources[
Reference Mourou, Tajima and Bulanov1–
Reference Cipiccia, Islam, Ersfeld, Shanks, Brunetti, Vieux, Yang, Issac, Wiggins, Welsh, Anania, Maneuski, Montgomery, Smith, Hoek, Hamilton, Lemos, Symes, Rajeev, Shea, Dias and Jaroszynski7]. Brilliant
$\gamma$
-ray radiation sources[
Reference Mourou, Tajima and Bulanov1–
Reference Cipiccia, Islam, Ersfeld, Shanks, Brunetti, Vieux, Yang, Issac, Wiggins, Welsh, Anania, Maneuski, Montgomery, Smith, Hoek, Hamilton, Lemos, Symes, Rajeev, Shea, Dias and Jaroszynski7]. Brilliant
![]() $\gamma$
-rays in the multi-MeV regime play an important role in fundamental science and practical applications, such as nuclear physics, astrophysics, radiography of dense objects and diagnosis for laser–plasma interactions[
Reference Schwoerer, Magill and Beleites8–
Reference Yu, Liu, Zhao, Zhu, Lu, Cao, Zhang, Shao and Sheng15]. In particular, ultrashort multi-MeV
$\gamma$
-rays in the multi-MeV regime play an important role in fundamental science and practical applications, such as nuclear physics, astrophysics, radiography of dense objects and diagnosis for laser–plasma interactions[
Reference Schwoerer, Magill and Beleites8–
Reference Yu, Liu, Zhao, Zhu, Lu, Cao, Zhang, Shao and Sheng15]. In particular, ultrashort multi-MeV
![]() $\gamma$
-rays with beam angular momentum (BAM) are likely to be indispensable for time-resolved nuclear spectroscopy[
Reference Li, Hatsagortsyan, Galow and Keitel16] and nuclear resonance fluorescence, since the reaction cross-sections depend on the angular momentum of incoming multi-MeV
$\gamma$
-rays with beam angular momentum (BAM) are likely to be indispensable for time-resolved nuclear spectroscopy[
Reference Li, Hatsagortsyan, Galow and Keitel16] and nuclear resonance fluorescence, since the reaction cross-sections depend on the angular momentum of incoming multi-MeV
![]() $\gamma$
-rays due to the conservation laws of angular momentum[
Reference Taira, Hayakawa and Katoh17].
$\gamma$
-rays due to the conservation laws of angular momentum[
Reference Taira, Hayakawa and Katoh17].
In order to obtain brilliant ultrashort X/
![]() $\gamma$
-rays with BAM, numerous schemes have been recently proposed based on various radiation mechanisms, such as relativistic high-order harmonics, X-ray free-electron lasers and Thomson/Compton backscattering[
Reference Zhu, Chen, Yu, Weng, Hu, McKenna and Sheng18–
Reference Huang and Deng26]. For example, relativistic high-order harmonics with orbital angular momentum (OAM) can be obtained via collective electron oscillations by imprinting a relativistic laser pulse on a solid interface[
Reference Zhang, Shen, Shi, Wang, Zhang, Wang, Xu, Yi and Xu21,
Reference Wang, Zepf and Rykovanov24]. It is also shown that fully coherent hard X-ray OAM beams can be generated straightforwardly via mode selection in an X-ray free-electron laser oscillator configuration[
Reference Huang and Deng26]. Meanwhile, high-energy X/
$\gamma$
-rays with BAM, numerous schemes have been recently proposed based on various radiation mechanisms, such as relativistic high-order harmonics, X-ray free-electron lasers and Thomson/Compton backscattering[
Reference Zhu, Chen, Yu, Weng, Hu, McKenna and Sheng18–
Reference Huang and Deng26]. For example, relativistic high-order harmonics with orbital angular momentum (OAM) can be obtained via collective electron oscillations by imprinting a relativistic laser pulse on a solid interface[
Reference Zhang, Shen, Shi, Wang, Zhang, Wang, Xu, Yi and Xu21,
Reference Wang, Zepf and Rykovanov24]. It is also shown that fully coherent hard X-ray OAM beams can be generated straightforwardly via mode selection in an X-ray free-electron laser oscillator configuration[
Reference Huang and Deng26]. Meanwhile, high-energy X/
![]() $\gamma$
-rays with BAM can also be generated by Thomson/Compton scattering of an intense laser pulse off a counter-propagating relativistic electron beam[
Reference Bulanov, Esirkepov and Tajima27–
Reference Yan, Fruhling, Golovin, Haden, Luo, Zhang, Zhao, Zhang, Liu, Chen, Chen, Banerjee and Umstadter31]. However, the radiation sources achieved above have limitations, including the photon energy, brilliance, divergence and duration. In particular, it is very challenging to produce ultra-brilliant attosecond (as)
$\gamma$
-rays with BAM can also be generated by Thomson/Compton scattering of an intense laser pulse off a counter-propagating relativistic electron beam[
Reference Bulanov, Esirkepov and Tajima27–
Reference Yan, Fruhling, Golovin, Haden, Luo, Zhang, Zhao, Zhang, Liu, Chen, Chen, Banerjee and Umstadter31]. However, the radiation sources achieved above have limitations, including the photon energy, brilliance, divergence and duration. In particular, it is very challenging to produce ultra-brilliant attosecond (as)
![]() $\gamma$
-rays in the multi-MeV regime.
$\gamma$
-rays in the multi-MeV regime.
Recently, the vortex laser has been extensively investigated, which opens a new degree of freedom for laser–plasma interaction. A Laguerre–Gaussian laser pulse at relativistic intensities possesses high OAM density and hollow laser fields[
Reference Allen, Beijersbergen, Spreeuw and Woerdman32–
Reference Haines36], making it interesting for many potential applications, such as charged particle acceleration[
Reference Vieira and Mendonca37–
Reference Zhang, Hu, Cao, Shao and Yu44], extreme magnetic field generation[
Reference Shi, Vieira, Trines, Bingham, Shen and Kingham45,
Reference Wu and Wang46] and X/
![]() $\gamma$
-ray radiation sources[
Reference Zhu, Chen, Yu, Weng, Hu, McKenna and Sheng18–
Reference Wang, Zepf and Rykovanov24]. In this paper, we propose an all-optical scheme to generate high-brilliance isolated attosecond
$\gamma$
-ray radiation sources[
Reference Zhu, Chen, Yu, Weng, Hu, McKenna and Sheng18–
Reference Wang, Zepf and Rykovanov24]. In this paper, we propose an all-optical scheme to generate high-brilliance isolated attosecond
![]() $\gamma$
-rays with laser parameters attainable in the near future. In the scheme, a rotating relativistic electron sheet with large BAM is firstly generated and accelerated by irradiating a few-cycle twisted laser pulse onto a micro-droplet target. Then the relativistic electron sheet collides head-on with a counter-propagating Gaussian laser pulse, resulting in a copious number of
$\gamma$
-rays with laser parameters attainable in the near future. In the scheme, a rotating relativistic electron sheet with large BAM is firstly generated and accelerated by irradiating a few-cycle twisted laser pulse onto a micro-droplet target. Then the relativistic electron sheet collides head-on with a counter-propagating Gaussian laser pulse, resulting in a copious number of
![]() $\gamma$
-photons being emitted. Three-dimensional particle-in-cell (3D-PIC) simulations demonstrate that the electron sheet can transfer about
$\gamma$
-photons being emitted. Three-dimensional particle-in-cell (3D-PIC) simulations demonstrate that the electron sheet can transfer about
![]() $9.8\%$
energy and
$9.8\%$
energy and
![]() $9.4\%$
angular momentum simultaneously to the photons. The
$9.4\%$
angular momentum simultaneously to the photons. The
![]() $\gamma$
-rays are characterized by a duration as short as 320 as, BAM of
$\gamma$
-rays are characterized by a duration as short as 320 as, BAM of
![]() $2.8\times {10}^{16}\mathrm{\hslash}$
and peak brilliance of 9.3×1024 photons s
$2.8\times {10}^{16}\mathrm{\hslash}$
and peak brilliance of 9.3×1024 photons s
![]() ${}^{-1}$
mrad
${}^{-1}$
mrad
![]() ${}^{-2}$
mm
${}^{-2}$
mm
![]() ${}^{-2}$
per 0.1
${}^{-2}$
per 0.1
![]() $\%$
bandwidth at 4.3 MeV.
$\%$
bandwidth at 4.3 MeV.
To the best of our knowledge, high-quality isolated attosecond electron bunches are crucial for the production of ultra-brilliant isolated attosecond
![]() $\gamma$
-rays via nonlinear Thomson scattering. In previous works, various schemes have been proposed for generating dense attosecond electron bunches with low divergence and high beam charge, but it is still a great challenge to produce an isolated attosecond electron bunch. For example, we propose an all-optical scheme for generating dense attosecond electron bunches via the interaction of an intense Laguerre–Gaussian laser pulse with a nanofiber or droplet target[
Reference Hu, Yu, Sheng, Vieira, Zou, Yin, McKenna and Shao47,
Reference Hu, Yu, Li, Yin, McKenna and Shao48]. However, the produced beam consists of a series of attosecond electron bunches. Wu et al. [
Reference Wu, Meyer-ter-Vehn, Fernandez and Hegelich49] proposed to generate uniform relativistic electron layers from an ultrathin solid foil. However, the electron density and charge are very low. Lin et al. [
Reference Lin, Batson, Nees, Thomas and Krushelnick50] also proposed to produce isolated attosecond electron bunches with single-cycle Gaussian pulses or tilted laser pulses. However, the quality of the generated electron bunches is poor.
$\gamma$
-rays via nonlinear Thomson scattering. In previous works, various schemes have been proposed for generating dense attosecond electron bunches with low divergence and high beam charge, but it is still a great challenge to produce an isolated attosecond electron bunch. For example, we propose an all-optical scheme for generating dense attosecond electron bunches via the interaction of an intense Laguerre–Gaussian laser pulse with a nanofiber or droplet target[
Reference Hu, Yu, Sheng, Vieira, Zou, Yin, McKenna and Shao47,
Reference Hu, Yu, Li, Yin, McKenna and Shao48]. However, the produced beam consists of a series of attosecond electron bunches. Wu et al. [
Reference Wu, Meyer-ter-Vehn, Fernandez and Hegelich49] proposed to generate uniform relativistic electron layers from an ultrathin solid foil. However, the electron density and charge are very low. Lin et al. [
Reference Lin, Batson, Nees, Thomas and Krushelnick50] also proposed to produce isolated attosecond electron bunches with single-cycle Gaussian pulses or tilted laser pulses. However, the quality of the generated electron bunches is poor.
2. Simulation setup and results
Here we schematically show the isolated attosecond
![]() $\gamma$
-ray emission from a twisted drive laser interaction with a micro-droplet in Figure 1(a). In this scheme, the drive laser behaves like a vortex saw, which cuts the droplet and generates the relativistic electron sheet. The 3D-PIC code EPOCH has been employed, which incorporates a quantum electrodynamics module and quantum-corrected photon emission modules[
Reference Ridgers, Kirk, Duclous, Blackburn, Brady, Bennett, Arber and Bell51,
Reference Arber, Bennett, Brady, Lawrence-Douglas, Ramsay, Sircombe, Gillies, Evans, Schmitz and Bell52]. The size of the simulation box is
$\gamma$
-ray emission from a twisted drive laser interaction with a micro-droplet in Figure 1(a). In this scheme, the drive laser behaves like a vortex saw, which cuts the droplet and generates the relativistic electron sheet. The 3D-PIC code EPOCH has been employed, which incorporates a quantum electrodynamics module and quantum-corrected photon emission modules[
Reference Ridgers, Kirk, Duclous, Blackburn, Brady, Bennett, Arber and Bell51,
Reference Arber, Bennett, Brady, Lawrence-Douglas, Ramsay, Sircombe, Gillies, Evans, Schmitz and Bell52]. The size of the simulation box is
![]() $x\times y\times z=48{\lambda}_0\times 12{\lambda}_0\times 12{\lambda}_0$
with each cell being of 0.02
$x\times y\times z=48{\lambda}_0\times 12{\lambda}_0\times 12{\lambda}_0$
with each cell being of 0.02
![]() ${\lambda}_0\times 0.02{\lambda}_0\times 0.02{\lambda}_0$
. The time step is automatically chosen in the simulations to guarantee numerical stability. Absorbing boundary conditions for the fields and particles are applied both in
${\lambda}_0\times 0.02{\lambda}_0\times 0.02{\lambda}_0$
. The time step is automatically chosen in the simulations to guarantee numerical stability. Absorbing boundary conditions for the fields and particles are applied both in
![]() $y$
and
$y$
and
![]() $z$
directions. Each cell contains
$z$
directions. Each cell contains
![]() $64$
macro-electrons and
$64$
macro-electrons and
![]() $64$
macro-ions in the initial plasma zone. A pre-ionized helium micro-droplet target with a radius of
$64$
macro-ions in the initial plasma zone. A pre-ionized helium micro-droplet target with a radius of
![]() ${\lambda}_0$
and density of 10
${\lambda}_0$
and density of 10
![]() ${n}_{\mathrm{c}}$
is located at
${n}_{\mathrm{c}}$
is located at
![]() $\left(4{\lambda}_0,0,0\right)$
, where
$\left(4{\lambda}_0,0,0\right)$
, where
![]() ${n}_{\mathrm{c}}=1.12\times {10}^{21}$
cm
${n}_{\mathrm{c}}=1.12\times {10}^{21}$
cm
![]() ${}^{-3}$
is the critical density for a
${}^{-3}$
is the critical density for a
![]() ${\lambda}_0=1\;\mu \mathrm{m}$
drive laser pulse. It is shown that the main simulation results remain unchanged when
${\lambda}_0=1\;\mu \mathrm{m}$
drive laser pulse. It is shown that the main simulation results remain unchanged when
![]() ${\lambda}_0=0.8\ \mu \mathrm{m}$
or the initial electron density is set to 50
${\lambda}_0=0.8\ \mu \mathrm{m}$
or the initial electron density is set to 50
![]() ${n}_{\mathrm{c}}$
(see Figure S4 in the Supplementary Material). These types of targets with different density could be generated by the standard droplet system. A left-handed circularly polarized Laguerre–Gaussian laser pulse with mode (1, 0) propagates along the x-axis and is focused at the droplet target with
${n}_{\mathrm{c}}$
(see Figure S4 in the Supplementary Material). These types of targets with different density could be generated by the standard droplet system. A left-handed circularly polarized Laguerre–Gaussian laser pulse with mode (1, 0) propagates along the x-axis and is focused at the droplet target with
 $\overrightarrow{a}=\sqrt{2e}{a}_0r{\sigma}_0{\sigma}^{-2}\exp \left(-{r}^2/{\sigma}^2\right){\sin}^2\left[\pi \left(x- ct\right)/2\tau \right]\times \left(\sin \Psi {\overrightarrow{e}}_y-\cos \Psi {\overrightarrow{e}}_z\right),$
where
$\overrightarrow{a}=\sqrt{2e}{a}_0r{\sigma}_0{\sigma}^{-2}\exp \left(-{r}^2/{\sigma}^2\right){\sin}^2\left[\pi \left(x- ct\right)/2\tau \right]\times \left(\sin \Psi {\overrightarrow{e}}_y-\cos \Psi {\overrightarrow{e}}_z\right),$
where
![]() ${a}_0=45$
is the dimensionless peak amplitude,
${a}_0=45$
is the dimensionless peak amplitude,
![]() $\sigma ={\sigma}_0\sqrt{1+{x}^2/{R}_{\mathrm{L}}^2}$
,
$\sigma ={\sigma}_0\sqrt{1+{x}^2/{R}_{\mathrm{L}}^2}$
,
![]() ${\sigma}_0=$
3.5
${\sigma}_0=$
3.5
![]() ${\lambda}_0$
is the beam waist radius,
${\lambda}_0$
is the beam waist radius,
![]() ${R}_{\mathrm{L}}$
is the Rayleigh length,
${R}_{\mathrm{L}}$
is the Rayleigh length,
![]() $\Psi ={\omega}_0t-{k}_0\left(x+{r}^2/2{R}_{\mathrm{C}}\right)-2\arctan \left(x/{R}_{\mathrm{L}}\right)+\varphi +{\psi}_0$
,
$\Psi ={\omega}_0t-{k}_0\left(x+{r}^2/2{R}_{\mathrm{C}}\right)-2\arctan \left(x/{R}_{\mathrm{L}}\right)+\varphi +{\psi}_0$
,
![]() ${R}_{\mathrm{C}}$
is the curvature radius of the wave-front and
${R}_{\mathrm{C}}$
is the curvature radius of the wave-front and
![]() $\varphi$
denotes the azimuthal angle. To generate a single attosecond electron sheet, we set initially the pulse duration
$\varphi$
denotes the azimuthal angle. To generate a single attosecond electron sheet, we set initially the pulse duration
![]() $2\tau =3{T}_0$
and the carrier-envelope phase (CEP)
$2\tau =3{T}_0$
and the carrier-envelope phase (CEP)
![]() ${\psi}_0=3\pi /2$
, where
${\psi}_0=3\pi /2$
, where
![]() ${T}_0$
is the laser cycle. Currently, it is challenging to generate such a CEP stabilized, few-cycle twisted laser pulse. In experiments, a relativistic vortex laser with the intensity of
${T}_0$
is the laser cycle. Currently, it is challenging to generate such a CEP stabilized, few-cycle twisted laser pulse. In experiments, a relativistic vortex laser with the intensity of
![]() $6.3\times {10}^{19}$
W/cm
$6.3\times {10}^{19}$
W/cm
![]() ${}^2$
has been generated[
Reference Wang, Jiang, Dong, Lu, Li, Xu, Sun, Yu, Guo, Liang, Leng, Li and Xu39]. Ultra-broadband gold gratings for near-single-cycle 100-PW laser pulse stretching and compression were also realized[
Reference Han, Li, Zhang, Kong, Cao, Jin, Leng, Li and Shao53]. One possible method to obtain the demanded few-cycle laser pulse is utilizing the gold gratings to post-compress a twisted laser pulse in the near future.
${}^2$
has been generated[
Reference Wang, Jiang, Dong, Lu, Li, Xu, Sun, Yu, Guo, Liang, Leng, Li and Xu39]. Ultra-broadband gold gratings for near-single-cycle 100-PW laser pulse stretching and compression were also realized[
Reference Han, Li, Zhang, Kong, Cao, Jin, Leng, Li and Shao53]. One possible method to obtain the demanded few-cycle laser pulse is utilizing the gold gratings to post-compress a twisted laser pulse in the near future.

Figure 1 (a) Schematic diagram of an intense Laguerre–Gaussian laser pulse interaction with a micro-droplet target. Here, the map in the
![]() $xoy$
plane presents the projection of electron density and the red curve in the
$xoy$
plane presents the projection of electron density and the red curve in the
![]() $xoz$
plane shows the photon density distribution along the laser axis. The U-shaped red arrow shows the scattering process of a counterstreaming linearly polarized Gaussian laser pulse off a rotating relativistic electron sheet. (b) Transverse electron density distribution at
$xoz$
plane shows the photon density distribution along the laser axis. The U-shaped red arrow shows the scattering process of a counterstreaming linearly polarized Gaussian laser pulse off a rotating relativistic electron sheet. (b) Transverse electron density distribution at
![]() $t=10{T}_0$
, 20
$t=10{T}_0$
, 20
![]() ${T}_0$
and 30
${T}_0$
and 30
![]() ${T}_0$
, respectively. (c), (d) Electron divergence angle at
${T}_0$
, respectively. (c), (d) Electron divergence angle at
![]() $t=30{T}_0$
and evolution of the electron energy spectrum. (e), (f) Electron distribution in the phase space
$t=30{T}_0$
and evolution of the electron energy spectrum. (e), (f) Electron distribution in the phase space
![]() $\left({\beta}_x,{\beta}_y\right)$
and
$\left({\beta}_x,{\beta}_y\right)$
and
![]() $\left({p}_x,\gamma \right)$
at
$\left({p}_x,\gamma \right)$
at
![]() $t=10{T}_0$
. Here, the magenta arrows in (b) denote the average transverse momentum of electrons at each cell. The red curves in (e) and (f) represent electron numbers with respect to the longitudinal velocity
$t=10{T}_0$
. Here, the magenta arrows in (b) denote the average transverse momentum of electrons at each cell. The red curves in (e) and (f) represent electron numbers with respect to the longitudinal velocity
![]() ${\beta}_x$
and dephasing rate
${\beta}_x$
and dephasing rate
![]() $R$
, respectively.
$R$
, respectively.
2.1. The generation of rotating attosecond electron sheets
When an intense circularly polarized Laguerre–Gaussian laser pulse illuminates the droplet, abundant electrons are dragged out of the droplet, forming an isolated dense electron layer, as shown in Figure 1(b). The electron layer has a maximal density of
![]() $15{n}_{\mathrm{c}}$
and a duration of 330 as at
$15{n}_{\mathrm{c}}$
and a duration of 330 as at
![]() $t=10{T}_0$
. As the electron layer co-moves with the laser pulse, it is continuously compressed along the longitudinal direction with the duration decreasing to 200 as at
$t=10{T}_0$
. As the electron layer co-moves with the laser pulse, it is continuously compressed along the longitudinal direction with the duration decreasing to 200 as at
![]() $t=30{T}_0$
. Meanwhile, more and more electrons counterclockwise rotate around the optics axis over time. We can also observe the signature of rotation of the relativistic electron sheet from the projection of three-dimensional (3D) electron trajectories in the
$t=30{T}_0$
. Meanwhile, more and more electrons counterclockwise rotate around the optics axis over time. We can also observe the signature of rotation of the relativistic electron sheet from the projection of three-dimensional (3D) electron trajectories in the
![]() $yoz$
plane (see Figure S1(a) in the Supplementary Material). These electrons are simultaneously confined by the transverse ponderomotive force,
$yoz$
plane (see Figure S1(a) in the Supplementary Material). These electrons are simultaneously confined by the transverse ponderomotive force,
 ${F}_{\mathrm{tr}}=\sqrt{2e}{a}_0{m}_{\mathrm{e}0}{\omega}_0c\left(2{r}^2/{\sigma}^2-1\right){\sigma}_0{\left(k{\sigma}^2\right)}^{-1}\exp \left(-{r}^2/{\sigma}^2\right)\cdot {\sin}^2\left[\pi \left(x- ct\right)/2\tau \right]$
, which points to the optical axis and thus pushes the electrons to the center. Here,
${F}_{\mathrm{tr}}=\sqrt{2e}{a}_0{m}_{\mathrm{e}0}{\omega}_0c\left(2{r}^2/{\sigma}^2-1\right){\sigma}_0{\left(k{\sigma}^2\right)}^{-1}\exp \left(-{r}^2/{\sigma}^2\right)\cdot {\sin}^2\left[\pi \left(x- ct\right)/2\tau \right]$
, which points to the optical axis and thus pushes the electrons to the center. Here,
![]() ${m}_{\mathrm{e}0}$
denotes the electron rest mass and
${m}_{\mathrm{e}0}$
denotes the electron rest mass and
![]() $c$
is the speed of light in vacuum. This finally leads to a small electron divergence angle of approximately
$c$
is the speed of light in vacuum. This finally leads to a small electron divergence angle of approximately
![]() ${2}^{\circ }$
at
${2}^{\circ }$
at
![]() $t=30{T}_0$
, as seen in Figure 1(c). During this process, not only is an isolated attosecond electron sheet generated, but also its density is greatly increased[
Reference Bulanov, Esirkepov and Tajima27,
Reference Luttikhof, Khachatryan, van Goor and Boller54,
Reference Ferri, Horný and Fülöp55] and the beam divergence is decreased[
Reference Kulagin, Cherepenin, Hur and Suk56]. It is important for the droplet target to align with the laser pulse. To generate a dense isolated attosecond electron sheet, the droplet target should be located in the focal spot, namely in the region of
$t=30{T}_0$
, as seen in Figure 1(c). During this process, not only is an isolated attosecond electron sheet generated, but also its density is greatly increased[
Reference Bulanov, Esirkepov and Tajima27,
Reference Luttikhof, Khachatryan, van Goor and Boller54,
Reference Ferri, Horný and Fülöp55] and the beam divergence is decreased[
Reference Kulagin, Cherepenin, Hur and Suk56]. It is important for the droplet target to align with the laser pulse. To generate a dense isolated attosecond electron sheet, the droplet target should be located in the focal spot, namely in the region of
![]() $r<{\sigma}_0/\sqrt{2}$
. Since the droplet target is spherical, the transverse misalignments of the sphere center may affect the results. Therefore, the transverse misalignments should be precisely controlled in experiments with sensing and a control scheme of positions[
Reference Mizoguchi, Tomuro, Nishimura, Hosoda, Nakarai, Abe, Tanaka, Watanabe, Shiraishi, Yanagiga, Soumagne, Iwamoto, Nagai, Ueno, Suganuma, Niimi, Yabu, Yamada and Saitou57].
$r<{\sigma}_0/\sqrt{2}$
. Since the droplet target is spherical, the transverse misalignments of the sphere center may affect the results. Therefore, the transverse misalignments should be precisely controlled in experiments with sensing and a control scheme of positions[
Reference Mizoguchi, Tomuro, Nishimura, Hosoda, Nakarai, Abe, Tanaka, Watanabe, Shiraishi, Yanagiga, Soumagne, Iwamoto, Nagai, Ueno, Suganuma, Niimi, Yabu, Yamada and Saitou57].
It is interesting to see that this isolated electron bunch shows an initial quasi-monoenergetic distribution, as shown in Figure 1(d), whose cut-off energy is up to 340 MeV at
![]() $t=30{T}_0$
. Figure 1(e) illuminates the electron distribution in the phase space
$t=30{T}_0$
. Figure 1(e) illuminates the electron distribution in the phase space
![]() $\left({\beta}_x,{\beta}_y\right)$
, which shows that most electrons are located within the zone
$\left({\beta}_x,{\beta}_y\right)$
, which shows that most electrons are located within the zone
![]() ${\beta}_x\approx 1$
. The red curve indicates that the longitudinal velocity
${\beta}_x\approx 1$
. The red curve indicates that the longitudinal velocity
![]() ${\beta}_x$
of more than 50
${\beta}_x$
of more than 50
![]() $\%$
of electrons is larger than 0.998. Figure 1(f) presents the electron distribution in the phase space
$\%$
of electrons is larger than 0.998. Figure 1(f) presents the electron distribution in the phase space
![]() $\left({p}_x,\gamma \right)$
. Here, one sees that
$\left({p}_x,\gamma \right)$
. Here, one sees that
![]() $\gamma =\sqrt{1+{p}^2}\approx {p}_x$
. Meanwhile, the dephasing rate[
Reference Robinson, Arefiev and Neely58]
$\gamma =\sqrt{1+{p}^2}\approx {p}_x$
. Meanwhile, the dephasing rate[
Reference Robinson, Arefiev and Neely58]
![]() $R=\gamma -{p}_x=1+\left({q}_{\mathrm{e}}/{m}_{\mathrm{e}0}c\right)\int {E}_x\mathrm{d}\tau <0.125$
for more than 50
$R=\gamma -{p}_x=1+\left({q}_{\mathrm{e}}/{m}_{\mathrm{e}0}c\right)\int {E}_x\mathrm{d}\tau <0.125$
for more than 50
![]() $\%$
of the electrons. These electrons co-move forward at a velocity close to
$\%$
of the electrons. These electrons co-move forward at a velocity close to
![]() $c$
and are phase-locked swiftly by the laser in the longitudinal direction. Since the laser magnetic force counteracts the laser radial electric force, the electrons are subject to null force in the transverse direction, so that the electron layer keeps the intact structure during the propagation. This plays a critical role for bright
$c$
and are phase-locked swiftly by the laser in the longitudinal direction. Since the laser magnetic force counteracts the laser radial electric force, the electrons are subject to null force in the transverse direction, so that the electron layer keeps the intact structure during the propagation. This plays a critical role for bright
![]() $\gamma$
-ray emission in the subsequent processes.
$\gamma$
-ray emission in the subsequent processes.

Figure 2 (a) Normalized longitudinal electric field
![]() ${a}_x$
and (b) Q factor with respect to
${a}_x$
and (b) Q factor with respect to
![]() $\Delta \psi =\psi -{\psi}_0$
. The red, black, blue and green curves correspond to the cases of CEP
$\Delta \psi =\psi -{\psi}_0$
. The red, black, blue and green curves correspond to the cases of CEP
![]() $=0$
,
$=0$
,
![]() $\pi /2$
,
$\pi /2$
,
![]() $\pi$
and
$\pi$
and
![]() $3\pi /2$
, respectively. Evolution of
$3\pi /2$
, respectively. Evolution of
![]() ${\beta}_x$
with respect to
${\beta}_x$
with respect to
![]() $\psi -{\psi}_0$
when the CEP equals (c)
$\psi -{\psi}_0$
when the CEP equals (c)
![]() $0$
, (d)
$0$
, (d)
![]() $\pi /2$
, (e)
$\pi /2$
, (e)
![]() $\pi$
and (f)
$\pi$
and (f)
![]() $3\pi /2$
in the case of
$3\pi /2$
in the case of
![]() ${a}_{x0}=0.2$
(dashed) and
${a}_{x0}=0.2$
(dashed) and
![]() $0.998$
(solid), respectively.
$0.998$
(solid), respectively.
Since only electrons phase-locked simultaneously in the transverse and longitudinal directions are able to be accelerated continuously in the laser field, we may achieve an isolated short electron bunch by manipulating electron phase-locking. Since the laser magnetic force counteracts the laser radial electric force in the transverse direction, electrons can be tightly confined around the laser axis. The transverse velocity of electrons is much less than the longitudinal velocity, as shown in Figure 1(e). Therefore, we ignore the transverse electron motion in the following analysis, which agrees with our particle-in-cell (PIC) simulation results. The electrons’ motion in one-dimensional approximation can be described by
![]() $\mathrm{d}{p}_x/\mathrm{d}t=-{q}_{\mathrm{e}}{E}_x$
and
$\mathrm{d}{p}_x/\mathrm{d}t=-{q}_{\mathrm{e}}{E}_x$
and
![]() $d\left(\gamma {m}_{\mathrm{e}0}{c}^2\right)/\mathrm{d}t=-{q}_{\mathrm{e}}{v}_x{E}_x$
. We have
$d\left(\gamma {m}_{\mathrm{e}0}{c}^2\right)/\mathrm{d}t=-{q}_{\mathrm{e}}{v}_x{E}_x$
. We have
![]() ${a}_x={q}_{\mathrm{e}}{E}_x/{m}_{\mathrm{e}0}{\omega}_0c=-{a}_{x0}{\sin}^2\left[\pi \left(x- ct\right)/2\tau \right]\cos \psi$
, where
${a}_x={q}_{\mathrm{e}}{E}_x/{m}_{\mathrm{e}0}{\omega}_0c=-{a}_{x0}{\sin}^2\left[\pi \left(x- ct\right)/2\tau \right]\cos \psi$
, where
![]() ${a}_{x0}=2\sqrt{2e}{a}_0/{k}_0{\sigma}_0$
and
${a}_{x0}=2\sqrt{2e}{a}_0/{k}_0{\sigma}_0$
and
![]() $\psi ={\omega}_0t-{k}_0x+{\psi}_0$
. For a short laser pulse,
$\psi ={\omega}_0t-{k}_0x+{\psi}_0$
. For a short laser pulse,
![]() ${a}_x$
depends sensitively on the CEP, as shown in Figure 2(a). Here, the longitudinal velocity of electrons can be derived from the equations above:
${a}_x$
depends sensitively on the CEP, as shown in Figure 2(a). Here, the longitudinal velocity of electrons can be derived from the equations above:
 $$\begin{align}{\beta}_x=\frac{1-{\left(1-{a}_{x0}Q\right)}^2}{1+{\left(1-{a}_{x0}Q\right)}^2},\end{align}$$
$$\begin{align}{\beta}_x=\frac{1-{\left(1-{a}_{x0}Q\right)}^2}{1+{\left(1-{a}_{x0}Q\right)}^2},\end{align}$$
where the factor
 $Q=\left(1/2\right)\sin \psi -\left[\tau /\left(4\tau -2\right)\right]\sin [\left(2\tau -1\right)\cdot \psi /2\tau +{\psi}_0/2\tau ]-\left[\tau /\left(4\tau +2\right)\right]\sin [\left(2\tau +1\right)\psi /2\tau -{\psi}_0/ 2\tau ]+\left[1/\left(8{\tau}^2-2\right)\right]\sin {\psi}_0$
. The
$Q=\left(1/2\right)\sin \psi -\left[\tau /\left(4\tau -2\right)\right]\sin [\left(2\tau -1\right)\cdot \psi /2\tau +{\psi}_0/2\tau ]-\left[\tau /\left(4\tau +2\right)\right]\sin [\left(2\tau +1\right)\psi /2\tau -{\psi}_0/ 2\tau ]+\left[1/\left(8{\tau}^2-2\right)\right]\sin {\psi}_0$
. The
![]() $Q$
factor always ranges from −1 to 1 for different
$Q$
factor always ranges from −1 to 1 for different
![]() ${\psi}_0$
, as shown in Figure 2(b). We can derive the local maximum nodes
${\psi}_0$
, as shown in Figure 2(b). We can derive the local maximum nodes
![]() ${\psi}_{\mathrm{max}}=2 k\pi +\pi /2$
from the equation
${\psi}_{\mathrm{max}}=2 k\pi +\pi /2$
from the equation
![]() $\mathrm{d}{\beta}_x/\mathrm{d}\psi =0$
, where
$\mathrm{d}{\beta}_x/\mathrm{d}\psi =0$
, where
![]() $k=0,\pm 1,\pm 2,\cdots$
. Here,
$k=0,\pm 1,\pm 2,\cdots$
. Here,
![]() $k=0,\, 1,\, 2$
when the pulse duration
$k=0,\, 1,\, 2$
when the pulse duration
![]() $2\tau =3{T}_0$
. Obviously, only when
$2\tau =3{T}_0$
. Obviously, only when
![]() $k=2$
and the CEP
$k=2$
and the CEP
![]() ${\psi}_0=3\pi /2$
, namely
${\psi}_0=3\pi /2$
, namely
![]() $\psi ={\psi}_{\mathrm{max}}=9\pi /2$
and
$\psi ={\psi}_{\mathrm{max}}=9\pi /2$
and
![]() $\Delta \psi =\psi -{\psi}_0=3\pi$
,
$\Delta \psi =\psi -{\psi}_0=3\pi$
,
![]() $Q=1$
and
$Q=1$
and
![]() ${\beta}_x$
reaches the peak
${\beta}_x$
reaches the peak
![]() ${\beta}_{x, \mathrm{peak}}=\left[1-{\left(1-{a}_{x0}\right)}^2\right]/\left[1+{\left(1-{a}_{x0}\right)}^2\right]$
. When we set a longer pulse duration, the number of local maximum nodes will increase. The CEP
${\beta}_{x, \mathrm{peak}}=\left[1-{\left(1-{a}_{x0}\right)}^2\right]/\left[1+{\left(1-{a}_{x0}\right)}^2\right]$
. When we set a longer pulse duration, the number of local maximum nodes will increase. The CEP
![]() ${\psi}_0$
for the peak of
${\psi}_0$
for the peak of
![]() ${\beta}_x$
also alters. To phase-lock electrons,
${\beta}_x$
also alters. To phase-lock electrons,
![]() ${\beta}_{x,\mathit{\max}}=1$
should be satisfied and we obtain
${\beta}_{x,\mathit{\max}}=1$
should be satisfied and we obtain
![]() ${a}_{x0}=1$
. Actually, considering the influence of Guoy phase and focal spot variation,
${a}_{x0}=1$
. Actually, considering the influence of Guoy phase and focal spot variation,
![]() ${\beta}_{x, \mathrm{peak}}$
is always less than 1. Therefore,
${\beta}_{x, \mathrm{peak}}$
is always less than 1. Therefore,
![]() ${a}_{x0}\ge 1$
is required to guarantee the electron phase-locking. As
${a}_{x0}\ge 1$
is required to guarantee the electron phase-locking. As
![]() ${a}_{x0}=2\sqrt{2e}{a}_0/{k}_0{\sigma}_0$
, exact solution for the equations reads
${a}_{x0}=2\sqrt{2e}{a}_0/{k}_0{\sigma}_0$
, exact solution for the equations reads
Figure 2(c)–2(f) present the evolution of the longitudinal electron velocity
![]() ${\beta}_x$
with respect to
${\beta}_x$
with respect to
![]() $\Delta \psi =\psi -{\psi}_0$
for
$\Delta \psi =\psi -{\psi}_0$
for
![]() ${a}_{x0}=0.2$
(dashed) and
${a}_{x0}=0.2$
(dashed) and
![]() $0.998$
(solid), respectively. The maximum nodes
$0.998$
(solid), respectively. The maximum nodes
![]() $\Delta \psi =2 k\pi +\pi /2-{\psi}_0$
remain unchanged for different
$\Delta \psi =2 k\pi +\pi /2-{\psi}_0$
remain unchanged for different
![]() ${a}_{x0}$
. However, the corresponding
${a}_{x0}$
. However, the corresponding
![]() ${\beta}_x$
quickly rises when
${\beta}_x$
quickly rises when
![]() ${a}_{x0}$
increases from
${a}_{x0}$
increases from
![]() $0.2$
to
$0.2$
to
![]() $0.998$
. Considering the Guoy phase and multi-dimensional effects, when Equation (2) is satisfied,
$0.998$
. Considering the Guoy phase and multi-dimensional effects, when Equation (2) is satisfied,
![]() ${\beta}_x$
approaches the speed of light at these nodes so that the electrons remain phased-locked. Therefore, electron bunches may form at
${\beta}_x$
approaches the speed of light at these nodes so that the electrons remain phased-locked. Therefore, electron bunches may form at
![]() $\Delta \psi =2 k\pi +\pi /2-{\psi}_0$
when the CEP is equal to
$\Delta \psi =2 k\pi +\pi /2-{\psi}_0$
when the CEP is equal to
![]() ${\psi}_0$
. However, when
${\psi}_0$
. However, when
![]() ${\psi}_0=3\pi /2$
,
${\psi}_0=3\pi /2$
,
![]() ${\beta}_x$
at the local maximum node
${\beta}_x$
at the local maximum node
![]() $\pi$
and
$\pi$
and
![]() $5\pi$
may be much less than that of the node
$5\pi$
may be much less than that of the node
![]() $3\pi$
, as shown in Figure 2(f). In this case, electrons may be phase-locked only at the node
$3\pi$
, as shown in Figure 2(f). In this case, electrons may be phase-locked only at the node
![]() $3\pi$
. In this way, we may generate an isolated electron bunch by setting the CEP to
$3\pi$
. In this way, we may generate an isolated electron bunch by setting the CEP to
![]() $3\pi /2$
. When the CEP is set to
$3\pi /2$
. When the CEP is set to
![]() $0$
,
$0$
,
![]() $\pi /2$
or
$\pi /2$
or
![]() $\pi$
,
$\pi$
,
![]() ${\beta}_x$
at two local maximum nodes is much larger than that of another node. When the condition in Equation (2) is satisfied, electrons may pile up at the two nodes. Meanwhile, the number of generated
${\beta}_x$
at two local maximum nodes is much larger than that of another node. When the condition in Equation (2) is satisfied, electrons may pile up at the two nodes. Meanwhile, the number of generated
![]() $\gamma$
-ray bunches in the nonlinear Thomson scattering process is determined by the number of electron bunches. The degree of isolation of attosecond electron beams or
$\gamma$
-ray bunches in the nonlinear Thomson scattering process is determined by the number of electron bunches. The degree of isolation of attosecond electron beams or
![]() $\gamma$
-rays is also of importance in the experiments, since non-isolated pulses are not applicable in ultrafast dynamics researches. Thus, the CEP should be set to
$\gamma$
-rays is also of importance in the experiments, since non-isolated pulses are not applicable in ultrafast dynamics researches. Thus, the CEP should be set to
![]() $3\pi /2$
to generate an isolated
$3\pi /2$
to generate an isolated
![]() $\gamma$
-ray bunch, which is consistent with the one-dimensionless model. Furthermore, for a longer pulse duration, the formation of an isolated electron sheet and an isolated
$\gamma$
-ray bunch, which is consistent with the one-dimensionless model. Furthermore, for a longer pulse duration, the formation of an isolated electron sheet and an isolated
![]() $\gamma$
-ray bunch becomes difficult, since electrons will simultaneously bunch at multiple nodes.
$\gamma$
-ray bunch becomes difficult, since electrons will simultaneously bunch at multiple nodes.
To verify the one-dimensionless model, we carry out a series of 3D-PIC simulations by changing the laser CEP
![]() ${\psi}_0$
, and keeping other parameters unchanged. The simulation results are shown in Figure 3. When the CEP
${\psi}_0$
, and keeping other parameters unchanged. The simulation results are shown in Figure 3. When the CEP
![]() ${\psi}_0=0$
, two electron bunches with different density form at
${\psi}_0=0$
, two electron bunches with different density form at
![]() $x=7.75{\lambda}_0$
and
$x=7.75{\lambda}_0$
and
![]() $x=8.75{\lambda}_0$
. When
$x=8.75{\lambda}_0$
. When
![]() ${\psi}_0$
rises to
${\psi}_0$
rises to
![]() $\pi /2$
, the electron bunches are pushed rightwards to
$\pi /2$
, the electron bunches are pushed rightwards to
![]() $8{\lambda}_0$
and
$8{\lambda}_0$
and
![]() $9{\lambda}_0$
, respectively. Meanwhile, the density and energy distributions of the electron bunches also change. When
$9{\lambda}_0$
, respectively. Meanwhile, the density and energy distributions of the electron bunches also change. When
![]() ${\psi}_0$
further increases to
${\psi}_0$
further increases to
![]() $\pi$
, the electron bunches are pushed to the right-hand side further. The electron bunch at
$\pi$
, the electron bunches are pushed to the right-hand side further. The electron bunch at
![]() $x=8.25{\lambda}_0$
is subjected to the peak electric field and its energy achieves maximum. When the CEP
$x=8.25{\lambda}_0$
is subjected to the peak electric field and its energy achieves maximum. When the CEP
![]() ${\psi}_0=3\pi /2$
, there is only one isolated electron bunch at
${\psi}_0=3\pi /2$
, there is only one isolated electron bunch at
![]() $x=8.5{\lambda}_0$
, which is consistent with the one-dimensionless model. In summary, when the CEP
$x=8.5{\lambda}_0$
, which is consistent with the one-dimensionless model. In summary, when the CEP
![]() ${\psi}_0$
increases to
${\psi}_0$
increases to
![]() $\pi /2$
, the electron bunch will be shifted rightwards by about
$\pi /2$
, the electron bunch will be shifted rightwards by about
![]() $0.25{\lambda}_0$
, and the density and energy are also regulated. In particular, when
$0.25{\lambda}_0$
, and the density and energy are also regulated. In particular, when
![]() ${\psi}_0=3\pi /2$
, an isolated dense attosecond electron bunch with higher energy may be generated as electrons are close to the central zone of the laser envelope. We can also increase the number of electron bunches by using a laser pulse with longer pulse duration. It is demonstrated by 3D-PIC simulations that an isolated electron bunch can be produced when the pulse duration
${\psi}_0=3\pi /2$
, an isolated dense attosecond electron bunch with higher energy may be generated as electrons are close to the central zone of the laser envelope. We can also increase the number of electron bunches by using a laser pulse with longer pulse duration. It is demonstrated by 3D-PIC simulations that an isolated electron bunch can be produced when the pulse duration
![]() $2\tau =3{T}_0$
and the CEP
$2\tau =3{T}_0$
and the CEP
![]() ${\psi}_0=3\pi /2$
, which agrees well with our predictions above.
${\psi}_0=3\pi /2$
, which agrees well with our predictions above.

Figure 3 (a)–(d) Electron density distribution at
![]() $t=10{T}_0$
and (e)–(h) corresponding electron energy distribution at
$t=10{T}_0$
and (e)–(h) corresponding electron energy distribution at
![]() $t=30{T}_0$
in the
$t=30{T}_0$
in the
![]() $xoy$
plane when
$xoy$
plane when
![]() ${\psi}_0=0$
,
${\psi}_0=0$
,
![]() $\pi /2$
,
$\pi /2$
,
![]() $\pi$
and
$\pi$
and
![]() $3\pi /2$
, respectively.
$3\pi /2$
, respectively.
2.2. The production of isolated attosecond
 $\gamma$
-rays
$\gamma$
-rays
In our configuration, such an isolated energetic electron bunch collides head-on with a scattering laser pulse. The scattering pulse is a counterstreaming linearly polarized Gaussian laser pulse with a dimensionless peak amplitude of
![]() ${a}_1=45$
. The duration and focal spot radius are
${a}_1=45$
. The duration and focal spot radius are
![]() ${\tau}_1=6{T}_0$
and
${\tau}_1=6{T}_0$
and
![]() ${\sigma}_1=3.5{\lambda}_0$
, respectively. The laser electric field is along the
${\sigma}_1=3.5{\lambda}_0$
, respectively. The laser electric field is along the
![]() $y$
direction. As the duration
$y$
direction. As the duration
![]() ${\tau}_1$
increases, the number, energy and BAM of
${\tau}_1$
increases, the number, energy and BAM of
![]() $\gamma$
-photons also linearly rise (see Figure S8 in the Supplementary Material). Figure 4(a) shows the density distribution of high-energy
$\gamma$
-photons also linearly rise (see Figure S8 in the Supplementary Material). Figure 4(a) shows the density distribution of high-energy
![]() $\gamma$
-photons with energy of more than 1 MeV situated at
$\gamma$
-photons with energy of more than 1 MeV situated at
![]() $x=33.74{\lambda}_0$
,
$x=33.74{\lambda}_0$
,
![]() $33.78{\lambda}_0$
and
$33.78{\lambda}_0$
and
![]() $33.88{\lambda}_0$
. The peak density and corresponding total number of
$33.88{\lambda}_0$
. The peak density and corresponding total number of
![]() $\gamma$
-photons are as high as
$\gamma$
-photons are as high as
![]() $45{n}_{\mathrm{c}}$
and
$45{n}_{\mathrm{c}}$
and
![]() $2.1\times {10}^{10}$
, respectively. The produced
$2.1\times {10}^{10}$
, respectively. The produced
![]() $\gamma$
-photons via nonlinear scattering off electrons show rotations in the same direction as electrons. Figure 4(b) shows the angular distribution of
$\gamma$
-photons via nonlinear scattering off electrons show rotations in the same direction as electrons. Figure 4(b) shows the angular distribution of
![]() $\gamma$
-photons (
$\gamma$
-photons (
![]() ${E}_{\gamma }>1$
MeV), where
${E}_{\gamma }>1$
MeV), where
![]() $\theta$
denotes the angle between the
$\theta$
denotes the angle between the
![]() $x$
-axis and the photon momentum and
$x$
-axis and the photon momentum and
![]() $\phi$
is the crossing angle between the
$\phi$
is the crossing angle between the
![]() $y$
-axis and the transverse momentum of photons. In the polarization plane
$y$
-axis and the transverse momentum of photons. In the polarization plane
![]() $xoy$
, the maximum emission angle of
$xoy$
, the maximum emission angle of
![]() $\gamma$
-photons is
$\gamma$
-photons is
![]() $\sqrt{\theta_{\mathrm{e}}^2+{a}_1^2/{\gamma}_{\mathrm{e}}^2}\approx {4.2}^{\circ }$
, which is consistent with the simulation result of
$\sqrt{\theta_{\mathrm{e}}^2+{a}_1^2/{\gamma}_{\mathrm{e}}^2}\approx {4.2}^{\circ }$
, which is consistent with the simulation result of
![]() ${4}^{\circ }$
. In the orthogonal plane
${4}^{\circ }$
. In the orthogonal plane
![]() $xoz$
, the emission angle approaches
$xoz$
, the emission angle approaches
![]() $\sqrt{\theta_{\mathrm{e}}^2+1/{\gamma}_{\mathrm{e}}^2}\approx {2}^{\circ }$
, in excellent agreement with the simulation results. In classical nonlinear Thomson scattering, it is demonstrated theoretically and experimentally that the
$\sqrt{\theta_{\mathrm{e}}^2+1/{\gamma}_{\mathrm{e}}^2}\approx {2}^{\circ }$
, in excellent agreement with the simulation results. In classical nonlinear Thomson scattering, it is demonstrated theoretically and experimentally that the
![]() $\gamma$
-photons are produced mainly along the polarization direction, and the angular distribution of
$\gamma$
-photons are produced mainly along the polarization direction, and the angular distribution of
![]() $\gamma$
-photons usually peaks at
$\gamma$
-photons usually peaks at
![]() $\phi ={0}^{\circ }$
or
$\phi ={0}^{\circ }$
or
![]() ${180}^{\circ }$
[
Reference Yan, Fruhling, Golovin, Haden, Luo, Zhang, Zhao, Zhang, Liu, Chen, Chen, Banerjee and Umstadter31,
Reference Ji, Pukhov, Kostyukov, Shen and Akli59]. However, the angular distribution in Figure 4(b) is not consistent with this prediction. The distribution of
${180}^{\circ }$
[
Reference Yan, Fruhling, Golovin, Haden, Luo, Zhang, Zhao, Zhang, Liu, Chen, Chen, Banerjee and Umstadter31,
Reference Ji, Pukhov, Kostyukov, Shen and Akli59]. However, the angular distribution in Figure 4(b) is not consistent with this prediction. The distribution of
![]() $\gamma$
-photon divergence is split into two fragments at
$\gamma$
-photon divergence is split into two fragments at
![]() $\phi ={0}^{\circ }$
or
$\phi ={0}^{\circ }$
or
![]() ${180}^{\circ }$
. The average crossing angle between the
${180}^{\circ }$
. The average crossing angle between the
![]() $y$
-axis and each fragment is
$y$
-axis and each fragment is
![]() $\alpha$
. This characteristic is also obvious at
$\alpha$
. This characteristic is also obvious at
![]() $t=45{T}_0$
(see Figures S1(b) and S1(c) in the Supplementary Material). However, if the colliding laser is replaced by a circularly polarized pulse, the angular distribution will become circularly symmetric, as shown in Figure S2(a) (Supplementary Material). Since the rotating attosecond electron sheets carry BAM, we thus deduce that the splitting of divergence distribution may result from the BAM transfer during the photon emission. In the scattering processes
$t=45{T}_0$
(see Figures S1(b) and S1(c) in the Supplementary Material). However, if the colliding laser is replaced by a circularly polarized pulse, the angular distribution will become circularly symmetric, as shown in Figure S2(a) (Supplementary Material). Since the rotating attosecond electron sheets carry BAM, we thus deduce that the splitting of divergence distribution may result from the BAM transfer during the photon emission. In the scattering processes
![]() $\gamma$
-ray photons absorb abundant BAM and gain transverse momentum from the relativistic electron layer, which may result in the splitting of divergence distribution. The unique angular distributions of
$\gamma$
-ray photons absorb abundant BAM and gain transverse momentum from the relativistic electron layer, which may result in the splitting of divergence distribution. The unique angular distributions of
![]() $\gamma$
-ray photons may provide a new signature in the Thomson backscattering experiments to distinguish whether the
$\gamma$
-ray photons may provide a new signature in the Thomson backscattering experiments to distinguish whether the
![]() $\gamma$
-ray beams carry BAM. The BAM transfer during the laser–plasma interaction will be investigated in the following paragraph.
$\gamma$
-ray beams carry BAM. The BAM transfer during the laser–plasma interaction will be investigated in the following paragraph.

Figure 4 (a) Density distribution, (b) angular distribution, (c) energy distribution and (d) energy spectrum and brilliance of high-energy
![]() $\gamma$
-photons with energy of more than 1 MeV at
$\gamma$
-photons with energy of more than 1 MeV at
![]() $t=35{T}_0$
. Here, the magenta arrows in (a) denote the average transverse momentum of
$t=35{T}_0$
. Here, the magenta arrows in (a) denote the average transverse momentum of
![]() $\gamma$
-photons at each cell. The black double-headed arrow in (b) denotes the polarization direction.
$\gamma$
-photons at each cell. The black double-headed arrow in (b) denotes the polarization direction.
After the colliding laser is scattered, the photon energy increases by
![]() $4n{\gamma}_{\mathrm{e}}^2/\left(1+{a}_1^2/2\right)$
based on simultaneous relativistic Doppler upshift and multi-photon absorption, where
$4n{\gamma}_{\mathrm{e}}^2/\left(1+{a}_1^2/2\right)$
based on simultaneous relativistic Doppler upshift and multi-photon absorption, where
![]() $n\propto {a}_1^3$
is the order of harmonics[
Reference Esarey, Ride and Sprangle29,
Reference Yan, Fruhling, Golovin, Haden, Luo, Zhang, Zhao, Zhang, Liu, Chen, Chen, Banerjee and Umstadter31]. Figure 3(c) shows that the energy distribution of
$n\propto {a}_1^3$
is the order of harmonics[
Reference Esarey, Ride and Sprangle29,
Reference Yan, Fruhling, Golovin, Haden, Luo, Zhang, Zhao, Zhang, Liu, Chen, Chen, Banerjee and Umstadter31]. Figure 3(c) shows that the energy distribution of
![]() $\gamma$
-photons is circularly symmetric. Due to
$\gamma$
-photons is circularly symmetric. Due to
![]() ${E}_{\gamma}={p}_{\gamma }c$
, the momentum distribution of
${E}_{\gamma}={p}_{\gamma }c$
, the momentum distribution of
![]() $\gamma$
-photons is also circularly symmetric. Since the maximum
$\gamma$
-photons is also circularly symmetric. Since the maximum
![]() ${\gamma}_{\mathrm{e}}$
is approximately 680 at
${\gamma}_{\mathrm{e}}$
is approximately 680 at
![]() $t=30{T}_0$
, this multi-photon process dominates the nonlinear scattering process so that the
$t=30{T}_0$
, this multi-photon process dominates the nonlinear scattering process so that the
![]() $\gamma$
-photon energy approaches eventually 100 MeV with an average energy of 18.4 MeV, as shown in Figure 4(d). We also calculate the photon brilliance with respect to different photon energy by assuming the root mean square (rms) values of the transverse size of
$\gamma$
-photon energy approaches eventually 100 MeV with an average energy of 18.4 MeV, as shown in Figure 4(d). We also calculate the photon brilliance with respect to different photon energy by assuming the root mean square (rms) values of the transverse size of
![]() $1.7\;\mu \mathrm{m}\times 1.7\;\mu \mathrm{m}$
. It is shown that the peak brilliance of the generated isolated attosecond
$1.7\;\mu \mathrm{m}\times 1.7\;\mu \mathrm{m}$
. It is shown that the peak brilliance of the generated isolated attosecond
![]() $\gamma$
-photons is up to
$\gamma$
-photons is up to
![]() $9.3\times10^{24}$
photons s
$9.3\times10^{24}$
photons s
![]() ${}^{-1}$
mrad
${}^{-1}$
mrad
![]() ${}^{-2}$
mm
${}^{-2}$
mm
![]() ${}^{-2}$
per 0.1
${}^{-2}$
per 0.1
![]() $\%$
bandwidth at 4.3 MeV.
$\%$
bandwidth at 4.3 MeV.
3. Discussion
In order to investigate the OAM transfer during the laser–plasma interaction, we present the evolution of total energy and BAM of electrons and
![]() $\gamma$
-photons in Figure 5(a). Since the electron layer is generated and phase-locked, electrons are continuously accelerated by the twisted laser pulse. The total electron energy (
$\gamma$
-photons in Figure 5(a). Since the electron layer is generated and phase-locked, electrons are continuously accelerated by the twisted laser pulse. The total electron energy (
![]() ${E}_{t,\mathrm{e}}$
) and BAM (
${E}_{t,\mathrm{e}}$
) and BAM (
![]() ${L}_{t,\mathrm{e}}$
) synchronously increase, where
${L}_{t,\mathrm{e}}$
) synchronously increase, where
![]() ${L}_{t,\mathrm{e}}={\sum}_{i=1}^n\left({y}_i{p}_{z,i}-{z}_i{p}_{y,i}\right)$
with
${L}_{t,\mathrm{e}}={\sum}_{i=1}^n\left({y}_i{p}_{z,i}-{z}_i{p}_{y,i}\right)$
with
![]() ${y}_i,\,{z}_i,\,{p}_{z,i}$
and
${y}_i,\,{z}_i,\,{p}_{z,i}$
and
![]() ${p}_{y,i}$
being the electron transverse coordinates and momentum, respectively. It is shown that the
${p}_{y,i}$
being the electron transverse coordinates and momentum, respectively. It is shown that the
![]() ${E}_{t,\mathrm{e}}$
and
${E}_{t,\mathrm{e}}$
and
![]() ${L}_{t,\mathrm{e}}$
achieved are 0.38 J and
${L}_{t,\mathrm{e}}$
achieved are 0.38 J and
![]() $3.1\times {10}^{17}\mathrm{\hslash}$
at
$3.1\times {10}^{17}\mathrm{\hslash}$
at
![]() $t=31{T}_0$
, respectively. When the flying electron layer encounters the counter-propagating laser pulse at
$t=31{T}_0$
, respectively. When the flying electron layer encounters the counter-propagating laser pulse at
![]() $t=31{T}_0$
, the electron energy and total BAM are simultaneously transferred to the
$t=31{T}_0$
, the electron energy and total BAM are simultaneously transferred to the
![]() $\gamma$
-photons via nonlinear Thomson scattering so that both the electron total energy and BAM decrease. Our simulations indicate that about
$\gamma$
-photons via nonlinear Thomson scattering so that both the electron total energy and BAM decrease. Our simulations indicate that about
![]() $9.8\%$
electron energy and
$9.8\%$
electron energy and
![]() $9.4\%$
BAM are transferred to
$9.4\%$
BAM are transferred to
![]() $\gamma$
-photons in this nonlinear process. This is the reason why the
$\gamma$
-photons in this nonlinear process. This is the reason why the
![]() $\gamma$
-photon energy and BAM sharply rise from
$\gamma$
-photon energy and BAM sharply rise from
![]() $t=31{T}_0$
. Finally, the total photon energy and BAM reach 0.037 J and
$t=31{T}_0$
. Finally, the total photon energy and BAM reach 0.037 J and
![]() $2.8\times {10}^{16}\mathrm{\hslash}$
, respectively, after which both saturate due to the termination of laser interaction. Due to the high transfer efficiency of BAM, the BAM of
$2.8\times {10}^{16}\mathrm{\hslash}$
, respectively, after which both saturate due to the termination of laser interaction. Due to the high transfer efficiency of BAM, the BAM of
![]() $\gamma$
-photons here is four orders of magnitude higher than that using nonlinear Compton scattering of an intense twisted laser pulse at ultra-relativistic electrons with
$\gamma$
-photons here is four orders of magnitude higher than that using nonlinear Compton scattering of an intense twisted laser pulse at ultra-relativistic electrons with
![]() ${\gamma}_{\mathrm{e}}={10}^4$
[
Reference Chen, Li, Hatsagortsyan and Keitel23].
${\gamma}_{\mathrm{e}}={10}^4$
[
Reference Chen, Li, Hatsagortsyan and Keitel23].

Figure 5 (a) Evolution of energy and BAM for electrons and
![]() $\gamma$
-photons. (b) Distribution of the average OAM
$\gamma$
-photons. (b) Distribution of the average OAM
![]() $\overline{L}$
along energy
$\overline{L}$
along energy
![]() $E$
. (c) Spectrum of
$E$
. (c) Spectrum of
![]() $L$
for electrons and
$L$
for electrons and
![]() $\gamma$
-photons. Influence of the laser intensity
$\gamma$
-photons. Influence of the laser intensity
![]() ${a}_0$
on the (d) energy and BAM conversion efficiency
${a}_0$
on the (d) energy and BAM conversion efficiency
![]() ${\eta}_{\mathrm{E}}$
and
${\eta}_{\mathrm{E}}$
and
![]() ${\eta}_{\mathrm{L}}$
, (e) energy spectrum and (f) brilliance of
${\eta}_{\mathrm{L}}$
, (e) energy spectrum and (f) brilliance of
![]() $\gamma$
-photons.
$\gamma$
-photons.
We provide in the following a simple model to explain the BAM transfer process. Here the average photon energy
![]() ${\overline{E}}_{\gamma}={\overline{p}}_{\gamma }c$
while the average electron energy
${\overline{E}}_{\gamma}={\overline{p}}_{\gamma }c$
while the average electron energy
![]() ${\overline{E}}_{\mathrm{e}}=\left({\overline{\gamma}}_{\mathrm{e}}-1\right){m}_{\mathrm{e}0}{c}^2\approx {\overline{p}}_{\mathrm{e}}c$
when
${\overline{E}}_{\mathrm{e}}=\left({\overline{\gamma}}_{\mathrm{e}}-1\right){m}_{\mathrm{e}0}{c}^2\approx {\overline{p}}_{\mathrm{e}}c$
when
![]() ${\gamma}_{\mathrm{e}}\gg 1$
. Therefore, the average energy of
${\gamma}_{\mathrm{e}}\gg 1$
. Therefore, the average energy of
![]() $\gamma$
-photons and electrons satisfies
$\gamma$
-photons and electrons satisfies
![]() ${\overline{E}}_{\gamma }/{\overline{E}}_{\mathrm{e}}\approx {\overline{p}}_{\gamma }/{\overline{p}}_{\mathrm{e}}$
. As
${\overline{E}}_{\gamma }/{\overline{E}}_{\mathrm{e}}\approx {\overline{p}}_{\gamma }/{\overline{p}}_{\mathrm{e}}$
. As
![]() $\gamma$
-photons inherit the position of the parent electrons during the scattering process, the average OAM of
$\gamma$
-photons inherit the position of the parent electrons during the scattering process, the average OAM of
![]() $\gamma$
-photons and electrons satisfies
$\gamma$
-photons and electrons satisfies
![]() ${\overline{L}}_{\gamma }/{\overline{L}}_{\mathrm{e}}={\overline{p}}_{\gamma }/{\overline{p}}_{\mathrm{e}}$
[
Reference Wang, Li, Gan, Xie, Zhong, Zhou, Zhu, He and Qiao20]. Therefore, the ratio of average energy and OAM for
${\overline{L}}_{\gamma }/{\overline{L}}_{\mathrm{e}}={\overline{p}}_{\gamma }/{\overline{p}}_{\mathrm{e}}$
[
Reference Wang, Li, Gan, Xie, Zhong, Zhou, Zhu, He and Qiao20]. Therefore, the ratio of average energy and OAM for
![]() $\gamma$
-photons and electrons
$\gamma$
-photons and electrons
![]() ${\overline{E}}_{\gamma }/{\overline{E}}_{\mathrm{e}}\approx {\overline{L}}_{\gamma }/{\overline{L}}_{\mathrm{e}}$
. The ratio of total energy and BAM for
${\overline{E}}_{\gamma }/{\overline{E}}_{\mathrm{e}}\approx {\overline{L}}_{\gamma }/{\overline{L}}_{\mathrm{e}}$
. The ratio of total energy and BAM for
![]() $\gamma$
-photons and electrons approaches the following:
$\gamma$
-photons and electrons approaches the following:
which indicates that the electron energy and BAM are transferred to the
![]() $\gamma$
-photons for the same proportion as given in Figure 5(a). Therefore, we can obtain the BAM of
$\gamma$
-photons for the same proportion as given in Figure 5(a). Therefore, we can obtain the BAM of
![]() $\gamma$
-rays from the energy conversion efficiency from electrons to
$\gamma$
-rays from the energy conversion efficiency from electrons to
![]() $\gamma$
-photons
$\gamma$
-photons
![]() ${\eta}_{\mathrm{E}}$
. It is interesting to see that for electrons or photons with different energy, as shown in Figure 5(b), the ratio of the average OAM
${\eta}_{\mathrm{E}}$
. It is interesting to see that for electrons or photons with different energy, as shown in Figure 5(b), the ratio of the average OAM
![]() $\overline{L}$
and the average energy
$\overline{L}$
and the average energy
![]() $\overline{E}$
is approximately equal, namely
$\overline{E}$
is approximately equal, namely
![]() ${\overline{L}}_{\mathrm{e}}/{\overline{E}}_{\mathrm{e}}\approx {\overline{L}}_{\gamma }/{\overline{E}}_{\gamma }$
, which is consistent with the above deduction. Figure 5(c) presents the spectrum of
${\overline{L}}_{\mathrm{e}}/{\overline{E}}_{\mathrm{e}}\approx {\overline{L}}_{\gamma }/{\overline{E}}_{\gamma }$
, which is consistent with the above deduction. Figure 5(c) presents the spectrum of
![]() $L$
for electrons and
$L$
for electrons and
![]() $\gamma$
-photons. The electron OAM ranges from 0 to 1.0
$\gamma$
-photons. The electron OAM ranges from 0 to 1.0
![]() $\times$
10
$\times$
10
![]() ${}^8\mathrm{\hslash}$
and is along the positive
${}^8\mathrm{\hslash}$
and is along the positive
![]() $x$
-axis. However, the
$x$
-axis. However, the
![]() $L$
spectrum of
$L$
spectrum of
![]() $\gamma$
-photons is much narrower. Due to the linear relation of the OAM
$\gamma$
-photons is much narrower. Due to the linear relation of the OAM
![]() $L$
and energy
$L$
and energy
![]() $E$
,
$E$
,
![]() $\gamma$
-photons with low energy carry low
$\gamma$
-photons with low energy carry low
![]() $L$
. Since low-energy photons are in the majority, the
$L$
. Since low-energy photons are in the majority, the
![]() $L$
spectrum of
$L$
spectrum of
![]() $\gamma$
-photons has a peak near
$\gamma$
-photons has a peak near
![]() $L=0$
.
$L=0$
.
We also investigate the evolution of the
![]() $\gamma$
-photon energy and BAM in the case of a circularly polarized Gaussian scattering pulse with the same pulse energy. It is shown that the evolutions of
$\gamma$
-photon energy and BAM in the case of a circularly polarized Gaussian scattering pulse with the same pulse energy. It is shown that the evolutions of
![]() $\gamma$
-photon energy and BAM are similar in both cases. Because the energy and BAM of the
$\gamma$
-photon energy and BAM are similar in both cases. Because the energy and BAM of the
![]() $\gamma$
-photons originate mainly from the electron layer according to Equation (3), the polarization of the scattering laser pulse does not influence the final photon energy and BAM (see Figure S2 in the Supplementary Material). As the laser intensity
$\gamma$
-photons originate mainly from the electron layer according to Equation (3), the polarization of the scattering laser pulse does not influence the final photon energy and BAM (see Figure S2 in the Supplementary Material). As the laser intensity
![]() ${a}_0$
increases, the total energy and BAM of electrons or
${a}_0$
increases, the total energy and BAM of electrons or
![]() $\gamma$
-photons quickly rise (see Figure S3 in the Supplementary Material). Meanwhile, the energy and BAM conversion efficiency
$\gamma$
-photons quickly rise (see Figure S3 in the Supplementary Material). Meanwhile, the energy and BAM conversion efficiency
![]() ${\eta}_{\mathrm{E}}$
and
${\eta}_{\mathrm{E}}$
and
![]() ${\eta}_{\mathrm{L}}$
also rise linearly. Furthermore, the electron energy and BAM are transferred to the
${\eta}_{\mathrm{L}}$
also rise linearly. Furthermore, the electron energy and BAM are transferred to the
![]() $\gamma$
-photons for the same proportion, that is,
$\gamma$
-photons for the same proportion, that is,
![]() ${\eta}_{\mathrm{E}}\approx {\eta}_{\mathrm{L}}$
. Figures 5(e) and 5(f) show the energy spectrum and brilliance of
${\eta}_{\mathrm{E}}\approx {\eta}_{\mathrm{L}}$
. Figures 5(e) and 5(f) show the energy spectrum and brilliance of
![]() $\gamma$
-photons. As the laser intensity increases, the average energy and duration of the
$\gamma$
-photons. As the laser intensity increases, the average energy and duration of the
![]() $\gamma$
-photons also rise. When the laser intensity
$\gamma$
-photons also rise. When the laser intensity
![]() ${a}_0=30$
, the peak brilliance of the generated isolated attosecond
${a}_0=30$
, the peak brilliance of the generated isolated attosecond
![]() $\gamma$
-photons is maximal, which is up to 1.0
$\gamma$
-photons is maximal, which is up to 1.0
![]() $\times$
10
$\times$
10
![]() ${}^{25}$
photons s
${}^{25}$
photons s
![]() ${}^{-1}$
mrad
${}^{-1}$
mrad
![]() ${}^{-2}$
mm
${}^{-2}$
mm
![]() ${}^{-2}$
per 0.1
${}^{-2}$
per 0.1
![]() $\%$
bandwidth at 2.1 MeV. Therefore, we can manipulate the energy, BAM and brilliance of
$\%$
bandwidth at 2.1 MeV. Therefore, we can manipulate the energy, BAM and brilliance of
![]() $\gamma$
-rays by changing the drive laser intensity
$\gamma$
-rays by changing the drive laser intensity
![]() ${a}_0$
. We also investigate the influence of the initial plasma density and the droplet radius. It is shown that the main simulation results remain unchanged when the initial electron density increases to
${a}_0$
. We also investigate the influence of the initial plasma density and the droplet radius. It is shown that the main simulation results remain unchanged when the initial electron density increases to
![]() $50{n}_{\mathrm{c}}$
or the droplet radius increases from
$50{n}_{\mathrm{c}}$
or the droplet radius increases from
![]() $0.5{\lambda}_0$
to
$0.5{\lambda}_0$
to
![]() $1.5{\lambda}_0$
(see Figures S4–S6 in the Supplementary Material). The robustness of the scheme has been also confirmed by the simulations with consideration of the pre-expansion of the micro-droplet target (see Figure S7 in the Supplementary Material).
$1.5{\lambda}_0$
(see Figures S4–S6 in the Supplementary Material). The robustness of the scheme has been also confirmed by the simulations with consideration of the pre-expansion of the micro-droplet target (see Figure S7 in the Supplementary Material).
4. Conclusions
In conclusion, we have proposed a new all-optical scheme to generate ultra-brilliant attosecond
![]() $\gamma$
-ray beams with BAM via the nonlinear Thomson scattering of a counter-propagating intense laser pulse off a laser-driven ultra-relativistic electron sheet from a micro-droplet target. This work should promote the experimental investigation of nonlinear Thomson scattering of rotating electron sheets in large laser facilities. The achieved singe isolated
$\gamma$
-ray beams with BAM via the nonlinear Thomson scattering of a counter-propagating intense laser pulse off a laser-driven ultra-relativistic electron sheet from a micro-droplet target. This work should promote the experimental investigation of nonlinear Thomson scattering of rotating electron sheets in large laser facilities. The achieved singe isolated
![]() $\gamma$
-ray beam with ultra-high brilliance, small divergence and large BAM has potential applications in nuclear physics, astrophysics, radiography of dense objects and diagnosis for laser–plasma interaction.
$\gamma$
-ray beam with ultra-high brilliance, small divergence and large BAM has potential applications in nuclear physics, astrophysics, radiography of dense objects and diagnosis for laser–plasma interaction.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Nos. 12105362, 12375244, 12275356, 12135009, U2241281 and 12175310), the Natural Science Foundation of Hunan Province (No. 2022JJ20042) and the Innovation Foundation for Graduate Students (No. CX20220048).
Supplementary material
The supplementary material for this article can be found at https://doi.org/10.1017/hpl.2024.66.