Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-01-09T21:12:30.449Z Has data issue: false hasContentIssue false
  • English
  • Français

On Functional Properties of Incomplete Gaussian Sums

Published online by Cambridge University Press:  20 November 2018

K. I. Oskolkov
K. I. Oskolkov*
Affiliation:
Steklov Mathematical Institute of the Academy of Sciences of the USSR Vavilov str, 42, Moscow GSP-1 USSR 117966
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

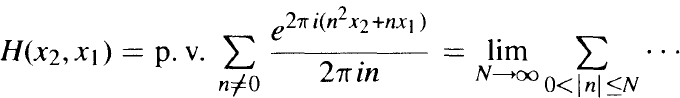The following special function of two real variables x2 and x1 is considered: and its connections with the incomplete Gaussian sums 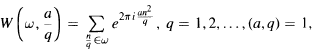where ω are intervals of length |ω| ≤1. In particular, it is proved that for each fixed x2 and uniformly in X2 the function H(x2, x1) is of weakly bounded 2-variation in the variable x1 over the period [0, 1]. In terms of the sums W this means that for collections Ω = {ωk}, consisting of nonoverlapping intervals ωk ∪ [0,1) the following estimate is valid: 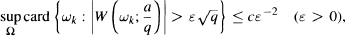where card denotes the number of elements, and c is an absolute positive constant. The exact value of the best absolute constant к in the estimate 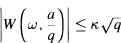(which is due to G. H. Hardy and J. E. Littlewood) is discussed.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 43 , Issue 1 , 01 February 1991 , pp. 182 - 212
Copyright
Copyright © Canadian Mathematical Society 1991

References

1. Arkhipov, G.I., Oskolkov, K.I., Ob odnom special'nom trigonometricheskom ryade i ego primeneniyah, Matematicheskii Sbornik, 134(176), (1987), No. 2(10), 147-157; in English: On a special trigonometric series and its applications, Math. USSR Sbornik, 62(1989), No. 1, 145–155.Google Scholar
2. Bary, N.K., A treatise on trigonometric series. 1, Pergamon Press, N.Y., 1964.Google Scholar
3. Bary, N.K., Beijing Lectures in harmonic analysis. ed. by Stein, E.M., Princeton Univ. Press, Princeton, New Jersey, 1986.Google Scholar
3i ibid. Stein, E.M., Oscillatory integrals in Fourier analysis, 307–355.Google Scholar
3ii ibid Stephen Wainger, Averages and singular integrals over lower dimensional sets, 357–421.Google Scholar
4. Fiedler, H., Jurkat, W., Koerner, O., Asymptotic expansions of finite theta series, Acta Arithmetica, 32(1977), 129–146.Google Scholar
5. Hardy, G.H. and Littlewood, J.E., Some problems of Diophantine approximation, II. The trigonometrical series associated with the elliptic 9 -functions, Acta Mathematica 37(1914), 193–238.Google Scholar
5i Hardy, G.H. and Littlewood, J.E., Collected papers of G.H. Hardy, Oxford: Clarendon Press(1966),l.Google Scholar
6. Oskolkov, K.I., O svoistvah odnogo klassa ryadov IM. Vinogradova, Doklady AN SSSR, 300, No. 4(1988), 803–807.Google Scholar
6i Oskolkov, K.I., Ryady i integraly IM. Vinogradova i ih prilo ženiya, Trudy MIAN SSSR, 190(1989), 186–221.Google Scholar
7. Stein, E.M. and Wainger, S., The estimation of an integral arising in multiplier transformations, Studia Math., 35(1970), 101–104.Google Scholar
8. Vinogradov, I.M., Metod trigonometricheskih summ v teorii chisel, Moscow: Nauka (1980).Google Scholar
9. Vinogradov, I.M., Osnovy teorii chisel, 8th ed., Nauka, Moskva (1972); in English: Elements of number theory, transi, fith revised éd., Dover Pub., Inc. (1954).Google Scholar
10. Zygmund, A., Trigonometric series 1, Cambridge Univ. Press, (1959).Google Scholar