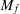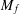Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Nowicka, Monika
and
Witkowski, Alfred
2015.
A refinement of the left-hand side of Hermite-Hadamard inequality for simplices.
Journal of Inequalities and Applications,
Vol. 2015,
Issue. 1,
Li, Zhengbo
Kamran
Zahoor, Muhammad Sajid
Akhtar, Huma
and
Kumar, Sunil
2020.
Hermite–Hadamard and Fractional Integral Inequalities for Interval-Valued Generalized
p
-Convex Function.
Journal of Mathematics,
Vol. 2020,
Issue. ,
p.
1.
Jung, Chahn Yong
Saleem, Muhammad Shoaib
Bilal, Shamas
Nazeer, Waqas
and
Ghafoor, Mamoona
2021.
Some properties of <i>η</i>-convex stochastic processes.
AIMS Mathematics,
Vol. 6,
Issue. 1,
p.
726.
Raïssouli, Mustapha
2022.
Refining the Hermite-Hadamard inequalities for operator convex maps in multiple operator variables.
Aequationes mathematicae,
Vol. 96,
Issue. 4,
p.
803.
Raïssouli, Mustapha
2023.
Further refinements and reverses of the Hermite–Hadamard inequalities for multivariate operator convex maps.
Advances in Operator Theory,
Vol. 8,
Issue. 1,
Samraiz, Muhammad
Atta, Tahira
Naheed, Saima
Abdeljawad, Thabet
and
Ghaffar, Muhammad Tanveer
2024.
A novel class of integral inequalities with graphical approach and diverse applications.
Mathematical and Computer Modelling of Dynamical Systems,
Vol. 30,
Issue. 1,
p.
156.