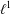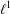Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kelarev, Andrei V.
Susilo, Willy
Miller, Mirka
and
Ryan, Joe
2016.
Ideals of Largest Weight in Constructions Based on Directed Graphs.
Bulletin of Mathematical Sciences and Applications,
Vol. 15,
Issue. ,
p.
8.
Esslamzadeh, G. H.
2017.
Homomorphisms of $$\ell ^1$$ ℓ 1 -Munn algebras and Rees matrix semigroup algebras.
Semigroup Forum,
Vol. 95,
Issue. 1,
p.
1.
Minapoor, Ahmad
2021.
Ideal Connes amenability of $$l^{1}$$-Munn algebras and its application to semigroup algebras.
Semigroup Forum,
Vol. 102,
Issue. 3,
p.
756.
Rostami, M.
Shariati, S. F.
Sahami, A.
and
Rafeiro, Humberto
2022.
On Amenability‐Like Properties of a Class of Matrix Algebras.
Journal of Mathematics,
Vol. 2022,
Issue. 1,