Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2025-01-02T18:14:57.891Z Has data issue: false hasContentIssue false
  • English
  • Français

DIRECTIONAL MAXIMAL OPERATORS AND RADIAL WEIGHTS ON THE PLANE

Part of: Harmonic analysis in several variables

Published online by Cambridge University Press:  12 September 2013

HIROKI SAITO  and
HITOSHI TANAKA
HIROKI SAITO*
Affiliation:
Tokyo Metropolitan University, 1-1 Minami-Ohsawa, Hachioji-shi, Tokyo 192-0397, Japan
HITOSHI TANAKA
Affiliation:
Graduate School of Mathematical Sciences, University of Tokyo, Tokyo 153-8914, Japan email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 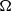$\Omega $ be the set of unit vectors and 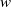$w$ be a radial weight on the plane. We consider the weighted directional maximal operator defined by

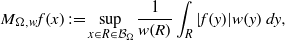$$\begin{eqnarray*}{M}_{\Omega , w} f(x): = \sup _{x\in R\in \mathcal{B} _{\Omega }}\frac{1}{w(R)} \int \nolimits \nolimits_{R} \vert f(y)\vert w(y)\hspace{0.167em} dy,\end{eqnarray*}$$
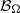where ${ \mathcal{B} }_{\Omega } $ denotes the set of all rectangles on the plane whose longest side is parallel to some unit vector in 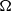$\Omega $ and $w(R)$ denotes 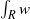$\int \nolimits \nolimits_{R} w$. In this paper we prove an almost-orthogonality principle for this maximal operator under certain conditions on the weight. The condition allows us to get the weighted norm inequality
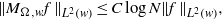$$\begin{eqnarray*}\Vert {M}_{\Omega , w} f\mathop{\Vert }\nolimits_{{L}^{2} (w)} \leq C\log N\Vert f\mathop{\Vert }\nolimits_{{L}^{2} (w)} ,\end{eqnarray*}$$
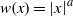 when $w(x)= \vert x\hspace{-1.2pt}\mathop{\vert }\nolimits ^{a} $, 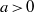$a\gt 0$, and when 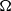$\Omega $ is the set of unit vectors on the plane with cardinality 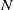$N$ sufficiently large.

Keywords

almost-orthogonality principledirectional maximal operatorradial weightstrong-type estimate

MSC classification

Secondary: 42B25: Maximal functions, Littlewood-Paley theory
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 89 , Issue 3 , June 2014 , pp. 397 - 414
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Alfonseca, A., Soria, F. and Vargas, A., ‘A remark on maximal operators along directions in ${ \mathbb{R} }^{2} $’, Math. Res. Lett. 10 (1) (2003), 41–49.CrossRefGoogle Scholar
Alfonseca, A., Soria, F. and Vargas, A., ‘An almost-orthogonality principle in ${L}^{2} $ for directional maximal functions’, in: Harmonic Analysis at Mount Holyoke (South Hadley, MA, 2001), Contemporary Mathematics, 320 (American Mathematical Society, Providence, RI, 2003), 1–7.Google Scholar
Carbery, A., ‘Covering lemmas revisited’, Proc. Edinburgh Math. Soc. (2) 31 (1) (1988), 145–150.Google Scholar
Carbery, A., Hernández, E. and Soria, F., ‘Estimates for the Kakeya maximal operator on radial functions in ${ \mathbb{R} }^{n} $’, in: Harmonic Analysis, ICM-90 Satellite Conference Proceedings (ed. Igari, S.) (Springer, Tokyo, 1991), 41–50.Google Scholar
Córdoba, A., ‘The Kakeya maximal function and the spherical summation multiplier’, Amer. J. Math. 99 (1) (1977), 1–22.Google Scholar
Duoandikoetxea, J. and Naibo, V., ‘The universal maximal operator on special classes of functions’, Indiana Univ. Math. J. 54 (5) (2005), 1351–1369.CrossRefGoogle Scholar
García-Cuerva, J. and Rubio de Francia, J. L., Weighted Norm Inequalities and Related Topics (North-Holland, Amsterdam, 1985).Google Scholar
Igari, S., ‘On Kakeya’s maximal function’, Proc. Japan Acad. Ser. A 62 (8) (1986), 292–293.CrossRefGoogle Scholar
Katz, N. H., ‘Maximal operators over arbitrary sets of directions’, Duke Math. J. 97 (1) (1999), 67–79.CrossRefGoogle Scholar
Katz, N. H., ‘Remarks on maximal operators over arbitrary sets of directions’, Bull. Lond. Math. Soc. 31 (6) (1999), 700–710.CrossRefGoogle Scholar
Kurtz, D. S., ‘Littlewood–Paley and multiplier theorems on weighted ${L}^{p} $ spaces’, Trans. Amer. Math. Soc. 259 (1) (1980), 235–254.Google Scholar
Strömberg, J.-O., ‘Maximal functions associated to rectangles with uniformly distributed directions’, Ann. of Math. (2) 107 (2) (1978), 399–402.CrossRefGoogle Scholar
Tanaka, H., ‘An elementary proof of an estimate for the Kakeya maximal operator on functions of product type’, Tohoku Math. J. (2) 48 (3) (1996), 429–435.CrossRefGoogle Scholar
Tanaka, H., ‘An estimate for the Kakeya maximal operator on functions of square radial type’, Tokyo J. Math. 22 (2) (1999), 391–398.Google Scholar