In this paper we present a general, theoretical foundation for the construction of cubature formulae to approximate multivariate integrals. The focus is on cubature formulae that are exact for certain vector spaces of polynomials. Our main quality criteria are the algebraic and trigonometric degrees. The constructions using ideal theory and invariant theory are outlined. The known lower bounds for the number of points are surveyed and characterizations of minimal cubature formulae are given. We include references to all known minimal cubature formulae. Finally, some methods to construct cubature formulae illustrate the previously introduced concepts and theorems.

More than anything else, the increase of computing power seems to stimulate the greed for tackling ever larger problems involving large-scale numerical simulation. As a consequence, the need for understanding something like the intrinsic complexity of a problem occupies a more and more pivotal position. Moreover, computability often only becomes feasible if an algorithm can be found that is asymptotically optimal. This means that storage and the number of floating point operations needed to resolve the problem with desired accuracy remain proportional to the problem size when the resolution of the discretization is refined. A significant reduction of complexity is indeed often possible, when the underlying problem admits a continuous model in terms of differential or integral equations. The physical phenomena behind such a model usually exhibit characteristic features over a wide range of scales. Accordingly, the most successful numerical schemes exploit in one way or another the interaction of different scales of discretization. A very prominent representative is the multigrid methodology; see, for instance, Hackbusch (1985) and Bramble (1993). In a way it has caused a breakthrough in numerical analysis since, in an important range of cases, it does indeed provide asymptotically optimal schemes. For closely related multilevel techniques and a unified treatment of several variants, such as multiplicative or additive subspace correction methods, see Bramble, Pasciak and Xu (1990), Oswald (1994), Xu (1992), and Yserentant (1993). Although there remain many unresolved problems, multigrid or multilevel schemes in the classical framework of finite difference and finite element discretizations exhibit by now a comparatively clear profile. They are particularly powerful for elliptic and parabolic problems.

We introduce a new version of the Fast Multipole Method for the evaluation of potential fields in three dimensions. It is based on a new diagonal form for translation operators and yields high accuracy at a reasonable cost.

Among the iterative methods for solving large linear systems with a sparse (or, possibly, structured) nonsymmetric matrix, those that are based on the Lanczos process feature short recurrences for the generation of the Krylov space. This means low cost and low memory requirement. This review article introduces the reader not only to the basic forms of the Lanczos process and some of the related theory, but also describes in detail a number of solvers that are based on it, including those that are considered to be the most efficient ones. Possible breakdowns of the algorithms and ways to cure them by look-ahead are also discussed.

Let P(x) = 0 be a system of n polynomial equations in n unknowns. Denoting P = (p1,…, pn), we want to find all isolated solutions of

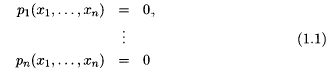
for x = (x1,…,xn). This problem is very common in many fields of science and engineering, such as formula construction, geometric intersection problems, inverse kinematics, power flow problems with PQ-specified bases, computation of equilibrium states, etc. Elimination theory-based methods, most notably the Buchberger algorithm (Buchberger 1985) for constructing Gröbner bases, are the classical approach to solving (1.1), but their reliance on symbolic manipulation makes those methods seem somewhat unsuitable for all but small problems.

One of the most difficult problems in the numerical solution of ordinary differential equations (ODEs) and in differential-algebraic equations (DAEs) is the development of methods for dealing with highly oscillatory systems. These types of systems arise, for example, in vehicle simulation when modelling the suspension system or tyres, in models for contact and impact, in flexible body simulation from vibrations in the structural model, in molecular dynamics, in orbital mechanics, and in circuit simulation. Standard numerical methods can require a huge number of time-steps to track the oscillations, and even with small stepsizes they can alter the dynamics, unless the method is chosen very carefully.

The progressive miniaturization of semiconductor devices, and the use of bulk materials other than silicon, necessitates the use of a wide variety of models in semiconductor device simulation. These include classical and semiclassical models, such as the Boltzmann equation and the hydrodynamic system, as well as quantum transport models such as the quantum Boltzmann equation and the quantum hydrodynamic system. This paper gives an overview of recently developed numerical methods for these systems. The focus is on Galerkin methods for the semiclassical and quantum kinetic systems and on difference methods for the classical and quantum hydrodynamic systems. The stability and convergence properties of these methods and their relation to the analytical properties of the continuous systems are discussed.

Complexity theory of numerical analysis is the study of the number of arithmetic operations required to pass from the input to the output of a numerical problem.