In this section we discuss a very simple problem. Consider the scalar initial value problem
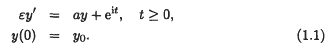
Here ε > 0 is a small constant and a = a1 + ia2, a1, a2 real, is a complex number with |a| = 1. We can write down the solution of (1.1) explicity. It is
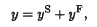
where
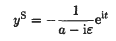
is the forced solution and
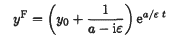
is a solution of the homogeneous equation
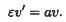
yS varies on the time scale ‘1’ while yF varies on the much faster scale 1/ε. We say that yS, yF vary on the slow and fast scale, respectively. We use also the phrase: yS and yF are the slow and the fast part of the solution, respectively.