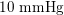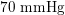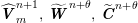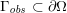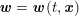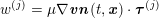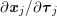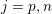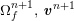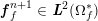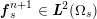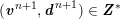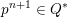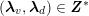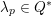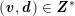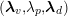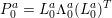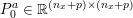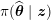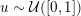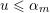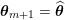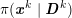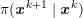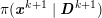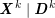1 Introduction
This is a review paper on the mathematical and numerical modelling of the cardiovascular system, a research topic that has attracted remarkable interest from both the mathematical and bioengineering communities over the past 25 years. The driving motivation for this interest is the increasing impact of cardiovascular diseases in our lives. According to Mozaffarian et al. (Reference Mozaffarian, Benjamin, Go, Arnett, Blaha, Cushman, Das, de Ferranti, Després, Fullerton, Howard, Huffman, Isasi, Jiménez, Judd, Kissela, Lichtman, Lisabeth, Liu, Mackey, Magid, McGuire, Mohler, Moy, Muntner, Mussolino, Nasir, Neumar, Nichol, Palaniappan, Pandey, Reeves, Rodriguez, Rosamond, Sorlie, Stein, Towfighi, Turan, Virani, Woo, Yeh and Turner2015), cardiovascular diseases are the major cause of death worldwide, leading to more than 17.3 million deaths per year, a number that is expected to grow to more than 23.6 million by 2030. In Europe this now corresponds to nearly half of all deaths (47%).
In this paper we focus on the two principal components of the cardiovascular system: arterial circulation and heart function, with its electrical and mechanical activities. Geometric complexity, lack of data to feed the mathematical models, and the multiphysics and multiscale nature of the processes at hand present major challenges when trying to reproduce both function and malfunction.
Owing to its composite nature, the cardiovascular system is first modelled by means of stand-alone core components, each describing a single functionality, for example arterial fluid dynamics, the electrical activity of the heart, and the fluid dynamics in the left ventricle. Each core model needs careful mathematical analysis and efficient numerical approximation, often via specifically devised methods. The next step is integration of the core models into global, coupled integrated models suitable for describing a meaningful and coherent part of the cardiovascular system – or even the entire system. This step requires the introduction of suitable coupling conditions and novel numerical strategies for a stable, robust and computationally effective solution of the global problem.
Clinical data play a decisive role in models of the cardiovascular system, and at the same time they present a formidable challenge. Clinical radiological images (such as computer tomography and magnetic resonance imaging) are necessary to construct the computational domains. The procedure of geometric reconstruction is difficult and, especially for the heart, requires advanced mathematical and numerical tools. Standard radiological images can sometimes be useless: some cardiovascular components may be smaller than the spatial resolution of the imaging device (this is the case for the Purkinje network, for example); in other cases the elevated brightness gap between fluid and vessel wall makes the detection of the latter very hard. Boundary data are also difficult to obtain. When the computational domain results from an artificial truncation, specific physical quantities (e.g. fluid velocity or pressure) should be provided at those locations of the arterial tree corresponding to the artificial boundaries. However, this would require invasive measurements that cannot be easily carried out. Finally, the huge inter- and intra-patient data variability and uncertainty are further sources of concern regarding model calibration and validation.
In spite of all these difficulties, a wealth of models has already been successfully used to address both physiological and pathological instances. The aim is, on one hand, a better understanding of the physical and quantitative processes governing the cardiovascular system, and on the other hand the opening of new frontiers in therapeutic planning and the design of implantable devices (e.g. medical stents and cardiac defibrillators).
The literature on the mathematical and numerical modelling of the cardiovascular system is huge, as readers will see by browsing our references, a tiny subset of the total. In the forthcoming sections we will try to provide a perspective on the main contributions to this field. Here, among the several books, monographs and review papers published so far, we mention Formaggia, Quarteroni and Veneziani (Reference Formaggia, Quarteroni and Veneziani2009a ), Taylor and Figueroa (Reference Taylor and Figueroa2009) and Quarteroni, Veneziani and Vergara (Reference Quarteroni, Veneziani and Vergara2016c ) for the circulatory system, and Peskin (Reference Peskin2002), Smith et al. (Reference Smith, Nickerson, Crampin and Hunter2004), Colli Franzone, Pavarino and Scacchi (Reference Colli Franzone, Pavarino and Scacchi2014), Quarteroni (Reference Quarteroni2015) and Quarteroni et al. (Reference Quarteroni, Lassila, Rossi and Ruiz-Baier2017) for the heart.
This review paper consists of three main parts: in Part 1 we model the arterial circulation (Sections 2, 3 and 4), in Part 2 we model the heart function (Sections 5, 6 and 7), and in Part 3 we treat inverse problems and include uncertainty (Sections 8, 9, 10 and 11). Both Parts 1 and 2 consist of an introductory section on physiology (Sections 2 and 5), a section describing the available data and their use (Sections 3 and 6), and a final section on mathematical and numerical modelling (Sections 4 and 7). In Part 3 we begin by emphasizing the need to move beyond a single (forward) simulation in some applications (Section 8). This represents the common denominator of three topics recently applied to cardiovascular mathematics: control and optimization (Section 9), parameter estimation (Section 10) and uncertainty quantification (Section 11).
When appropriate (in particular in Sections 4, 7, 9, 10 and 11), we report some numerical results to highlight the effectiveness of the numerical strategies presented here. Unless otherwise specified, all our numerical results have been obtained using the finite element library LifeV; see www.lifev.org for more details.
PART ONE
Arterial circulation
2 Basic facts on quantitative physiology
The cardiovascular system is a closed circuit that carries oxygenated blood to all the tissues and organs of the body. Functionally, it can be regarded as made up of three compartments: the heart, the systemic and pulmonary circulations, and the microvasculature. In this section we will recall the most important features of the physiology of the systemic circulation characterizing the mathematical models that will be introduced later on. We will also highlight the main peculiarities of the pulmonary circulation. Heart physiology will be addressed in Section 5.
The systemic circulation is made up of the arteries, which carry oxygenated blood ejected by the left heart to the living tissues, and the veins, which allow non-oxygenated blood to return to the right heart. The exchange of oxygen between blood and the body tissues occurs in the microvasculature, which in fact separates the systemic arterial tree from the venous systems. In the pulmonary circulation, non-oxygenated blood ejected by the right heart flows in the pulmonary arteries towards the lungs where it becomes oxygenated and goes back to the left heart through the pulmonary veins.
Blood is composed of plasma (about 55% of its total volume), which consists of water (about 92% of plasma volume), proteins and ions. The remainder corresponds to the blood cells, of which 97% of the volume is made up of erythrocytes (red blood cells), which carry the oxygen in oxygenated blood. The other cells are leucocytes (white blood cells) and platelets. The diameter of blood cells is approximately
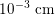 $10^{-3}~\text{cm}$
, whereas that of the smallest arteries and veins is about
$10^{-3}~\text{cm}$
, whereas that of the smallest arteries and veins is about
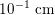 $10^{-1}~\text{cm}$
. This is why blood in the systemic and pulmonary circulations is often considered to be Newtonian, that is, characterized by a linear relationship between internal forces and velocity gradients (Perktold and Hilbert Reference Perktold and Hilbert1986, Formaggia et al.
Reference Formaggia, Quarteroni and Veneziani2009a
). However, in the smallest arteries, such as coronary arteries (the arteries perfusing the heart and the corresponding veins: see Figure 2.1(c)), or in the presence of vessel narrowing (stenosis), non-Newtonian blood rheology is more appropriate: see e.g. Chen, Lu and Wang (Reference Chen, Lu and Wang2006) and references therein.
$10^{-1}~\text{cm}$
. This is why blood in the systemic and pulmonary circulations is often considered to be Newtonian, that is, characterized by a linear relationship between internal forces and velocity gradients (Perktold and Hilbert Reference Perktold and Hilbert1986, Formaggia et al.
Reference Formaggia, Quarteroni and Veneziani2009a
). However, in the smallest arteries, such as coronary arteries (the arteries perfusing the heart and the corresponding veins: see Figure 2.1(c)), or in the presence of vessel narrowing (stenosis), non-Newtonian blood rheology is more appropriate: see e.g. Chen, Lu and Wang (Reference Chen, Lu and Wang2006) and references therein.
Thanks to heart contraction, blood flow is pulsatile, and blood is pumped into the two circulations by means of discrete pulses with a pressure usually varying during a heartbeat in the ranges
![]() $70$
–
$70$
–
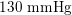 $130~\text{mmHg}$
and
$130~\text{mmHg}$
and
![]() $20$
–
$20$
–
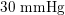 $30~\text{mmHg}$
for the systemic and pulmonary networks, respectively (
$30~\text{mmHg}$
for the systemic and pulmonary networks, respectively (
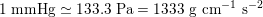 $1~\text{mmHg}\simeq 133.3~\text{Pa}=1333~\text{g}~\text{cm}^{-1}~\text{s}^{-2}$
).
$1~\text{mmHg}\simeq 133.3~\text{Pa}=1333~\text{g}~\text{cm}^{-1}~\text{s}^{-2}$
).
In the systemic circulation, blood first enters the aorta (the largest artery with diameter equal to about
![]() $2.5~\text{cm}$
in adults: see Figure 2.1(a)) and then flows through a network of hundreds of branching arteries of decreasing size, reaching all the regions of the body. Dimensions and numbers of veins are comparable with those of arteries. The waveform of the flow rate as a function of time is characterized by different peak values when moving downstream towards the smallest arteries. In particular, the flow rate peak value is about
$2.5~\text{cm}$
in adults: see Figure 2.1(a)) and then flows through a network of hundreds of branching arteries of decreasing size, reaching all the regions of the body. Dimensions and numbers of veins are comparable with those of arteries. The waveform of the flow rate as a function of time is characterized by different peak values when moving downstream towards the smallest arteries. In particular, the flow rate peak value is about
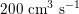 $200~\text{cm}^{3}~\text{s}^{-1}$
in the aorta,
$200~\text{cm}^{3}~\text{s}^{-1}$
in the aorta,
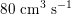 $80~\text{cm}^{3}~\text{s}^{-1}$
in the abdominal aorta,
$80~\text{cm}^{3}~\text{s}^{-1}$
in the abdominal aorta,
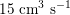 $15~\text{cm}^{3}~\text{s}^{-1}$
in the carotid arteries (the arteries supplying blood to the brain: see Figure 2.1(b)), and
$15~\text{cm}^{3}~\text{s}^{-1}$
in the carotid arteries (the arteries supplying blood to the brain: see Figure 2.1(b)), and
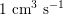 $1~\text{cm}^{3}~\text{s}^{-1}$
in the coronary arteries (corresponding to a maximum blood velocity of about
$1~\text{cm}^{3}~\text{s}^{-1}$
in the coronary arteries (corresponding to a maximum blood velocity of about
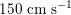 $150~\text{cm}~\text{s}^{-1}$
in the aorta,
$150~\text{cm}~\text{s}^{-1}$
in the aorta,
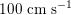 $100~\text{cm}~\text{s}^{-1}$
in the abdominal aorta,
$100~\text{cm}~\text{s}^{-1}$
in the abdominal aorta,
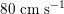 $80~\text{cm}~\text{s}^{-1}$
in the carotid arteries and
$80~\text{cm}~\text{s}^{-1}$
in the carotid arteries and
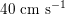 $40~\text{cm}~\text{s}^{-1}$
in the coronary arteries). Further, the shape of the waveforms changes while moving downstream: see Figure 2.2(a). In particular, in the ascending aorta, after the systolic peak the flow rate decelerates assuming null or even negative values, whereas in the abdominal aorta and in carotid arteries it is more spread out and always positive. In any case, we can distinguish the systolic phase – the interval of acceleration and deceleration of blood flow – and the diastolic phase – the interval of almost constant or negative flow.Footnote
1
A different situation occurs in coronary arteries, where the peak flow rate is reached during diastole: see Figure 2.2(b). The coronary arteries are not directly fed by the heart; indeed, blood in the proximal part of the aorta (the sinuses of Valsalva from which the coronary arteries originate) during diastole is allowed to enter the coronary arteries thanks to the elastic response of the aorta (see below for more details).
$40~\text{cm}~\text{s}^{-1}$
in the coronary arteries). Further, the shape of the waveforms changes while moving downstream: see Figure 2.2(a). In particular, in the ascending aorta, after the systolic peak the flow rate decelerates assuming null or even negative values, whereas in the abdominal aorta and in carotid arteries it is more spread out and always positive. In any case, we can distinguish the systolic phase – the interval of acceleration and deceleration of blood flow – and the diastolic phase – the interval of almost constant or negative flow.Footnote
1
A different situation occurs in coronary arteries, where the peak flow rate is reached during diastole: see Figure 2.2(b). The coronary arteries are not directly fed by the heart; indeed, blood in the proximal part of the aorta (the sinuses of Valsalva from which the coronary arteries originate) during diastole is allowed to enter the coronary arteries thanks to the elastic response of the aorta (see below for more details).

Figure 2.1. The aorta (a), the carotid arteries (b) and (a subset of) the coronary arteries (c).
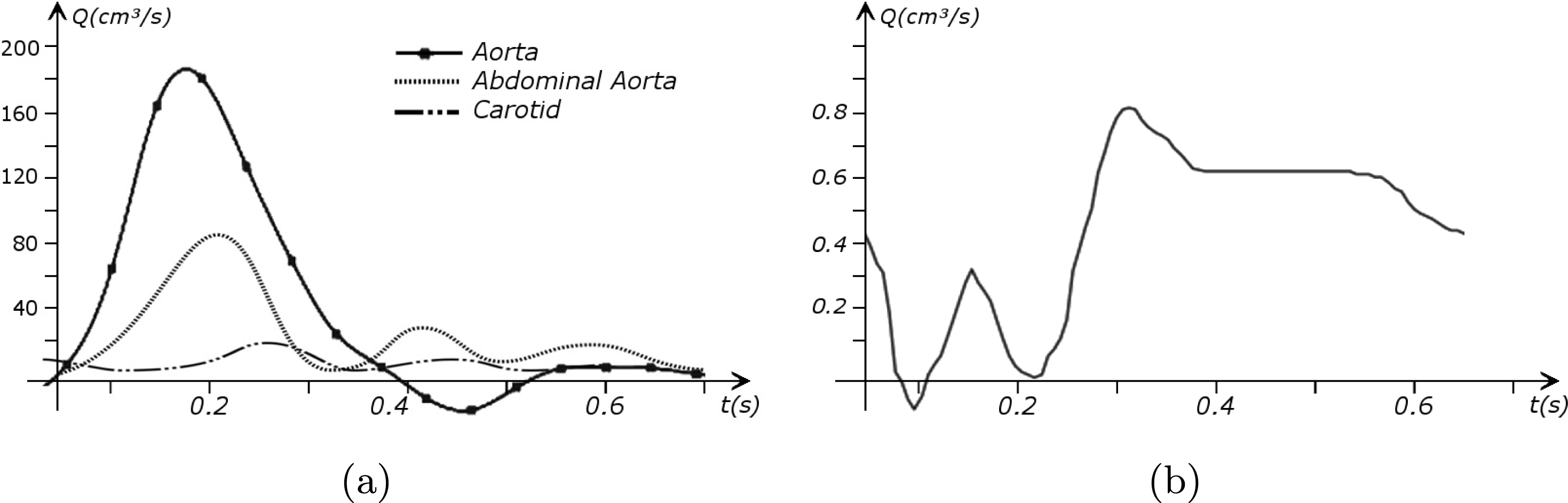
Figure 2.2. Typical flow rate waveforms in the ascending aorta, abdominal aorta and carotid arteries (a), and in the coronary arteries (b).
In the pulmonary circulation blood first enters the pulmonary artery (diameter equal to about
![]() $3.0~\text{cm}$
in adults) and then flows into another network of branching arteries of decreasing size reaching the lungs. The waveforms and peak intensities are similar to those of the systemic arteries.
$3.0~\text{cm}$
in adults) and then flows into another network of branching arteries of decreasing size reaching the lungs. The waveforms and peak intensities are similar to those of the systemic arteries.
The different characteristics of blood flow in the arteries of the systemic circulation result in different values of the Reynolds number
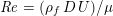 $\mathit{Re}=(\unicode[STIX]{x1D70C}_{f}\,D\,U)/\unicode[STIX]{x1D707}$
(where
$\mathit{Re}=(\unicode[STIX]{x1D70C}_{f}\,D\,U)/\unicode[STIX]{x1D707}$
(where
![]() $\unicode[STIX]{x1D70C}_{f}$
is the blood density,
$\unicode[STIX]{x1D70C}_{f}$
is the blood density,
![]() $D$
and
$D$
and
![]() $U$
are the characteristic vessel dimension and blood velocity, respectively, and
$U$
are the characteristic vessel dimension and blood velocity, respectively, and
![]() $\unicode[STIX]{x1D707}$
is the fluid viscosity), a dimensionless number which quantifies the importance of inertial forces over the viscous forces. In particular,
$\unicode[STIX]{x1D707}$
is the fluid viscosity), a dimensionless number which quantifies the importance of inertial forces over the viscous forces. In particular,
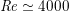 $\mathit{Re}\simeq 4000$
in the aorta and
$\mathit{Re}\simeq 4000$
in the aorta and
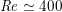 $\mathit{Re}\simeq 400$
in coronary arteries, with intermediate values when moving downstream along the aorta. Thus, blood covers a range of Reynolds numbers where both the inertial and the viscous components of the flow are relevant. Although in the aorta
$\mathit{Re}\simeq 400$
in coronary arteries, with intermediate values when moving downstream along the aorta. Thus, blood covers a range of Reynolds numbers where both the inertial and the viscous components of the flow are relevant. Although in the aorta
![]() $\mathit{Re}$
is higher than the critical value of
$\mathit{Re}$
is higher than the critical value of
![]() $2000$
above which the flow would no longer be laminar in a straight pipe, the pulsatile nature of blood flow does not allow development of full transition to turbulence. It is debatable whether transition to turbulence effects occur in the aorta. Some authors speculate that the helicoidal velocity pattern in the aorta, induced by the torsion of the heart’s contraction, inhibits any transition to turbulence, thus supporting the thesis that in healthy conditions turbulence is never observed in the cardiovascular system (Morbiducci et al.
Reference Morbiducci, Ponzini, Rizzo, Cadioli, Esposito, De Cobelli, Del Maschio, Montevecchi and Redaelli2009). This is not necessarily the case for some pathological conditions, such as carotid stenosis, yielding a narrowing of the vessel lumen and increased complexity of the geometry together with higher Reynolds numbers: see e.g. Ahmed and Giddens (Reference Ahmed and Giddens1984), Lee et al. (Reference Lee, Lee, Fischer, Bassiouny and Loth2008), Kefayati, Holdsworth and Poepping (Reference Kefayati, Holdsworth and Poepping2014) and Lancellotti et al. (Reference Lancellotti, Vergara, Valdettaro, Bose and Quarteroni2015). The Womersley number
$2000$
above which the flow would no longer be laminar in a straight pipe, the pulsatile nature of blood flow does not allow development of full transition to turbulence. It is debatable whether transition to turbulence effects occur in the aorta. Some authors speculate that the helicoidal velocity pattern in the aorta, induced by the torsion of the heart’s contraction, inhibits any transition to turbulence, thus supporting the thesis that in healthy conditions turbulence is never observed in the cardiovascular system (Morbiducci et al.
Reference Morbiducci, Ponzini, Rizzo, Cadioli, Esposito, De Cobelli, Del Maschio, Montevecchi and Redaelli2009). This is not necessarily the case for some pathological conditions, such as carotid stenosis, yielding a narrowing of the vessel lumen and increased complexity of the geometry together with higher Reynolds numbers: see e.g. Ahmed and Giddens (Reference Ahmed and Giddens1984), Lee et al. (Reference Lee, Lee, Fischer, Bassiouny and Loth2008), Kefayati, Holdsworth and Poepping (Reference Kefayati, Holdsworth and Poepping2014) and Lancellotti et al. (Reference Lancellotti, Vergara, Valdettaro, Bose and Quarteroni2015). The Womersley number
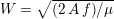 $W=\sqrt{(2\,A\,f)/\unicode[STIX]{x1D707}}$
(where
$W=\sqrt{(2\,A\,f)/\unicode[STIX]{x1D707}}$
(where
![]() $A$
and
$A$
and
![]() $f$
are the characteristic cross-section vessel area and time frequency of the flow rate signal, respectively) is a dimensionless number quantifying the pulsatility of flow. We find decreasing values in the systemic circulation moving downstream:
$f$
are the characteristic cross-section vessel area and time frequency of the flow rate signal, respectively) is a dimensionless number quantifying the pulsatility of flow. We find decreasing values in the systemic circulation moving downstream:
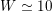 $W\simeq 10$
in the aorta,
$W\simeq 10$
in the aorta,
![]() $W\simeq 3$
in the carotid arteries. Similar values of
$W\simeq 3$
in the carotid arteries. Similar values of
![]() $\mathit{Re}$
and
$\mathit{Re}$
and
![]() $W$
are found in the pulmonary arteries.
$W$
are found in the pulmonary arteries.
In the veins of the systemic circulation, we find values of the flow rate, Reynolds and Womersley numbers comparable to the arteries, the only difference being that the blood flow waveform is more spread out than for the corresponding arteries. Another major difference is given by blood pressure values. In the arteries the range of pressure is almost the same, independent of the location in the tree (
![]() $70$
–
$70$
–
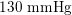 $130~\text{mmHg}$
), whereas in the veins it reduces, assuming a mean value of about
$130~\text{mmHg}$
), whereas in the veins it reduces, assuming a mean value of about
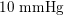 $10~\text{mmHg}$
. This is due to the high resistance experienced by blood flow in the microvasculature. The latter is composed of thousands of arterioles and venules and billions of capillaries. The blood velocity and vessel dimensions are here greatly reduced (about
$10~\text{mmHg}$
. This is due to the high resistance experienced by blood flow in the microvasculature. The latter is composed of thousands of arterioles and venules and billions of capillaries. The blood velocity and vessel dimensions are here greatly reduced (about
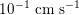 $10^{-1}~\text{cm}~\text{s}^{-1}$
in the former and
$10^{-1}~\text{cm}~\text{s}^{-1}$
in the former and
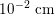 $10^{-2}~\text{cm}$
in the latter). This means that
$10^{-2}~\text{cm}$
in the latter). This means that
![]() $\mathit{Re}$
is very small in comparison with the systemic circulation, so viscous forces completely dominate the inertial forces. As a result, the highest resistance to flow is found in the microvasculature, thus provoking a big decrease in the blood pressure. Since the typical dimension of capillaries is comparable to that of erythrocytes, a multiphase model seems appropriate for their mathematical description (Enden and Popel Reference Enden and Popel1992). Finally, we observe that most veins are supplied with valves that prevent backflow of blood, and venous flow is highly sensitive to muscle contraction and respiratory effects.
$\mathit{Re}$
is very small in comparison with the systemic circulation, so viscous forces completely dominate the inertial forces. As a result, the highest resistance to flow is found in the microvasculature, thus provoking a big decrease in the blood pressure. Since the typical dimension of capillaries is comparable to that of erythrocytes, a multiphase model seems appropriate for their mathematical description (Enden and Popel Reference Enden and Popel1992). Finally, we observe that most veins are supplied with valves that prevent backflow of blood, and venous flow is highly sensitive to muscle contraction and respiratory effects.
As observed, blood pressure assumes the same range of values along the entire systemic arterial tree,
![]() $70$
–
$70$
–
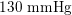 $130~\text{mmHg}$
. More precisely, negligible dissipation is experienced by the pressure signal in large and medium sized vessels before reaching the small vessels and microvasculature. Of course, at a given instant the pressure is not constant in space along the tree. Indeed, a time shift characterizes the pressure waveforms at different locations which generate gradient pressures between proximal and distal regions facilitating blood movement. These spatial gradients are due to the propagating nature of the pressure, which is in fact a wave travelling along the arterial network. The wave speed ranges from about
$130~\text{mmHg}$
. More precisely, negligible dissipation is experienced by the pressure signal in large and medium sized vessels before reaching the small vessels and microvasculature. Of course, at a given instant the pressure is not constant in space along the tree. Indeed, a time shift characterizes the pressure waveforms at different locations which generate gradient pressures between proximal and distal regions facilitating blood movement. These spatial gradients are due to the propagating nature of the pressure, which is in fact a wave travelling along the arterial network. The wave speed ranges from about
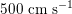 $500~\text{cm}~\text{s}^{-1}$
in the aorta to
$500~\text{cm}~\text{s}^{-1}$
in the aorta to
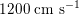 $1200~\text{cm}~\text{s}^{-1}$
in the coronary arteries. The presence of bifurcations or high-resistance regions, such as the microvasculature, produces wave reflections that propagate back towards the heart.
$1200~\text{cm}~\text{s}^{-1}$
in the coronary arteries. The presence of bifurcations or high-resistance regions, such as the microvasculature, produces wave reflections that propagate back towards the heart.
The propagation of a pressure wave along the vascular tree is due to vessel compliance, that is, the ability of the vessel to distend under the forces exerted by blood pressure. Vessel wall displacements are quite large, reaching up to 10% of the lumen diameter. This is possible thanks to the structure of the vessel walls: their total thickness is about 10% of the lumen diameter and they are composed of three layers: the intima, the media and the adventitia. The inner part of the intima is the endothelium (facing the blood), whereas the remaining part is made up of connective tissue. The media and the adventitia play a major role in characterizing the mechanical response of the vessel wall. Their main structural components are elastin and collagen. The media is also formed of smooth muscle cells which provide tone to the vessel wall. Elastin forms complex networks that are very distensible, providing the elasticity of the vessel wall at small strain. In contrast, collagen forms stiff fibres oriented in a helical form providing tensile strength at large strain. Thus, the artery vessel wall is characterized by highly non-linear elastic properties. The quantity of elastin and collagen decreases going downstream along the arterial network, whereas the quantity of smooth muscle cells increases. This allows the proximal arteries (to the heart), in particular the aorta, to be very extensible and, thanks to the high peripheral resistances due to the elevated tone of the distal arteries and to the microvasculature, to store about 50% of the blood entering during systole. This blood reserve is then discharged during diastole owing to the vessel wall elastic response (the windkessel effect). This is responsible for the smoothing of the blood flow waveform discussed above, going downstream along the arterial network, which guarantees nearly continuous peripheral blood flow and thus an almost continuous exchange of oxygen with the tissues. Further, pulmonary artery walls are extensible (with muscular tone increasing downstream), even though their thickness is only about 1% of the lumen diameter.
As already observed, there is mutual exchange of energy between blood and extensible vessel walls: the latter accumulate elastic potential energy under the forces exerted by the blood pressure, which is then transferred to the blood as kinetic energy. From the mechanical point of view, this gives rise to a fluid–structure interaction problem. This process occurs at short time scales, proportional to the duration of a heartbeat (
![]() ${\sim}\,$
1 s). Other interaction mechanisms may take place at larger time scales yielding wall modifications of vessel properties. This occurs in the case of several arterial diseases, such as atherosclerosis and aneurysm formation. In the first case, an increased permeability of vessel wall to lipoprotein provokes a cascade of events at the cellular level which leads to the accumulation of fatty material in the intima, just below the endothelium, and then to plaque formation in the media. Preferential sites of atherosclerotic plaque formation are the carotid arteries and the coronary arteries. The main complications are partial occlusion of the lumen with consequent (cerebral or cardiac) ischaemia, or even total occlusion resulting in (cerebral or cardiac) infarction. An aneurysm consists in the dilatation of the vessel wall with formation of a (possibly huge) bulge, mainly in the aorta and cerebral arteries, due to a loss of elastin and to the consequent remodelling of collagen, resulting in a weakening of the arterial wall; 80–90% of ruptured abdominal aortic aneurysms and 45% of ruptured cerebral aneurysms result in death. The role of blood fluid dynamics has been recognized as crucial for the development of both of these diseases (Glagov et al.
Reference Glagov, Zarins, Giddens and Ku1988, Bagci et al.
Reference Bagci, Vodovotz, Billiar, Ermentrout and Bahar2008). In particular, wall shear stresses, that is, the viscous/friction forces exerted by the blood on the endothelium, despite being 100 times smaller in magnitude than pressure, regulate the permeability of the wall to lipoprotein and the loss of elastin, thus playing an important role in atherosclerosis and aneurysm development. For both these arterial diseases, this supplementary interaction between fluid and structure occurs at time scales of several years.
${\sim}\,$
1 s). Other interaction mechanisms may take place at larger time scales yielding wall modifications of vessel properties. This occurs in the case of several arterial diseases, such as atherosclerosis and aneurysm formation. In the first case, an increased permeability of vessel wall to lipoprotein provokes a cascade of events at the cellular level which leads to the accumulation of fatty material in the intima, just below the endothelium, and then to plaque formation in the media. Preferential sites of atherosclerotic plaque formation are the carotid arteries and the coronary arteries. The main complications are partial occlusion of the lumen with consequent (cerebral or cardiac) ischaemia, or even total occlusion resulting in (cerebral or cardiac) infarction. An aneurysm consists in the dilatation of the vessel wall with formation of a (possibly huge) bulge, mainly in the aorta and cerebral arteries, due to a loss of elastin and to the consequent remodelling of collagen, resulting in a weakening of the arterial wall; 80–90% of ruptured abdominal aortic aneurysms and 45% of ruptured cerebral aneurysms result in death. The role of blood fluid dynamics has been recognized as crucial for the development of both of these diseases (Glagov et al.
Reference Glagov, Zarins, Giddens and Ku1988, Bagci et al.
Reference Bagci, Vodovotz, Billiar, Ermentrout and Bahar2008). In particular, wall shear stresses, that is, the viscous/friction forces exerted by the blood on the endothelium, despite being 100 times smaller in magnitude than pressure, regulate the permeability of the wall to lipoprotein and the loss of elastin, thus playing an important role in atherosclerosis and aneurysm development. For both these arterial diseases, this supplementary interaction between fluid and structure occurs at time scales of several years.
More on the physiology of the systemic and pulmonary circulations and microvasculature in view of mathematical modelling is available in Nichols and O’Rourke (Reference Nichols and O’Rourke2005), Quarteroni, Tuveri and Veneziani (Reference Quarteroni, Tuveri and Veneziani2000c ) and Formaggia et al. (Reference Formaggia, Quarteroni and Veneziani2009a ), for example.
3 All about data
The ultimate ambition of mathematical models in medicine is to provide quantitative results to enhance the understanding of biophysical processes and hence to support clinicians in their diagnostic and therapeutic procedures. To this end, we must consider data that are patient-specific, to use the bioengineering jargon – that is, related to real patients. Obtaining and processing patient-specific data is a major issue which deserves a specific review paper in its own right. Here, we provide a brief overview of the most common techniques for acquisition and analysis of ‘clinical’ data. This data preprocessing is essential prior to the set-up of a numerical simulation.
In this section we address the case of data related to the arterial (or venous) circulation, whereas in Section 6 we will discuss cardiac data. In arteries we have two interacting processes: the blood flow in the vessel lumen (the region occupied by the blood, which is referred to as the fluid domain) and the displacement of the vessel wall (referred to as structure). We need geometric, boundary and biological data, which are discussed below.
3.1 Geometric vascular data
Geometric data are necessary to build the geometry of the computational domains wherein the differential problems are numerically solved. At the end of the geometric preprocessing step, we obtain the fluid computational domain for the blood fluid dynamics problem, and the structure computational domain for the vessel wall displacement problem.
The processing of geometric data for blood flow simulations is a major task since vessels exhibit high morphological variability due, for example, to the evident vessel tortuosity and the presence of several bifurcations. Moreover, in unhealthy cases, this variability is further emphasized, because of the possible presence of calcifications, stenoses, aneurysms or even prostheses (such as stents).
Geometric preprocessing consists of the following steps, which are usually performed in sequence (Antiga et al. Reference Antiga, Piccinelli, Botti, Ene-Iordache, Remuzzi and Steinman2008, Antiga, Peiró and Steinman Reference Antiga, Peiró, Steinman, Formaggia, Quarteroni and Veneziani2009): acquisition of clinical images, image enhancement, image segmentation, and generation of the computational mesh. These items are addressed below.
3.1.1 Acquisition of clinical images
Angiography is an imaging technique successfully used to ‘identify’ the vessel lumen. It exploits the property that a liquid inside the vessel appears brighter than the vessel wall and the surrounding tissue. Angiographies are usually acquired as two-dimensional (2D) images, corresponding to different slices of the domain of interest, but three-dimensional (3D) acquisitions of volumes are also possible.
One of the most common techniques for obtaining an angiography is X-ray imaging, based on the projection of X-ray beams through the body onto suitable screens, and on the contrast produced in the 2D image by the different absorption properties of body structures. To highlight the vessel lumen, a radio-opaque dye is inserted into the bloodstream through the arterial system. To reconstruct tortuous geometries, a rotational angiography (RA) is performed, where X-ray sources and detectors are rapidly rotated around the patient, allowing one to acquire many projections within a few seconds. The excellent spatial resolution of projection angiography (about
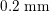 $0.2~\text{mm}$
,
$0.2~\text{mm}$
,
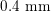 $0.4~\text{mm}$
for RA) makes this technique the gold standard for most vascular imaging applications. Another X-ray angiography technique, widely used for blood flow simulation, is based on computed tomography (CT) technology, where multiple X-ray sources and detectors are rotated rapidly around the patient, allowing one to acquire 3D images with excellent spatial resolution (less than
$0.4~\text{mm}$
for RA) makes this technique the gold standard for most vascular imaging applications. Another X-ray angiography technique, widely used for blood flow simulation, is based on computed tomography (CT) technology, where multiple X-ray sources and detectors are rotated rapidly around the patient, allowing one to acquire 3D images with excellent spatial resolution (less than
![]() $1~\text{mm}$
in computed tomography angiography, CTA). Unlike projection angiography, another advantage of CTA is the possibility of using intravenous rather than arterial injections. Recently, temporally resolved CTA (4D-CTA) has become feasible. This allows one to obtain several (15–20) 3D images during a heartbeat.
$1~\text{mm}$
in computed tomography angiography, CTA). Unlike projection angiography, another advantage of CTA is the possibility of using intravenous rather than arterial injections. Recently, temporally resolved CTA (4D-CTA) has become feasible. This allows one to obtain several (15–20) 3D images during a heartbeat.
Difficulties may arise in the presence of metal artifacts due to metallic prostheses such as pacemakers, resulting in streaks on the images obscuring anatomical details; see Robertson et al. (Reference Robertson, Yuan, Wang and Vannier1997) and Faggiano, Lorenzi and Quarteroni (Reference Faggiano, Lorenzi and Quarteroni2014) for possible mathematical treatments.
Another widely used technique to obtain angiographies is magnetic resonance imaging (MRI), based on the different decay rates exhibited by body structures on exposure to radio frequency (RF) energy. This is called magnetic resonance angiography (MRA). The generated contrast in the images can be tuned by selecting different RF stimuli. This allows MRA to be suitably tuned to detect soft tissues. Another advantage of MRA is that angiography can be generated without using exogenous agents. However, usually an intravenous injection of a paramagnetic contrast agent is used to improve the blood signal and reduce the acquisition time (contrast-enhanced (CE)-MRA).
Finally, we mention ultrasound (US) imaging, based on the reflections of high-frequency sound waves (a few MHz) transmitted into the body. Ultrasound is the least expensive and invasive of the techniques discussed here, and allows real-time acquisition of 2D images. In contrast, its spatial resolution is the poorest. Recently it has even been possible to acquire 3D images (3D US) by reconstructing a 3D volume from 2D slices.
On the other hand, only a few techniques currently allow us to obtain images of vessel walls. Among these we cite black blood (BB)-MRA, by which the vessel wall and the surrounding tissue can also be viewed, and intravascular ultrasound (IVUS), which is however very invasive since the transducer is placed directly into the artery (typically a coronary artery) via a catheter.
No matter which technique is used, from a mathematical standpoint we can assume that at the end of the acquisition step we obtain a vector
![]() $\boldsymbol{I}^{\mathit{clin}}$
, whose
$\boldsymbol{I}^{\mathit{clin}}$
, whose
![]() $j$
th component,
$j$
th component,
![]() $I_{j}^{\mathit{clin}}$
, corresponds to the intensity of the image at the point
$I_{j}^{\mathit{clin}}$
, corresponds to the intensity of the image at the point
![]() $\boldsymbol{x}_{j}$
in grey-scale representing the contrast generated by the imaging technique. The collection of the points
$\boldsymbol{x}_{j}$
in grey-scale representing the contrast generated by the imaging technique. The collection of the points
![]() $\boldsymbol{x}_{j}$
,
$\boldsymbol{x}_{j}$
,
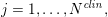 $j=1,\ldots ,N^{\mathit{clin}},$
forms the lattice
$j=1,\ldots ,N^{\mathit{clin}},$
forms the lattice
![]() ${\mathcal{L}}^{\mathit{clin}}$
, where
${\mathcal{L}}^{\mathit{clin}}$
, where
![]() $N^{\mathit{clin}}$
is the total number of acquisition points (pixels or voxels) where the image contrast has been evaluated. Here and below, a lattice is a simple collection of points determined by the point coordinates. It can be useful to associate a corresponding image intensity (scalar) function with the image intensity vector
$N^{\mathit{clin}}$
is the total number of acquisition points (pixels or voxels) where the image contrast has been evaluated. Here and below, a lattice is a simple collection of points determined by the point coordinates. It can be useful to associate a corresponding image intensity (scalar) function with the image intensity vector
![]() $\boldsymbol{I}^{\mathit{clin}}$
, which is typically obtained by interpolation, and will be denoted by
$\boldsymbol{I}^{\mathit{clin}}$
, which is typically obtained by interpolation, and will be denoted by
![]() $I^{\mathit{clin}}(\boldsymbol{x})$
.
$I^{\mathit{clin}}(\boldsymbol{x})$
.
3.1.2 Image enhancement
Medical images are often affected by noise and artifacts that may interfere with the quality of the final results of the preprocessing step. Thus, prior to the reconstruction of the 3D geometry, an imaging enhancement is usually performed.
One popular enhancement technique is resampling, consisting in suitably changing the resolution of the images in one or more directions. In practice, an interpolation of image intensity values
![]() $\boldsymbol{I}^{\mathit{clin}}$
onto a more refined lattice is performed. The most commonly used methods are constant interpolation, first-order composite Lagrangian interpolation, B-spline (Unser Reference Unser1999), and windowed sinc interpolation.
$\boldsymbol{I}^{\mathit{clin}}$
onto a more refined lattice is performed. The most commonly used methods are constant interpolation, first-order composite Lagrangian interpolation, B-spline (Unser Reference Unser1999), and windowed sinc interpolation.
The noise in the medical images may be due to thermal effects in the signal processing electronics or to other undesired sources. Reduction of noise could be obtained by means of a smoothing filter, which does not require any prior information about the nature of the noise and has a regularizing effect on the image. This technique is the most commonly used both for CT and MRI images. A very popular filter is the Gaussian filter, consisting in performing a discrete convolution with a Gaussian kernel over the lattice
![]() ${\mathcal{L}}^{\mathit{clin}}$
of the image intensity
${\mathcal{L}}^{\mathit{clin}}$
of the image intensity
![]() $\boldsymbol{I}^{\mathit{clin}}$
. Unfortunately, together with the noise, smoothing could also filter significant high-frequency image contents. Moreover, since the image is separated from the background by sharp boundaries, characterized by high-frequency content, the smoothing filter could blur and move the boundaries. To prevent this, anisotropic diffusion filtering has been introduced (Perona and Malik Reference Perona and Malik1990): the heat equation is solved for a new image intensity function, with diffusion coefficient decreasing for increasing values of the gradient magnitude of intensity. By so doing, the filtering is not performed at the boundaries where the gradient is large.
$\boldsymbol{I}^{\mathit{clin}}$
. Unfortunately, together with the noise, smoothing could also filter significant high-frequency image contents. Moreover, since the image is separated from the background by sharp boundaries, characterized by high-frequency content, the smoothing filter could blur and move the boundaries. To prevent this, anisotropic diffusion filtering has been introduced (Perona and Malik Reference Perona and Malik1990): the heat equation is solved for a new image intensity function, with diffusion coefficient decreasing for increasing values of the gradient magnitude of intensity. By so doing, the filtering is not performed at the boundaries where the gradient is large.
Another technique, called multiscale vessel enhancement (Frangi et al.
Reference Frangi, Niessen, Hoogeveen, van Walsum and Viergever1999), exploits the specific tubular shape of vascular geometries, and therefore assumes that the minimum modulus eigenvalue of the Hessian matrix of the image intensity function
![]() $I^{\mathit{clin}}$
is small, while the other two are large and of equal sign.
$I^{\mathit{clin}}$
is small, while the other two are large and of equal sign.
At the end of this substep we obtain a new image intensity vector
![]() $\boldsymbol{I}^{\mathit{en}}$
whose
$\boldsymbol{I}^{\mathit{en}}$
whose
![]() $j$
th component,
$j$
th component,
![]() $I_{j}^{\mathit{en}}$
, denotes the intensity of the enhanced image in grey-scale at the point
$I_{j}^{\mathit{en}}$
, denotes the intensity of the enhanced image in grey-scale at the point
![]() $\boldsymbol{x}_{j}$
,
$\boldsymbol{x}_{j}$
,
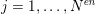 $j=1,\ldots ,N^{\mathit{en}}$
, in the lattice
$j=1,\ldots ,N^{\mathit{en}}$
, in the lattice
![]() ${\mathcal{L}}^{\mathit{en}}$
(and correspondingly an associated enhanced image intensity function
${\mathcal{L}}^{\mathit{en}}$
(and correspondingly an associated enhanced image intensity function
![]() $I^{\mathit{en}}(\boldsymbol{x})$
via interpolation). Here,
$I^{\mathit{en}}(\boldsymbol{x})$
via interpolation). Here,
![]() $N^{\mathit{en}}$
is the total number of points in the enhanced image intensity vector. Usually,
$N^{\mathit{en}}$
is the total number of points in the enhanced image intensity vector. Usually,
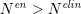 $N^{\mathit{en}}>N^{\mathit{clin}}$
.
$N^{\mathit{en}}>N^{\mathit{clin}}$
.
3.1.3 Image segmentation
Image segmentation is the cornerstone of the preprocessing step. It consists in the construction of the shape of a vascular district from the image obtained after the enhancement substep. In particular, the segmentation allows one to detect those points of the lattice
![]() ${\mathcal{L}}^{\mathit{en}}$
which – presumably – belong to the boundary of the vessel lumen. The precise definition of the boundary of the lumen is a challenging task which generally requires considerable experience on the part of the user.
${\mathcal{L}}^{\mathit{en}}$
which – presumably – belong to the boundary of the vessel lumen. The precise definition of the boundary of the lumen is a challenging task which generally requires considerable experience on the part of the user.
The first technique we describe is thresholding, consisting in selecting a threshold
![]() $k$
to identify the points
$k$
to identify the points
 $\boldsymbol{x}_{j}\in {\mathcal{L}}^{\mathit{en}}$
such that
$\boldsymbol{x}_{j}\in {\mathcal{L}}^{\mathit{en}}$
such that
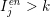 $I_{j}^{\mathit{en}}>k$
. This is motivated by the assumption that
$I_{j}^{\mathit{en}}>k$
. This is motivated by the assumption that
![]() $k$
separates different anatomical structures, in our case the vessel lumen (characterized by intensity values larger than
$k$
separates different anatomical structures, in our case the vessel lumen (characterized by intensity values larger than
![]() $k$
) and the background, obtained by the collection of points for which
$k$
) and the background, obtained by the collection of points for which
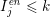 $I_{j}^{\mathit{en}}\leq k$
. The value of
$I_{j}^{\mathit{en}}\leq k$
. The value of
![]() $k$
is determined either manually or via a suitable algorithm. In the latter case, one commonly used strategy is full width at half maximum (FWHM), consisting in setting the threshold halfway between the peak intensity within the lumen and the intensity of the background. For the segmentation of special structures, such as calcifications or stents, higher-bound thresholds are used (Boldak, Rolland and Toumoulin Reference Boldak, Rolland and Toumoulin2003).
$k$
is determined either manually or via a suitable algorithm. In the latter case, one commonly used strategy is full width at half maximum (FWHM), consisting in setting the threshold halfway between the peak intensity within the lumen and the intensity of the background. For the segmentation of special structures, such as calcifications or stents, higher-bound thresholds are used (Boldak, Rolland and Toumoulin Reference Boldak, Rolland and Toumoulin2003).
A more sophisticated class of segmentation methods than thresholding is given by front propagation methods, where the propagation of a suitable wavefront is tracked. The speed of the wave is small in regions where
![]() $\boldsymbol{I}^{\mathit{en}}$
changes rapidly and high for other regions, so the wavefront slows down when approaching the boundary. The most popular front propagation method is the fast marching method, which provides an efficient solution to the eikonal problem
$\boldsymbol{I}^{\mathit{en}}$
changes rapidly and high for other regions, so the wavefront slows down when approaching the boundary. The most popular front propagation method is the fast marching method, which provides an efficient solution to the eikonal problem
 $$\begin{eqnarray}\Vert \unicode[STIX]{x1D6FB}T(\boldsymbol{x})\Vert =\frac{1}{V(I^{\mathit{en}}(\boldsymbol{x}))},\quad \boldsymbol{x}\in {\mathcal{D}}^{\mathit{en}},\end{eqnarray}$$
$$\begin{eqnarray}\Vert \unicode[STIX]{x1D6FB}T(\boldsymbol{x})\Vert =\frac{1}{V(I^{\mathit{en}}(\boldsymbol{x}))},\quad \boldsymbol{x}\in {\mathcal{D}}^{\mathit{en}},\end{eqnarray}$$
where
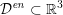 ${\mathcal{D}}^{\mathit{en}}\subset \mathbb{R}^{3}$
is a region that contains all
${\mathcal{D}}^{\mathit{en}}\subset \mathbb{R}^{3}$
is a region that contains all
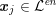 $\boldsymbol{x}_{j}\in {\mathcal{L}}^{\mathit{en}}$
, and where suitable boundary conditions are prescribed on a selected boundary where the propagation starts (Zhu and Tian Reference Zhu and Tian2003). In the above equation,
$\boldsymbol{x}_{j}\in {\mathcal{L}}^{\mathit{en}}$
, and where suitable boundary conditions are prescribed on a selected boundary where the propagation starts (Zhu and Tian Reference Zhu and Tian2003). In the above equation,
![]() $V$
is the speed of the wavefront and
$V$
is the speed of the wavefront and
![]() $T(\boldsymbol{x})$
is the first arrival time at point
$T(\boldsymbol{x})$
is the first arrival time at point
![]() $\boldsymbol{x}$
. In fact,
$\boldsymbol{x}$
. In fact,
![]() $T$
consists of isocontours, denoting a collection of surfaces describing the shape of the waveform. The vessel boundary is then represented by the points
$T$
consists of isocontours, denoting a collection of surfaces describing the shape of the waveform. The vessel boundary is then represented by the points
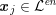 $\boldsymbol{x}_{j}\in {\mathcal{L}}^{\mathit{en}}$
such that
$\boldsymbol{x}_{j}\in {\mathcal{L}}^{\mathit{en}}$
such that
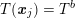 $T(\boldsymbol{x}_{j})=T^{b}$
(up to a given tolerance), where
$T(\boldsymbol{x}_{j})=T^{b}$
(up to a given tolerance), where
![]() $T^{b}$
is a suitable value selected by the user.
$T^{b}$
is a suitable value selected by the user.
Another class of segmentation methods is that of deformable models, where a suitable energy is minimized, allowing the deformation of the body (in our case the boundary of the vessel lumen) to reach a final state with smallest energy, accounting for external terms derived from the image and internal terms constraining the boundary to be regular. The most widely used class of deformable models is the level set method, where a deformable surface is represented implicitly as the zero level of a higher-dimensional embedding function (Sethian Reference Sethian1999). Deformable models, for example those based on cylindrically parametrized surface meshes, incorporate anatomical knowledge of the vessel shape (Frangi et al. Reference Frangi, Niessen, Hoogeveen, van Walsum and Viergever1999, Yim et al. Reference Yim, Cebral, Mullick, Marcos and Choyke2001).
For the segmentation of the vessel wall, Steinman et al. (Reference Steinman, Thomas, Ladak, Milner, Rutt and Spence2001), starting from BB-MRA images, segmented the vessel wall outer boundary using the same deformable model as used for the vessel lumen segmentation. Usually, BB-MRA or other images detecting the vessel wall are not routinely acquired in clinical practice. In this case, a reasonable approach to obtaining the vessel wall is to ‘extrude’ the reconstructed boundary lumen along the outward unit vector by using a suitable function specifying the vessel wall thickness in the different regions of the district of interest.
In those cases where the image intensity vectors
![]() $\boldsymbol{I}^{\mathit{clin}}$
and
$\boldsymbol{I}^{\mathit{clin}}$
and
![]() $\boldsymbol{I}^{\mathit{en}}$
refer to 2D slices, application of the above segmentation strategies leads to identification of several vessel boundaries (contours), one for each slice, which now need to be connected to obtain the 3D boundary surface. This operation is called surface reconstruction. A simple procedure is to connect successive contours with straight lines defining surface triangle edges. This strategy is not suitable in the presence of changes of shape such as in bifurcations. Better surface reconstruction is provided by least-squares fitting of polynomial surfaces to the contour set (Wang, Dutton and Taylor Reference Wang, Dutton and Taylor1999). This strategy is suited to managing bifurcations whose branches are fitted separately with a successive extension into the parent vessel. A variant of this approach has been proposed in Geiger (Reference Geiger1993), where contours are first filled with triangles which are then connected to the triangles of the adjacent contours by means of tetrahedra. The final lumen surface is then represented by the boundary of this tetrahedral mesh (formed by triangles). We also mention shape-based interpolation where, for each contour, a characteristic function with positive (resp. negative) values for points located inside (resp. outside) the contour is constructed. The final lumen boundary surface is then represented by the zero level set of the interpolation of all these characteristic functions (Raya and Udupa Reference Raya and Udupa1990). Finally, we briefly describe interpolation by means of radial basis functions (RBFs), which provide a flexible way of interpolating data in multi-dimensional spaces, even for unstructured data where interpolation nodes are scattered and/or do not form a regular grid, and for which it is often impossible to apply polynomial or spline interpolation (Carr, Fright and Beatson Reference Carr, Fright and Beatson1997, Fornefett, Rohr and Stiehl Reference Fornefett, Rohr and Stiehl2001). The coefficients in the linear combination with respect to the RBF basis are determined by solving a suitable linear system, which is invertible under very mild conditions (Peiró et al.
Reference Peiró, Formaggia, Gazzola, Radaelli and Rigamonti2007).
$\boldsymbol{I}^{\mathit{en}}$
refer to 2D slices, application of the above segmentation strategies leads to identification of several vessel boundaries (contours), one for each slice, which now need to be connected to obtain the 3D boundary surface. This operation is called surface reconstruction. A simple procedure is to connect successive contours with straight lines defining surface triangle edges. This strategy is not suitable in the presence of changes of shape such as in bifurcations. Better surface reconstruction is provided by least-squares fitting of polynomial surfaces to the contour set (Wang, Dutton and Taylor Reference Wang, Dutton and Taylor1999). This strategy is suited to managing bifurcations whose branches are fitted separately with a successive extension into the parent vessel. A variant of this approach has been proposed in Geiger (Reference Geiger1993), where contours are first filled with triangles which are then connected to the triangles of the adjacent contours by means of tetrahedra. The final lumen surface is then represented by the boundary of this tetrahedral mesh (formed by triangles). We also mention shape-based interpolation where, for each contour, a characteristic function with positive (resp. negative) values for points located inside (resp. outside) the contour is constructed. The final lumen boundary surface is then represented by the zero level set of the interpolation of all these characteristic functions (Raya and Udupa Reference Raya and Udupa1990). Finally, we briefly describe interpolation by means of radial basis functions (RBFs), which provide a flexible way of interpolating data in multi-dimensional spaces, even for unstructured data where interpolation nodes are scattered and/or do not form a regular grid, and for which it is often impossible to apply polynomial or spline interpolation (Carr, Fright and Beatson Reference Carr, Fright and Beatson1997, Fornefett, Rohr and Stiehl Reference Fornefett, Rohr and Stiehl2001). The coefficients in the linear combination with respect to the RBF basis are determined by solving a suitable linear system, which is invertible under very mild conditions (Peiró et al.
Reference Peiró, Formaggia, Gazzola, Radaelli and Rigamonti2007).
A special mention must go to centreline reconstruction. The centreline is a one-dimensional curve centred inside the vessel lumen. Many segmentation tools use the centreline as the starting point, making the assumption that the shape of the section around each centreline location is known (O’Donnell, Jolly and Gupta Reference O’Donnell, Jolly and Gupta1998). Centreline reconstruction allows complete reconstruction of the computational domain when using one-dimensional modelling of blood flow: see Section 4.5.1.
In any case, at the end of the segmentation step we obtain the lattice
![]() ${\mathcal{L}}^{\mathit{surf}}$
which collects the points
${\mathcal{L}}^{\mathit{surf}}$
which collects the points
![]() $\boldsymbol{x}_{j}$
,
$\boldsymbol{x}_{j}$
,
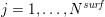 $j=1,\ldots ,N^{\mathit{surf}}$
, classified as belonging to the lumen vessel surface or to the outer wall, where
$j=1,\ldots ,N^{\mathit{surf}}$
, classified as belonging to the lumen vessel surface or to the outer wall, where
![]() $N^{\mathit{surf}}$
denotes the total number of points of the surface lattice.
$N^{\mathit{surf}}$
denotes the total number of points of the surface lattice.
3.1.4 Building the computational mesh
Once the final boundary lattice
![]() ${\mathcal{L}}^{\mathit{surf}}$
(made up of points on the lumen boundary) is made available, we are ready to build the volumetric mesh
${\mathcal{L}}^{\mathit{surf}}$
(made up of points on the lumen boundary) is made available, we are ready to build the volumetric mesh
![]() ${\mathcal{T}}^{\mathit{vol}}$
in the lumen. This mesh usually consists of unstructured tetrahedra, because of their flexibility in filling volumes of complex shape.
${\mathcal{T}}^{\mathit{vol}}$
in the lumen. This mesh usually consists of unstructured tetrahedra, because of their flexibility in filling volumes of complex shape.
Unstructured volumetric meshes are constructed starting from an analytical expression, say
![]() ${\mathcal{S}}(\boldsymbol{x})$
, representing the surface associated with the boundary lattice
${\mathcal{S}}(\boldsymbol{x})$
, representing the surface associated with the boundary lattice
![]() ${\mathcal{L}}^{\mathit{surf}}$
. This expression can derive from an explicit representation, for instance a bivariate parametric function built as a collection of adjacent polygons. The latter are typically triangles, generated by Lagrangian shape functions, or patches, generated by high-degree polynomials such as NURBS (Sun et al.
Reference Sun, Starly, Nam and Darling2005). Alternatively, the surface is represented implicitly as the isosurface of an embedding function. Note that some of the segmentation strategies described above, such as deformable models and those used for the surface reconstruction, directly provide an analytical expression
${\mathcal{L}}^{\mathit{surf}}$
. This expression can derive from an explicit representation, for instance a bivariate parametric function built as a collection of adjacent polygons. The latter are typically triangles, generated by Lagrangian shape functions, or patches, generated by high-degree polynomials such as NURBS (Sun et al.
Reference Sun, Starly, Nam and Darling2005). Alternatively, the surface is represented implicitly as the isosurface of an embedding function. Note that some of the segmentation strategies described above, such as deformable models and those used for the surface reconstruction, directly provide an analytical expression
![]() ${\mathcal{S}}(\boldsymbol{x})$
of the lumen boundary surface.
${\mathcal{S}}(\boldsymbol{x})$
of the lumen boundary surface.
For the construction of unstructured volumetric meshes
![]() ${\mathcal{T}}^{\mathit{vol}}$
, we mention two possible approaches. In the first, a boundary surface mesh
${\mathcal{T}}^{\mathit{vol}}$
, we mention two possible approaches. In the first, a boundary surface mesh
![]() ${\mathcal{T}}^{\mathit{surf}}$
is generated. To this end, we start from a lattice
${\mathcal{T}}^{\mathit{surf}}$
is generated. To this end, we start from a lattice
![]() $\widetilde{{\mathcal{L}}}^{\mathit{surf}}$
(in principle different to
$\widetilde{{\mathcal{L}}}^{\mathit{surf}}$
(in principle different to
![]() ${\mathcal{L}}^{\mathit{surf}}$
) composed of points of
${\mathcal{L}}^{\mathit{surf}}$
) composed of points of
![]() ${\mathcal{S}}$
. Then, the Voronoi diagram for
${\mathcal{S}}$
. Then, the Voronoi diagram for
![]() $\widetilde{{\mathcal{L}}}^{\mathit{surf}}$
is constructed. This is a partition of
$\widetilde{{\mathcal{L}}}^{\mathit{surf}}$
is constructed. This is a partition of
![]() ${\mathcal{S}}$
into non-overlapping regions, each one containing exactly one point (node) of
${\mathcal{S}}$
into non-overlapping regions, each one containing exactly one point (node) of
![]() $\widetilde{{\mathcal{L}}}^{\mathit{surf}}$
and composed of all the points of
$\widetilde{{\mathcal{L}}}^{\mathit{surf}}$
and composed of all the points of
![]() ${\mathcal{S}}$
that are closer to that node than to any other node. Starting from the Voronoi diagram, it is possible to generate a Delaunay mesh
${\mathcal{S}}$
that are closer to that node than to any other node. Starting from the Voronoi diagram, it is possible to generate a Delaunay mesh
![]() ${\mathcal{T}}^{\mathit{surf}}$
: see Thompson, Soni and Weatherill (Reference Thompson, Soni and Weatherill1999). We emphasize that the vertices of the mesh
${\mathcal{T}}^{\mathit{surf}}$
: see Thompson, Soni and Weatherill (Reference Thompson, Soni and Weatherill1999). We emphasize that the vertices of the mesh
![]() ${\mathcal{T}}^{\mathit{surf}}$
do not necessarily coincide with the points of the lattice
${\mathcal{T}}^{\mathit{surf}}$
do not necessarily coincide with the points of the lattice
![]() $\widetilde{{\mathcal{L}}}^{\mathit{surf}}$
. Popular algorithms for generating a Delaunay mesh have been proposed by Watson (Reference Watson1981) and Weatherill and Hassan (Reference Weatherill and Hassan1994). Once a surface mesh
$\widetilde{{\mathcal{L}}}^{\mathit{surf}}$
. Popular algorithms for generating a Delaunay mesh have been proposed by Watson (Reference Watson1981) and Weatherill and Hassan (Reference Weatherill and Hassan1994). Once a surface mesh
![]() ${\mathcal{T}}^{\mathit{surf}}$
is made available, the volumetric mesh
${\mathcal{T}}^{\mathit{surf}}$
is made available, the volumetric mesh
![]() ${\mathcal{T}}^{\mathit{vol}}$
is generated. The latter could be obtained by advancing front methods, where, starting from the triangles of the surface mesh, a front composed of internal nodes is generated. These new nodes allow us to identify tetrahedra, whose validity is verified by checking that they do not intersect the front (Bentley and Friedman Reference Bentley and Friedman1979).
${\mathcal{T}}^{\mathit{vol}}$
is generated. The latter could be obtained by advancing front methods, where, starting from the triangles of the surface mesh, a front composed of internal nodes is generated. These new nodes allow us to identify tetrahedra, whose validity is verified by checking that they do not intersect the front (Bentley and Friedman Reference Bentley and Friedman1979).
The second approach relies on directly generating the volumetric mesh
![]() ${\mathcal{T}}^{\mathit{vol}}$
, for example by means of Delaunay 3D mesh generation, where a starting volumetric lattice
${\mathcal{T}}^{\mathit{vol}}$
, for example by means of Delaunay 3D mesh generation, where a starting volumetric lattice
![]() $\widetilde{{\mathcal{L}}}^{\mathit{vol}}$
is obtained by locating the nodes in the volume
$\widetilde{{\mathcal{L}}}^{\mathit{vol}}$
is obtained by locating the nodes in the volume
![]() ${\mathcal{V}}(\boldsymbol{x})$
contained in
${\mathcal{V}}(\boldsymbol{x})$
contained in
![]() ${\mathcal{S}}(\boldsymbol{x})$
. One of the main problems related to this approach is that boundary meshing is often difficult, since the related surface triangulation could not be of Delaunay type. An alternative approach is given by octree mesh generation, where
${\mathcal{S}}(\boldsymbol{x})$
. One of the main problems related to this approach is that boundary meshing is often difficult, since the related surface triangulation could not be of Delaunay type. An alternative approach is given by octree mesh generation, where
![]() ${\mathcal{V}}(\boldsymbol{x})$
is embedded in a box and successive subdivisions are performed until the smallest cells permit accurate description of the boundary. Despite being faster, this strategy generates meshes with poor quality near the boundary.
${\mathcal{V}}(\boldsymbol{x})$
is embedded in a box and successive subdivisions are performed until the smallest cells permit accurate description of the boundary. Despite being faster, this strategy generates meshes with poor quality near the boundary.
When a volumetric mesh
![]() ${\mathcal{T}}^{\mathit{vol}}$
is obtained, a further step (mesh optimization) could be introduced prior to the generation of the final mesh, so as to improve its quality. This prevents mesh distortion, for example the presence of very small angles, which could reduce the convergence of algorithms for the solution of the PDE of interest and thus their accuracy. Mesh optimization is incorporated in the strategies described above; it leads to an optimal mesh, providing the best accuracy for a given number of nodes.
${\mathcal{T}}^{\mathit{vol}}$
is obtained, a further step (mesh optimization) could be introduced prior to the generation of the final mesh, so as to improve its quality. This prevents mesh distortion, for example the presence of very small angles, which could reduce the convergence of algorithms for the solution of the PDE of interest and thus their accuracy. Mesh optimization is incorporated in the strategies described above; it leads to an optimal mesh, providing the best accuracy for a given number of nodes.
A mesh is deemed valid for blood flow simulations if it allows recovery of outputs of physical interest. In arteries, the mesh should be fine enough to capture wall shear stress (WSS) (Celik et al.
Reference Celik, Ghia, Roache, Freitas, Coleman and Raad2008) and, to this end, the construction of a boundary layer mesh is essential, even at low Reynolds numbers (Bevan et al.
Reference Bevan, Nithiarasu, van Loon, Sazonov, Luckraz and Garnham2010). Here
![]() $\mathit{WSS}$
expresses the magnitude of tangential viscous forces exerted by the fluid on the lumen boundary
$\mathit{WSS}$
expresses the magnitude of tangential viscous forces exerted by the fluid on the lumen boundary
![]() $\unicode[STIX]{x1D6F4}^{t}$
, defined by
$\unicode[STIX]{x1D6F4}^{t}$
, defined by
 $$\begin{eqnarray}\mathit{WSS}=\unicode[STIX]{x1D707}\sqrt{\mathop{\sum }_{j=1}^{2}((\unicode[STIX]{x1D6FB}\boldsymbol{v}\,\boldsymbol{n})\cdot \boldsymbol{\unicode[STIX]{x1D70F}}^{(j)})^{2}}\quad \text{on }\unicode[STIX]{x1D6F4}^{t},\end{eqnarray}$$
$$\begin{eqnarray}\mathit{WSS}=\unicode[STIX]{x1D707}\sqrt{\mathop{\sum }_{j=1}^{2}((\unicode[STIX]{x1D6FB}\boldsymbol{v}\,\boldsymbol{n})\cdot \boldsymbol{\unicode[STIX]{x1D70F}}^{(j)})^{2}}\quad \text{on }\unicode[STIX]{x1D6F4}^{t},\end{eqnarray}$$
where
![]() $\boldsymbol{v}$
is the fluid velocity,
$\boldsymbol{v}$
is the fluid velocity,
![]() $\boldsymbol{n}$
is the outward unit vector, and
$\boldsymbol{n}$
is the outward unit vector, and
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}^{(j)}$
,
$\boldsymbol{\unicode[STIX]{x1D70F}}^{(j)}$
,
![]() $j=1,2$
, represent the tangential unit vectors. Note that
$j=1,2$
, represent the tangential unit vectors. Note that
![]() $\mathit{WSS}$
is a scalar function of
$\mathit{WSS}$
is a scalar function of
![]() $\boldsymbol{x}\in \unicode[STIX]{x1D6F4}^{t}$
and
$\boldsymbol{x}\in \unicode[STIX]{x1D6F4}^{t}$
and
![]() $t>0$
. In componentwise notation,
$t>0$
. In componentwise notation,
 $$\begin{eqnarray}\mathit{WSS}=\unicode[STIX]{x1D707}\left(\mathop{\sum }_{j=1}^{2}\left(\mathop{\sum }_{i,k=1}^{3}\biggl(\frac{\unicode[STIX]{x2202}v_{i}}{\unicode[STIX]{x2202}x_{k}}n_{k}\biggr)\unicode[STIX]{x1D70F}_{i}^{(j)}\right)^{2}\right)^{1/2}\quad \text{on }\unicode[STIX]{x1D6F4}^{t}.\end{eqnarray}$$
$$\begin{eqnarray}\mathit{WSS}=\unicode[STIX]{x1D707}\left(\mathop{\sum }_{j=1}^{2}\left(\mathop{\sum }_{i,k=1}^{3}\biggl(\frac{\unicode[STIX]{x2202}v_{i}}{\unicode[STIX]{x2202}x_{k}}n_{k}\biggr)\unicode[STIX]{x1D70F}_{i}^{(j)}\right)^{2}\right)^{1/2}\quad \text{on }\unicode[STIX]{x1D6F4}^{t}.\end{eqnarray}$$
For the structure domain, hexahedral meshing is preferable so as to prevent the locking phenomenon, whereas tetrahedral meshes are used when conforming meshes at the boundary lumen interface are needed, in view of fluid–structure interaction problems (see Section 4.3). Usually, three or four layers of elements are enough to obtain an accurate result (Younis et al. Reference Younis, Kaazempur-Mofrad, Chan, Isasi, Hinton, Chau, Kim and Kamm2004).
For recent reviews on geometric reconstruction for blood flow simulation, see Antiga et al. (Reference Antiga, Peiró, Steinman, Formaggia, Quarteroni and Veneziani2009), Sazonov et al. (Reference Sazonov, Yeo, Bevan, Xie, van Loon and Nithiarasu2011) and Lesage et al. (Reference Lesage, Angelini, Bloch and Funka-Lea2009).
3.2 Boundary vascular data
The differential equations we will treat in the following sections need appropriate boundary conditions. For our problems (incompressible Navier–Stokes equations for the fluid and finite elasticity for the structure), we anticipate the kind of boundary conditions that should ideally be prescribed, namely
 $$\begin{eqnarray}\boldsymbol{v}=\boldsymbol{g}_{f}\quad \text{on }\unicode[STIX]{x1D6E4}_{f}^{D,t},\quad -p\boldsymbol{n}+\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FB}\boldsymbol{v}+(\unicode[STIX]{x1D6FB}\boldsymbol{v})^{T})\boldsymbol{n}=\boldsymbol{h}_{f}\quad \text{on }\unicode[STIX]{x1D6E4}_{f}^{N,t}\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{v}=\boldsymbol{g}_{f}\quad \text{on }\unicode[STIX]{x1D6E4}_{f}^{D,t},\quad -p\boldsymbol{n}+\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FB}\boldsymbol{v}+(\unicode[STIX]{x1D6FB}\boldsymbol{v})^{T})\boldsymbol{n}=\boldsymbol{h}_{f}\quad \text{on }\unicode[STIX]{x1D6E4}_{f}^{N,t}\end{eqnarray}$$
for the fluid problem and
 $$\begin{eqnarray}\boldsymbol{d}=\boldsymbol{g}_{s}\quad \text{on }\unicode[STIX]{x1D6E4}_{s}^{D,t},\quad \boldsymbol{T}_{s}\boldsymbol{n}=\boldsymbol{h}_{s}\quad \text{on }\unicode[STIX]{x1D6E4}_{s}^{N,t}\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{d}=\boldsymbol{g}_{s}\quad \text{on }\unicode[STIX]{x1D6E4}_{s}^{D,t},\quad \boldsymbol{T}_{s}\boldsymbol{n}=\boldsymbol{h}_{s}\quad \text{on }\unicode[STIX]{x1D6E4}_{s}^{N,t}\end{eqnarray}$$
for the structure problem. In the above equations, the Dirichlet and Neumann boundaries,
![]() $\unicode[STIX]{x1D6E4}_{j}^{D,t}$
and
$\unicode[STIX]{x1D6E4}_{j}^{D,t}$
and
![]() $\unicode[STIX]{x1D6E4}_{j}^{N,t}$
, respectively, are such that
$\unicode[STIX]{x1D6E4}_{j}^{N,t}$
, respectively, are such that
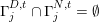 $\unicode[STIX]{x1D6E4}_{j}^{D,t}\cap \unicode[STIX]{x1D6E4}_{j}^{N,t}=\emptyset$
,
$\unicode[STIX]{x1D6E4}_{j}^{D,t}\cap \unicode[STIX]{x1D6E4}_{j}^{N,t}=\emptyset$
,
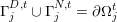 $\unicode[STIX]{x1D6E4}_{j}^{D,t}\cup \unicode[STIX]{x1D6E4}_{j}^{N,t}=\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}_{j}^{t}$
,
$\unicode[STIX]{x1D6E4}_{j}^{D,t}\cup \unicode[STIX]{x1D6E4}_{j}^{N,t}=\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}_{j}^{t}$
,
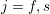 $j=f,s$
, where
$j=f,s$
, where
![]() $\unicode[STIX]{x1D6FA}_{f}^{t}$
and
$\unicode[STIX]{x1D6FA}_{f}^{t}$
and
![]() $\unicode[STIX]{x1D6FA}_{s}^{t}$
are the fluid and structure domains at time
$\unicode[STIX]{x1D6FA}_{s}^{t}$
are the fluid and structure domains at time
![]() $t$
: see Figure 3.1(a). Moreover,
$t$
: see Figure 3.1(a). Moreover,
![]() $p$
denotes the fluid pressure,
$p$
denotes the fluid pressure,
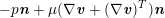 $-p\boldsymbol{n}+\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FB}\boldsymbol{v}+(\unicode[STIX]{x1D6FB}\boldsymbol{v})^{T})\boldsymbol{n}$
is the fluid normal Cauchy stress,
$-p\boldsymbol{n}+\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FB}\boldsymbol{v}+(\unicode[STIX]{x1D6FB}\boldsymbol{v})^{T})\boldsymbol{n}$
is the fluid normal Cauchy stress,
![]() $\boldsymbol{d}$
is the structure displacement,
$\boldsymbol{d}$
is the structure displacement,
![]() $\boldsymbol{T}_{s}$
is the Cauchy stress tensor of the wall material, and
$\boldsymbol{T}_{s}$
is the Cauchy stress tensor of the wall material, and
![]() $\boldsymbol{g}_{f}$
,
$\boldsymbol{g}_{f}$
,
![]() $\boldsymbol{g}_{s}$
,
$\boldsymbol{g}_{s}$
,
![]() $\boldsymbol{h}_{f}$
,
$\boldsymbol{h}_{f}$
,
![]() $\boldsymbol{h}_{s}$
are data: see Section 4. We use the superscript
$\boldsymbol{h}_{s}$
are data: see Section 4. We use the superscript
![]() $^{t}$
to indicate time-dependence.
$^{t}$
to indicate time-dependence.
As we will see below, the boundary of the computational domain (for either the fluid or the structure) will be composed of two parts, namely the physical boundary and the artificial boundary. On the physical boundary, suitable conditions are often suggested by physical principles. For example, for the fluid problem, no-slip Dirichlet conditions should be prescribed at the lumen boundary, since it is assumed that the fluid particles perfectly adhere to the vessel wall. This leads to a homogeneous Dirichlet condition (
![]() $\boldsymbol{v}=\mathbf{0}$
) in the case of rigid walls, and to a kinematic interface condition (
$\boldsymbol{v}=\mathbf{0}$
) in the case of rigid walls, and to a kinematic interface condition (
![]() $\boldsymbol{v}=\dot{\boldsymbol{d}}$
) for fluid–structure interaction problems (see Section 4.3). As for the structure problem, at the internal physical boundary (i.e. at the lumen boundary) the fluid pressure is often prescribed. This leads to a Neumann boundary condition (
$\boldsymbol{v}=\dot{\boldsymbol{d}}$
) for fluid–structure interaction problems (see Section 4.3). As for the structure problem, at the internal physical boundary (i.e. at the lumen boundary) the fluid pressure is often prescribed. This leads to a Neumann boundary condition (
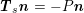 $\boldsymbol{T}_{s}\boldsymbol{n}=-P\boldsymbol{n}$
, where
$\boldsymbol{T}_{s}\boldsymbol{n}=-P\boldsymbol{n}$
, where
![]() $P$
is a measurement of the fluid pressure) for a pure structure problem, and to a dynamic interface condition (
$P$
is a measurement of the fluid pressure) for a pure structure problem, and to a dynamic interface condition (
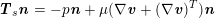 $\boldsymbol{T}_{s}\boldsymbol{n}=-p\boldsymbol{n}+\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FB}\boldsymbol{v}+(\unicode[STIX]{x1D6FB}\boldsymbol{v})^{T})\boldsymbol{n}$
) for fluid–structure interaction. On the outer wall boundary
$\boldsymbol{T}_{s}\boldsymbol{n}=-p\boldsymbol{n}+\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FB}\boldsymbol{v}+(\unicode[STIX]{x1D6FB}\boldsymbol{v})^{T})\boldsymbol{n}$
) for fluid–structure interaction. On the outer wall boundary
![]() $\unicode[STIX]{x1D6E4}_{\mathit{ext}}$
, the interaction with the surrounding tissue should be considered. This is often modelled by means of a Robin boundary condition of the form
$\unicode[STIX]{x1D6E4}_{\mathit{ext}}$
, the interaction with the surrounding tissue should be considered. This is often modelled by means of a Robin boundary condition of the form
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{ST}\boldsymbol{d}+\boldsymbol{T}_{s}\boldsymbol{n}=P_{\mathit{ext}}\boldsymbol{n}\quad \text{on }\unicode[STIX]{x1D6E4}_{\mathit{ext}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{ST}\boldsymbol{d}+\boldsymbol{T}_{s}\boldsymbol{n}=P_{\mathit{ext}}\boldsymbol{n}\quad \text{on }\unicode[STIX]{x1D6E4}_{\mathit{ext}},\end{eqnarray}$$
which assimilates the surrounding tissue to a sequence of elastic springs with rigidity
![]() $\unicode[STIX]{x1D6FC}_{ST}$
and where
$\unicode[STIX]{x1D6FC}_{ST}$
and where
![]() $P_{\mathit{ext}}$
is the external pressure (Moireau et al.
Reference Moireau, Xiao, Astorino, Figueroa, Chapelle, Taylor and Gerbeau2012).
$P_{\mathit{ext}}$
is the external pressure (Moireau et al.
Reference Moireau, Xiao, Astorino, Figueroa, Chapelle, Taylor and Gerbeau2012).
In contrast, the artificial sections are those introduced by the truncation of the computational domains: see Figure 3.1(b). Truncation is done in order to focus on a specific domain of interest. Ideally, the boundary conditions to be used on artificial sections should derive from clinical measurements.

Figure 3.1. Possible choices of the Dirichlet and Neumann boundaries (a) and physical and artificial boundaries (b) for a carotid domain in the fluid stand-alone problem (reconstructed from MRA images).
The technique mainly used to obtain boundary data on artificial boundaries is ultrasound. This is because of its non-invasiveness and the fact that it is used daily in clinical practice. If the ultrasound beam is swept through a plane or sector (unlike in geometric acquisitions where it is kept fixed), it is possible to measure the blood velocity at a single point of a cross-section
![]() $\unicode[STIX]{x1D6E4}^{t}$
in the direction of the ultrasound beam by exploiting the Doppler effect. The velocity is then converted into a flow rate measure
$\unicode[STIX]{x1D6E4}^{t}$
in the direction of the ultrasound beam by exploiting the Doppler effect. The velocity is then converted into a flow rate measure
![]() $Q$
across
$Q$
across
![]() $\unicode[STIX]{x1D6E4}^{t}$
for each time (this is the principle of the so-called echo-colour-Doppler technique: Savader, Lund and Osterman Reference Savader, Lund and Osterman1997) and can then be used to prescribe a flow rate condition
$\unicode[STIX]{x1D6E4}^{t}$
for each time (this is the principle of the so-called echo-colour-Doppler technique: Savader, Lund and Osterman Reference Savader, Lund and Osterman1997) and can then be used to prescribe a flow rate condition
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{f}\int _{\unicode[STIX]{x1D6E4}^{t}}\boldsymbol{v}\cdot \boldsymbol{n}\text{d}\unicode[STIX]{x1D6FE}=Q.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{f}\int _{\unicode[STIX]{x1D6E4}^{t}}\boldsymbol{v}\cdot \boldsymbol{n}\text{d}\unicode[STIX]{x1D6FE}=Q.\end{eqnarray}$$
Condition (3.2) is defective since it is not enough to ensure well-posedness of the fluid problem. The treatment of defective conditions will be addressed in Section 4.4. Another technique allowing measurement of cross-sectional flow rates is based on the acquisition of thermal images (Mahmoud et al.
Reference Mahmoud, El-Barkouky, Farag, Graham and Farag2013). Another quantity easily measurable by means of ultrasound is the lumen area
![]() $\int _{\unicode[STIX]{x1D6E4}^{t}}\text{d}\unicode[STIX]{x1D6FE}$
. This information could be used to prescribe a defective condition for the vessel wall.
$\int _{\unicode[STIX]{x1D6E4}^{t}}\text{d}\unicode[STIX]{x1D6FE}$
. This information could be used to prescribe a defective condition for the vessel wall.
More sophisticated techniques could acquire velocity measurements in several points on the same cross-section, thus in principle leading to a Dirichlet boundary condition (possibly after suitable regularization). This is the case for phase contrast (PC)-MRA, where the blood velocities are encoded into images taken at several instants during a heartbeat (Morbiducci et al.
Reference Morbiducci, Ponzini, Rizzo, Cadioli, Esposito, De Cobelli, Del Maschio, Montevecchi and Redaelli2009). The spatial resolution of modern PC-MRA is of the order of
![]() $1$
–
$1$
–
![]() $2~\text{mm}$
on each cross-section and
$2~\text{mm}$
on each cross-section and
![]() $4~\text{mm}$
along the longitudinal axis. The required mesh size is often less than
$4~\text{mm}$
along the longitudinal axis. The required mesh size is often less than
![]() $1~\text{mm}$
, however, so interpolation is needed to obtain a usable Dirichlet condition. The temporal resolution is about
$1~\text{mm}$
, however, so interpolation is needed to obtain a usable Dirichlet condition. The temporal resolution is about
![]() $0.03~\text{s}$
.
$0.03~\text{s}$
.
If the lumen artificial cross-section is orthogonal to the axial direction, then the viscous terms in the fluid normal Cauchy stress are very small (Heywood, Rannacher and Turek Reference Heywood, Rannacher and Turek1996). In this case, a measurement of the pressure
![]() $P(t)$
could be used to prescribe a Neumann boundary condition. This could be obtained for the arterial system non-invasively by means of a sphygmomanometer, which usually measures the pressure at the level of the radial aorta (remember that the pressure peak could be considered constant along the arterial tree, at least until the capillary net: see Section 2). To have continuous monitoring of the pressure (e.g. during hospital recovery) or to take a measurement in the venous system (where the pressure reduces), a catheter with a transducer could be placed in the district of interest. In any case, the average pressure over the cross-section is measured. This leads at each time to the following defective boundary condition for the normal component of the normal Cauchy stress of the fluid:
$P(t)$
could be used to prescribe a Neumann boundary condition. This could be obtained for the arterial system non-invasively by means of a sphygmomanometer, which usually measures the pressure at the level of the radial aorta (remember that the pressure peak could be considered constant along the arterial tree, at least until the capillary net: see Section 2). To have continuous monitoring of the pressure (e.g. during hospital recovery) or to take a measurement in the venous system (where the pressure reduces), a catheter with a transducer could be placed in the district of interest. In any case, the average pressure over the cross-section is measured. This leads at each time to the following defective boundary condition for the normal component of the normal Cauchy stress of the fluid:
 $$\begin{eqnarray}\frac{1}{|\unicode[STIX]{x1D6E4}^{t}|}\int _{\unicode[STIX]{x1D6E4}^{t}}(p\boldsymbol{n}-\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FB}\boldsymbol{v}+(\unicode[STIX]{x1D6FB}\boldsymbol{v})^{T})\boldsymbol{n})\cdot \boldsymbol{n}\text{d}\unicode[STIX]{x1D6FE}=P.\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{|\unicode[STIX]{x1D6E4}^{t}|}\int _{\unicode[STIX]{x1D6E4}^{t}}(p\boldsymbol{n}-\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FB}\boldsymbol{v}+(\unicode[STIX]{x1D6FB}\boldsymbol{v})^{T})\boldsymbol{n})\cdot \boldsymbol{n}\text{d}\unicode[STIX]{x1D6FE}=P.\end{eqnarray}$$
Unfortunately, no measurement is available at the artificial sections of the structure, so ‘empirical’ and ‘practical’ choices are made (see Section 4.4).
Finally, we observe that measurements acquired at several instants during a heartbeat could be used in principle for physical boundaries as well. For example, from 4D-CTA the boundary lumen displacement could be used as the Dirichlet condition for the structure problem, whereas from PC-MRA the blood velocity at the boundary lumen could be used to prescribe a Dirichlet condition for the fluid problem. Since, at the physical boundaries, physical principles are used to prescribe boundary conditions, these ‘extra’ data could be used for validation of the numerical results or in a parameter estimation fashion, as described in Section 10. PC-MRA also allows us to acquire internal measurements of blood velocity. This could also be used for validation or parameter estimation.
3.3 Biological vascular data
Finally, we need to know the values of physical parameters appearing in the differential equations. For the fluid, two parameters characterize the problem, namely blood density and blood viscosity. Although density is easily measurable in principle, no patient-specific acquisition is made in general because its value never significantly departs from an average value of
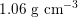 $1.06~\text{g}~\text{cm}^{-3}$
. In contrast, the range of variability of viscosity is larger. Indeed, its value depends on the shear rate (non-Newtonian behaviour) and on the physical state of the patient. When the assumption of Newtonian fluid (holding for medium and large healthy vessels) is made, typical values of the viscosity range in the interval 0.03–0.04 P (= 1 g
$1.06~\text{g}~\text{cm}^{-3}$
. In contrast, the range of variability of viscosity is larger. Indeed, its value depends on the shear rate (non-Newtonian behaviour) and on the physical state of the patient. When the assumption of Newtonian fluid (holding for medium and large healthy vessels) is made, typical values of the viscosity range in the interval 0.03–0.04 P (= 1 g
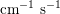 $\text{cm}^{-1}~\text{s}^{-1}$
). Again, no patient-specific viscosity measurements are usually made and, except for pathological situations, a value in the previous range is selected.
$\text{cm}^{-1}~\text{s}^{-1}$
). Again, no patient-specific viscosity measurements are usually made and, except for pathological situations, a value in the previous range is selected.
The parameters characterizing the vessel wall depend (also in number) on the constitutive law used to represent its behaviour. More typically, they are the density, the elasticity (or compliance) and the degree of incompressibility. For linear elasticity models, the latter two are quantified by Young’s modulus and the Poisson modulus, respectively. The density value is very similar to that of blood, the range most commonly used reaching values up to 1.2
![]() $\text{g}~\text{cm}^{-3}$
. The compliance of the vessel could be qualitatively seen as the ratio between the volume and pressure variations (Nichols and O’Rourke Reference Nichols and O’Rourke2005). Patient-specific measurements could be obtained from simultaneous (invasive) measurement of pressure and cross-sectional area at different locations, by measuring the rate of propagation of flow waves (Boese et al.
Reference Boese, Bock, Schoenberg and Schad2000), or by elastography, where the elasticity properties are analysed by images before and after a deformation (Oberai, Gokhale and Feijóo Reference Oberai, Gokhale and Feijóo2003). The range of variability of vessel compliance is quite wide (200–800 kPa in normal conditions), with great dependence on the location and on the possible presence of aneurysms or calcifications. As for the Poisson modulus, only ex vivo measurements are possible. An acceptable value used by the community is
$\text{g}~\text{cm}^{-3}$
. The compliance of the vessel could be qualitatively seen as the ratio between the volume and pressure variations (Nichols and O’Rourke Reference Nichols and O’Rourke2005). Patient-specific measurements could be obtained from simultaneous (invasive) measurement of pressure and cross-sectional area at different locations, by measuring the rate of propagation of flow waves (Boese et al.
Reference Boese, Bock, Schoenberg and Schad2000), or by elastography, where the elasticity properties are analysed by images before and after a deformation (Oberai, Gokhale and Feijóo Reference Oberai, Gokhale and Feijóo2003). The range of variability of vessel compliance is quite wide (200–800 kPa in normal conditions), with great dependence on the location and on the possible presence of aneurysms or calcifications. As for the Poisson modulus, only ex vivo measurements are possible. An acceptable value used by the community is
![]() $0.49$
, meaning that vessels could be considered as quasi-incompressible. Finally, let us mention that the coefficient
$0.49$
, meaning that vessels could be considered as quasi-incompressible. Finally, let us mention that the coefficient
![]() $\unicode[STIX]{x1D6FC}_{ST}$
in (3.1) can be regarded as representative of the Young’s modulus of the surrounding tissue. As such, it could thus be measured, though this is a difficult endeavour. Estimates have been provided in Liu et al. (Reference Liu, Charles, Gracia, Gregersen and Kassab2007), for example.
$\unicode[STIX]{x1D6FC}_{ST}$
in (3.1) can be regarded as representative of the Young’s modulus of the surrounding tissue. As such, it could thus be measured, though this is a difficult endeavour. Estimates have been provided in Liu et al. (Reference Liu, Charles, Gracia, Gregersen and Kassab2007), for example.
When not available from measurements, patient-specific values of biological data could alternatively be obtained by means of parameter estimation mathematical techniques. This will be the topic of Section 10.
4 Modelling blood flow
4.1 The fluid problem
In large and medium sized arteries – those more typically affected by vascular diseases – blood can be modelled by means of the Navier–Stokes (NS) equations for incompressible homogeneous Newtonian fluids (Perktold, Thurner and Kenner Reference Perktold, Thurner and Kenner1994, Taylor, Hughes and Zarins Reference Taylor, Hughes and Zarins1996, Reference Taylor, Hughes and Zarins1998, Formaggia et al. Reference Formaggia, Quarteroni and Veneziani2009a ). For non-Newtonian rheological models necessary to describe some specific flow processes, such as clotting or sickle cell diseases, or more generally flow in capillaries, we refer to Robertson, Sequeira and Owens (Reference Robertson, Sequeira, Owens, Formaggia, Quarteroni and Veneziani2009) and Fasano, Santos and Sequeira (Reference Fasano, Santos, Sequeira, Ambrosi, Quarteroni and Rozza2012), for example.
For the mathematical formulation of the problem, we write the fluid equations with respect to an Eulerian frame of reference, and we let
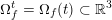 $\unicode[STIX]{x1D6FA}_{f}^{t}=\unicode[STIX]{x1D6FA}_{f}(t)\subset \mathbb{R}^{3}$
denote the time-varying arterial lumen, at time
$\unicode[STIX]{x1D6FA}_{f}^{t}=\unicode[STIX]{x1D6FA}_{f}(t)\subset \mathbb{R}^{3}$
denote the time-varying arterial lumen, at time
![]() $t>0$
(see Figure 4.1(a)).
$t>0$
(see Figure 4.1(a)).

Figure 4.1. Representation of the fluid domain (a) and structure domain (b). The fluid domain illustrated is that of an abdominal aorta in the presence of an aneurysm, reconstructed from CTA images. The structure domain was obtained via extrusion of the fluid domain.
Then, at each time
![]() $t>0$
, we look for fluid velocity
$t>0$
, we look for fluid velocity
![]() $\boldsymbol{v}$
and fluid pressure
$\boldsymbol{v}$
and fluid pressure
![]() $p$
such that
$p$
such that
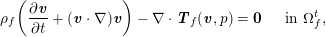 $$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D70C}_{f}\biggl(\displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{v}}{\unicode[STIX]{x2202}t}+(\boldsymbol{v}\cdot \unicode[STIX]{x1D6FB})\boldsymbol{v}\biggr)-\unicode[STIX]{x1D6FB}\cdot \boldsymbol{T}_{f}(\boldsymbol{v},p)=\mathbf{0} & & \displaystyle \displaystyle \quad \text{in }\unicode[STIX]{x1D6FA}_{f}^{t},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D70C}_{f}\biggl(\displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{v}}{\unicode[STIX]{x2202}t}+(\boldsymbol{v}\cdot \unicode[STIX]{x1D6FB})\boldsymbol{v}\biggr)-\unicode[STIX]{x1D6FB}\cdot \boldsymbol{T}_{f}(\boldsymbol{v},p)=\mathbf{0} & & \displaystyle \displaystyle \quad \text{in }\unicode[STIX]{x1D6FA}_{f}^{t},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D6FB}\cdot \boldsymbol{v}=0 & & \displaystyle \displaystyle \quad \text{in }\unicode[STIX]{x1D6FA}_{f}^{t}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D6FB}\cdot \boldsymbol{v}=0 & & \displaystyle \displaystyle \quad \text{in }\unicode[STIX]{x1D6FA}_{f}^{t}.\end{eqnarray}$$
 $$\begin{eqnarray}\boldsymbol{T}_{f}(\boldsymbol{v},p)=-p\boldsymbol{I}+\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FB}\boldsymbol{v}+(\unicode[STIX]{x1D6FB}\boldsymbol{v})^{T})\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{T}_{f}(\boldsymbol{v},p)=-p\boldsymbol{I}+\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FB}\boldsymbol{v}+(\unicode[STIX]{x1D6FB}\boldsymbol{v})^{T})\end{eqnarray}$$
is the fluid Cauchy stress tensor, where
![]() $\unicode[STIX]{x1D707}$
is the blood viscosity. As we consider only Newtonian rheology here,
$\unicode[STIX]{x1D707}$
is the blood viscosity. As we consider only Newtonian rheology here,
![]() $\unicode[STIX]{x1D707}$
is assumed to be constant.
$\unicode[STIX]{x1D707}$
is assumed to be constant.
Finally, problem (4.1) is completed by the initial condition
 $$\begin{eqnarray}\boldsymbol{v}|_{t=0}=\boldsymbol{v}_{0}\quad \text{in }\unicode[STIX]{x1D6FA}_{f},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{v}|_{t=0}=\boldsymbol{v}_{0}\quad \text{in }\unicode[STIX]{x1D6FA}_{f},\end{eqnarray}$$
where
 $\unicode[STIX]{x1D6FA}_{f}=\unicode[STIX]{x1D6FA}_{f}^{0}$
, and boundary conditions. The latter typically prescribe no-slip conditions on the physical boundary
$\unicode[STIX]{x1D6FA}_{f}=\unicode[STIX]{x1D6FA}_{f}^{0}$
, and boundary conditions. The latter typically prescribe no-slip conditions on the physical boundary
![]() $\unicode[STIX]{x1D6F4}^{t}$
,
$\unicode[STIX]{x1D6F4}^{t}$
,
 $$\begin{eqnarray}\boldsymbol{v}=\boldsymbol{\unicode[STIX]{x1D719}}\quad \text{on }\unicode[STIX]{x1D6F4}^{t},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{v}=\boldsymbol{\unicode[STIX]{x1D719}}\quad \text{on }\unicode[STIX]{x1D6F4}^{t},\end{eqnarray}$$
the upstream velocity on the proximal boundaries, say
![]() $\unicode[STIX]{x1D6E4}_{\mathit{in}}^{t}$
,
$\unicode[STIX]{x1D6E4}_{\mathit{in}}^{t}$
,
 $$\begin{eqnarray}\boldsymbol{v}=\boldsymbol{v}_{\mathit{up}}\quad \text{on }\unicode[STIX]{x1D6E4}_{\mathit{in}}^{t},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{v}=\boldsymbol{v}_{\mathit{up}}\quad \text{on }\unicode[STIX]{x1D6E4}_{\mathit{in}}^{t},\end{eqnarray}$$
and traction conditions on the distal boundaries, say
![]() $\unicode[STIX]{x1D6E4}_{\mathit{out}}^{t}$
,
$\unicode[STIX]{x1D6E4}_{\mathit{out}}^{t}$
,
 $$\begin{eqnarray}\boldsymbol{T}_{f}\,\boldsymbol{n}=\boldsymbol{h}_{f}\quad \text{on }\unicode[STIX]{x1D6E4}_{\mathit{out}}^{t}.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{T}_{f}\,\boldsymbol{n}=\boldsymbol{h}_{f}\quad \text{on }\unicode[STIX]{x1D6E4}_{\mathit{out}}^{t}.\end{eqnarray}$$
Here,
![]() $\boldsymbol{v}_{0}$
,
$\boldsymbol{v}_{0}$
,
![]() $\boldsymbol{v}_{\mathit{up}}$
,
$\boldsymbol{v}_{\mathit{up}}$
,
![]() $\boldsymbol{\unicode[STIX]{x1D719}}$
and
$\boldsymbol{\unicode[STIX]{x1D719}}$
and
![]() $\boldsymbol{h}_{f}$
are suitable functions with the required regularity (Quarteroni and Valli Reference Quarteroni and Valli1994). Note that the lumen boundary displacement
$\boldsymbol{h}_{f}$
are suitable functions with the required regularity (Quarteroni and Valli Reference Quarteroni and Valli1994). Note that the lumen boundary displacement
![]() $\boldsymbol{\unicode[STIX]{x1D719}}$
at this level is a known function of space and time. For rigid boundaries, we have
$\boldsymbol{\unicode[STIX]{x1D719}}$
at this level is a known function of space and time. For rigid boundaries, we have
![]() $\boldsymbol{\unicode[STIX]{x1D719}}=\mathbf{0}$
.
$\boldsymbol{\unicode[STIX]{x1D719}}=\mathbf{0}$
.
When patient-specific measurements are available, other conditions might be prescribed. However, measurements seldom provide a complete dataset to be used in the computation: see our discussion in Section 3.2. This prompts the issue of solvability of Navier–Stokes equations, which we address in Section 4.4.
For each
![]() $t>0$
(a.e.
$t>0$
(a.e.
![]() $t>0$
), the weak form of (4.1) together with the boundary conditions (4.3, 4.4, 4.5) reads as follows: find
$t>0$
), the weak form of (4.1) together with the boundary conditions (4.3, 4.4, 4.5) reads as follows: find
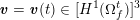 $\boldsymbol{v}=\boldsymbol{v}(t)\in [H^{1}(\unicode[STIX]{x1D6FA}_{f}^{t})]^{3}$
,
$\boldsymbol{v}=\boldsymbol{v}(t)\in [H^{1}(\unicode[STIX]{x1D6FA}_{f}^{t})]^{3}$
,
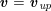 $\boldsymbol{v}=\boldsymbol{v}_{\mathit{up}}$
on
$\boldsymbol{v}=\boldsymbol{v}_{\mathit{up}}$
on
![]() $\unicode[STIX]{x1D6E4}_{\mathit{in}}^{t}$
,
$\unicode[STIX]{x1D6E4}_{\mathit{in}}^{t}$
,
![]() $\boldsymbol{v}=\boldsymbol{\unicode[STIX]{x1D719}}$
on
$\boldsymbol{v}=\boldsymbol{\unicode[STIX]{x1D719}}$
on
![]() $\unicode[STIX]{x1D6F4}^{t}$
,
$\unicode[STIX]{x1D6F4}^{t}$
,
![]() $\boldsymbol{v}=\boldsymbol{v}_{0}$
for
$\boldsymbol{v}=\boldsymbol{v}_{0}$
for
![]() $t=0$
in
$t=0$
in
![]() $\unicode[STIX]{x1D6FA}_{f}$
, and
$\unicode[STIX]{x1D6FA}_{f}$
, and
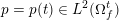 $p=p(t)\in L^{2}(\unicode[STIX]{x1D6FA}_{f}^{t})$
such that
$p=p(t)\in L^{2}(\unicode[STIX]{x1D6FA}_{f}^{t})$
such that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D70C}_{f}\int _{\unicode[STIX]{x1D6FA}_{f}^{t}}\frac{\unicode[STIX]{x2202}\boldsymbol{v}}{\unicode[STIX]{x2202}t}\cdot \boldsymbol{w}\text{d}\unicode[STIX]{x1D714}+{\mathcal{A}}_{f}^{t}(\boldsymbol{v},\boldsymbol{v},\boldsymbol{w})+{\mathcal{B}}^{t}(p,\boldsymbol{w})=\int _{\unicode[STIX]{x1D6E4}_{\mathit{out}}^{t}}\boldsymbol{h}_{f}\cdot \boldsymbol{n}\text{d}\unicode[STIX]{x1D6FE},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D70C}_{f}\int _{\unicode[STIX]{x1D6FA}_{f}^{t}}\frac{\unicode[STIX]{x2202}\boldsymbol{v}}{\unicode[STIX]{x2202}t}\cdot \boldsymbol{w}\text{d}\unicode[STIX]{x1D714}+{\mathcal{A}}_{f}^{t}(\boldsymbol{v},\boldsymbol{v},\boldsymbol{w})+{\mathcal{B}}^{t}(p,\boldsymbol{w})=\int _{\unicode[STIX]{x1D6E4}_{\mathit{out}}^{t}}\boldsymbol{h}_{f}\cdot \boldsymbol{n}\text{d}\unicode[STIX]{x1D6FE},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{B}}^{t}(q,\boldsymbol{v})=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{B}}^{t}(q,\boldsymbol{v})=0,\end{eqnarray}$$
 $$\begin{eqnarray}\boldsymbol{w}\in \boldsymbol{V}^{t}=\{[H^{1}(\unicode[STIX]{x1D6FA}_{f}^{t})]^{3}:\,\boldsymbol{w}=\mathbf{0}\,\,\text{on }\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}\setminus \unicode[STIX]{x1D6E4}_{\mathit{out}}^{t}\}\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{w}\in \boldsymbol{V}^{t}=\{[H^{1}(\unicode[STIX]{x1D6FA}_{f}^{t})]^{3}:\,\boldsymbol{w}=\mathbf{0}\,\,\text{on }\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}\setminus \unicode[STIX]{x1D6E4}_{\mathit{out}}^{t}\}\end{eqnarray}$$
and
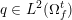 $q\in L^{2}(\unicode[STIX]{x1D6FA}_{f}^{t})$
, and where we have set
$q\in L^{2}(\unicode[STIX]{x1D6FA}_{f}^{t})$
, and where we have set
 $$\begin{eqnarray}{\mathcal{A}}_{f}^{t}(\boldsymbol{z},\boldsymbol{v},\boldsymbol{w})=\unicode[STIX]{x1D70C}_{f}\int _{\unicode[STIX]{x1D6FA}_{f}^{t}}(\boldsymbol{z}\cdot \unicode[STIX]{x1D6FB})\boldsymbol{v}\cdot \boldsymbol{w}\text{d}\unicode[STIX]{x1D714}+\unicode[STIX]{x1D707}\int _{\unicode[STIX]{x1D6FA}_{f}^{t}}(\unicode[STIX]{x1D6FB}\boldsymbol{v}+(\unicode[STIX]{x1D6FB}\boldsymbol{v})^{T}):\unicode[STIX]{x1D6FB}\boldsymbol{w}\text{d}\unicode[STIX]{x1D714}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{f}^{t}(\boldsymbol{z},\boldsymbol{v},\boldsymbol{w})=\unicode[STIX]{x1D70C}_{f}\int _{\unicode[STIX]{x1D6FA}_{f}^{t}}(\boldsymbol{z}\cdot \unicode[STIX]{x1D6FB})\boldsymbol{v}\cdot \boldsymbol{w}\text{d}\unicode[STIX]{x1D714}+\unicode[STIX]{x1D707}\int _{\unicode[STIX]{x1D6FA}_{f}^{t}}(\unicode[STIX]{x1D6FB}\boldsymbol{v}+(\unicode[STIX]{x1D6FB}\boldsymbol{v})^{T}):\unicode[STIX]{x1D6FB}\boldsymbol{w}\text{d}\unicode[STIX]{x1D714}\end{eqnarray}$$
and
 $$\begin{eqnarray}{\mathcal{B}}^{t}(q,\boldsymbol{w})=-\int _{\unicode[STIX]{x1D6FA}_{f}^{t}}q\unicode[STIX]{x1D6FB}\cdot \boldsymbol{w}\text{d}\unicode[STIX]{x1D714}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}^{t}(q,\boldsymbol{w})=-\int _{\unicode[STIX]{x1D6FA}_{f}^{t}}q\unicode[STIX]{x1D6FB}\cdot \boldsymbol{w}\text{d}\unicode[STIX]{x1D714}.\end{eqnarray}$$
The existence of a global-in-time weak solution of the above problem was proved by Leray (Reference Leray1934) for the case
 $\unicode[STIX]{x1D6FA}_{f}=\mathbb{R}^{3}$
and by Hopf (Reference Hopf1951) for the case of bounded domain. The uniqueness has been proved only for the two-dimensional case (Lions and Prodi Reference Lions and Prodi1959); for the three-dimensional case, only local-in-time uniqueness results are available (Prodi Reference Prodi1962).
$\unicode[STIX]{x1D6FA}_{f}=\mathbb{R}^{3}$
and by Hopf (Reference Hopf1951) for the case of bounded domain. The uniqueness has been proved only for the two-dimensional case (Lions and Prodi Reference Lions and Prodi1959); for the three-dimensional case, only local-in-time uniqueness results are available (Prodi Reference Prodi1962).
4.2 Mechanical wall models
The problem that models the deformation of vessel walls is given by the elastodynamics equation, which is usually written in a reference domain
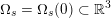 $\unicode[STIX]{x1D6FA}_{s}=\unicode[STIX]{x1D6FA}_{s}(0)\subset \mathbb{R}^{3}$
using a Lagrangian framework. For any
$\unicode[STIX]{x1D6FA}_{s}=\unicode[STIX]{x1D6FA}_{s}(0)\subset \mathbb{R}^{3}$
using a Lagrangian framework. For any
![]() $t>0$
, the material domain
$t>0$
, the material domain
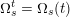 $\unicode[STIX]{x1D6FA}_{s}^{t}=\unicode[STIX]{x1D6FA}_{s}(t)$
(depicted in Figure 4.1(b)) is the image of
$\unicode[STIX]{x1D6FA}_{s}^{t}=\unicode[STIX]{x1D6FA}_{s}(t)$
(depicted in Figure 4.1(b)) is the image of
![]() $\unicode[STIX]{x1D6FA}_{s}$
by a proper Lagrangian map
$\unicode[STIX]{x1D6FA}_{s}$
by a proper Lagrangian map
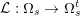 ${\mathcal{L}}:\unicode[STIX]{x1D6FA}_{s}\rightarrow \unicode[STIX]{x1D6FA}_{s}^{t}$
. We use the notation
${\mathcal{L}}:\unicode[STIX]{x1D6FA}_{s}\rightarrow \unicode[STIX]{x1D6FA}_{s}^{t}$
. We use the notation
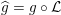 $\widehat{g}=g\circ {\mathcal{L}}$
to denote the function
$\widehat{g}=g\circ {\mathcal{L}}$
to denote the function
![]() $\widehat{g}$
induced on
$\widehat{g}$
induced on
![]() $\unicode[STIX]{x1D6FA}_{s}$
by the function
$\unicode[STIX]{x1D6FA}_{s}$
by the function
![]() $g$
defined in the current solid configuration
$g$
defined in the current solid configuration
![]() $\unicode[STIX]{x1D6FA}_{s}^{t}$
.
$\unicode[STIX]{x1D6FA}_{s}^{t}$
.
For simplicity, we assume the arterial wall obeys a (possibly non-linear) finite elastic law relating stress to strain in the arterial tissue; for more complex behaviours of arterial walls see Holzapfel, Gasser and Ogden (Reference Holzapfel, Gasser and Ogden2000) and Holzapfel and Ogden (Reference Holzapfel and Ogden2010), for example. In more realistic settings, stress is a function of the strain but also of the past loading history (Fung, Fronek and Patitucci Reference Fung, Fronek and Patitucci1979).
The problem we consider is as follows: find, at each time
![]() $t>0$
, the structure displacement
$t>0$
, the structure displacement
![]() $\boldsymbol{d}$
such that
$\boldsymbol{d}$
such that
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{s}\frac{\unicode[STIX]{x2202}^{2}\widehat{\boldsymbol{d}}}{\unicode[STIX]{x2202}t^{2}}-\unicode[STIX]{x1D6FB}\cdot \widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}})=\mathbf{0}\quad \text{in }\unicode[STIX]{x1D6FA}_{s},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{s}\frac{\unicode[STIX]{x2202}^{2}\widehat{\boldsymbol{d}}}{\unicode[STIX]{x2202}t^{2}}-\unicode[STIX]{x1D6FB}\cdot \widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}})=\mathbf{0}\quad \text{in }\unicode[STIX]{x1D6FA}_{s},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D70C}_{s}$
is the structure density. Note that volumetric forces acting in the solid domain (e.g. due to muscle forces) have been set to zero since they are quite often negligible.
$\unicode[STIX]{x1D70C}_{s}$
is the structure density. Note that volumetric forces acting in the solid domain (e.g. due to muscle forces) have been set to zero since they are quite often negligible.
The above equation is stated in terms of the first Piola–Kirchhoff tensor
![]() $\widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}})$
, which is related to the Cauchy tensor
$\widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}})$
, which is related to the Cauchy tensor
![]() $\boldsymbol{T}_{s}(\boldsymbol{d})$
via the relation
$\boldsymbol{T}_{s}(\boldsymbol{d})$
via the relation
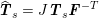 $\widehat{\boldsymbol{T}}_{s}=J\boldsymbol{T}_{s}\boldsymbol{F}^{-T}$
. Here,
$\widehat{\boldsymbol{T}}_{s}=J\boldsymbol{T}_{s}\boldsymbol{F}^{-T}$
. Here,
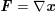 $\boldsymbol{F}=\unicode[STIX]{x1D6FB}\boldsymbol{x}$
is the deformation tensor, where the gradient is taken with respect to the reference space coordinates and
$\boldsymbol{F}=\unicode[STIX]{x1D6FB}\boldsymbol{x}$
is the deformation tensor, where the gradient is taken with respect to the reference space coordinates and
![]() $\boldsymbol{x}$
denotes point coordinates in the current configuration. Correspondingly,
$\boldsymbol{x}$
denotes point coordinates in the current configuration. Correspondingly,
 $J=\text{det}(\boldsymbol{F})$
denotes the change of volume between the reference and the current configurations; note that
$J=\text{det}(\boldsymbol{F})$
denotes the change of volume between the reference and the current configurations; note that
![]() $\boldsymbol{F}$
(and thus
$\boldsymbol{F}$
(and thus
![]() $J$
) depends on the current configuration
$J$
) depends on the current configuration
![]() $\unicode[STIX]{x1D6FA}_{s}^{t}$
.
$\unicode[STIX]{x1D6FA}_{s}^{t}$
.
For a hyperelastic material, the first Piola–Kirchhoff stress tensor is obtained by differentiating a suitable strain energy density function
![]() $\unicode[STIX]{x1D6E9}$
:
$\unicode[STIX]{x1D6E9}$
:
 $$\begin{eqnarray}\widehat{\boldsymbol{T}}_{s}=\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}{\unicode[STIX]{x2202}\boldsymbol{F}}.\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\boldsymbol{T}}_{s}=\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}}{\unicode[STIX]{x2202}\boldsymbol{F}}.\end{eqnarray}$$
Several non-linear elastic energy functions have been proposed for arteries. For the Saint Venant–Kirchhoff material,
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E9}(\boldsymbol{C}) & = & \displaystyle \frac{E\unicode[STIX]{x1D708}}{2(1+\unicode[STIX]{x1D708})(1-2\unicode[STIX]{x1D708})}\biggl(\operatorname{tr}\biggl(\frac{1}{2}(\boldsymbol{C}^{T}-\boldsymbol{I})\biggr)\biggr)^{2}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{E}{2(1+\unicode[STIX]{x1D708})}\operatorname{tr}\biggl(\biggl(\frac{1}{2}(\boldsymbol{C}^{T}-\boldsymbol{I})\biggr)^{2}\biggr),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E9}(\boldsymbol{C}) & = & \displaystyle \frac{E\unicode[STIX]{x1D708}}{2(1+\unicode[STIX]{x1D708})(1-2\unicode[STIX]{x1D708})}\biggl(\operatorname{tr}\biggl(\frac{1}{2}(\boldsymbol{C}^{T}-\boldsymbol{I})\biggr)\biggr)^{2}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{E}{2(1+\unicode[STIX]{x1D708})}\operatorname{tr}\biggl(\biggl(\frac{1}{2}(\boldsymbol{C}^{T}-\boldsymbol{I})\biggr)^{2}\biggr),\end{eqnarray}$$
where
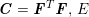 $\boldsymbol{C}=\boldsymbol{F}^{T}\boldsymbol{F},\,E$
is Young’s modulus and
$\boldsymbol{C}=\boldsymbol{F}^{T}\boldsymbol{F},\,E$
is Young’s modulus and
![]() $\unicode[STIX]{x1D708}$
is the Poisson modulus of the vessel wall. More complex and accurate functions widely used for arteries are based on separating the isotropic elastic behaviour due to the elastin and the anisotropic behaviour accounting for the stiffening increment at large displacements due to the collagen:
$\unicode[STIX]{x1D708}$
is the Poisson modulus of the vessel wall. More complex and accurate functions widely used for arteries are based on separating the isotropic elastic behaviour due to the elastin and the anisotropic behaviour accounting for the stiffening increment at large displacements due to the collagen:
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}=\unicode[STIX]{x1D6E9}^{\mathit{iso}}+\unicode[STIX]{x1D6E9}^{\mathit{aniso}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}=\unicode[STIX]{x1D6E9}^{\mathit{iso}}+\unicode[STIX]{x1D6E9}^{\mathit{aniso}}.\end{eqnarray}$$
A common choice for the isotropic part is the neo-Hookean law
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}^{\mathit{iso}}(\boldsymbol{C})=\frac{G}{2}(\operatorname{tr}(\boldsymbol{C})-3),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}^{\mathit{iso}}(\boldsymbol{C})=\frac{G}{2}(\operatorname{tr}(\boldsymbol{C})-3),\end{eqnarray}$$
whereas for the anisotropic part, an exponential law is often considered,
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}^{\mathit{aniso}}(\boldsymbol{C})=\frac{k_{1}}{2k_{2}}(\text{e}^{(k_{2}(\boldsymbol{a}\cdot (\boldsymbol{C}\boldsymbol{a})-1)^{2})}-1),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}^{\mathit{aniso}}(\boldsymbol{C})=\frac{k_{1}}{2k_{2}}(\text{e}^{(k_{2}(\boldsymbol{a}\cdot (\boldsymbol{C}\boldsymbol{a})-1)^{2})}-1),\end{eqnarray}$$
where
![]() $\boldsymbol{a}$
is the unit vector identifying the preferred direction of the collagen fibres,
$\boldsymbol{a}$
is the unit vector identifying the preferred direction of the collagen fibres,
![]() $G$
is the shear modulus, and
$G$
is the shear modulus, and
![]() $k_{1},k_{2}$
are material parameters, where
$k_{1},k_{2}$
are material parameters, where
![]() $k_{2}$
characterizes the stiffness of the material for large displacements (Fung Reference Fung1993, Holzapfel et al.
Reference Holzapfel, Gasser and Ogden2000, Raghavan and Vorp Reference Raghavan and Vorp2000). More complete laws also account for the symmetrical helical arrangement of the collagen fibres, introducing a second predominant direction of fibres (Holzapfel and Ogden Reference Holzapfel and Ogden2010). When not available from medical images, the fibre directions are computed by means of suitable algorithms under the assumption that their orientation is mainly governed by the principal stresses: see e.g. Hariton et al. (Reference Hariton, de Botton, Gasser and Holzapfel2006) and Kuhl and Holzapfel (Reference Kuhl and Holzapfel2006). For distal arteries of muscular type, viscoelastic and pseudoelastic terms are also considered (Holzapfel and Gasser Reference Holzapfel and Gasser2001).
$k_{2}$
characterizes the stiffness of the material for large displacements (Fung Reference Fung1993, Holzapfel et al.
Reference Holzapfel, Gasser and Ogden2000, Raghavan and Vorp Reference Raghavan and Vorp2000). More complete laws also account for the symmetrical helical arrangement of the collagen fibres, introducing a second predominant direction of fibres (Holzapfel and Ogden Reference Holzapfel and Ogden2010). When not available from medical images, the fibre directions are computed by means of suitable algorithms under the assumption that their orientation is mainly governed by the principal stresses: see e.g. Hariton et al. (Reference Hariton, de Botton, Gasser and Holzapfel2006) and Kuhl and Holzapfel (Reference Kuhl and Holzapfel2006). For distal arteries of muscular type, viscoelastic and pseudoelastic terms are also considered (Holzapfel and Gasser Reference Holzapfel and Gasser2001).
Sometimes the arterial tissue is modelled as being incompressible by imposing the incompressibility constraint
![]() $J=1$
on the strain energy function via Lagrange multipliers (Holzapfel Reference Holzapfel2000), that is,
$J=1$
on the strain energy function via Lagrange multipliers (Holzapfel Reference Holzapfel2000), that is,
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}^{\mathit{inc}}=\unicode[STIX]{x1D6E9}+p_{s}(J-1).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}^{\mathit{inc}}=\unicode[STIX]{x1D6E9}+p_{s}(J-1).\end{eqnarray}$$
Here
![]() $p_{s}$
is the hydrostatic pressure related to the vessel wall displacement, which plays the role of the Lagrange multiplier for the incompressibility constraint. Correspondingly, the Cauchy stress tensor is augmented as follows:
$p_{s}$
is the hydrostatic pressure related to the vessel wall displacement, which plays the role of the Lagrange multiplier for the incompressibility constraint. Correspondingly, the Cauchy stress tensor is augmented as follows:
 $$\begin{eqnarray}\boldsymbol{T}_{s}^{\mathit{inc}}(\boldsymbol{d},p_{s})=\boldsymbol{T}_{s}(\boldsymbol{d})+p_{s}\boldsymbol{I},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{T}_{s}^{\mathit{inc}}(\boldsymbol{d},p_{s})=\boldsymbol{T}_{s}(\boldsymbol{d})+p_{s}\boldsymbol{I},\end{eqnarray}$$
where
![]() $\boldsymbol{T}_{s}$
is the component arising from the energy
$\boldsymbol{T}_{s}$
is the component arising from the energy
![]() $\unicode[STIX]{x1D6E9}$
. However, experimental studies have shown that the arterial tissue in fact exhibits nearly incompressible behaviour (Carew, Vaishnav and Patel Reference Carew, Vaishnav and Patel1968). This means that the strain energy function could be decomposed into two terms
$\unicode[STIX]{x1D6E9}$
. However, experimental studies have shown that the arterial tissue in fact exhibits nearly incompressible behaviour (Carew, Vaishnav and Patel Reference Carew, Vaishnav and Patel1968). This means that the strain energy function could be decomposed into two terms
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}(\boldsymbol{C})=\unicode[STIX]{x1D6E9}_{\mathit{vol}}(J)+\unicode[STIX]{x1D6E9}_{\mathit{isoc}}(\bar{\boldsymbol{C}}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}(\boldsymbol{C})=\unicode[STIX]{x1D6E9}_{\mathit{vol}}(J)+\unicode[STIX]{x1D6E9}_{\mathit{isoc}}(\bar{\boldsymbol{C}}),\end{eqnarray}$$
where
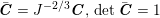 $\bar{\boldsymbol{C}}=J^{-2/3}\boldsymbol{C},\,\det \bar{\boldsymbol{C}}=1$
. The isochoric part
$\bar{\boldsymbol{C}}=J^{-2/3}\boldsymbol{C},\,\det \bar{\boldsymbol{C}}=1$
. The isochoric part
![]() $\unicode[STIX]{x1D6E9}_{\mathit{isoc}}$
is given by the general function (4.10) provided that
$\unicode[STIX]{x1D6E9}_{\mathit{isoc}}$
is given by the general function (4.10) provided that
![]() $\boldsymbol{C}$
is replaced by
$\boldsymbol{C}$
is replaced by
![]() $\bar{\boldsymbol{C}}$
and characterizes the mechanical response of the material to incompressible deformations. The volumetric part is usually given by
$\bar{\boldsymbol{C}}$
and characterizes the mechanical response of the material to incompressible deformations. The volumetric part is usually given by
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{\mathit{vol}}(J)=\frac{\unicode[STIX]{x1D705}}{2}(J-1)^{2},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{\mathit{vol}}(J)=\frac{\unicode[STIX]{x1D705}}{2}(J-1)^{2},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D705}$
(bulk modulus) is a penalty parameter to enforce the incompressibility constraint
$\unicode[STIX]{x1D705}$
(bulk modulus) is a penalty parameter to enforce the incompressibility constraint
![]() $J=1$
(Li and Robertson Reference Li and Robertson2013). In this case, the related Cauchy stress tensor is the same as in the compressible case. For a review of arterial vessel wall models we refer the reader to Holzapfel and Ogden (Reference Holzapfel and Ogden2010).
$J=1$
(Li and Robertson Reference Li and Robertson2013). In this case, the related Cauchy stress tensor is the same as in the compressible case. For a review of arterial vessel wall models we refer the reader to Holzapfel and Ogden (Reference Holzapfel and Ogden2010).
Problem (4.7) has to be completed by the initial conditions
 $$\begin{eqnarray}\boldsymbol{d}|_{t=0}=\boldsymbol{d}_{0},\quad \frac{\unicode[STIX]{x2202}\boldsymbol{d}}{\unicode[STIX]{x2202}t}\Big|_{t=0}=\boldsymbol{d}_{1}\quad \text{in }\unicode[STIX]{x1D6FA}_{s},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{d}|_{t=0}=\boldsymbol{d}_{0},\quad \frac{\unicode[STIX]{x2202}\boldsymbol{d}}{\unicode[STIX]{x2202}t}\Big|_{t=0}=\boldsymbol{d}_{1}\quad \text{in }\unicode[STIX]{x1D6FA}_{s},\end{eqnarray}$$
and boundary conditions. The latter typically prescribe on the artificial sections
![]() $\unicode[STIX]{x1D6E4}_{\mathit{artif}}^{t}$
either
$\unicode[STIX]{x1D6E4}_{\mathit{artif}}^{t}$
either
 $$\begin{eqnarray}\boldsymbol{d}=\mathbf{0}\quad \text{on }\unicode[STIX]{x1D6E4}_{\mathit{artif}}^{t}\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{d}=\mathbf{0}\quad \text{on }\unicode[STIX]{x1D6E4}_{\mathit{artif}}^{t}\end{eqnarray}$$
(fixed boundary) or
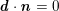 $\boldsymbol{d}\cdot \boldsymbol{n}=0$
together with
$\boldsymbol{d}\cdot \boldsymbol{n}=0$
together with
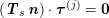 $(\boldsymbol{T}_{s}\,\boldsymbol{n})\cdot \boldsymbol{\unicode[STIX]{x1D70F}}^{(j)}=\mathbf{0}$
,
$(\boldsymbol{T}_{s}\,\boldsymbol{n})\cdot \boldsymbol{\unicode[STIX]{x1D70F}}^{(j)}=\mathbf{0}$
,
![]() $j=1,2$
, where
$j=1,2$
, where
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}^{(j)}$
are the unit tangential directions (displacement allowed in the tangential direction), whereas at the internal physical boundary
$\boldsymbol{\unicode[STIX]{x1D70F}}^{(j)}$
are the unit tangential directions (displacement allowed in the tangential direction), whereas at the internal physical boundary
![]() $\unicode[STIX]{x1D6F4}^{t}$
they prescribe the solid traction
$\unicode[STIX]{x1D6F4}^{t}$
they prescribe the solid traction
 $$\begin{eqnarray}\boldsymbol{T}_{s}\boldsymbol{n}=\boldsymbol{h}_{s}\quad \text{on }\unicode[STIX]{x1D6F4}^{t}.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{T}_{s}\boldsymbol{n}=\boldsymbol{h}_{s}\quad \text{on }\unicode[STIX]{x1D6F4}^{t}.\end{eqnarray}$$
Here
![]() $\boldsymbol{d}_{0}$
,
$\boldsymbol{d}_{0}$
,
![]() $\boldsymbol{d}_{1}$
and
$\boldsymbol{d}_{1}$
and
![]() $\boldsymbol{h}_{s}$
are suitable given functions. When considering the fluid–structure (FS) coupling,
$\boldsymbol{h}_{s}$
are suitable given functions. When considering the fluid–structure (FS) coupling,
![]() $\boldsymbol{h}_{s}$
is of course provided by the normal Cauchy stress from the fluid side: see Section 4.3. To account for the effect of the tissues surrounding the artery, the algebraic law (3.1) is often prescribed at the external lateral surface
$\boldsymbol{h}_{s}$
is of course provided by the normal Cauchy stress from the fluid side: see Section 4.3. To account for the effect of the tissues surrounding the artery, the algebraic law (3.1) is often prescribed at the external lateral surface
![]() $\unicode[STIX]{x1D6E4}_{\mathit{ext}}$
of
$\unicode[STIX]{x1D6E4}_{\mathit{ext}}$
of
![]() $\unicode[STIX]{x1D6FA}_{s}$
, to mimic the elastic behaviour of this tissue (Moireau et al.
Reference Moireau, Xiao, Astorino, Figueroa, Chapelle, Taylor and Gerbeau2012).
$\unicode[STIX]{x1D6FA}_{s}$
, to mimic the elastic behaviour of this tissue (Moireau et al.
Reference Moireau, Xiao, Astorino, Figueroa, Chapelle, Taylor and Gerbeau2012).
For each time
![]() $t>0$
, the weak form of (4.7) together with the boundary conditions (3.1), (4.14) and (4.15), in the case for fixed boundaries, reads as follows: find
$t>0$
, the weak form of (4.7) together with the boundary conditions (3.1), (4.14) and (4.15), in the case for fixed boundaries, reads as follows: find
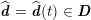 $\widehat{\boldsymbol{d}}=\widehat{\boldsymbol{d}}(t)\in \boldsymbol{D}$
,
$\widehat{\boldsymbol{d}}=\widehat{\boldsymbol{d}}(t)\in \boldsymbol{D}$
,
![]() $\widehat{\boldsymbol{d}}=\mathbf{0}$
on
$\widehat{\boldsymbol{d}}=\mathbf{0}$
on
![]() $\unicode[STIX]{x1D6E4}_{\mathit{artif}}$
,
$\unicode[STIX]{x1D6E4}_{\mathit{artif}}$
,
![]() $\widehat{\boldsymbol{d}}=\boldsymbol{d}_{0}$
and
$\widehat{\boldsymbol{d}}=\boldsymbol{d}_{0}$
and
 $\unicode[STIX]{x2202}\widehat{\boldsymbol{d}}/\unicode[STIX]{x2202}t=\boldsymbol{d}_{1}$
for
$\unicode[STIX]{x2202}\widehat{\boldsymbol{d}}/\unicode[STIX]{x2202}t=\boldsymbol{d}_{1}$
for
![]() $t=0$
in
$t=0$
in
![]() $\unicode[STIX]{x1D6FA}_{s}$
, such that
$\unicode[STIX]{x1D6FA}_{s}$
, such that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D70C}_{s}\int _{\unicode[STIX]{x1D6FA}_{s}}\frac{\unicode[STIX]{x2202}^{2}\widehat{\boldsymbol{d}}}{\unicode[STIX]{x2202}t^{2}}\cdot \widehat{\boldsymbol{e}}\text{d}\unicode[STIX]{x1D714}+\int _{\unicode[STIX]{x1D6FA}_{s}}\widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}}):\unicode[STIX]{x1D6FB}\widehat{\boldsymbol{e}}\text{d}\unicode[STIX]{x1D714}+\int _{\unicode[STIX]{x1D6E4}_{\mathit{ext}}}\unicode[STIX]{x1D6FC}_{ST}\widehat{\boldsymbol{d}}\cdot \widehat{\boldsymbol{e}}\text{d}\unicode[STIX]{x1D70E}\nonumber\\ \displaystyle & & \displaystyle \qquad =\int _{\unicode[STIX]{x1D6E4}_{\mathit{ext}}}P_{\mathit{ext}}\widehat{\boldsymbol{n}}\cdot \widehat{\boldsymbol{e}}\text{d}\unicode[STIX]{x1D70E}+\int _{\unicode[STIX]{x1D6F4}}\widehat{\boldsymbol{h}}_{s}\cdot \widehat{\boldsymbol{e}}\text{d}\unicode[STIX]{x1D70E},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D70C}_{s}\int _{\unicode[STIX]{x1D6FA}_{s}}\frac{\unicode[STIX]{x2202}^{2}\widehat{\boldsymbol{d}}}{\unicode[STIX]{x2202}t^{2}}\cdot \widehat{\boldsymbol{e}}\text{d}\unicode[STIX]{x1D714}+\int _{\unicode[STIX]{x1D6FA}_{s}}\widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}}):\unicode[STIX]{x1D6FB}\widehat{\boldsymbol{e}}\text{d}\unicode[STIX]{x1D714}+\int _{\unicode[STIX]{x1D6E4}_{\mathit{ext}}}\unicode[STIX]{x1D6FC}_{ST}\widehat{\boldsymbol{d}}\cdot \widehat{\boldsymbol{e}}\text{d}\unicode[STIX]{x1D70E}\nonumber\\ \displaystyle & & \displaystyle \qquad =\int _{\unicode[STIX]{x1D6E4}_{\mathit{ext}}}P_{\mathit{ext}}\widehat{\boldsymbol{n}}\cdot \widehat{\boldsymbol{e}}\text{d}\unicode[STIX]{x1D70E}+\int _{\unicode[STIX]{x1D6F4}}\widehat{\boldsymbol{h}}_{s}\cdot \widehat{\boldsymbol{e}}\text{d}\unicode[STIX]{x1D70E},\end{eqnarray}$$
for all
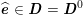 $\widehat{\boldsymbol{e}}\in \boldsymbol{D}=\boldsymbol{D}^{0}$
, where
$\widehat{\boldsymbol{e}}\in \boldsymbol{D}=\boldsymbol{D}^{0}$
, where
 $$\begin{eqnarray}\boldsymbol{D}^{t}=\{\boldsymbol{e}\in [H^{1}(\unicode[STIX]{x1D6FA}_{s}^{t})]^{3}:\,\boldsymbol{e}=\mathbf{0}\,\,\text{on }\unicode[STIX]{x1D6E4}_{\mathit{artif}}^{t}\}.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{D}^{t}=\{\boldsymbol{e}\in [H^{1}(\unicode[STIX]{x1D6FA}_{s}^{t})]^{3}:\,\boldsymbol{e}=\mathbf{0}\,\,\text{on }\unicode[STIX]{x1D6E4}_{\mathit{artif}}^{t}\}.\end{eqnarray}$$
The existence of strong (steady) solutions of the above problems could be proved using the theory developed in Ball (Reference Ball1976). For example, this is the case for the Saint Venant–Kirchhoff constitutive law given in (4.9) (Ciarlet and Necas Reference Ciarlet and Necas1985). The existence and uniqueness of weak solutions are guaranteed by the coercivity and convexity of the energy
![]() $\unicode[STIX]{x1D6E9}$
(Ciarlet Reference Ciarlet1988, Dacorogna Reference Dacorogna2000). However, a convex strain energy function is not generally able to describe instabilities such as buckling (Ball Reference Ball and Knops1977). Thus, to avoid the use of convex functions, the property of polyconvexity was introduced (Ball Reference Ball1976). Its fulfilment guarantees physically admissible solutions (Dacorogna Reference Dacorogna2000). Both the neo-Hookean law (4.11) and the exponential law (4.12) satisfy the polyconvexity property (Balzani et al.
Reference Balzani, Neff, Schroder and Holzapfel2006).
$\unicode[STIX]{x1D6E9}$
(Ciarlet Reference Ciarlet1988, Dacorogna Reference Dacorogna2000). However, a convex strain energy function is not generally able to describe instabilities such as buckling (Ball Reference Ball and Knops1977). Thus, to avoid the use of convex functions, the property of polyconvexity was introduced (Ball Reference Ball1976). Its fulfilment guarantees physically admissible solutions (Dacorogna Reference Dacorogna2000). Both the neo-Hookean law (4.11) and the exponential law (4.12) satisfy the polyconvexity property (Balzani et al.
Reference Balzani, Neff, Schroder and Holzapfel2006).
4.2.1 Modelling the structure as a 2D membrane
In some circumstances, because of the thinness of the vessel wall, a non-linear shell model has been proposed: see e.g. Leuprecht et al. (Reference Leuprecht, Perktold, Prosi, Berk, Trubel and Schima2002) and Zhao et al. (Reference Zhao, Xu, Hughes, Thom, Stanton, Ariff and Long2000). In this case, the structure problem is described by two-dimensional equations defined with respect to the middle surface, consisting of the computation of the deformation of this surface.
A simpler equation may be obtained if the structure is modelled as a 2D membrane whose position in space at any time exactly coincides with internal boundary
![]() $\unicode[STIX]{x1D6F4}^{t}$
, yielding the so-called generalized string model
$\unicode[STIX]{x1D6F4}^{t}$
, yielding the so-called generalized string model
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{s}H_{s}\frac{\unicode[STIX]{x2202}^{2}\widehat{d}_{r}}{\unicode[STIX]{x2202}t^{2}}-\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{P}\unicode[STIX]{x1D6FB}\widehat{d}_{r})+\unicode[STIX]{x1D712}H_{s}\widehat{d}_{r}=\widehat{f}_{s}\quad \text{in }\unicode[STIX]{x1D6F4}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{s}H_{s}\frac{\unicode[STIX]{x2202}^{2}\widehat{d}_{r}}{\unicode[STIX]{x2202}t^{2}}-\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{P}\unicode[STIX]{x1D6FB}\widehat{d}_{r})+\unicode[STIX]{x1D712}H_{s}\widehat{d}_{r}=\widehat{f}_{s}\quad \text{in }\unicode[STIX]{x1D6F4}\end{eqnarray}$$
(Quarteroni et al.
Reference Quarteroni, Tuveri and Veneziani2000c
). Here
![]() $\unicode[STIX]{x1D6F4}$
denotes the reference membrane configuration,
$\unicode[STIX]{x1D6F4}$
denotes the reference membrane configuration,
![]() $d_{r}$
is the radial displacement and
$d_{r}$
is the radial displacement and
![]() $H_{s}$
is the structure thickness. The tensor
$H_{s}$
is the structure thickness. The tensor
![]() $\boldsymbol{P}$
accounts for shear deformations and, possibly, for pre-stress,
$\boldsymbol{P}$
accounts for shear deformations and, possibly, for pre-stress,
 $$\begin{eqnarray}\unicode[STIX]{x1D712}=\displaystyle \frac{E}{1-\unicode[STIX]{x1D708}^{2}}(4\unicode[STIX]{x1D70C}_{1}^{2}-2(1-\unicode[STIX]{x1D708})\unicode[STIX]{x1D70C}_{2}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D712}=\displaystyle \frac{E}{1-\unicode[STIX]{x1D708}^{2}}(4\unicode[STIX]{x1D70C}_{1}^{2}-2(1-\unicode[STIX]{x1D708})\unicode[STIX]{x1D70C}_{2}),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D70C}_{1}(\boldsymbol{x})$
and
$\unicode[STIX]{x1D70C}_{1}(\boldsymbol{x})$
and
![]() $\unicode[STIX]{x1D70C}_{2}(\boldsymbol{x})$
are the mean and Gaussian curvatures of
$\unicode[STIX]{x1D70C}_{2}(\boldsymbol{x})$
are the mean and Gaussian curvatures of
![]() $\unicode[STIX]{x1D6F4}$
, respectively (Nobile and Vergara Reference Nobile and Vergara2008), and
$\unicode[STIX]{x1D6F4}$
, respectively (Nobile and Vergara Reference Nobile and Vergara2008), and
![]() $f_{s}$
is the forcing term, given by a measurement of the fluid pressure. Equation (4.17) is derived from Hooke’s law for linear elasticity under the assumptions of small thickness, plane stresses, and negligible elastic bending terms (Zienkiewicz and Taylor Reference Zienkiewicz and Taylor2005). To account for the effect of the surrounding tissue, the term
$f_{s}$
is the forcing term, given by a measurement of the fluid pressure. Equation (4.17) is derived from Hooke’s law for linear elasticity under the assumptions of small thickness, plane stresses, and negligible elastic bending terms (Zienkiewicz and Taylor Reference Zienkiewicz and Taylor2005). To account for the effect of the surrounding tissue, the term
![]() $\unicode[STIX]{x1D712}$
in (4.17) needs to be augmented by the elastic coefficient of the tissue
$\unicode[STIX]{x1D712}$
in (4.17) needs to be augmented by the elastic coefficient of the tissue
![]() $\unicode[STIX]{x1D6FC}_{ST}$
(Formaggia, Quarteroni and Vergara Reference Formaggia, Quarteroni and Vergara2013).
$\unicode[STIX]{x1D6FC}_{ST}$
(Formaggia, Quarteroni and Vergara Reference Formaggia, Quarteroni and Vergara2013).
A further simplification arises when
![]() $\unicode[STIX]{x1D6F4}$
denotes the lateral surface of a cylinder. By discarding any dependence on the circumferential coordinate, model (4.17) reduces to
$\unicode[STIX]{x1D6F4}$
denotes the lateral surface of a cylinder. By discarding any dependence on the circumferential coordinate, model (4.17) reduces to
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{s}H_{s}\frac{\unicode[STIX]{x2202}^{2}\widehat{d}_{r}}{\unicode[STIX]{x2202}t^{2}}-kGH_{s}\frac{\unicode[STIX]{x2202}^{2}\widehat{d}_{r}}{\unicode[STIX]{x2202}z^{2}}+\frac{EH_{s}}{(1-\unicode[STIX]{x1D708}^{2})R_{0}^{2}}H_{s}\widehat{d}_{r}=\widehat{f}_{s}\quad \text{in }\unicode[STIX]{x1D6F4},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{s}H_{s}\frac{\unicode[STIX]{x2202}^{2}\widehat{d}_{r}}{\unicode[STIX]{x2202}t^{2}}-kGH_{s}\frac{\unicode[STIX]{x2202}^{2}\widehat{d}_{r}}{\unicode[STIX]{x2202}z^{2}}+\frac{EH_{s}}{(1-\unicode[STIX]{x1D708}^{2})R_{0}^{2}}H_{s}\widehat{d}_{r}=\widehat{f}_{s}\quad \text{in }\unicode[STIX]{x1D6F4},\end{eqnarray}$$
where
![]() $k$
is the Timoshenko correction factor,
$k$
is the Timoshenko correction factor,
![]() $G$
is the shear modulus,
$G$
is the shear modulus,
![]() $R_{0}$
is the initial cylinder radius and
$R_{0}$
is the initial cylinder radius and
![]() $z$
is the axial coordinate. Often, in the latter case, a viscoelastic term of the form
$z$
is the axial coordinate. Often, in the latter case, a viscoelastic term of the form
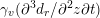 $\unicode[STIX]{x1D6FE}_{v}(\unicode[STIX]{x2202}^{3}d_{r}/\unicode[STIX]{x2202}^{2}z\unicode[STIX]{x2202}t)$
is also added, with
$\unicode[STIX]{x1D6FE}_{v}(\unicode[STIX]{x2202}^{3}d_{r}/\unicode[STIX]{x2202}^{2}z\unicode[STIX]{x2202}t)$
is also added, with
![]() $\unicode[STIX]{x1D6FE}_{v}$
denoting a suitable viscoelastic parameter (Quarteroni et al.
Reference Quarteroni, Tuveri and Veneziani2000c
).
$\unicode[STIX]{x1D6FE}_{v}$
denoting a suitable viscoelastic parameter (Quarteroni et al.
Reference Quarteroni, Tuveri and Veneziani2000c
).
4.3 The coupled fluid–structure interaction problem
Blood flow in the vessel lumen and deformation of the vessel wall are intimately connected via a fluid–structure interaction (FSI). In particular, fluid and structure interact via the fluid–structure (FS) interface
![]() $\unicode[STIX]{x1D6F4}^{t}$
which coincides with the physical fluid boundary and the internal vessel wall boundary introduced in the previous sections. The coupled problem is obtained by combining (4.1) and (4.7) at each
$\unicode[STIX]{x1D6F4}^{t}$
which coincides with the physical fluid boundary and the internal vessel wall boundary introduced in the previous sections. The coupled problem is obtained by combining (4.1) and (4.7) at each
![]() $t>0$
, as follows:
$t>0$
, as follows:
 $$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D70C}_{f}\biggl(\frac{\unicode[STIX]{x2202}\boldsymbol{v}}{\unicode[STIX]{x2202}t}+(\boldsymbol{v}\cdot \unicode[STIX]{x1D6FB})\boldsymbol{v}\biggr)-\unicode[STIX]{x1D6FB}\cdot \boldsymbol{T}_{f}(\boldsymbol{v},p)=\mathbf{0} & & \displaystyle \displaystyle \quad \text{in }\unicode[STIX]{x1D6FA}_{f}^{t},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D70C}_{f}\biggl(\frac{\unicode[STIX]{x2202}\boldsymbol{v}}{\unicode[STIX]{x2202}t}+(\boldsymbol{v}\cdot \unicode[STIX]{x1D6FB})\boldsymbol{v}\biggr)-\unicode[STIX]{x1D6FB}\cdot \boldsymbol{T}_{f}(\boldsymbol{v},p)=\mathbf{0} & & \displaystyle \displaystyle \quad \text{in }\unicode[STIX]{x1D6FA}_{f}^{t},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D6FB}\cdot \boldsymbol{v}=0 & & \displaystyle \displaystyle \quad \text{in }\unicode[STIX]{x1D6FA}_{f}^{t},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D6FB}\cdot \boldsymbol{v}=0 & & \displaystyle \displaystyle \quad \text{in }\unicode[STIX]{x1D6FA}_{f}^{t},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{v}=\frac{\unicode[STIX]{x2202}\boldsymbol{d}}{\unicode[STIX]{x2202}t} & & \displaystyle \displaystyle \quad \text{at }\unicode[STIX]{x1D6F4}^{t},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{v}=\frac{\unicode[STIX]{x2202}\boldsymbol{d}}{\unicode[STIX]{x2202}t} & & \displaystyle \displaystyle \quad \text{at }\unicode[STIX]{x1D6F4}^{t},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{T}_{s}(\boldsymbol{d})\,\boldsymbol{n}=\boldsymbol{T}_{f}(\boldsymbol{v},p)\,\boldsymbol{n} & & \displaystyle \displaystyle \quad \text{at }\unicode[STIX]{x1D6F4}^{t},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{T}_{s}(\boldsymbol{d})\,\boldsymbol{n}=\boldsymbol{T}_{f}(\boldsymbol{v},p)\,\boldsymbol{n} & & \displaystyle \displaystyle \quad \text{at }\unicode[STIX]{x1D6F4}^{t},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D70C}_{s}\frac{\unicode[STIX]{x2202}^{2}\widehat{\boldsymbol{d}}}{\unicode[STIX]{x2202}t^{2}}-\unicode[STIX]{x1D6FB}\cdot \widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}})=\mathbf{0} & & \displaystyle \displaystyle \quad \text{in }\unicode[STIX]{x1D6FA}_{s},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D70C}_{s}\frac{\unicode[STIX]{x2202}^{2}\widehat{\boldsymbol{d}}}{\unicode[STIX]{x2202}t^{2}}-\unicode[STIX]{x1D6FB}\cdot \widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}})=\mathbf{0} & & \displaystyle \displaystyle \quad \text{in }\unicode[STIX]{x1D6FA}_{s},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{d}_{f}=\boldsymbol{d} & & \displaystyle \displaystyle \quad \text{at }\unicode[STIX]{x1D6F4}^{t},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{d}_{f}=\boldsymbol{d} & & \displaystyle \displaystyle \quad \text{at }\unicode[STIX]{x1D6F4}^{t},\end{eqnarray}$$
For each time
![]() $t>0$
, the weak formulation of the FSI problem (4.19) together with its boundary conditions (for simplicity we set
$t>0$
, the weak formulation of the FSI problem (4.19) together with its boundary conditions (for simplicity we set
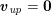 $\boldsymbol{v}_{\mathit{up}}=\mathbf{0}$
in (4.4)) reads as follows: find
$\boldsymbol{v}_{\mathit{up}}=\mathbf{0}$
in (4.4)) reads as follows: find
 $$\begin{eqnarray}\displaystyle (\boldsymbol{v}(t),\widehat{\boldsymbol{d}}(t))\in \boldsymbol{W}^{t} & = & \displaystyle \{(\boldsymbol{w},\widehat{\boldsymbol{e}})\in [H^{1}(\unicode[STIX]{x1D6FA}_{f}^{t})]^{3}\times [H^{1}(\unicode[STIX]{x1D6FA}_{s})]^{3}:\nonumber\\ \displaystyle & & \displaystyle \qquad (\boldsymbol{w},\widehat{\boldsymbol{e}})=(\mathbf{0},\mathbf{0})~\text{on}~\unicode[STIX]{x1D6E4}_{\mathit{in}}^{t}\times \unicode[STIX]{x1D6E4}_{\mathit{artif}}~\text{and}~\boldsymbol{w}=\boldsymbol{e}~\text{on}~\unicode[STIX]{x1D6F4}^{t}\},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\boldsymbol{v}(t),\widehat{\boldsymbol{d}}(t))\in \boldsymbol{W}^{t} & = & \displaystyle \{(\boldsymbol{w},\widehat{\boldsymbol{e}})\in [H^{1}(\unicode[STIX]{x1D6FA}_{f}^{t})]^{3}\times [H^{1}(\unicode[STIX]{x1D6FA}_{s})]^{3}:\nonumber\\ \displaystyle & & \displaystyle \qquad (\boldsymbol{w},\widehat{\boldsymbol{e}})=(\mathbf{0},\mathbf{0})~\text{on}~\unicode[STIX]{x1D6E4}_{\mathit{in}}^{t}\times \unicode[STIX]{x1D6E4}_{\mathit{artif}}~\text{and}~\boldsymbol{w}=\boldsymbol{e}~\text{on}~\unicode[STIX]{x1D6F4}^{t}\},\nonumber\end{eqnarray}$$
![]() $\boldsymbol{v}=\boldsymbol{v}_{0}$
for
$\boldsymbol{v}=\boldsymbol{v}_{0}$
for
![]() $t=0$
in
$t=0$
in
![]() $\unicode[STIX]{x1D6FA}_{f}$
,
$\unicode[STIX]{x1D6FA}_{f}$
,
![]() $\widehat{\boldsymbol{d}}=\boldsymbol{d}_{0}$
and
$\widehat{\boldsymbol{d}}=\boldsymbol{d}_{0}$
and
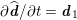 $\unicode[STIX]{x2202}\widehat{\boldsymbol{d}}/\unicode[STIX]{x2202}t=\boldsymbol{d}_{1}$
for
$\unicode[STIX]{x2202}\widehat{\boldsymbol{d}}/\unicode[STIX]{x2202}t=\boldsymbol{d}_{1}$
for
![]() $t=0$
in
$t=0$
in
![]() $\unicode[STIX]{x1D6FA}_{s}$
, and
$\unicode[STIX]{x1D6FA}_{s}$
, and
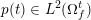 $p(t)\in L^{2}(\unicode[STIX]{x1D6FA}_{f}^{t})$
, such that
$p(t)\in L^{2}(\unicode[STIX]{x1D6FA}_{f}^{t})$
, such that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D70C}_{f}\int _{\unicode[STIX]{x1D6FA}_{f}^{t}}\frac{\unicode[STIX]{x2202}\boldsymbol{v}}{\unicode[STIX]{x2202}t}\cdot \boldsymbol{w}\text{d}\unicode[STIX]{x1D714}+{\mathcal{A}}_{f}^{t}(\boldsymbol{v},\boldsymbol{v},\boldsymbol{w})+{\mathcal{B}}^{t}(p,\boldsymbol{w})+\unicode[STIX]{x1D70C}_{s}\int _{\unicode[STIX]{x1D6FA}_{s}}\frac{\unicode[STIX]{x2202}^{2}\widehat{\boldsymbol{d}}}{\unicode[STIX]{x2202}t^{2}}\cdot \widehat{\boldsymbol{e}}\text{d}\unicode[STIX]{x1D714}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\int _{\unicode[STIX]{x1D6FA}_{s}}\widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}}):\unicode[STIX]{x1D6FB}\widehat{\boldsymbol{e}}\text{d}\unicode[STIX]{x1D714}+\int _{\unicode[STIX]{x1D6E4}_{\mathit{ext}}}\unicode[STIX]{x1D6FC}_{ST}\widehat{\boldsymbol{d}}\cdot \widehat{\boldsymbol{e}}\text{d}\unicode[STIX]{x1D70E}\nonumber\\ \displaystyle & & \displaystyle \qquad \qquad =\int _{\unicode[STIX]{x1D6E4}_{\mathit{out}}^{t}}\boldsymbol{h}_{f}\cdot \boldsymbol{n}\text{d}\unicode[STIX]{x1D6FE}+\int _{\unicode[STIX]{x1D6E4}_{\mathit{ext}}}P_{\mathit{ext}}\widehat{\boldsymbol{n}}\cdot \widehat{\boldsymbol{e}}\text{d}\unicode[STIX]{x1D70E},\nonumber\\ \displaystyle & & \displaystyle {\mathcal{B}}^{t}(q,\boldsymbol{v})=0,\nonumber\\ \displaystyle & & \displaystyle \boldsymbol{d}_{f}=\boldsymbol{d}\quad \text{at }\unicode[STIX]{x1D6F4}^{t},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D70C}_{f}\int _{\unicode[STIX]{x1D6FA}_{f}^{t}}\frac{\unicode[STIX]{x2202}\boldsymbol{v}}{\unicode[STIX]{x2202}t}\cdot \boldsymbol{w}\text{d}\unicode[STIX]{x1D714}+{\mathcal{A}}_{f}^{t}(\boldsymbol{v},\boldsymbol{v},\boldsymbol{w})+{\mathcal{B}}^{t}(p,\boldsymbol{w})+\unicode[STIX]{x1D70C}_{s}\int _{\unicode[STIX]{x1D6FA}_{s}}\frac{\unicode[STIX]{x2202}^{2}\widehat{\boldsymbol{d}}}{\unicode[STIX]{x2202}t^{2}}\cdot \widehat{\boldsymbol{e}}\text{d}\unicode[STIX]{x1D714}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\int _{\unicode[STIX]{x1D6FA}_{s}}\widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}}):\unicode[STIX]{x1D6FB}\widehat{\boldsymbol{e}}\text{d}\unicode[STIX]{x1D714}+\int _{\unicode[STIX]{x1D6E4}_{\mathit{ext}}}\unicode[STIX]{x1D6FC}_{ST}\widehat{\boldsymbol{d}}\cdot \widehat{\boldsymbol{e}}\text{d}\unicode[STIX]{x1D70E}\nonumber\\ \displaystyle & & \displaystyle \qquad \qquad =\int _{\unicode[STIX]{x1D6E4}_{\mathit{out}}^{t}}\boldsymbol{h}_{f}\cdot \boldsymbol{n}\text{d}\unicode[STIX]{x1D6FE}+\int _{\unicode[STIX]{x1D6E4}_{\mathit{ext}}}P_{\mathit{ext}}\widehat{\boldsymbol{n}}\cdot \widehat{\boldsymbol{e}}\text{d}\unicode[STIX]{x1D70E},\nonumber\\ \displaystyle & & \displaystyle {\mathcal{B}}^{t}(q,\boldsymbol{v})=0,\nonumber\\ \displaystyle & & \displaystyle \boldsymbol{d}_{f}=\boldsymbol{d}\quad \text{at }\unicode[STIX]{x1D6F4}^{t},\end{eqnarray}$$
for all
 $(\boldsymbol{w},\widehat{\boldsymbol{e}})\in \boldsymbol{W}^{t}$
and
$(\boldsymbol{w},\widehat{\boldsymbol{e}})\in \boldsymbol{W}^{t}$
and
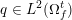 $q\in L^{2}(\unicode[STIX]{x1D6FA}_{f}^{t})$
. Note that in the above weak formulation, the two terms arising after integration by parts and involving the normal Cauchy stresses
$q\in L^{2}(\unicode[STIX]{x1D6FA}_{f}^{t})$
. Note that in the above weak formulation, the two terms arising after integration by parts and involving the normal Cauchy stresses
![]() $\boldsymbol{T}_{f}\boldsymbol{n}$
and
$\boldsymbol{T}_{f}\boldsymbol{n}$
and
![]() $\boldsymbol{T}_{s}\boldsymbol{n}$
at the interface
$\boldsymbol{T}_{s}\boldsymbol{n}$
at the interface
![]() $\unicode[STIX]{x1D6F4}^{t}$
cancel out, thanks to (4.19d
) and to the special choice of the test functions in
$\unicode[STIX]{x1D6F4}^{t}$
cancel out, thanks to (4.19d
) and to the special choice of the test functions in
![]() $\boldsymbol{W}^{t}$
.
$\boldsymbol{W}^{t}$
.
After introducing the total energy for the FSI problem, that is,
 $$\begin{eqnarray}{\mathcal{E}}_{3D}(t)=\displaystyle \frac{\unicode[STIX]{x1D70C}_{f}}{2}\int _{\unicode[STIX]{x1D6FA}_{f}^{t}}|\boldsymbol{v}|^{2}\text{d}\unicode[STIX]{x1D714}+\int _{\unicode[STIX]{x1D6FA}_{s}}\displaystyle \frac{\unicode[STIX]{x1D70C}_{s}}{2}|\dot{\widehat{\boldsymbol{d}}}|^{2}\text{d}\unicode[STIX]{x1D714}+\int _{\unicode[STIX]{x1D6FA}_{s}}\unicode[STIX]{x1D6E9}(\widehat{\boldsymbol{d}})\text{d}\unicode[STIX]{x1D714}+\int _{\unicode[STIX]{x1D6E4}_{\mathit{ext}}}\unicode[STIX]{x1D6FC}_{ST}|\widehat{\boldsymbol{d}}|^{2}\text{d}\unicode[STIX]{x1D6FE},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{E}}_{3D}(t)=\displaystyle \frac{\unicode[STIX]{x1D70C}_{f}}{2}\int _{\unicode[STIX]{x1D6FA}_{f}^{t}}|\boldsymbol{v}|^{2}\text{d}\unicode[STIX]{x1D714}+\int _{\unicode[STIX]{x1D6FA}_{s}}\displaystyle \frac{\unicode[STIX]{x1D70C}_{s}}{2}|\dot{\widehat{\boldsymbol{d}}}|^{2}\text{d}\unicode[STIX]{x1D714}+\int _{\unicode[STIX]{x1D6FA}_{s}}\unicode[STIX]{x1D6E9}(\widehat{\boldsymbol{d}})\text{d}\unicode[STIX]{x1D714}+\int _{\unicode[STIX]{x1D6E4}_{\mathit{ext}}}\unicode[STIX]{x1D6FC}_{ST}|\widehat{\boldsymbol{d}}|^{2}\text{d}\unicode[STIX]{x1D6FE},\end{eqnarray}$$
the following conservation property holds true for the case of homogeneous boundary conditions:
 $$\begin{eqnarray}\frac{\text{d}}{\text{d}t}{\mathcal{E}}_{3D}(t)+\frac{\unicode[STIX]{x1D707}}{2}\int _{\unicode[STIX]{x1D6FA}_{f}^{t}}(\unicode[STIX]{x1D6FB}\boldsymbol{v}+(\unicode[STIX]{x1D6FB}\boldsymbol{v})^{t})^{2}\text{d}\unicode[STIX]{x1D714}=0\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}}{\text{d}t}{\mathcal{E}}_{3D}(t)+\frac{\unicode[STIX]{x1D707}}{2}\int _{\unicode[STIX]{x1D6FA}_{f}^{t}}(\unicode[STIX]{x1D6FB}\boldsymbol{v}+(\unicode[STIX]{x1D6FB}\boldsymbol{v})^{t})^{2}\text{d}\unicode[STIX]{x1D714}=0\end{eqnarray}$$
(Formaggia et al. Reference Formaggia, Gerbeau, Nobile and Quarteroni2001, Reference Formaggia, Quarteroni and Vergara2013).
When the membrane model (4.17) is used instead of (4.19e ), the matching conditions (4.19c , 4.19d ) are replaced by
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}ll@{}}\displaystyle \boldsymbol{v}\cdot \boldsymbol{n}=\frac{\unicode[STIX]{x2202}d_{r}}{\unicode[STIX]{x2202}t} & \displaystyle \text{at }\unicode[STIX]{x1D6F4}^{t},\\ \displaystyle \boldsymbol{T}_{f}(\boldsymbol{v},p)\boldsymbol{n}\cdot \boldsymbol{n}=-f_{s} & \displaystyle \text{at }\unicode[STIX]{x1D6F4}^{t},\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}ll@{}}\displaystyle \boldsymbol{v}\cdot \boldsymbol{n}=\frac{\unicode[STIX]{x2202}d_{r}}{\unicode[STIX]{x2202}t} & \displaystyle \text{at }\unicode[STIX]{x1D6F4}^{t},\\ \displaystyle \boldsymbol{T}_{f}(\boldsymbol{v},p)\boldsymbol{n}\cdot \boldsymbol{n}=-f_{s} & \displaystyle \text{at }\unicode[STIX]{x1D6F4}^{t},\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
where
![]() $d_{r}$
is the membrane displacement written in the current configuration and
$d_{r}$
is the membrane displacement written in the current configuration and
![]() $f_{s}$
is the forcing term of the membrane equation (see (4.17)), acting only at the FS interface; in this case it also plays the role of structure stress exerted at the FS interface. Owing to (4.17) itself, we can rewrite the above interface conditions as follows:
$f_{s}$
is the forcing term of the membrane equation (see (4.17)), acting only at the FS interface; in this case it also plays the role of structure stress exerted at the FS interface. Owing to (4.17) itself, we can rewrite the above interface conditions as follows:
 $$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{v}\cdot \boldsymbol{n}=\frac{\unicode[STIX]{x2202}d_{r}}{\unicode[STIX]{x2202}t} & & \displaystyle \displaystyle \text{at }\unicode[STIX]{x1D6F4}^{t},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{v}\cdot \boldsymbol{n}=\frac{\unicode[STIX]{x2202}d_{r}}{\unicode[STIX]{x2202}t} & & \displaystyle \displaystyle \text{at }\unicode[STIX]{x1D6F4}^{t},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{T}_{f}(\boldsymbol{v},p)\boldsymbol{n}\cdot \boldsymbol{n}=-\biggl(\unicode[STIX]{x1D70C}_{s}H_{s}\frac{\unicode[STIX]{x2202}^{2}d_{r}}{\unicode[STIX]{x2202}t^{2}}-\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{P}\unicode[STIX]{x1D6FB}d_{r})+\unicode[STIX]{x1D712}H_{s}d_{r}\biggr) & & \displaystyle \displaystyle \text{at }\unicode[STIX]{x1D6F4}^{t}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{T}_{f}(\boldsymbol{v},p)\boldsymbol{n}\cdot \boldsymbol{n}=-\biggl(\unicode[STIX]{x1D70C}_{s}H_{s}\frac{\unicode[STIX]{x2202}^{2}d_{r}}{\unicode[STIX]{x2202}t^{2}}-\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{P}\unicode[STIX]{x1D6FB}d_{r})+\unicode[STIX]{x1D712}H_{s}d_{r}\biggr) & & \displaystyle \displaystyle \text{at }\unicode[STIX]{x1D6F4}^{t}.\end{eqnarray}$$
Figueroa et al. (Reference Figueroa, Vignon-Clementel, Jansen, Hughes and Taylor2006) propose an effective formulation to solve the FSI problem with a membrane structure, while Colciago, Deparis and Quarteroni (Reference Colciago, Deparis and Quarteroni2014) discuss the accuracy of the FSI-membrane problem in comparison to a full 3D/3D simulation. In particular, for Hooke’s law, the wall shear stresses computed with these two FSI models are in good agreement for a distal arterial tract such as a femoropopliteal bypass. In contrast, when larger displacements are considered such as in the ascending aorta, the discrepancies between the two FSI models increase.
4.4 The boundary issue
According to the mathematical theory of the incompressible Navier–Stokes equations, three scalar conditions need to be prescribed at each point of the boundary. This, however, is seldom realistic in clinical practice. For instance, PC-MRA provides velocity data, but this technique is not routinely used and ad hoc studies are required (Morbiducci et al.
Reference Morbiducci, Ponzini, Rizzo, Cadioli, Esposito, De Cobelli, Del Maschio, Montevecchi and Redaelli2009). Alternatively, the flow rate
 $Q=Q(t)$
can be obtained across a boundary cross-section
$Q=Q(t)$
can be obtained across a boundary cross-section
![]() $\unicode[STIX]{x1D6E4}^{t}$
, by suitable postprocessing of data retrieved by echo-colour-Doppler or by thermal images: see Section 3.2. This yields the flow rate condition (3.2). In other situations, at both the inlet and outlet cross-sections, pressure measurements
$\unicode[STIX]{x1D6E4}^{t}$
, by suitable postprocessing of data retrieved by echo-colour-Doppler or by thermal images: see Section 3.2. This yields the flow rate condition (3.2). In other situations, at both the inlet and outlet cross-sections, pressure measurements
 $P=P(t)$
may be considered as representative of an average estimate, leading to condition (3.3).
$P=P(t)$
may be considered as representative of an average estimate, leading to condition (3.3).
From a mathematical perspective, (3.2) and (3.3) are defective conditions as they prescribe only one scalar function over the entire section
![]() $\unicode[STIX]{x1D6E4}^{t}$
(Formaggia et al.
Reference Formaggia, Gerbeau, Nobile and Quarteroni2002). Several strategies have been proposed so far to supplement (3.2) or (3.3) with other conditions that allow us to ‘close’ the system. For clarity, we can classify them according to three different strategies, which are reported below.
$\unicode[STIX]{x1D6E4}^{t}$
(Formaggia et al.
Reference Formaggia, Gerbeau, Nobile and Quarteroni2002). Several strategies have been proposed so far to supplement (3.2) or (3.3) with other conditions that allow us to ‘close’ the system. For clarity, we can classify them according to three different strategies, which are reported below.
4.4.1 Conjecturing velocity and pressure profiles
A common trick to effectively prescribe the flow rate condition (3.2) consists in prescribing a velocity profile
 $$\begin{eqnarray}\boldsymbol{v}(t)=\boldsymbol{g}(t)\quad \text{on }\unicode[STIX]{x1D6E4}^{t},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{v}(t)=\boldsymbol{g}(t)\quad \text{on }\unicode[STIX]{x1D6E4}^{t},\end{eqnarray}$$
where
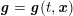 $\boldsymbol{g}=\boldsymbol{g}(t,\boldsymbol{x})$
is chosen in such a way as to satisfy (3.2), that is,
$\boldsymbol{g}=\boldsymbol{g}(t,\boldsymbol{x})$
is chosen in such a way as to satisfy (3.2), that is,
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{f}\int _{\unicode[STIX]{x1D6E4}^{t}}\boldsymbol{g}(t)\cdot \boldsymbol{n}\text{d}\unicode[STIX]{x1D6FE}=Q(t).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{f}\int _{\unicode[STIX]{x1D6E4}^{t}}\boldsymbol{g}(t)\cdot \boldsymbol{n}\text{d}\unicode[STIX]{x1D6FE}=Q(t).\end{eqnarray}$$
The flow rate condition (3.2) is therefore replaced with the standard (vectorial) Dirichlet condition (4.24). A classical choice for
![]() $\boldsymbol{g}$
is a parabolic profile (e.g. for flow simulations in the carotid arteries: Campbell et al. Reference Campbell, Ries, Dhawan, Quyyumi, Taylor and Oshinski2012), a constant profile (often used for the ascending aorta: Moireau et al. Reference Moireau, Xiao, Astorino, Figueroa, Chapelle, Taylor and Gerbeau2012), or that obtained from the Womersley solution (He, Ku and Moore Reference He, Ku and Moore1993). Both the parabolic and Womersley profiles require a circular section to be prescribed, while non-circular sections require an appropriate morphing (He et al.
Reference He, Ku and Moore1993).
$\boldsymbol{g}$
is a parabolic profile (e.g. for flow simulations in the carotid arteries: Campbell et al. Reference Campbell, Ries, Dhawan, Quyyumi, Taylor and Oshinski2012), a constant profile (often used for the ascending aorta: Moireau et al. Reference Moireau, Xiao, Astorino, Figueroa, Chapelle, Taylor and Gerbeau2012), or that obtained from the Womersley solution (He, Ku and Moore Reference He, Ku and Moore1993). Both the parabolic and Womersley profiles require a circular section to be prescribed, while non-circular sections require an appropriate morphing (He et al.
Reference He, Ku and Moore1993).
In spite of its straightforward implementation, this choice has a major impact on the solution, particularly in the neighbourhood of the section
![]() $\unicode[STIX]{x1D6E4}^{t}$
and for elevated values of the Reynolds number (Veneziani and Vergara Reference Veneziani and Vergara2007). To reduce the sensitivity to the arbitrary choice of the profile, the computational domain can be artificially elongated by operating what is called a flow extension (Moore, Steinman and Ethier Reference Moore, Steinman and Ethier1997).
$\unicode[STIX]{x1D6E4}^{t}$
and for elevated values of the Reynolds number (Veneziani and Vergara Reference Veneziani and Vergara2007). To reduce the sensitivity to the arbitrary choice of the profile, the computational domain can be artificially elongated by operating what is called a flow extension (Moore, Steinman and Ethier Reference Moore, Steinman and Ethier1997).
A similar approach could be applied to the mean normal Cauchy stress condition (3.3) as well. In the case at hand, we can postulate that the pressure on
![]() $\unicode[STIX]{x1D6E4}^{t}$
is constant and that the viscous stress can be neglected, that is, we can prescribe
$\unicode[STIX]{x1D6E4}^{t}$
is constant and that the viscous stress can be neglected, that is, we can prescribe
 $$\begin{eqnarray}p\boldsymbol{n}-\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FB}\boldsymbol{v}+(\unicode[STIX]{x1D6FB}\boldsymbol{v})^{T})\,\boldsymbol{n}=P\boldsymbol{n}\quad \text{on }\unicode[STIX]{x1D6E4}^{t}.\end{eqnarray}$$
$$\begin{eqnarray}p\boldsymbol{n}-\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FB}\boldsymbol{v}+(\unicode[STIX]{x1D6FB}\boldsymbol{v})^{T})\,\boldsymbol{n}=P\boldsymbol{n}\quad \text{on }\unicode[STIX]{x1D6E4}^{t}.\end{eqnarray}$$
Note that the above condition in particular satisfies the defective condition (3.3). Condition (4.26) is generally acceptable because the pressure changes in arteries mainly occur along the axial direction and the viscous stresses are negligible on orthogonal cross-sections.
Since
![]() $P\boldsymbol{n}$
plays the role of boundary normal Cauchy stress when implemented in the framework of finite element approximations, no further action is required beyond assembling the matrix for Neumann conditions. For this reason, the treatment has been called the ‘do-nothing’ approach (Heywood et al.
Reference Heywood, Rannacher and Turek1996). As pointed out by Veneziani Reference Veneziani and Rannacher1998a
, Reference Veneziani1998b
, this procedure is in fact not completely ‘innocent’. The do-nothing approach corresponds to the following weak formulation (for simplicity we assume homogeneous Dirichlet conditions,
$P\boldsymbol{n}$
plays the role of boundary normal Cauchy stress when implemented in the framework of finite element approximations, no further action is required beyond assembling the matrix for Neumann conditions. For this reason, the treatment has been called the ‘do-nothing’ approach (Heywood et al.
Reference Heywood, Rannacher and Turek1996). As pointed out by Veneziani Reference Veneziani and Rannacher1998a
, Reference Veneziani1998b
, this procedure is in fact not completely ‘innocent’. The do-nothing approach corresponds to the following weak formulation (for simplicity we assume homogeneous Dirichlet conditions,
 $\boldsymbol{v}_{\mathit{up}}=\mathbf{0}$
): for each
$\boldsymbol{v}_{\mathit{up}}=\mathbf{0}$
): for each
![]() $t>0$
, find
$t>0$
, find
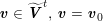 $\boldsymbol{v}\in \widetilde{\boldsymbol{V}}^{t},\,\boldsymbol{v}=\boldsymbol{v}_{0}$
– chk for
$\boldsymbol{v}\in \widetilde{\boldsymbol{V}}^{t},\,\boldsymbol{v}=\boldsymbol{v}_{0}$
– chk for
![]() $t=0$
in
$t=0$
in
![]() $\unicode[STIX]{x1D6FA}_{f}$
, and
$\unicode[STIX]{x1D6FA}_{f}$
, and
 $p\in L^{2}(\unicode[STIX]{x1D6FA}_{f}^{t})$
such that
$p\in L^{2}(\unicode[STIX]{x1D6FA}_{f}^{t})$
such that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D70C}_{f}\int _{\unicode[STIX]{x1D6FA}_{f}^{t}}\frac{\unicode[STIX]{x2202}\boldsymbol{v}}{\unicode[STIX]{x2202}t}\cdot \boldsymbol{w}\text{d}\unicode[STIX]{x1D714}+{\mathcal{A}}_{f}^{t}(\boldsymbol{v},\boldsymbol{v},\boldsymbol{w})+{\mathcal{B}}^{t}(p,\boldsymbol{w})\nonumber\\ \displaystyle & & \displaystyle \qquad =\int _{\unicode[STIX]{x1D6E4}_{\mathit{out}}^{t}}\boldsymbol{h}_{f}\cdot \boldsymbol{n}\text{d}\unicode[STIX]{x1D6FE}-P\int _{\unicode[STIX]{x1D6E4}^{t}}\boldsymbol{w}\cdot \boldsymbol{n}\text{d}\unicode[STIX]{x1D6FE},\nonumber\\ \displaystyle & & \displaystyle {\mathcal{B}}^{t}(q,\boldsymbol{v})=0,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D70C}_{f}\int _{\unicode[STIX]{x1D6FA}_{f}^{t}}\frac{\unicode[STIX]{x2202}\boldsymbol{v}}{\unicode[STIX]{x2202}t}\cdot \boldsymbol{w}\text{d}\unicode[STIX]{x1D714}+{\mathcal{A}}_{f}^{t}(\boldsymbol{v},\boldsymbol{v},\boldsymbol{w})+{\mathcal{B}}^{t}(p,\boldsymbol{w})\nonumber\\ \displaystyle & & \displaystyle \qquad =\int _{\unicode[STIX]{x1D6E4}_{\mathit{out}}^{t}}\boldsymbol{h}_{f}\cdot \boldsymbol{n}\text{d}\unicode[STIX]{x1D6FE}-P\int _{\unicode[STIX]{x1D6E4}^{t}}\boldsymbol{w}\cdot \boldsymbol{n}\text{d}\unicode[STIX]{x1D6FE},\nonumber\\ \displaystyle & & \displaystyle {\mathcal{B}}^{t}(q,\boldsymbol{v})=0,\nonumber\end{eqnarray}$$
for all
 $$\begin{eqnarray}\boldsymbol{w}\in \widetilde{\boldsymbol{V}}^{t}=\{[H^{1}(\unicode[STIX]{x1D6FA}_{f}^{t})]^{3}:\,\boldsymbol{w}=\mathbf{0}\quad \text{on }\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}\setminus (\unicode[STIX]{x1D6E4}_{\mathit{out}}^{t}\cup \unicode[STIX]{x1D6E4}^{t})\}\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{w}\in \widetilde{\boldsymbol{V}}^{t}=\{[H^{1}(\unicode[STIX]{x1D6FA}_{f}^{t})]^{3}:\,\boldsymbol{w}=\mathbf{0}\quad \text{on }\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}\setminus (\unicode[STIX]{x1D6E4}_{\mathit{out}}^{t}\cup \unicode[STIX]{x1D6E4}^{t})\}\end{eqnarray}$$
and
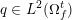 $q\in L^{2}(\unicode[STIX]{x1D6FA}_{f}^{t})$
.
$q\in L^{2}(\unicode[STIX]{x1D6FA}_{f}^{t})$
.
A do-nothing formulation for the flow rate conditions is possible too: see Heywood et al. (Reference Heywood, Rannacher and Turek1996) and Veneziani (Reference Veneziani1998b ).
Note that as an alternative to (3.3), other defective conditions involving the fluid pressure could be considered as well. This is the case for mean pressure conditions (Heywood et al.
Reference Heywood, Rannacher and Turek1996), or conditions involving the total pressure (Formaggia et al.
Reference Formaggia, Quarteroni and Vergara2013), defined by
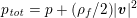 $p_{\mathit{tot}}=p+(\unicode[STIX]{x1D70C}_{f}/2)|\boldsymbol{v}|^{2}$
. For a comprehensive review of these conditions, we refer the interested reader to Quarteroni et al. (Reference Quarteroni, Veneziani and Vergara2016c
).
$p_{\mathit{tot}}=p+(\unicode[STIX]{x1D70C}_{f}/2)|\boldsymbol{v}|^{2}$
. For a comprehensive review of these conditions, we refer the interested reader to Quarteroni et al. (Reference Quarteroni, Veneziani and Vergara2016c
).
4.4.2 Augmented formulation
An alternative approach is to regard the flow rate boundary condition (3.2) as a constraint for the solution of the fluid problem and then enforce it via a Lagrange multiplier approach. As a scalar constraint, we need a scalar multiplier
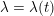 $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}(t)$
at each time, resulting in the following weak formulation (we again consider the case of homogeneous Dirichlet conditions): for each
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}(t)$
at each time, resulting in the following weak formulation (we again consider the case of homogeneous Dirichlet conditions): for each
![]() $t>0$
, find
$t>0$
, find
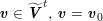 $\boldsymbol{v}\in \widetilde{\boldsymbol{V}}^{t},\,\boldsymbol{v}=\boldsymbol{v}_{0}$
for
$\boldsymbol{v}\in \widetilde{\boldsymbol{V}}^{t},\,\boldsymbol{v}=\boldsymbol{v}_{0}$
for
![]() $t=0$
in
$t=0$
in
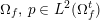 $\unicode[STIX]{x1D6FA}_{f},\,p\in L^{2}(\unicode[STIX]{x1D6FA}_{f}^{t})$
, and
$\unicode[STIX]{x1D6FA}_{f},\,p\in L^{2}(\unicode[STIX]{x1D6FA}_{f}^{t})$
, and
![]() $\unicode[STIX]{x1D706}\in \mathbb{R}$
such that
$\unicode[STIX]{x1D706}\in \mathbb{R}$
such that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D70C}_{f}\int _{\unicode[STIX]{x1D6FA}_{f}^{t}}\frac{\unicode[STIX]{x2202}\boldsymbol{v}}{\unicode[STIX]{x2202}t}\cdot \boldsymbol{w}\text{d}\unicode[STIX]{x1D714}+{\mathcal{A}}_{f}^{t}(\boldsymbol{v},\boldsymbol{v},\boldsymbol{w})+{\mathcal{B}}^{t}(p,\boldsymbol{w})+{\mathcal{C}}^{t}(\unicode[STIX]{x1D706},\boldsymbol{w})=\int _{\unicode[STIX]{x1D6E4}_{\mathit{out}}^{t}}\boldsymbol{h}_{f}\cdot \boldsymbol{w}\text{d}\unicode[STIX]{x1D6FE},\nonumber\\ \displaystyle & & \displaystyle \displaystyle {\mathcal{B}}^{t}(q,\boldsymbol{v})=0,\nonumber\\ \displaystyle & & \displaystyle \displaystyle {\mathcal{C}}^{t}(\unicode[STIX]{x1D713},\boldsymbol{v})=\unicode[STIX]{x1D713}\,\frac{Q}{\unicode[STIX]{x1D70C}_{f}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D70C}_{f}\int _{\unicode[STIX]{x1D6FA}_{f}^{t}}\frac{\unicode[STIX]{x2202}\boldsymbol{v}}{\unicode[STIX]{x2202}t}\cdot \boldsymbol{w}\text{d}\unicode[STIX]{x1D714}+{\mathcal{A}}_{f}^{t}(\boldsymbol{v},\boldsymbol{v},\boldsymbol{w})+{\mathcal{B}}^{t}(p,\boldsymbol{w})+{\mathcal{C}}^{t}(\unicode[STIX]{x1D706},\boldsymbol{w})=\int _{\unicode[STIX]{x1D6E4}_{\mathit{out}}^{t}}\boldsymbol{h}_{f}\cdot \boldsymbol{w}\text{d}\unicode[STIX]{x1D6FE},\nonumber\\ \displaystyle & & \displaystyle \displaystyle {\mathcal{B}}^{t}(q,\boldsymbol{v})=0,\nonumber\\ \displaystyle & & \displaystyle \displaystyle {\mathcal{C}}^{t}(\unicode[STIX]{x1D713},\boldsymbol{v})=\unicode[STIX]{x1D713}\,\frac{Q}{\unicode[STIX]{x1D70C}_{f}},\end{eqnarray}$$
for all
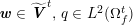 $\boldsymbol{w}\in \widetilde{\boldsymbol{V}}^{t},\,q\in L^{2}(\unicode[STIX]{x1D6FA}_{f}^{t})$
, and
$\boldsymbol{w}\in \widetilde{\boldsymbol{V}}^{t},\,q\in L^{2}(\unicode[STIX]{x1D6FA}_{f}^{t})$
, and
![]() $\unicode[STIX]{x1D713}\in \mathbb{R}$
, and where we have set
$\unicode[STIX]{x1D713}\in \mathbb{R}$
, and where we have set
 $$\begin{eqnarray}{\mathcal{C}}^{t}(\unicode[STIX]{x1D713},\boldsymbol{w})=\unicode[STIX]{x1D713}\int _{\unicode[STIX]{x1D6E4}^{t}}\boldsymbol{w}\cdot \boldsymbol{n}\text{d}\unicode[STIX]{x1D6FE}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{C}}^{t}(\unicode[STIX]{x1D713},\boldsymbol{w})=\unicode[STIX]{x1D713}\int _{\unicode[STIX]{x1D6E4}^{t}}\boldsymbol{w}\cdot \boldsymbol{n}\text{d}\unicode[STIX]{x1D6FE}.\end{eqnarray}$$
See Formaggia et al. (Reference Formaggia, Gerbeau, Nobile and Quarteroni2002) and Veneziani and Vergara (Reference Veneziani and Vergara2005), who also analyse the well-posedness of this problem.
Besides prescribing the flow rate condition (3.2), the above augmented formulation enforces at each time a constant-in-space normal Cauchy stress on
![]() $\unicode[STIX]{x1D6E4}^{t}$
aligned with its normal direction, which precisely coincides with the Lagrange multiplier
$\unicode[STIX]{x1D6E4}^{t}$
aligned with its normal direction, which precisely coincides with the Lagrange multiplier
![]() $\unicode[STIX]{x1D706}$
, that is,
$\unicode[STIX]{x1D706}$
, that is,
 $$\begin{eqnarray}-p\boldsymbol{n}+\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FB}\boldsymbol{u}+(\unicode[STIX]{x1D6FB}\boldsymbol{v})^{T})\,\boldsymbol{n}=\unicode[STIX]{x1D706}\boldsymbol{n}\quad \text{on }\unicode[STIX]{x1D6E4}^{t}.\end{eqnarray}$$
$$\begin{eqnarray}-p\boldsymbol{n}+\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FB}\boldsymbol{u}+(\unicode[STIX]{x1D6FB}\boldsymbol{v})^{T})\,\boldsymbol{n}=\unicode[STIX]{x1D706}\boldsymbol{n}\quad \text{on }\unicode[STIX]{x1D6E4}^{t}.\end{eqnarray}$$
This method is particularly suitable when the artificial cross-section is orthogonal to the longitudinal axis, so that vector
![]() $\boldsymbol{n}$
is truly aligned along the axial direction.
$\boldsymbol{n}$
is truly aligned along the axial direction.
Since the velocity spatial profile is not prescribed a priori, this technique has been used to improve the parabolic-based law implemented in the Doppler technology for the estimation of the flow rate starting from the peak velocity (Ponzini et al. Reference Ponzini, Vergara, Redaelli and Veneziani2006, Vergara et al. Reference Vergara, Ponzini, Veneziani, Redaelli, Neglia and Parodi2010, Ponzini et al. Reference Ponzini, Vergara, Rizzo, Veneziani, Roghi, Vanzulli, Parodi and Redaelli2010).
Extension of the augmented formulation to the case of compliant walls is addressed in Formaggia, Veneziani and Vergara (Reference Formaggia, Veneziani and Vergara2009b ) and to the quasi-Newtonian case in Ervin and Lee (Reference Ervin and Lee2007).
An augmented formulation has been proposed by Formaggia et al. (Reference Formaggia, Gerbeau, Nobile and Quarteroni2002) to prescribe condition (3.3) as well. However, as noticed by Formaggia et al. (Reference Formaggia, Gerbeau, Nobile and Quarteroni2002), in this case it yields at each time the condition
 $$\begin{eqnarray}\boldsymbol{v}=\unicode[STIX]{x1D706}\boldsymbol{n}\quad \text{at }\unicode[STIX]{x1D6E4}^{t},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{v}=\unicode[STIX]{x1D706}\boldsymbol{n}\quad \text{at }\unicode[STIX]{x1D6E4}^{t},\end{eqnarray}$$
where
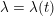 $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}(t)$
is again the constant-in-space Lagrange multiplier. This is a non-homogeneous Dirichlet boundary condition for the fluid velocity, which is generally incompatible with the no-slip condition
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}(t)$
is again the constant-in-space Lagrange multiplier. This is a non-homogeneous Dirichlet boundary condition for the fluid velocity, which is generally incompatible with the no-slip condition
![]() $\boldsymbol{v}=\boldsymbol{\unicode[STIX]{x1D719}}$
prescribed at the physical boundary
$\boldsymbol{v}=\boldsymbol{\unicode[STIX]{x1D719}}$
prescribed at the physical boundary
![]() $\unicode[STIX]{x1D6F4}^{t}$
. For this reason, the approach is no longer used.
$\unicode[STIX]{x1D6F4}^{t}$
. For this reason, the approach is no longer used.
4.4.3 A control-based approach
A different strategy for the fulfilment of condition (3.2) is based on the minimization of the mismatch functional
 $$\begin{eqnarray}J(\boldsymbol{v})=\frac{1}{2}\biggl(\int _{\unicode[STIX]{x1D6E4}^{t}}\boldsymbol{v}\cdot \boldsymbol{n}\text{d}\unicode[STIX]{x1D6FE}-Q\biggr)^{2},\end{eqnarray}$$
$$\begin{eqnarray}J(\boldsymbol{v})=\frac{1}{2}\biggl(\int _{\unicode[STIX]{x1D6E4}^{t}}\boldsymbol{v}\cdot \boldsymbol{n}\text{d}\unicode[STIX]{x1D6FE}-Q\biggr)^{2},\end{eqnarray}$$
constrained by the fact that
![]() $\boldsymbol{v}$
satisfies the incompressible Navier–Stokes equations (Formaggia, Veneziani and Vergara Reference Formaggia, Veneziani and Vergara2008). This PDE-constrained optimization – which can be regarded as the dual of the above augmented strategy – yields a system of optimality conditions to be fulfilled (also referred to as the Karush–Kuhn–Tucker (KKT) system): see Section 9.1.2 for further details. In particular, Formaggia et al. (Reference Formaggia, Veneziani and Vergara2008) used the normal component of the normal Cauchy stress on
$\boldsymbol{v}$
satisfies the incompressible Navier–Stokes equations (Formaggia, Veneziani and Vergara Reference Formaggia, Veneziani and Vergara2008). This PDE-constrained optimization – which can be regarded as the dual of the above augmented strategy – yields a system of optimality conditions to be fulfilled (also referred to as the Karush–Kuhn–Tucker (KKT) system): see Section 9.1.2 for further details. In particular, Formaggia et al. (Reference Formaggia, Veneziani and Vergara2008) used the normal component of the normal Cauchy stress on
![]() $\unicode[STIX]{x1D6E4}^{t}$
as the control variable for the minimization of the mismatch functional. This approach was considered by Formaggia et al. (Reference Formaggia, Veneziani and Vergara2009b
) for the compliant case, whereas Lee (Reference Lee2011), Galvin and Lee (Reference Galvin and Lee2013) and Galvin, Lee and Rebholz (Reference Galvin, Lee and Rebholz2012) address the non-Newtonian, quasi-Newtonian and viscoelastic cases.
$\unicode[STIX]{x1D6E4}^{t}$
as the control variable for the minimization of the mismatch functional. This approach was considered by Formaggia et al. (Reference Formaggia, Veneziani and Vergara2009b
) for the compliant case, whereas Lee (Reference Lee2011), Galvin and Lee (Reference Galvin and Lee2013) and Galvin, Lee and Rebholz (Reference Galvin, Lee and Rebholz2012) address the non-Newtonian, quasi-Newtonian and viscoelastic cases.
The same approach can also be used to fulfil the defective condition (3.3) provided that a suitable functional to be minimized is introduced (Formaggia et al. Reference Formaggia, Veneziani and Vergara2008). This allows us to prescribe (3.3) on a section oblique with respect to the longitudinal axis too. In this case the control variable is the complete normal Cauchy stress vector, that is, the direction of the normal Cauchy stress is also a priori unknown.
Boundary data may also be lacking for the cross-section of the vessel wall. In this case we end up with defective BC issues for the vessel wall: see e.g. Quarteroni et al. (Reference Quarteroni, Veneziani and Vergara2016c ).
4.5 Geometric reduced models and the geometric multiscale approach
4.5.1 The 1D and 0D models
Numerical modelling of the entire cardiovascular system by means of 3D models is currently not affordable because of the complexity of the computational domain, which is composed of thousands of arteries and veins and billions of arterioles, capillaries and venules (Nichols and O’Rourke Reference Nichols and O’Rourke2005). In many applications, reduced-dimensional models are used instead, either as stand-alone models or coupled with the 3D ones.
The first one-dimensional (1D) model was introduced almost 250 years ago by Euler (Reference Euler1775). Subsequently this approach was brought into the engineering environment by Barnard et al. (Reference Barnard, Hunt, Timlake and Varley1966), Hughes (Reference Hughes1974) and Hughes and Lubliner (Reference Hughes and Lubliner1973). These models allow the description of blood flow in a compliant vessel where the only space coordinate is that of the vessel axis.
One-dimensional models may be derived from 3D models by making simplifying assumptions on the behaviour of the flow, the structure, and their interaction (Quarteroni and Formaggia Reference Quarteroni and Formaggia2004, Peiró and Veneziani Reference Peiró, Veneziani, Quarteroni, Formaggia and Veneziani2009). The starting fluid domain is a truncated cone: see Figure 4.2. Referring to cylindrical coordinates
![]() $(r,\unicode[STIX]{x1D711},z)$
, we make the following simplifying assumptions: (i) the axis of the cylinder is fixed; (ii) for any
$(r,\unicode[STIX]{x1D711},z)$
, we make the following simplifying assumptions: (i) the axis of the cylinder is fixed; (ii) for any
![]() $z$
, the cross-section
$z$
, the cross-section
![]() ${\mathcal{S}}(t,z)$
is a circle with radius
${\mathcal{S}}(t,z)$
is a circle with radius
![]() $R(t,z)$
; (iii) the solution of both fluid and structure problems does not depend on
$R(t,z)$
; (iii) the solution of both fluid and structure problems does not depend on
![]() $\unicode[STIX]{x1D711}$
; (iv) the pressure is constant over each section
$\unicode[STIX]{x1D711}$
; (iv) the pressure is constant over each section
![]() ${\mathcal{S}}(t,z)$
; (v) the axial fluid velocity
${\mathcal{S}}(t,z)$
; (v) the axial fluid velocity
![]() $v_{z}$
dominates the other velocity components; (vi) only radial displacements are allowed, so the structure deformation takes the form
$v_{z}$
dominates the other velocity components; (vi) only radial displacements are allowed, so the structure deformation takes the form
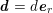 $\boldsymbol{d}=d\boldsymbol{e}_{r}$
, where
$\boldsymbol{d}=d\boldsymbol{e}_{r}$
, where
![]() $\boldsymbol{e}_{r}$
is the unit vector in the radial direction, and
$\boldsymbol{e}_{r}$
is the unit vector in the radial direction, and
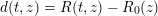 $d(t,z)=R(t,z)-R_{0}(z)$
, where
$d(t,z)=R(t,z)-R_{0}(z)$
, where
![]() $R_{0}(z)$
is the reference radius at the equilibrium; (vii) the fluid is assumed to obey Poiseuille’s law, so that the viscous effects are modelled by a linear term proportional to the flow rate; (viii) the vessel structure is modelled as a membrane with constant thickness.
$R_{0}(z)$
is the reference radius at the equilibrium; (vii) the fluid is assumed to obey Poiseuille’s law, so that the viscous effects are modelled by a linear term proportional to the flow rate; (viii) the vessel structure is modelled as a membrane with constant thickness.

Figure 4.2. Fluid domain for the derivation of the 1D model.
We introduce the following quantities:
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}ll@{}}\displaystyle A(t,z)=|{\mathcal{S}}(t,z)|=\unicode[STIX]{x1D70B}R(t,z)^{2} & \displaystyle \text{lumen section area,}\\ \displaystyle \bar{v}(t,z)=A^{-1}\int _{{\mathcal{S}}(t,z)}v_{z}(t,z)\text{d}S & \displaystyle \text{mean velocity,}\\ \displaystyle s(r/R)\quad \text{such that }v_{z}(t,r,z)=\bar{v}(t,z)s(r/R(t,z)) & \displaystyle \text{velocity profile,}\\ \displaystyle Q(t,z)=\unicode[STIX]{x1D70C}_{f}\int _{{\mathcal{S}}(t,z)}v_{z}\text{d}S=\unicode[STIX]{x1D70C}_{f}A(t,z)\bar{v}(t,z) & \displaystyle \text{flow rate,}\\ \displaystyle P(t,z)=A^{-1}\int _{{\mathcal{S}}(t,z)}p(t,z)\text{d}S & \displaystyle \text{mean pressure.}\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}ll@{}}\displaystyle A(t,z)=|{\mathcal{S}}(t,z)|=\unicode[STIX]{x1D70B}R(t,z)^{2} & \displaystyle \text{lumen section area,}\\ \displaystyle \bar{v}(t,z)=A^{-1}\int _{{\mathcal{S}}(t,z)}v_{z}(t,z)\text{d}S & \displaystyle \text{mean velocity,}\\ \displaystyle s(r/R)\quad \text{such that }v_{z}(t,r,z)=\bar{v}(t,z)s(r/R(t,z)) & \displaystyle \text{velocity profile,}\\ \displaystyle Q(t,z)=\unicode[STIX]{x1D70C}_{f}\int _{{\mathcal{S}}(t,z)}v_{z}\text{d}S=\unicode[STIX]{x1D70C}_{f}A(t,z)\bar{v}(t,z) & \displaystyle \text{flow rate,}\\ \displaystyle P(t,z)=A^{-1}\int _{{\mathcal{S}}(t,z)}p(t,z)\text{d}S & \displaystyle \text{mean pressure.}\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
As for the structure and its interaction with the fluid, we need to introduce a membrane law, which in fact prescribes a relation between the pressure and the lumen area (which is determined by
![]() $d_{r}$
) of the form
$d_{r}$
) of the form
 $$\begin{eqnarray}P(t,z)=P_{\mathit{ext}}+\unicode[STIX]{x1D713}(A(t,z),A_{0}(z),\boldsymbol{\unicode[STIX]{x1D6FD}}(z)),\end{eqnarray}$$
$$\begin{eqnarray}P(t,z)=P_{\mathit{ext}}+\unicode[STIX]{x1D713}(A(t,z),A_{0}(z),\boldsymbol{\unicode[STIX]{x1D6FD}}(z)),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D713}$
is a given function satisfying
$\unicode[STIX]{x1D713}$
is a given function satisfying
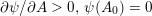 $\unicode[STIX]{x2202}\unicode[STIX]{x1D713}/\unicode[STIX]{x2202}A>0,\,\unicode[STIX]{x1D713}(A_{0})=0$
. Here
$\unicode[STIX]{x2202}\unicode[STIX]{x1D713}/\unicode[STIX]{x2202}A>0,\,\unicode[STIX]{x1D713}(A_{0})=0$
. Here
![]() $\boldsymbol{\unicode[STIX]{x1D6FD}}$
is a vector of parameters describing the mechanical properties of the membrane.
$\boldsymbol{\unicode[STIX]{x1D6FD}}$
is a vector of parameters describing the mechanical properties of the membrane.
By integrating over the sections
![]() ${\mathcal{S}}$
the momentum fluid equation (4.19a
) in the
${\mathcal{S}}$
the momentum fluid equation (4.19a
) in the
![]() $z$
-direction and the mass conservation law (4.19b
), we obtain the system
$z$
-direction and the mass conservation law (4.19b
), we obtain the system
 $$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\boldsymbol{U}}{\unicode[STIX]{x2202}t}+\text{H}(\boldsymbol{U})\frac{\unicode[STIX]{x2202}\boldsymbol{U}}{\unicode[STIX]{x2202}z}+\boldsymbol{B}(\boldsymbol{U})=\mathbf{0}\quad z\in (0,L),\,t>0,\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\boldsymbol{U}}{\unicode[STIX]{x2202}t}+\text{H}(\boldsymbol{U})\frac{\unicode[STIX]{x2202}\boldsymbol{U}}{\unicode[STIX]{x2202}z}+\boldsymbol{B}(\boldsymbol{U})=\mathbf{0}\quad z\in (0,L),\,t>0,\end{eqnarray}$$
where
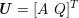 $\boldsymbol{U}=[A\,\,Q]^{T}$
is the vector of the unknowns,
$\boldsymbol{U}=[A\,\,Q]^{T}$
is the vector of the unknowns,
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}=\frac{\int _{S}u_{z}^{2}}{A\bar{v}^{2}}=\frac{1}{A}\int _{0}^{1}s^{2}(y)\text{d}y\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}=\frac{\int _{S}u_{z}^{2}}{A\bar{v}^{2}}=\frac{1}{A}\int _{0}^{1}s^{2}(y)\text{d}y\end{eqnarray}$$
is the Coriolis coefficient,
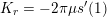 $K_{r}=-2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D707}s^{\prime }(1)$
is the friction parameter,
$K_{r}=-2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D707}s^{\prime }(1)$
is the friction parameter,
 $$\begin{eqnarray}c_{1}=\sqrt{\frac{A}{\unicode[STIX]{x1D70C}_{f}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}A}},\end{eqnarray}$$
$$\begin{eqnarray}c_{1}=\sqrt{\frac{A}{\unicode[STIX]{x1D70C}_{f}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}A}},\end{eqnarray}$$
while
 $$\begin{eqnarray}\displaystyle \text{H}(\boldsymbol{U}) & = & \displaystyle \left[\begin{array}{@{}cc@{}}0 & 1\\ c_{1}^{2}-\unicode[STIX]{x1D6FC}\biggl(\displaystyle \frac{Q}{A}\biggr)^{2} & 2\unicode[STIX]{x1D6FC}\displaystyle \frac{Q}{A}\end{array}\right]\!,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{H}(\boldsymbol{U}) & = & \displaystyle \left[\begin{array}{@{}cc@{}}0 & 1\\ c_{1}^{2}-\unicode[STIX]{x1D6FC}\biggl(\displaystyle \frac{Q}{A}\biggr)^{2} & 2\unicode[STIX]{x1D6FC}\displaystyle \frac{Q}{A}\end{array}\right]\!,\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \boldsymbol{B}(\boldsymbol{U}) & = & \displaystyle \left[\begin{array}{@{}c@{}}0\\ K_{r}\frac{Q}{A}+\displaystyle \frac{A}{\unicode[STIX]{x1D70C}_{f}}\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}A_{0}}\displaystyle \frac{\unicode[STIX]{x2202}A_{0}}{\unicode[STIX]{x2202}z}+\frac{A}{\unicode[STIX]{x1D70C}_{f}}\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}\boldsymbol{\unicode[STIX]{x1D6FD}}}\displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{\unicode[STIX]{x1D6FD}}}{\unicode[STIX]{x2202}z}\end{array}\right]\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{B}(\boldsymbol{U}) & = & \displaystyle \left[\begin{array}{@{}c@{}}0\\ K_{r}\frac{Q}{A}+\displaystyle \frac{A}{\unicode[STIX]{x1D70C}_{f}}\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}A_{0}}\displaystyle \frac{\unicode[STIX]{x2202}A_{0}}{\unicode[STIX]{x2202}z}+\frac{A}{\unicode[STIX]{x1D70C}_{f}}\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}\boldsymbol{\unicode[STIX]{x1D6FD}}}\displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{\unicode[STIX]{x1D6FD}}}{\unicode[STIX]{x2202}z}\end{array}\right]\end{eqnarray}$$
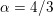 $\unicode[STIX]{x1D6FC}=4/3$
).
$\unicode[STIX]{x1D6FC}=4/3$
).
The term
 $\unicode[STIX]{x2202}A_{0}/\unicode[STIX]{x2202}z$
in
$\unicode[STIX]{x2202}A_{0}/\unicode[STIX]{x2202}z$
in
![]() $\boldsymbol{B}$
is typically non-positive, accounting for vessel ‘tapering’, that is, reduction of the area of the lumen when proceeding from proximal to distal arteries. The term
$\boldsymbol{B}$
is typically non-positive, accounting for vessel ‘tapering’, that is, reduction of the area of the lumen when proceeding from proximal to distal arteries. The term
![]() $\unicode[STIX]{x2202}\boldsymbol{\unicode[STIX]{x1D6FD}}/\unicode[STIX]{x2202}z$
originates from possibly different mechanical properties along the vessel, to describe, for example, the presence of atherosclerotic plaques or vascular prostheses.
$\unicode[STIX]{x2202}\boldsymbol{\unicode[STIX]{x1D6FD}}/\unicode[STIX]{x2202}z$
originates from possibly different mechanical properties along the vessel, to describe, for example, the presence of atherosclerotic plaques or vascular prostheses.
If
![]() $A>0$
, system (4.30) has two real distinct eigenvalues,
$A>0$
, system (4.30) has two real distinct eigenvalues,
 $$\begin{eqnarray}\unicode[STIX]{x1D706}_{1,2}=\unicode[STIX]{x1D6FC}\bar{v}\pm \sqrt{c_{1}^{2}+\bar{v}^{2}\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6FC}-1)}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}_{1,2}=\unicode[STIX]{x1D6FC}\bar{v}\pm \sqrt{c_{1}^{2}+\bar{v}^{2}\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6FC}-1)}\end{eqnarray}$$
(see e.g. Quarteroni and Formaggia Reference Quarteroni and Formaggia2004), so it is strictly hyperbolic (see e.g. LeVeque Reference Leveque1992). Under physiological conditions,
 $c_{1}\gg \unicode[STIX]{x1D6FC}\bar{v}$
, yielding
$c_{1}\gg \unicode[STIX]{x1D6FC}\bar{v}$
, yielding
![]() $\unicode[STIX]{x1D706}_{1}>0$
and
$\unicode[STIX]{x1D706}_{1}>0$
and
![]() $\unicode[STIX]{x1D706}_{2}<0$
, we thus have two waves travelling in opposite directions, associated with corresponding characteristic variables. An explicit expression of these variables as a function of the physical variables could, in general, be derived, that is,
$\unicode[STIX]{x1D706}_{2}<0$
, we thus have two waves travelling in opposite directions, associated with corresponding characteristic variables. An explicit expression of these variables as a function of the physical variables could, in general, be derived, that is,
 $$\begin{eqnarray}W_{i}=\unicode[STIX]{x1D701}_{i}(A,Q),\quad i=1,2.\end{eqnarray}$$
$$\begin{eqnarray}W_{i}=\unicode[STIX]{x1D701}_{i}(A,Q),\quad i=1,2.\end{eqnarray}$$
A simple membrane law (4.29) can be obtained by the algebraic relation
 $$\begin{eqnarray}\unicode[STIX]{x1D713}(A,A_{0},\unicode[STIX]{x1D702})=\unicode[STIX]{x1D702}\frac{\sqrt{A}-\sqrt{A_{0}}}{A_{0}},\quad \text{with }\unicode[STIX]{x1D702}=\frac{\sqrt{\unicode[STIX]{x1D70B}}H_{s}E}{1-\unicode[STIX]{x1D708}^{2}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}(A,A_{0},\unicode[STIX]{x1D702})=\unicode[STIX]{x1D702}\frac{\sqrt{A}-\sqrt{A_{0}}}{A_{0}},\quad \text{with }\unicode[STIX]{x1D702}=\frac{\sqrt{\unicode[STIX]{x1D70B}}H_{s}E}{1-\unicode[STIX]{x1D708}^{2}}\end{eqnarray}$$
(Formaggia, Lamponi and Quarteroni Reference Formaggia, Lamponi and Quarteroni2003, Formaggia et al.
Reference Formaggia, Quarteroni and Vergara2013), where
![]() $\unicode[STIX]{x1D708}$
is the Poisson modulus of the membrane,
$\unicode[STIX]{x1D708}$
is the Poisson modulus of the membrane,
![]() $E$
is its Young’s modulus, and
$E$
is its Young’s modulus, and
![]() $H_{s}$
is its thickness, yielding
$H_{s}$
is its thickness, yielding
 $$\begin{eqnarray}c_{1}=\sqrt{\frac{\unicode[STIX]{x1D702}\sqrt{A}}{2\unicode[STIX]{x1D70C}_{f}A_{0}}}.\end{eqnarray}$$
$$\begin{eqnarray}c_{1}=\sqrt{\frac{\unicode[STIX]{x1D702}\sqrt{A}}{2\unicode[STIX]{x1D70C}_{f}A_{0}}}.\end{eqnarray}$$
This simple law, stating that the membrane radial displacement
![]() $d_{r}$
is linearly proportional to the fluid pressure, has been considered successfully in many applications: see e.g. Steele et al. (Reference Steele, Wan, Ku, Hughes and Taylor2003), Matthys et al. (Reference Matthys, Alastruey, Peiró, Khir, Segers, Verdonck, Parker and Sherwin2007) and Grinberg et al. (Reference Grinberg, Cheever, Anor, Madsen and Karniadakis2010). Other laws have been proposed to account for additional features of arterial walls, such as viscoelasticity, wall-inertia and longitudinal pre-stress (Quarteroni et al.
Reference Quarteroni, Tuveri and Veneziani2000c
, Formaggia et al.
Reference Formaggia, Lamponi and Quarteroni2003).
$d_{r}$
is linearly proportional to the fluid pressure, has been considered successfully in many applications: see e.g. Steele et al. (Reference Steele, Wan, Ku, Hughes and Taylor2003), Matthys et al. (Reference Matthys, Alastruey, Peiró, Khir, Segers, Verdonck, Parker and Sherwin2007) and Grinberg et al. (Reference Grinberg, Cheever, Anor, Madsen and Karniadakis2010). Other laws have been proposed to account for additional features of arterial walls, such as viscoelasticity, wall-inertia and longitudinal pre-stress (Quarteroni et al.
Reference Quarteroni, Tuveri and Veneziani2000c
, Formaggia et al.
Reference Formaggia, Lamponi and Quarteroni2003).
Remark 4.1. One-dimensional models do not allow us to describe secondary flows, such as vortices or recirculation regions. However, they provide average quantities about the axial component of the velocity, the radial vessel wall displacements and the pressure of a complex network at computational costs that are orders of magnitude lower than those of the corresponding three-dimensional FSI models (Kufahl and Clark Reference Kufahl and Clark1985, Hillen, Hoogstraten and Post Reference Hillen, Hoogstraten and Post1986, Blanco et al. Reference Blanco, Watanabe, Passos, Lemos and Feijóo2015, Boileau et al. Reference Boileau, Nithiarasu, Blanco, Muller, Fossan, Hellevik, Donders, Huberts, Willemet and Alastruey2015, Malossi et al. Reference Malossi, Blanco, Crosetto, Deparis and Quarteroni2013).
The accuracy of the solution provided by 1D models is addressed by Avolio (Reference Avolio1980), Steele et al. (Reference Steele, Wan, Ku, Hughes and Taylor2003) and Reymond et al. (Reference Reymond, Merenda, Perren, Rufenacht and Stergiopulos2009), who successfully compare the numerical results of different networks with clinical measurements, and by Matthys et al. (Reference Matthys, Alastruey, Peiró, Khir, Segers, Verdonck, Parker and Sherwin2007) and Muller and Toro (Reference Muller and Toro2013), who perform a comparison with in vitro measurements for a complete network of the cardiovascular system.
A further geometric reduction is represented by the so-called lumped parameter models, which are zero-dimensional (0D) models obtained by integrating the 1D problem over the axial direction. These are typically used to describe the peripheral part of the arterial and venous tree, such as the capillaries and the arterioles.
In this case only dependence on time is allowed, and nominal values of the unknowns are used as representative of the entire compartment. To this end, we introduce the average flow rate and pressure in the district at hand, defined by
 $$\begin{eqnarray}\displaystyle \widehat{Q}(t) & = & \displaystyle \displaystyle \frac{1}{l}\int _{z_{p}}^{z_{d}}Q(t,z)\text{d}z=\displaystyle \frac{\unicode[STIX]{x1D70C}_{f}}{l}\int _{z_{p}}^{z_{d}}\int _{{\mathcal{S}}(t,z)}^{}v_{z}(t,z)\text{d}S\text{d}z,\nonumber\\ \displaystyle \widehat{P}(t) & = & \displaystyle \displaystyle \frac{1}{l}\int _{z_{p}}^{z_{d}}P(t,z)\text{d}z=\displaystyle \frac{1}{V}\int _{z_{p}}^{z_{d}}\int _{{\mathcal{S}}(t,z)}^{}p(t,z)\,\text{d}S\text{d}z\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{Q}(t) & = & \displaystyle \displaystyle \frac{1}{l}\int _{z_{p}}^{z_{d}}Q(t,z)\text{d}z=\displaystyle \frac{\unicode[STIX]{x1D70C}_{f}}{l}\int _{z_{p}}^{z_{d}}\int _{{\mathcal{S}}(t,z)}^{}v_{z}(t,z)\text{d}S\text{d}z,\nonumber\\ \displaystyle \widehat{P}(t) & = & \displaystyle \displaystyle \frac{1}{l}\int _{z_{p}}^{z_{d}}P(t,z)\text{d}z=\displaystyle \frac{1}{V}\int _{z_{p}}^{z_{d}}\int _{{\mathcal{S}}(t,z)}^{}p(t,z)\,\text{d}S\text{d}z\nonumber\end{eqnarray}$$
respectively, where
![]() $z_{p}$
and
$z_{p}$
and
![]() $z_{d}$
are the proximal and longitudinal abscissas of the segment, respectively,
$z_{d}$
are the proximal and longitudinal abscissas of the segment, respectively,
![]() $l$
is its length and
$l$
is its length and
![]() $V$
its volume. The convective term is dropped since in the peripheral sites the velocity is small.
$V$
its volume. The convective term is dropped since in the peripheral sites the velocity is small.
If we take the longitudinal average of the momentum equation given by the first of (4.30) and combine it with (4.34), we obtain the ordinary differential equation (ODE)
 $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D70C}_{f}l}{A_{0}}\displaystyle \frac{\text{d}\widehat{Q}}{\text{d}t}+\displaystyle \frac{\unicode[STIX]{x1D70C}_{f}K_{R}l}{A_{0}^{2}}\widehat{Q}+\widehat{P}_{d}-\widehat{P}_{p}=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D70C}_{f}l}{A_{0}}\displaystyle \frac{\text{d}\widehat{Q}}{\text{d}t}+\displaystyle \frac{\unicode[STIX]{x1D70C}_{f}K_{R}l}{A_{0}^{2}}\widehat{Q}+\widehat{P}_{d}-\widehat{P}_{p}=0,\end{eqnarray}$$
where
![]() $\widehat{P}_{d}$
and
$\widehat{P}_{d}$
and
![]() $\widehat{P}_{p}$
are the distal and proximal pressure, respectively. When taking the longitudinal average of the mass conservation law given by the second of (4.30) and using (4.34), we obtain
$\widehat{P}_{p}$
are the distal and proximal pressure, respectively. When taking the longitudinal average of the mass conservation law given by the second of (4.30) and using (4.34), we obtain
 $$\begin{eqnarray}\displaystyle \frac{\sqrt{A_{0}}l}{\unicode[STIX]{x1D702}}\displaystyle \frac{\text{d}\widehat{P}}{\text{d}t}+\widehat{Q}_{d}-\widehat{Q}_{p}=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\sqrt{A_{0}}l}{\unicode[STIX]{x1D702}}\displaystyle \frac{\text{d}\widehat{P}}{\text{d}t}+\widehat{Q}_{d}-\widehat{Q}_{p}=0,\end{eqnarray}$$
where
![]() $\widehat{Q}_{d}$
and
$\widehat{Q}_{d}$
and
![]() $\widehat{Q}_{p}$
are the distal and proximal flow rate, respectively. See Peiró and Veneziani (Reference Peiró, Veneziani, Quarteroni, Formaggia and Veneziani2009).
$\widehat{Q}_{p}$
are the distal and proximal flow rate, respectively. See Peiró and Veneziani (Reference Peiró, Veneziani, Quarteroni, Formaggia and Veneziani2009).
The two ODEs (4.35, 4.36) can be regarded as the starting point for a 0D description of a compartment model of an arterial tract. In fact, the term
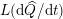 $L(\text{d}\widehat{Q}/\text{d}t)$
, with
$L(\text{d}\widehat{Q}/\text{d}t)$
, with
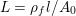 $L=\unicode[STIX]{x1D70C}_{f}l/A_{0}$
, corresponds to the blood acceleration,
$L=\unicode[STIX]{x1D70C}_{f}l/A_{0}$
, corresponds to the blood acceleration,
![]() $R\widehat{Q}$
, with
$R\widehat{Q}$
, with
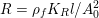 $R=\unicode[STIX]{x1D70C}_{f}K_{R}l/A_{0}^{2}$
, stems from the blood resistance due to the viscosity, while
$R=\unicode[STIX]{x1D70C}_{f}K_{R}l/A_{0}^{2}$
, stems from the blood resistance due to the viscosity, while
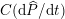 $C(\text{d}\widehat{P}/\text{d}t)$
, with
$C(\text{d}\widehat{P}/\text{d}t)$
, with
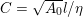 $C=\sqrt{A_{0}}l/\unicode[STIX]{x1D702}$
, is due to the compliance of the vessel wall. Usually an electrical analogy is used to easily interpret 0D models. In particular, the flow rate plays the role of the current whereas the pressure is the potential. Accordingly, the acceleration term is represented by an inductance, the viscosity term by a resistance, and the compliance term by a capacitance.
$C=\sqrt{A_{0}}l/\unicode[STIX]{x1D702}$
, is due to the compliance of the vessel wall. Usually an electrical analogy is used to easily interpret 0D models. In particular, the flow rate plays the role of the current whereas the pressure is the potential. Accordingly, the acceleration term is represented by an inductance, the viscosity term by a resistance, and the compliance term by a capacitance.
To close the system (4.35, 4.36) (featuring four unknowns) we also need to include the boundary conditions originally prescribed on the 1D model. For instance, we can assume a Dirichlet condition at the inlet and a Neumann condition at the outlet. Thus, we may localize the unknown pressure
![]() $\widehat{P}$
at the proximal section (
$\widehat{P}$
at the proximal section (
![]() $\widehat{P}\approx \widehat{P}_{p}$
), assuming that the distal pressure
$\widehat{P}\approx \widehat{P}_{p}$
), assuming that the distal pressure
![]() $\widehat{P}_{d}$
is given. Similarly we assume that the flow rate
$\widehat{P}_{d}$
is given. Similarly we assume that the flow rate
![]() $\widehat{Q}$
is approximated by
$\widehat{Q}$
is approximated by
![]() $\widehat{Q}_{d}$
and that the proximal flow rate
$\widehat{Q}_{d}$
and that the proximal flow rate
![]() $\widehat{Q}_{p}$
is given. Then, from (4.35, 4.36), we obtain
$\widehat{Q}_{p}$
is given. Then, from (4.35, 4.36), we obtain
 $$\begin{eqnarray}\begin{array}{@{}r@{}}\displaystyle \widehat{P}-L\displaystyle \frac{\text{d}\widehat{Q}}{\text{d}t}-R\widehat{Q}=\widehat{P}_{d},\\ \displaystyle C\displaystyle \frac{\text{d}\widehat{P}}{\text{d}t}+\widehat{Q}=\widehat{Q}_{p},\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}r@{}}\displaystyle \widehat{P}-L\displaystyle \frac{\text{d}\widehat{Q}}{\text{d}t}-R\widehat{Q}=\widehat{P}_{d},\\ \displaystyle C\displaystyle \frac{\text{d}\widehat{P}}{\text{d}t}+\widehat{Q}=\widehat{Q}_{p},\end{array}\end{eqnarray}$$
corresponding to the electrical circuit drawn in Figure 4.3. Other sequences corresponding to different boundary conditions and then to different state variables are also possible (see e.g. Quarteroni et al. Reference Quarteroni, Veneziani and Vergara2016c ). Even though these schemes are equivalent in terms of functionality, they play a different role when coupled with higher-dimensional models (see e.g. Quarteroni et al. Reference Quarteroni, Veneziani and Vergara2016c ).

Figure 4.3. Example of lumped parameter scheme for an arterial tract.
For a description of more complex vascular districts, we may combine several 0D elementary tracts, by gluing them via classical continuity arguments. However, the lumped parameter models have mainly been used to provide suitable boundary conditions at the distal artificial sections of 3D and 1D models. In this case, one simple compartment is enough to describe the entire arterial system downstream of the region of interest. Examples are provided by the windkessel model (Westerhof, Lankhaar and Westerhof Reference Westerhof, Lankhaar and Westerhof2009), featuring an average resistance and capacitance, the
![]() $3$
-element windkessel model (Westerhof et al.
Reference Westerhof, Lankhaar and Westerhof2009), where a second resistance is added before the windkessel compartment, and the
$3$
-element windkessel model (Westerhof et al.
Reference Westerhof, Lankhaar and Westerhof2009), where a second resistance is added before the windkessel compartment, and the
![]() $4$
-element windkessel model (Stergiopulos et al.
Reference Stergiopulos, Westerhof, Meister and Westerhof1996, Stergiopulos, Westerhof and Westerhof Reference Stergiopulos, Westerhof and Westerhof1999), where an inductance element is added to the 3-element windkessel model. A 0D model given simply by a resistance is used to provide absorbing boundary conditions at the outlets of the fluid domain in FSI simulations: see e.g. Nobile and Vergara (Reference Nobile and Vergara2008). Instead, more sophisticated approaches account for the propagative dynamics associated with the peripheral circulation, such as the structured tree model (Olufsen et al.
Reference Olufsen, Peskin, Kim, Pedersen, Nadim and Larsen2000), which assumes an asymmetric self-similar structure for the peripheral network.
$4$
-element windkessel model (Stergiopulos et al.
Reference Stergiopulos, Westerhof, Meister and Westerhof1996, Stergiopulos, Westerhof and Westerhof Reference Stergiopulos, Westerhof and Westerhof1999), where an inductance element is added to the 3-element windkessel model. A 0D model given simply by a resistance is used to provide absorbing boundary conditions at the outlets of the fluid domain in FSI simulations: see e.g. Nobile and Vergara (Reference Nobile and Vergara2008). Instead, more sophisticated approaches account for the propagative dynamics associated with the peripheral circulation, such as the structured tree model (Olufsen et al.
Reference Olufsen, Peskin, Kim, Pedersen, Nadim and Larsen2000), which assumes an asymmetric self-similar structure for the peripheral network.
4.5.2 Geometric multiscale coupling
The geometric multiscale approach, first introduced in Quarteroni and Veneziani (Reference Quarteroni, Veneziani and Bristeau1997), consists in the coupling between the 3D, 1D and 0D models. The idea is to use higher-dimensional models in those regions where a very detailed description is required, and lower-dimensional models in the remaining part of the region of interest. This allows us to describe much of the circulatory system.
As discussed earlier, 0D models are typically used to provide boundary conditions for 3D and 1D models. For this reason, the coupling between 3D or 1D models with an extended 0D network has rarely been considered in applications. Instead, the 3D/1D coupling has received a great deal of attention. For this reason, we will detail only the latter case, while referring to Quarteroni, Ragni and Veneziani (Reference Quarteroni, Ragni and Veneziani2001), Quarteroni and Veneziani (Reference Quarteroni and Veneziani2003), Vignon-Clementel et al. (Reference Vignon-Clementel, Figueroa, Jansen and Taylor2006), Kim et al. (Reference Kim, Vignon-Clementel, Figueroa, Ladisa, Jansen, Feinstein and Taylor2009), Migliavacca et al. (Reference Migliavacca, Balossino, Pennati, Dubini, Hsia, de Leval and Bove2006) and Haggerty et al. (Reference Haggerty, Mirabella, Restrepo, de Zélicourt, Rossignac, Sotiropoulos, Spray, Kanter, Fogel, Yoganathan, Holzapfel and Kuhl2013) for the 3D/0D coupling, and Formaggia et al. (Reference Formaggia, Nobile, Quarteroni and Veneziani1999) and Fernández, Milisic and Quarteroni (Reference Fernández, Milisic and Quarteroni2005) for the 1D/0D coupling.
As shown in Figure 4.4, we consider a 3D/FSI problem (4.19) in a 3D cylindrical domain together with initial conditions and boundary conditions at the proximal boundaries and at the external structure.

Figure 4.4. Schematic representation of the reference 3D/1D coupled model.
At the distal boundaries, the 3D problem is coupled with the 1D model (4.30) written in the domain
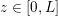 $z\in [0,L]$
, together with initial conditions and a boundary condition at the distal boundary. We let
$z\in [0,L]$
, together with initial conditions and a boundary condition at the distal boundary. We let
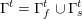 $\unicode[STIX]{x1D6E4}^{t}=\unicode[STIX]{x1D6E4}_{f}^{t}\cup \unicode[STIX]{x1D6E4}_{s}^{t}$
be the coupling interface from the 3D side, which corresponds to the point
$\unicode[STIX]{x1D6E4}^{t}=\unicode[STIX]{x1D6E4}_{f}^{t}\cup \unicode[STIX]{x1D6E4}_{s}^{t}$
be the coupling interface from the 3D side, which corresponds to the point
![]() $z=0$
from the 1D side (see Figure 4.4).
$z=0$
from the 1D side (see Figure 4.4).
A major mathematical issue is how to couple 3D and 1D models at the common interface. Several strategies can be pursued, yielding many (alternative) sets of interface conditions. For a rigorous derivation of the 3D/1D problem and a detailed discussion of the interface conditions, we refer the interested reader to the recent review article by Quarteroni et al. (Reference Quarteroni, Veneziani and Vergara2016c ).
Here we will follow the guiding principle described in Formaggia et al. (Reference Formaggia, Quarteroni and Vergara2013), where suitable interface conditions are derived from a global energy estimate. In particular, we introduce, together with the 3D energy (4.21), the 1D energy
 $$\begin{eqnarray}{\mathcal{E}}_{1D}(t)=\displaystyle \frac{\unicode[STIX]{x1D70C}_{f}}{2}\int _{0}^{L}A\,\bar{v}^{2}\text{d}x+\int _{0}^{L}\unicode[STIX]{x1D712}(A)\text{d}x\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{E}}_{1D}(t)=\displaystyle \frac{\unicode[STIX]{x1D70C}_{f}}{2}\int _{0}^{L}A\,\bar{v}^{2}\text{d}x+\int _{0}^{L}\unicode[STIX]{x1D712}(A)\text{d}x\end{eqnarray}$$
(Formaggia et al.
Reference Formaggia, Gerbeau, Nobile and Quarteroni2001), where
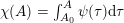 $\unicode[STIX]{x1D712}(A)=\int _{A_{0}}^{A}\unicode[STIX]{x1D713}(\unicode[STIX]{x1D70F})\text{d}\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D712}(A)=\int _{A_{0}}^{A}\unicode[STIX]{x1D713}(\unicode[STIX]{x1D70F})\text{d}\unicode[STIX]{x1D70F}$
and
![]() $\unicode[STIX]{x1D713}$
is the vessel law (see (4.29)). Note that the stand-alone 1D problem satisfies bounds for this energy functional as proved in Formaggia et al. (Reference Formaggia, Gerbeau, Nobile and Quarteroni2001).
$\unicode[STIX]{x1D713}$
is the vessel law (see (4.29)). Note that the stand-alone 1D problem satisfies bounds for this energy functional as proved in Formaggia et al. (Reference Formaggia, Gerbeau, Nobile and Quarteroni2001).
Let
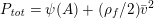 $P_{\mathit{tot}}=\unicode[STIX]{x1D713}(A)+(\unicode[STIX]{x1D70C}_{f}/2)\bar{v}^{2}$
be the total pressure for the 1D model, and let
$P_{\mathit{tot}}=\unicode[STIX]{x1D713}(A)+(\unicode[STIX]{x1D70C}_{f}/2)\bar{v}^{2}$
be the total pressure for the 1D model, and let
 $p_{\mathit{tot}}=p+(\unicode[STIX]{x1D70C}_{f}/2)|\boldsymbol{v}|^{2}$
be that of the 3D model. For the interface coupling conditions holding at
$p_{\mathit{tot}}=p+(\unicode[STIX]{x1D70C}_{f}/2)|\boldsymbol{v}|^{2}$
be that of the 3D model. For the interface coupling conditions holding at
![]() $\unicode[STIX]{x1D6E4}^{t}$
, let us assume that the following inequality holds:
$\unicode[STIX]{x1D6E4}^{t}$
, let us assume that the following inequality holds:
 $$\begin{eqnarray}\int _{\unicode[STIX]{x1D6E4}_{f}^{t}}\boldsymbol{T}_{f}(\boldsymbol{v},p_{\mathit{tot}})\boldsymbol{n}\cdot \boldsymbol{v}\text{d}\unicode[STIX]{x1D6FE}+\int _{\unicode[STIX]{x1D6E4}_{s}^{t}}\boldsymbol{T}_{s}(\boldsymbol{d})\boldsymbol{n}\cdot \dot{\boldsymbol{d}}\text{d}\unicode[STIX]{x1D6FE}+Q|_{z=0}\,P_{\mathit{tot}}|_{z=0}\leq 0.\end{eqnarray}$$
$$\begin{eqnarray}\int _{\unicode[STIX]{x1D6E4}_{f}^{t}}\boldsymbol{T}_{f}(\boldsymbol{v},p_{\mathit{tot}})\boldsymbol{n}\cdot \boldsymbol{v}\text{d}\unicode[STIX]{x1D6FE}+\int _{\unicode[STIX]{x1D6E4}_{s}^{t}}\boldsymbol{T}_{s}(\boldsymbol{d})\boldsymbol{n}\cdot \dot{\boldsymbol{d}}\text{d}\unicode[STIX]{x1D6FE}+Q|_{z=0}\,P_{\mathit{tot}}|_{z=0}\leq 0.\end{eqnarray}$$
Then, for all
![]() $t>0$
, the coupled 3D/1D problem (4.19, 4.30) with homogeneous boundary conditions satisfies the energy decay property
$t>0$
, the coupled 3D/1D problem (4.19, 4.30) with homogeneous boundary conditions satisfies the energy decay property
 $$\begin{eqnarray}\displaystyle \frac{\text{d}}{\text{d}t}({\mathcal{E}}^{3D}(t)+{\mathcal{E}}^{1D}(t))\leq 0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\text{d}}{\text{d}t}({\mathcal{E}}^{3D}(t)+{\mathcal{E}}^{1D}(t))\leq 0.\end{eqnarray}$$
For the proof see Formaggia et al. (Reference Formaggia, Quarteroni and Vergara2013).
The above result provides an indication of how to find suitable interface conditions for the 3D/1D coupled problem. In particular, for inequality (4.38) to be fulfilled it is sufficient that the interface conditions
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}_{f}\int _{\unicode[STIX]{x1D6E4}_{f}^{t}}\boldsymbol{v}\cdot \boldsymbol{n}\text{d}\unicode[STIX]{x1D6FE} & = & \displaystyle Q|_{z=0},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}_{f}\int _{\unicode[STIX]{x1D6E4}_{f}^{t}}\boldsymbol{v}\cdot \boldsymbol{n}\text{d}\unicode[STIX]{x1D6FE} & = & \displaystyle Q|_{z=0},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle (\boldsymbol{T}_{f}(\boldsymbol{v},p_{\mathit{tot}})\boldsymbol{n})|_{\unicode[STIX]{x1D6E4}_{f}^{t}} & = & \displaystyle -P_{\mathit{tot}}|_{z=0}\boldsymbol{n}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\boldsymbol{T}_{f}(\boldsymbol{v},p_{\mathit{tot}})\boldsymbol{n})|_{\unicode[STIX]{x1D6E4}_{f}^{t}} & = & \displaystyle -P_{\mathit{tot}}|_{z=0}\boldsymbol{n}\end{eqnarray}$$
 $$\begin{eqnarray}\boldsymbol{T}_{s}(\boldsymbol{d})\boldsymbol{n}=\pmb{{\it 0}}\quad \text{on }\unicode[STIX]{x1D6E4}_{s}^{t}\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{T}_{s}(\boldsymbol{d})\boldsymbol{n}=\pmb{{\it 0}}\quad \text{on }\unicode[STIX]{x1D6E4}_{s}^{t}\end{eqnarray}$$
for the structure (Formaggia, Moura and Nobile Reference Formaggia, Moura and Nobile2007, Formaggia et al. Reference Formaggia, Quarteroni and Vergara2013). Similarly, inequality (4.38) holds if relation (4.40) is replaced by
 $$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{d}\cdot \boldsymbol{n}=\pmb{{\it 0}} & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6E4}_{s}^{t},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{d}\cdot \boldsymbol{n}=\pmb{{\it 0}} & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6E4}_{s}^{t},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle (\boldsymbol{T}_{s}(\boldsymbol{d})\boldsymbol{n})\times \boldsymbol{n}=\pmb{{\it 0}} & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6E4}_{s}^{t}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle (\boldsymbol{T}_{s}(\boldsymbol{d})\boldsymbol{n})\times \boldsymbol{n}=\pmb{{\it 0}} & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6E4}_{s}^{t}.\end{eqnarray}$$
Usually, dynamic interface conditions involving the pressure (instead of the total pressure) are considered in place of (4.39b ), such as
 $$\begin{eqnarray}\frac{1}{|\unicode[STIX]{x1D6E4}_{f}^{t}|}\int _{\unicode[STIX]{x1D6E4}_{f}^{t}}\boldsymbol{T}_{f}(\boldsymbol{v},p)\boldsymbol{n}\text{d}\unicode[STIX]{x1D6FE}=-\unicode[STIX]{x1D713}(A|_{z=0})\boldsymbol{n}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{|\unicode[STIX]{x1D6E4}_{f}^{t}|}\int _{\unicode[STIX]{x1D6E4}_{f}^{t}}\boldsymbol{T}_{f}(\boldsymbol{v},p)\boldsymbol{n}\text{d}\unicode[STIX]{x1D6FE}=-\unicode[STIX]{x1D713}(A|_{z=0})\boldsymbol{n}.\end{eqnarray}$$
However, the above condition does not satisfy the compatibility condition (4.38). More precisely, in this case we have
 $$\begin{eqnarray}\displaystyle \frac{\text{d}}{\text{d}t}({\mathcal{E}}^{3D}(t)+{\mathcal{E}}^{1D}(t))=\displaystyle \frac{\unicode[STIX]{x1D70C}_{f}}{2}\biggl(\frac{(Q(t)|_{z=0})^{3}}{(A(t)|_{z=0})^{2}}-\int _{\unicode[STIX]{x1D6E4}_{f}^{t}}|\boldsymbol{v}(t)|^{2}\boldsymbol{v}(t)\cdot \boldsymbol{n}\text{d}\unicode[STIX]{x1D6FE}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\text{d}}{\text{d}t}({\mathcal{E}}^{3D}(t)+{\mathcal{E}}^{1D}(t))=\displaystyle \frac{\unicode[STIX]{x1D70C}_{f}}{2}\biggl(\frac{(Q(t)|_{z=0})^{3}}{(A(t)|_{z=0})^{2}}-\int _{\unicode[STIX]{x1D6E4}_{f}^{t}}|\boldsymbol{v}(t)|^{2}\boldsymbol{v}(t)\cdot \boldsymbol{n}\text{d}\unicode[STIX]{x1D6FE}\biggr).\end{eqnarray}$$
Even though the right-hand side is not necessarily (always) negative, numerical evidence indicates that condition (4.42) leads to stable results for haemodynamic applications: see Malossi et al. (Reference Malossi, Blanco, Crosetto, Deparis and Quarteroni2013). This interface condition is indeed the most commonly used among dynamic ones.
4.6 Numerical strategies
In this section we comment on the numerical solution of the problems presented in the previous subsections. Because of the complexity of the problem, we do not seek to be exhaustive. Instead, we review some of most suitable methods for haemodynamics. In particular, for space discretization, we will focus on Galerkin-type methods, such as finite elements, spectral elements and discontinuous Galerkin methods.
We will use the following notation. Let
![]() $\unicode[STIX]{x1D6E5}t$
and
$\unicode[STIX]{x1D6E5}t$
and
![]() $h$
be the time and space discretization parameters. In our examples
$h$
be the time and space discretization parameters. In our examples
![]() $\unicode[STIX]{x1D6E5}t$
is assumed to be fixed, but adaptive strategies could be considered as well: see e.g. Veneziani and Villa (Reference Veneziani and Villa2013). Correspondingly, the discrete times are
$\unicode[STIX]{x1D6E5}t$
is assumed to be fixed, but adaptive strategies could be considered as well: see e.g. Veneziani and Villa (Reference Veneziani and Villa2013). Correspondingly, the discrete times are
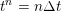 $t^{n}=n\unicode[STIX]{x1D6E5}t$
. As usual,
$t^{n}=n\unicode[STIX]{x1D6E5}t$
. As usual,
![]() $h$
is instead defined as a representative value of the mesh size, for example
$h$
is instead defined as a representative value of the mesh size, for example
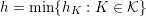 $h=\min \{h_{K}:K\in {\mathcal{K}}\}$
, where
$h=\min \{h_{K}:K\in {\mathcal{K}}\}$
, where
![]() ${\mathcal{K}}$
is the set of all tetrahedra in the mesh and
${\mathcal{K}}$
is the set of all tetrahedra in the mesh and
![]() $h_{K}$
is the radius of the sphere inscribed in
$h_{K}$
is the radius of the sphere inscribed in
![]() $K\in {\mathcal{K}}$
. Given the functions
$K\in {\mathcal{K}}$
. Given the functions
![]() $w(t)$
and
$w(t)$
and
![]() $z(\boldsymbol{x})$
, we let
$z(\boldsymbol{x})$
, we let
![]() $w^{n}$
denote the approximation of
$w^{n}$
denote the approximation of
![]() $w(t^{n})$
and let
$w(t^{n})$
and let
![]() $z_{h}(\boldsymbol{x})$
be the Galerkin approximation of
$z_{h}(\boldsymbol{x})$
be the Galerkin approximation of
![]() $z(\boldsymbol{x})$
.
$z(\boldsymbol{x})$
.
4.6.1 Numerical methods for the fluid problem
We start by reviewing some numerical methods for the fluid problem (4.1) together with its initial and boundary conditions.
As for the time discretization, we usually consider implicit methods with a semi-implicit treatment of the convective term and (for a moving domain) of the fluid domain. The problem is solved at discrete time
![]() $t^{n+1}$
in the domain
$t^{n+1}$
in the domain
![]() $\unicode[STIX]{x1D6FA}_{f}^{\ast }$
and with convective term
$\unicode[STIX]{x1D6FA}_{f}^{\ast }$
and with convective term
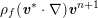 $\unicode[STIX]{x1D70C}_{f}(\boldsymbol{v}^{\ast }\cdot \unicode[STIX]{x1D6FB})\boldsymbol{v}^{n+1}$
, where
$\unicode[STIX]{x1D70C}_{f}(\boldsymbol{v}^{\ast }\cdot \unicode[STIX]{x1D6FB})\boldsymbol{v}^{n+1}$
, where
![]() $\unicode[STIX]{x1D6FA}_{f}^{\ast }$
and
$\unicode[STIX]{x1D6FA}_{f}^{\ast }$
and
![]() $\boldsymbol{v}^{\ast }$
are suitable extrapolations of
$\boldsymbol{v}^{\ast }$
are suitable extrapolations of
![]() $\unicode[STIX]{x1D6FA}_{f}^{n+1}$
and
$\unicode[STIX]{x1D6FA}_{f}^{n+1}$
and
![]() $\boldsymbol{v}^{n+1}$
of the same order as the time discretization. This choice introduces a CFL-like (Courant–Friedrichs–Lewy) restriction on the time step to preserve absolute stability (Quarteroni and Valli Reference Quarteroni and Valli1994). However, this condition is very mild in haemodynamic applications, since, for accuracy purposes, the pulsatility of the blood signal and the quick dynamics around systole can only be accommodated by choosing a small
$\boldsymbol{v}^{n+1}$
of the same order as the time discretization. This choice introduces a CFL-like (Courant–Friedrichs–Lewy) restriction on the time step to preserve absolute stability (Quarteroni and Valli Reference Quarteroni and Valli1994). However, this condition is very mild in haemodynamic applications, since, for accuracy purposes, the pulsatility of the blood signal and the quick dynamics around systole can only be accommodated by choosing a small
![]() $\unicode[STIX]{x1D6E5}t$
. Usually, a second-order approximation is considered a good choice in haemodynamics; in this respect, the second-order backward difference formula (BDF2) and Crank–Nicolson are the most widely used methods (Quarteroni, Sacco and Saleri Reference Quarteroni, Sacco and Saleri2000a
).
$\unicode[STIX]{x1D6E5}t$
. Usually, a second-order approximation is considered a good choice in haemodynamics; in this respect, the second-order backward difference formula (BDF2) and Crank–Nicolson are the most widely used methods (Quarteroni, Sacco and Saleri Reference Quarteroni, Sacco and Saleri2000a
).
The first class of methods we present is based on a decomposition of the semi-discrete problem at the spatial continuous level (differential splitting or projection methods). The basic idea underlying these methods is to split the computation of velocity and pressure, with a final step aiming to recover the incompressibility constraint. In what follows we detail the Chorin–Teman method (Chorin Reference Chorin1968, Temam Reference Temam1969), originally proposed for homogeneous Dirichlet conditions and fixed domain, which is the progenitor of these methods. We only detail the case of the backward Euler discretization.
Chorin–Temam method
For
![]() $n\geq 0$
, at time
$n\geq 0$
, at time
![]() $t^{n+1}$
:
$t^{n+1}$
:
-
(1) Solve in
 $\unicode[STIX]{x1D6FA}_{f}$
the advection-reaction-diffusion problem with homogeneous Dirichlet condition for the intermediate unknown velocity
$\unicode[STIX]{x1D6FA}_{f}$
the advection-reaction-diffusion problem with homogeneous Dirichlet condition for the intermediate unknown velocity
 $\widetilde{\boldsymbol{v}}^{n+1}$
:
$\widetilde{\boldsymbol{v}}^{n+1}$
:  $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{f}\frac{\widetilde{\boldsymbol{v}}^{n+1}-\boldsymbol{v}^{n}}{\unicode[STIX]{x1D6E5}t}-\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FB}\widetilde{\boldsymbol{v}}^{n+1}+(\unicode[STIX]{x1D6FB}\widetilde{\boldsymbol{v}}^{n+1})^{T})+\unicode[STIX]{x1D70C}_{f}(\boldsymbol{v}^{n}\cdot \unicode[STIX]{x1D6FB})\widetilde{\boldsymbol{v}}^{n+1}=\mathbf{0}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{f}\frac{\widetilde{\boldsymbol{v}}^{n+1}-\boldsymbol{v}^{n}}{\unicode[STIX]{x1D6E5}t}-\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FB}\widetilde{\boldsymbol{v}}^{n+1}+(\unicode[STIX]{x1D6FB}\widetilde{\boldsymbol{v}}^{n+1})^{T})+\unicode[STIX]{x1D70C}_{f}(\boldsymbol{v}^{n}\cdot \unicode[STIX]{x1D6FB})\widetilde{\boldsymbol{v}}^{n+1}=\mathbf{0}.\end{eqnarray}$$
-
(2) Solve in
 $\unicode[STIX]{x1D6FA}_{f}$
the pressure problem with homogeneous Neumann conditions:
$\unicode[STIX]{x1D6FA}_{f}$
the pressure problem with homogeneous Neumann conditions:  $$\begin{eqnarray}\triangle p^{n+1}=\frac{\unicode[STIX]{x1D70C}_{f}}{\unicode[STIX]{x1D6E5}t}\unicode[STIX]{x1D6FB}\cdot \widetilde{\boldsymbol{v}}^{n+1}.\end{eqnarray}$$
$$\begin{eqnarray}\triangle p^{n+1}=\frac{\unicode[STIX]{x1D70C}_{f}}{\unicode[STIX]{x1D6E5}t}\unicode[STIX]{x1D6FB}\cdot \widetilde{\boldsymbol{v}}^{n+1}.\end{eqnarray}$$
-
(3) Correct the velocity:
 $$\begin{eqnarray}\boldsymbol{v}^{n+1}=\widetilde{\boldsymbol{v}}^{n+1}-\frac{\unicode[STIX]{x1D6E5}t}{\unicode[STIX]{x1D70C}_{f}}\unicode[STIX]{x1D6FB}p^{n+1}.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{v}^{n+1}=\widetilde{\boldsymbol{v}}^{n+1}-\frac{\unicode[STIX]{x1D6E5}t}{\unicode[STIX]{x1D70C}_{f}}\unicode[STIX]{x1D6FB}p^{n+1}.\end{eqnarray}$$
This splitting method is based on the Ladyzhenskaya theorem (Girault and Raviart Reference Girault and Raviart1986), which states that a vector function belonging to
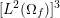 $[L^{2}(\unicode[STIX]{x1D6FA}_{f})]^{3}$
can always be decomposed as the sum of a solenoidal part and a gradient term. In fact, the correction step corresponds to projecting the intermediate velocity onto
$[L^{2}(\unicode[STIX]{x1D6FA}_{f})]^{3}$
can always be decomposed as the sum of a solenoidal part and a gradient term. In fact, the correction step corresponds to projecting the intermediate velocity onto
 $$\begin{eqnarray}\boldsymbol{H}=\{\boldsymbol{w}\in [L^{2}(\unicode[STIX]{x1D6FA}_{f})]^{3}:\,\unicode[STIX]{x1D6FB}\cdot \boldsymbol{w}=0,\,\boldsymbol{w}\cdot \boldsymbol{n}|_{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}_{f}}=0\}.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{H}=\{\boldsymbol{w}\in [L^{2}(\unicode[STIX]{x1D6FA}_{f})]^{3}:\,\unicode[STIX]{x1D6FB}\cdot \boldsymbol{w}=0,\,\boldsymbol{w}\cdot \boldsymbol{n}|_{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}_{f}}=0\}.\end{eqnarray}$$
Thus, it is possible to show that
![]() $\boldsymbol{v}^{n+1}$
and
$\boldsymbol{v}^{n+1}$
and
![]() $p^{n+1}$
are in fact solutions of the original semi-discrete problem. The Chorin–Temam method is very effective since it overcomes the saddle-point nature of the problem and solves two standard uncoupled elliptic problems. However, it suffers from inaccuracies at the boundary. In particular, the tangential velocity cannot be controlled (see the definition of
$p^{n+1}$
are in fact solutions of the original semi-discrete problem. The Chorin–Temam method is very effective since it overcomes the saddle-point nature of the problem and solves two standard uncoupled elliptic problems. However, it suffers from inaccuracies at the boundary. In particular, the tangential velocity cannot be controlled (see the definition of
![]() $\boldsymbol{H}$
) and spurious pressure values appear as a consequence of the artificial Neumann condition for the pressure problem (Rannacher Reference Rannacher1992). This has an effect on the accuracy of the semi-discrete solution. In particular, the following error estimate holds true (Rannacher Reference Rannacher1992):
$\boldsymbol{H}$
) and spurious pressure values appear as a consequence of the artificial Neumann condition for the pressure problem (Rannacher Reference Rannacher1992). This has an effect on the accuracy of the semi-discrete solution. In particular, the following error estimate holds true (Rannacher Reference Rannacher1992):
 $$\begin{eqnarray}\Vert \boldsymbol{v}(t^{n},\boldsymbol{x})-\boldsymbol{v}^{n}(\boldsymbol{x})\Vert _{[H^{1}]^{3}}+\Vert p(t^{n},\boldsymbol{x})-p^{n}(\boldsymbol{x})\Vert _{L^{2}}\lesssim \sqrt{\unicode[STIX]{x1D6E5}t}.\end{eqnarray}$$
$$\begin{eqnarray}\Vert \boldsymbol{v}(t^{n},\boldsymbol{x})-\boldsymbol{v}^{n}(\boldsymbol{x})\Vert _{[H^{1}]^{3}}+\Vert p(t^{n},\boldsymbol{x})-p^{n}(\boldsymbol{x})\Vert _{L^{2}}\lesssim \sqrt{\unicode[STIX]{x1D6E5}t}.\end{eqnarray}$$
The use of higher-order time approximations leads to the same accuracy.
An improvement of the above method is given by the rotational incremental variant of the Chorin–Temam scheme (Timmermans, Minev and van de Vosse Reference Timmermans, Minev and van de Vosse1996). Below we detail the case of BDF2 and second-order extrapolation of the convective term, since the first-order approximation does not lead to any improvement.
Rotational–incremental Chorin–Temam method
For
![]() $n\geq 0$
, at time
$n\geq 0$
, at time
![]() $t^{n+1}$
:
$t^{n+1}$
:
-
(1) Solve in
 $\unicode[STIX]{x1D6FA}_{f}$
the advection-reaction-diffusion problem with homogeneous Dirichlet condition in the intermediate unknown velocity
$\unicode[STIX]{x1D6FA}_{f}$
the advection-reaction-diffusion problem with homogeneous Dirichlet condition in the intermediate unknown velocity
 $\widetilde{\boldsymbol{v}}^{n+1}$
:
$\widetilde{\boldsymbol{v}}^{n+1}$
:  $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D70C}_{f}\frac{3\widetilde{\boldsymbol{v}}^{n+1}-4\boldsymbol{v}^{n}+\boldsymbol{v}^{n-1}}{2\unicode[STIX]{x1D6E5}t}-\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FB}\widetilde{\boldsymbol{v}}^{n+1}+(\unicode[STIX]{x1D6FB}\widetilde{\boldsymbol{v}}^{n+1})^{T})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D70C}_{f}((2\boldsymbol{v}^{n}-\boldsymbol{v}^{n-1})\cdot \unicode[STIX]{x1D6FB})\widetilde{\boldsymbol{v}}^{n+1}+\unicode[STIX]{x1D6FB}p^{n}=\mathbf{0}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D70C}_{f}\frac{3\widetilde{\boldsymbol{v}}^{n+1}-4\boldsymbol{v}^{n}+\boldsymbol{v}^{n-1}}{2\unicode[STIX]{x1D6E5}t}-\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FB}\widetilde{\boldsymbol{v}}^{n+1}+(\unicode[STIX]{x1D6FB}\widetilde{\boldsymbol{v}}^{n+1})^{T})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D70C}_{f}((2\boldsymbol{v}^{n}-\boldsymbol{v}^{n-1})\cdot \unicode[STIX]{x1D6FB})\widetilde{\boldsymbol{v}}^{n+1}+\unicode[STIX]{x1D6FB}p^{n}=\mathbf{0}.\nonumber\end{eqnarray}$$
-
(2) Solve the pressure problem:
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}ll@{}}\displaystyle \triangle p^{n+1}=\triangle p^{n}+\biggl(\frac{3\unicode[STIX]{x1D70C}_{f}}{2\unicode[STIX]{x1D6E5}t}-\unicode[STIX]{x1D707}\biggr)\unicode[STIX]{x1D6FB}\cdot \widetilde{\boldsymbol{v}}^{n+1}, & \displaystyle \boldsymbol{x}\in \unicode[STIX]{x1D6FA}_{f},\\ \displaystyle \frac{\unicode[STIX]{x2202}p^{n+1}}{\unicode[STIX]{x2202}\boldsymbol{n}}=\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FB}\times \unicode[STIX]{x1D6FB}\times \widetilde{\boldsymbol{v}}^{n+1})\cdot \boldsymbol{n}, & \displaystyle \boldsymbol{x}\in \unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}_{f}.\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}ll@{}}\displaystyle \triangle p^{n+1}=\triangle p^{n}+\biggl(\frac{3\unicode[STIX]{x1D70C}_{f}}{2\unicode[STIX]{x1D6E5}t}-\unicode[STIX]{x1D707}\biggr)\unicode[STIX]{x1D6FB}\cdot \widetilde{\boldsymbol{v}}^{n+1}, & \displaystyle \boldsymbol{x}\in \unicode[STIX]{x1D6FA}_{f},\\ \displaystyle \frac{\unicode[STIX]{x2202}p^{n+1}}{\unicode[STIX]{x2202}\boldsymbol{n}}=\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FB}\times \unicode[STIX]{x1D6FB}\times \widetilde{\boldsymbol{v}}^{n+1})\cdot \boldsymbol{n}, & \displaystyle \boldsymbol{x}\in \unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}_{f}.\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
-
(3) Correct the velocity:
 $$\begin{eqnarray}\boldsymbol{v}^{n+1}=\widetilde{\boldsymbol{v}}^{n+1}-\frac{2}{3}\frac{\unicode[STIX]{x1D6E5}t}{\unicode[STIX]{x1D70C}_{f}}\unicode[STIX]{x1D6FB}(p^{n+1}-p^{n}+\unicode[STIX]{x1D707}\unicode[STIX]{x1D6FB}\cdot \widetilde{\boldsymbol{v}}^{n+1}).\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{v}^{n+1}=\widetilde{\boldsymbol{v}}^{n+1}-\frac{2}{3}\frac{\unicode[STIX]{x1D6E5}t}{\unicode[STIX]{x1D70C}_{f}}\unicode[STIX]{x1D6FB}(p^{n+1}-p^{n}+\unicode[STIX]{x1D707}\unicode[STIX]{x1D6FB}\cdot \widetilde{\boldsymbol{v}}^{n+1}).\end{eqnarray}$$
Unlike the classical Chorin–Temam scheme, in the above method the boundary conditions for the pressure problem are consistent, and no numerical boundary layer for the pressure is observed. This is confirmed by the improved error estimate
 $$\begin{eqnarray}\Vert \boldsymbol{v}(t^{n},\boldsymbol{x})-\boldsymbol{v}^{n}(\boldsymbol{x})\Vert _{[H^{1}]^{3}}+\Vert p(t^{n},\boldsymbol{x})-p^{n}(\boldsymbol{x})\Vert _{L^{2}}\lesssim \unicode[STIX]{x1D6E5}t^{3/2}\end{eqnarray}$$
$$\begin{eqnarray}\Vert \boldsymbol{v}(t^{n},\boldsymbol{x})-\boldsymbol{v}^{n}(\boldsymbol{x})\Vert _{[H^{1}]^{3}}+\Vert p(t^{n},\boldsymbol{x})-p^{n}(\boldsymbol{x})\Vert _{L^{2}}\lesssim \unicode[STIX]{x1D6E5}t^{3/2}\end{eqnarray}$$
(Guermond and Shen Reference Guermond and Shen2006).
The above two methods belong to the general class of pressure-correction methods; see also Codina and Badia (Reference Codina and Badia2006), Guermond, Minev and Shen (Reference Guermond, Minev and Shen2006) and Guermond and Quartapelle (Reference Guermond and Quartapelle1998), for example. A different class is obtained by switching the role of velocity and pressure in the splitting, that is, the viscous term is now ignored or treated explicitly in the first step and the velocity is then corrected accordingly (velocity-correction schemes: Orszag, Israeli and Deville Reference Orszag, Israeli and Deville1986, Karniadakis, Israeli and Orszag Reference Karniadakis, Israeli and Orszag1991). These schemes are characterized by the same non-optimal error estimates as the pressure-correction schemes due to artificial Neumann conditions for the pressure problem. Again, an improvement could be obtained by considering a rotational-incremental variant (Guermond and Shen Reference Guermond and Shen2003).
In haemodynamics it is often the case that Neumann boundary conditions are prescribed at some artificial section. The extension of the differential splitting methods to this case is addressed in Guermond, Minev and Shen (Reference Guermond, Minev and Shen2005): on the Neumann boundary we have an artificial Dirichlet condition for the pressure, which again diminishes the optimal rate of convergence with respect to
![]() $\unicode[STIX]{x1D6E5}t$
.
$\unicode[STIX]{x1D6E5}t$
.
Given the next methods we are going to review, it is convenient to introduce the algebraic problem arising from the application of a Galerkin-like method to the semi-discrete-in-time problem. First of all we notice that the solvability of the discretized-in-space problem is guaranteed by a suitable compatible choice of the approximation spaces for the velocity and the pressure in order to satisfy the discrete inf-sup stability condition (Quarteroni and Valli Reference Quarteroni and Valli1994). As is well known, an example of finite elements for a tetrahedral mesh is provided by piecewise polynomials of order 2 for the velocity approximation and of order 1 for the pressure approximation. This choice guarantees the existence and uniqueness of the solution to the linearized fully discrete problem and is often used to provide a stable solution in haemodynamics. In this case, we have the optimal error estimate
 $$\begin{eqnarray}\Vert \boldsymbol{v}^{n}(\boldsymbol{x})-\boldsymbol{v}_{h}^{n}(\boldsymbol{x})\Vert _{[H^{1}]^{3}}+\Vert p^{n}(\boldsymbol{x})-p_{h}^{n}(\boldsymbol{x})\Vert _{L^{2}}\lesssim h^{2},\end{eqnarray}$$
$$\begin{eqnarray}\Vert \boldsymbol{v}^{n}(\boldsymbol{x})-\boldsymbol{v}_{h}^{n}(\boldsymbol{x})\Vert _{[H^{1}]^{3}}+\Vert p^{n}(\boldsymbol{x})-p_{h}^{n}(\boldsymbol{x})\Vert _{L^{2}}\lesssim h^{2},\end{eqnarray}$$
provided that
![]() $\boldsymbol{v}^{n}$
and
$\boldsymbol{v}^{n}$
and
![]() $p^{n}$
are sufficiently regular. (For other stable choices see Quarteroni and Valli Reference Quarteroni and Valli1994 and Boffi, Brezzi and Fortin Reference Boffi, Brezzi and Fortin2013.) Alternatively, suitable stabilization terms could be added to the problem, circumventing the inf-sup condition and allowing the use of polynomials of equal order. In this case, additional terms are added to the mass conservation equation and, if needed, to the momentum conservation equation. Usually, these techniques also stabilize convected-dominated problems arising when the Reynolds number is high, for example in the aorta or in stenotic carotid arteries. One technique is streamline upwind/Petrov–Galerkin (SUPG) (Muller et al.
Reference Muller, Sahni, Lia, Jansen, Shephard and Taylor2005). A generalization of SUPG is the variational multiscale (VMS) method (Hughes Reference Hughes1995, Hughes, Mazzei and Jansen Reference Hughes, Mazzei and Jansen2000), which is based on decomposition of the unknown into two terms, one accounting for the large scales and the other for the small scales. The same decomposition is used for the test functions, so that a system of two coupled problems is obtained. The VMS method is also useful since it allows modelling of transition to turbulence effects, which may occur in some pathological conditions such as stenoses (Akkerman et al.
Reference Akkerman, Bazilevs, Calo, Hughes and Hulshoff2008). For an application to haemodynamics, see Forti and Dede’ (Reference Forti and Dede’2015).
$p^{n}$
are sufficiently regular. (For other stable choices see Quarteroni and Valli Reference Quarteroni and Valli1994 and Boffi, Brezzi and Fortin Reference Boffi, Brezzi and Fortin2013.) Alternatively, suitable stabilization terms could be added to the problem, circumventing the inf-sup condition and allowing the use of polynomials of equal order. In this case, additional terms are added to the mass conservation equation and, if needed, to the momentum conservation equation. Usually, these techniques also stabilize convected-dominated problems arising when the Reynolds number is high, for example in the aorta or in stenotic carotid arteries. One technique is streamline upwind/Petrov–Galerkin (SUPG) (Muller et al.
Reference Muller, Sahni, Lia, Jansen, Shephard and Taylor2005). A generalization of SUPG is the variational multiscale (VMS) method (Hughes Reference Hughes1995, Hughes, Mazzei and Jansen Reference Hughes, Mazzei and Jansen2000), which is based on decomposition of the unknown into two terms, one accounting for the large scales and the other for the small scales. The same decomposition is used for the test functions, so that a system of two coupled problems is obtained. The VMS method is also useful since it allows modelling of transition to turbulence effects, which may occur in some pathological conditions such as stenoses (Akkerman et al.
Reference Akkerman, Bazilevs, Calo, Hughes and Hulshoff2008). For an application to haemodynamics, see Forti and Dede’ (Reference Forti and Dede’2015).
Here we introduce the algebraic problem related to the fully discretized linearized problem. For the sake of exposition, we limit ourselves to the cases without stabilization terms. For the more general case, we refer the interested reader to Elman, Silvester and Wathen (Reference Elman, Silvester and Wathen2005) and Benzi, Golub and Liesen (Reference Benzi, Golub and Liesen2005), for example. At each time step we have
 $$\begin{eqnarray}\left[\begin{array}{@{}cc@{}}A & B^{T}\\ B & 0\end{array}\right]\left[\begin{array}{@{}c@{}}\boldsymbol{V}\\ \boldsymbol{P}\end{array}\right]=\left[\begin{array}{@{}c@{}}\boldsymbol{F}_{f}\\ \mathbf{0}\end{array}\right]\!,\end{eqnarray}$$
$$\begin{eqnarray}\left[\begin{array}{@{}cc@{}}A & B^{T}\\ B & 0\end{array}\right]\left[\begin{array}{@{}c@{}}\boldsymbol{V}\\ \boldsymbol{P}\end{array}\right]=\left[\begin{array}{@{}c@{}}\boldsymbol{F}_{f}\\ \mathbf{0}\end{array}\right]\!,\end{eqnarray}$$
where
![]() $\boldsymbol{V}$
and
$\boldsymbol{V}$
and
![]() $\boldsymbol{P}$
are the vectors collecting the velocity and pressure unknowns,
$\boldsymbol{P}$
are the vectors collecting the velocity and pressure unknowns,
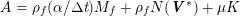 $A=\unicode[STIX]{x1D70C}_{f}(\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6E5}t)M_{f}+\unicode[STIX]{x1D70C}_{f}N(\boldsymbol{V}^{\ast })+\unicode[STIX]{x1D707}K$
(
$A=\unicode[STIX]{x1D70C}_{f}(\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6E5}t)M_{f}+\unicode[STIX]{x1D70C}_{f}N(\boldsymbol{V}^{\ast })+\unicode[STIX]{x1D707}K$
(
![]() $M_{f}$
is the mass matrix,
$M_{f}$
is the mass matrix,
![]() $N$
is the matrix related to the linearized convective term,
$N$
is the matrix related to the linearized convective term,
![]() $K$
is the stiffness matrix),
$K$
is the stiffness matrix),
![]() $\boldsymbol{F}_{f}$
accounts for non-homogeneous Dirichlet and Neumann conditions and the terms coming from time discretization,
$\boldsymbol{F}_{f}$
accounts for non-homogeneous Dirichlet and Neumann conditions and the terms coming from time discretization,
![]() $\unicode[STIX]{x1D6FC}$
depends on the time discretization scheme, and where we have omitted the current temporal index
$\unicode[STIX]{x1D6FC}$
depends on the time discretization scheme, and where we have omitted the current temporal index
![]() $^{n+1}$
.
$^{n+1}$
.
The above non-symmetric linear system can be solved by means of a Krylov method, for example the GMRES method. Suitable preconditioners are required. A classical choice is given by block preconditioners, which again split the solution of the velocity and of the pressure:
 $$\begin{eqnarray}P=\left[\begin{array}{@{}cc@{}}P_{A} & B^{T}\\ 0 & -P_{\unicode[STIX]{x1D6F4}}\end{array}\right]\!.\end{eqnarray}$$
$$\begin{eqnarray}P=\left[\begin{array}{@{}cc@{}}P_{A} & B^{T}\\ 0 & -P_{\unicode[STIX]{x1D6F4}}\end{array}\right]\!.\end{eqnarray}$$
If
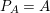 $P_{A}=A$
and
$P_{A}=A$
and
 $P_{\unicode[STIX]{x1D6F4}}=\unicode[STIX]{x1D6F4}=BA^{-1}B^{T}$
(the Schur complement), then the solution is achieved in three GMRES iterations (Elman et al.
Reference Elman, Silvester and Wathen2005). In fact, this choice is equivalent to formally solving the momentum equation for the velocity and substituting its expression in the mass equation. However, in practice this preconditioner is not efficient, since the linear system involving the Schur complement is too onerous,
$P_{\unicode[STIX]{x1D6F4}}=\unicode[STIX]{x1D6F4}=BA^{-1}B^{T}$
(the Schur complement), then the solution is achieved in three GMRES iterations (Elman et al.
Reference Elman, Silvester and Wathen2005). In fact, this choice is equivalent to formally solving the momentum equation for the velocity and substituting its expression in the mass equation. However, in practice this preconditioner is not efficient, since the linear system involving the Schur complement is too onerous,
![]() $\unicode[STIX]{x1D6F4}$
being a full matrix whose explicit construction requires knowledge of
$\unicode[STIX]{x1D6F4}$
being a full matrix whose explicit construction requires knowledge of
![]() $A^{-1}$
. Efficient preconditioners can be obtained by approximating
$A^{-1}$
. Efficient preconditioners can be obtained by approximating
![]() $\unicode[STIX]{x1D6F4}$
(and, if needed,
$\unicode[STIX]{x1D6F4}$
(and, if needed,
![]() $A$
). For low Reynolds numbers (less than 10, say), an effective choice is given by
$A$
). For low Reynolds numbers (less than 10, say), an effective choice is given by
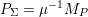 $P_{\unicode[STIX]{x1D6F4}}=\unicode[STIX]{x1D707}^{-1}M_{P}$
, where
$P_{\unicode[STIX]{x1D6F4}}=\unicode[STIX]{x1D707}^{-1}M_{P}$
, where
![]() $M_{P}$
is the pressure mass matrix (or even its diagonal: Elman and Silvester Reference Elman and Silvester1996). Therefore this is a good choice in haemodynamics for small vessels. For increasing Reynolds numbers, the convergence properties of this preconditioner deteriorates since it does not account for the convective term. A better choice for medium and large vessels is given by
$M_{P}$
is the pressure mass matrix (or even its diagonal: Elman and Silvester Reference Elman and Silvester1996). Therefore this is a good choice in haemodynamics for small vessels. For increasing Reynolds numbers, the convergence properties of this preconditioner deteriorates since it does not account for the convective term. A better choice for medium and large vessels is given by
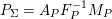 $P_{\unicode[STIX]{x1D6F4}}=A_{P}F_{P}^{-1}M_{P}$
, where
$P_{\unicode[STIX]{x1D6F4}}=A_{P}F_{P}^{-1}M_{P}$
, where
![]() $A_{P}$
is the pressure stiffness matrix, and
$A_{P}$
is the pressure stiffness matrix, and
 $F_{P}=\unicode[STIX]{x1D707}A_{P}+\unicode[STIX]{x1D70C}_{f}N_{P}(\boldsymbol{V}^{\ast })$
, where
$F_{P}=\unicode[STIX]{x1D707}A_{P}+\unicode[STIX]{x1D70C}_{f}N_{P}(\boldsymbol{V}^{\ast })$
, where
![]() $N_{P}$
is the matrix related to the convective term defined on the pressure space (pressure convection-diffusion preconditioner: Elman et al. Reference Elman, Silvester and Wathen2005, Benzi et al. Reference Benzi, Golub and Liesen2005). For the solution of the velocity problem, suitable preconditioners for the advection-reaction-diffusion problem could be introduced. Alternatively, fast solutions such as V-cycle multigrid can be considered (Turek Reference Turek1999).
$N_{P}$
is the matrix related to the convective term defined on the pressure space (pressure convection-diffusion preconditioner: Elman et al. Reference Elman, Silvester and Wathen2005, Benzi et al. Reference Benzi, Golub and Liesen2005). For the solution of the velocity problem, suitable preconditioners for the advection-reaction-diffusion problem could be introduced. Alternatively, fast solutions such as V-cycle multigrid can be considered (Turek Reference Turek1999).
Another class of preconditioners is obtained by an inexact block LU factorization of the fluid matrix. The starting point is the exact factorization
 $$\begin{eqnarray}\left[\begin{array}{@{}cc@{}}A & B^{T}\\ B & 0\end{array}\right]=\left[\begin{array}{@{}cc@{}}A & 0\\ B & -\unicode[STIX]{x1D6F4}\end{array}\right]\left[\begin{array}{@{}cc@{}}I & A^{-1}B^{T}\\ 0 & I\end{array}\right]\!.\end{eqnarray}$$
$$\begin{eqnarray}\left[\begin{array}{@{}cc@{}}A & B^{T}\\ B & 0\end{array}\right]=\left[\begin{array}{@{}cc@{}}A & 0\\ B & -\unicode[STIX]{x1D6F4}\end{array}\right]\left[\begin{array}{@{}cc@{}}I & A^{-1}B^{T}\\ 0 & I\end{array}\right]\!.\end{eqnarray}$$
Again, different preconditioners are obtained by suitable approximations
![]() $\widehat{A}_{1}$
and
$\widehat{A}_{1}$
and
![]() $\widehat{A}_{2}$
of
$\widehat{A}_{2}$
of
![]() $A$
and
$A$
and
![]() $\widehat{\unicode[STIX]{x1D6F4}}$
of
$\widehat{\unicode[STIX]{x1D6F4}}$
of
![]() $\unicode[STIX]{x1D6F4}$
, leading to
$\unicode[STIX]{x1D6F4}$
, leading to
 $$\begin{eqnarray}P=\left[\begin{array}{@{}cc@{}}\widehat{A}_{1} & 0\\ B & -\widehat{\unicode[STIX]{x1D6F4}}\end{array}\right]\left[\begin{array}{@{}cc@{}}I & \widehat{A}_{2}^{-1}B^{T}\\ 0 & I\end{array}\right]\!.\end{eqnarray}$$
$$\begin{eqnarray}P=\left[\begin{array}{@{}cc@{}}\widehat{A}_{1} & 0\\ B & -\widehat{\unicode[STIX]{x1D6F4}}\end{array}\right]\left[\begin{array}{@{}cc@{}}I & \widehat{A}_{2}^{-1}B^{T}\\ 0 & I\end{array}\right]\!.\end{eqnarray}$$
A convenient choice is
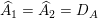 $\widehat{A}_{1}=\widehat{A}_{2}=D_{A}$
and
$\widehat{A}_{1}=\widehat{A}_{2}=D_{A}$
and
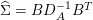 $\widehat{\unicode[STIX]{x1D6F4}}=BD_{A}^{-1}B^{T}$
, where
$\widehat{\unicode[STIX]{x1D6F4}}=BD_{A}^{-1}B^{T}$
, where
![]() $D_{A}$
is the diagonal of
$D_{A}$
is the diagonal of
![]() $A$
(SIMPLE preconditioner: Patankar and Spalding Reference Patankar and Spalding1972, Li and Vuik Reference Li and Vuik2004). Note that in this case
$A$
(SIMPLE preconditioner: Patankar and Spalding Reference Patankar and Spalding1972, Li and Vuik Reference Li and Vuik2004). Note that in this case
![]() $\widehat{\unicode[STIX]{x1D6F4}}$
is sparse and could be explicitly assembled. This is an effective choice when the fluid matrix is diagonally dominant, that is, when small values of
$\widehat{\unicode[STIX]{x1D6F4}}$
is sparse and could be explicitly assembled. This is an effective choice when the fluid matrix is diagonally dominant, that is, when small values of
![]() $\unicode[STIX]{x1D6E5}t$
are used. Another choice is the Yosida preconditioner, where
$\unicode[STIX]{x1D6E5}t$
are used. Another choice is the Yosida preconditioner, where
 $$\begin{eqnarray}\widehat{\unicode[STIX]{x1D6F4}}=\displaystyle \frac{\unicode[STIX]{x1D6E5}t}{\unicode[STIX]{x1D70C}_{f}\unicode[STIX]{x1D6FC}}BM_{f}^{-1}B^{T},\,\widehat{A}_{1}=A\quad \text{and}\quad \widehat{A}_{2}=\displaystyle \frac{\unicode[STIX]{x1D70C}_{f}\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}M_{f}\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\unicode[STIX]{x1D6F4}}=\displaystyle \frac{\unicode[STIX]{x1D6E5}t}{\unicode[STIX]{x1D70C}_{f}\unicode[STIX]{x1D6FC}}BM_{f}^{-1}B^{T},\,\widehat{A}_{1}=A\quad \text{and}\quad \widehat{A}_{2}=\displaystyle \frac{\unicode[STIX]{x1D70C}_{f}\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}M_{f}\end{eqnarray}$$
(Veneziani Reference Veneziani2003). Again, the efficiency deteriorates for increasing
![]() $\unicode[STIX]{x1D6E5}t$
. The Yosida preconditioner was originally introduced as a solver in Veneziani (Reference Veneziani1998b
); see also Quarteroni, Saleri and Veneziani Reference Quarteroni, Saleri and Veneziani1999, Reference Quarteroni, Saleri and Veneziani2000b
. This led to a splitting of the velocity and of the pressure computation, which could be seen as the algebraic counterpart of the Chorin–Temam method (algebraic pressure-correction methods). In particular, we have the following steps:
$\unicode[STIX]{x1D6E5}t$
. The Yosida preconditioner was originally introduced as a solver in Veneziani (Reference Veneziani1998b
); see also Quarteroni, Saleri and Veneziani Reference Quarteroni, Saleri and Veneziani1999, Reference Quarteroni, Saleri and Veneziani2000b
. This led to a splitting of the velocity and of the pressure computation, which could be seen as the algebraic counterpart of the Chorin–Temam method (algebraic pressure-correction methods). In particular, we have the following steps:
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}ll@{}}\displaystyle A\widetilde{\boldsymbol{V}}=\boldsymbol{F}_{f} & \displaystyle \text{computation of the velocity,}\\ \displaystyle \unicode[STIX]{x1D6E5}tBM_{f}^{-1}B^{T}\boldsymbol{P}=B\widetilde{\boldsymbol{V}} & \displaystyle \text{computation of the pressure,}\\ \displaystyle \boldsymbol{V}=\widetilde{\boldsymbol{V}}-\displaystyle \frac{\unicode[STIX]{x1D6E5}t}{\unicode[STIX]{x1D70C}_{f}\unicode[STIX]{x1D6FC}}M_{f}^{-1}B^{T}\boldsymbol{P} & \displaystyle \text{correction of the velocity.}\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}ll@{}}\displaystyle A\widetilde{\boldsymbol{V}}=\boldsymbol{F}_{f} & \displaystyle \text{computation of the velocity,}\\ \displaystyle \unicode[STIX]{x1D6E5}tBM_{f}^{-1}B^{T}\boldsymbol{P}=B\widetilde{\boldsymbol{V}} & \displaystyle \text{computation of the pressure,}\\ \displaystyle \boldsymbol{V}=\widetilde{\boldsymbol{V}}-\displaystyle \frac{\unicode[STIX]{x1D6E5}t}{\unicode[STIX]{x1D70C}_{f}\unicode[STIX]{x1D6FC}}M_{f}^{-1}B^{T}\boldsymbol{P} & \displaystyle \text{correction of the velocity.}\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
Again, an incremental version of the algebraic pressure-correction methods could also be considered (Quarteroni et al. Reference Quarteroni, Saleri and Veneziani2000b ). An extension to spectral methods is provided in Gervasio, Saleri and Veneziani (Reference Gervasio, Saleri and Veneziani2006).
For a recent comparison of the performance of different preconditioners (all described above) used for haemodynamic applications, see Deparis, Grandperrin and Quarteroni (Reference Deparis, Grandperrin and Quarteroni2014).
In healthy conditions, blood flow is mainly laminar. Transitional flow may develop in some pathological instances, or with the assistance of devices. In these circumstances, suitable mesh refinement is often employed, possibly accompanied by the use of turbulence models. We mention the case of stenotic carotid arteries, for which Stroud, Berger and Saloner (Reference Stroud, Berger and Saloner2002) and Grinberg, Yakhot and Karniadakis (Reference Grinberg, Yakhot and Karniadakis2009) use Reynolds-averaged Navier–Stokes (RANS) models, Lee et al. (Reference Lee, Lee, Fischer, Bassiouny and Loth2008), Fischer et al. (Reference Fischer, Loth, Lee, Lee, Smith and Bassiouny2007) and Cheung et al. (Reference Cheung, Wong, Yeoh, Yang, Tu, Beare and Phan2010) use direct numerical simulation (DNS), and Rayz, Berger and Saloner (Reference Rayz, Berger and Saloner2007) and Lancellotti et al. (Reference Lancellotti, Vergara, Valdettaro, Bose and Quarteroni2015) use large eddy simulation (LES). Bazilevs et al. (Reference Bazilevs, Gohean, Hughes, Moser and Zhang2009) use the VMS formulation to describe transitional effects in the ascending aorta under the influence of the left ventricular assist device (LVAD).
In Figure 4.5 we show some examples of numerical results obtained in four real geometries reconstructed from radiological images (see the caption for details). These results highlight the complex pattern of blood flow induced by the geometry and by the heart pulsatility. To highlight the transitional effects in stenotic carotid arteries, Figure 4.5(c) plots the
![]() $Q$
criterion, defined by
$Q$
criterion, defined by
 $$\begin{eqnarray}Q=-\frac{1}{2}\mathop{\sum }_{i,j}S_{ij}^{2}-\unicode[STIX]{x1D6FA}_{ij}^{2},\end{eqnarray}$$
$$\begin{eqnarray}Q=-\frac{1}{2}\mathop{\sum }_{i,j}S_{ij}^{2}-\unicode[STIX]{x1D6FA}_{ij}^{2},\end{eqnarray}$$
where
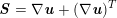 $\boldsymbol{S}=\unicode[STIX]{x1D6FB}\boldsymbol{u}+(\unicode[STIX]{x1D6FB}\boldsymbol{u})^{T}$
and
$\boldsymbol{S}=\unicode[STIX]{x1D6FB}\boldsymbol{u}+(\unicode[STIX]{x1D6FB}\boldsymbol{u})^{T}$
and
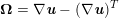 $\boldsymbol{\unicode[STIX]{x1D6FA}}=\unicode[STIX]{x1D6FB}\boldsymbol{u}-(\unicode[STIX]{x1D6FB}\boldsymbol{u})^{T}$
(Lee et al.
Reference Lee, Lee, Fischer, Bassiouny and Loth2008). Positive values of
$\boldsymbol{\unicode[STIX]{x1D6FA}}=\unicode[STIX]{x1D6FB}\boldsymbol{u}-(\unicode[STIX]{x1D6FB}\boldsymbol{u})^{T}$
(Lee et al.
Reference Lee, Lee, Fischer, Bassiouny and Loth2008). Positive values of
![]() $Q$
indicate locations where rotations dominate strain and shear.
$Q$
indicate locations where rotations dominate strain and shear.

Figure 4.5. (a) Velocity vectors in the aneurysm of an abdominal aorta (CT images from the Vascular Surgery and Radiology Divisions at Fondazione IRCSS Cà Granda, Ospedale Maggiore Policlinico, Milan, Italy). (b) Velocity streamlines in a stenotic carotid artery (MRI images from the Vascular Surgery and Radiology Divisions at Ospedale Maggiore Policlinico, Milan). (c) Coherent vortical structures by
![]() $Q$
criterion in a stenotic carotid artery (we show only the regions with
$Q$
criterion in a stenotic carotid artery (we show only the regions with
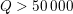 $Q>50\,000$
shaded by the velocity magnitude; CT images from the Vascular Surgery and Radiology Divisions at Ospedale Maggiore Policlinico, Milan). (d) Wall shear stress in an ascending aorta (MRI images from the Cardio Surgery and Radiology Divisions at Ospedale Borgo Trento, Verona, Italy). Numerical results were obtained using the finite element library LifeV, P2/P1 finite elements, the backward Euler scheme for the time discretization with a semi-implicit treatment of the non-linear term, and the Yosida preconditioner. For the stenotic carotid arteries an LES model has been used.
$Q>50\,000$
shaded by the velocity magnitude; CT images from the Vascular Surgery and Radiology Divisions at Ospedale Maggiore Policlinico, Milan). (d) Wall shear stress in an ascending aorta (MRI images from the Cardio Surgery and Radiology Divisions at Ospedale Borgo Trento, Verona, Italy). Numerical results were obtained using the finite element library LifeV, P2/P1 finite elements, the backward Euler scheme for the time discretization with a semi-implicit treatment of the non-linear term, and the Yosida preconditioner. For the stenotic carotid arteries an LES model has been used.
4.6.2 Numerical methods for the vessel wall problem
In this section we review some of the most commonly used numerical approaches for the solution of problem (4.7), endowed with its initial and boundary conditions.
For the time discretization, a popular family of schemes is that of Newmark, which is characterized by two parameters
![]() $\unicode[STIX]{x1D703}$
and
$\unicode[STIX]{x1D703}$
and
![]() $\unicode[STIX]{x1D701}$
(Newmark Reference Newmark1959). The special combination
$\unicode[STIX]{x1D701}$
(Newmark Reference Newmark1959). The special combination
 $\unicode[STIX]{x1D703}=1/2$
and
$\unicode[STIX]{x1D703}=1/2$
and
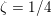 $\unicode[STIX]{x1D701}=1/4$
yields the following semi-discrete form of (4.16) (for simplicity we set
$\unicode[STIX]{x1D701}=1/4$
yields the following semi-discrete form of (4.16) (for simplicity we set
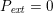 $P_{\mathit{ext}}=0$
and
$P_{\mathit{ext}}=0$
and
![]() $\boldsymbol{h}_{s}=\mathbf{0}$
):
$\boldsymbol{h}_{s}=\mathbf{0}$
):
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D70C}_{s}\int _{\unicode[STIX]{x1D6FA}_{s}}\frac{4\widehat{\boldsymbol{d}}^{n+1}-4\widehat{\boldsymbol{d}}^{n}}{\unicode[STIX]{x1D6E5}t^{2}}\cdot \widehat{\boldsymbol{e}}\text{d}\unicode[STIX]{x1D714}+\int _{\unicode[STIX]{x1D6FA}_{s}}\widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}}^{n+1}):\unicode[STIX]{x1D6FB}\widehat{\boldsymbol{e}}\text{d}\unicode[STIX]{x1D714}+\int _{\unicode[STIX]{x1D6E4}_{\mathit{ext}}}\unicode[STIX]{x1D6FC}_{ST}\widehat{\boldsymbol{d}}^{n+1}\cdot \widehat{\boldsymbol{e}}\text{d}\unicode[STIX]{x1D70E}\nonumber\\ \displaystyle & & \displaystyle \qquad =\unicode[STIX]{x1D70C}_{s}\int _{\unicode[STIX]{x1D6FA}_{s}}\biggl(\frac{4\widehat{\boldsymbol{w}}^{n}}{\unicode[STIX]{x1D6E5}t}+\widehat{\boldsymbol{a}}^{n}\biggr)\cdot \widehat{\boldsymbol{e}}\text{d}\unicode[STIX]{x1D714},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D70C}_{s}\int _{\unicode[STIX]{x1D6FA}_{s}}\frac{4\widehat{\boldsymbol{d}}^{n+1}-4\widehat{\boldsymbol{d}}^{n}}{\unicode[STIX]{x1D6E5}t^{2}}\cdot \widehat{\boldsymbol{e}}\text{d}\unicode[STIX]{x1D714}+\int _{\unicode[STIX]{x1D6FA}_{s}}\widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}}^{n+1}):\unicode[STIX]{x1D6FB}\widehat{\boldsymbol{e}}\text{d}\unicode[STIX]{x1D714}+\int _{\unicode[STIX]{x1D6E4}_{\mathit{ext}}}\unicode[STIX]{x1D6FC}_{ST}\widehat{\boldsymbol{d}}^{n+1}\cdot \widehat{\boldsymbol{e}}\text{d}\unicode[STIX]{x1D70E}\nonumber\\ \displaystyle & & \displaystyle \qquad =\unicode[STIX]{x1D70C}_{s}\int _{\unicode[STIX]{x1D6FA}_{s}}\biggl(\frac{4\widehat{\boldsymbol{w}}^{n}}{\unicode[STIX]{x1D6E5}t}+\widehat{\boldsymbol{a}}^{n}\biggr)\cdot \widehat{\boldsymbol{e}}\text{d}\unicode[STIX]{x1D714},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \widehat{\boldsymbol{w}}^{n+1}=\frac{2}{\unicode[STIX]{x1D6E5}t}(\widehat{\boldsymbol{d}}^{n+1}-\widehat{\boldsymbol{d}}^{n})-\widehat{\boldsymbol{w}}^{n},\quad \widehat{\boldsymbol{a}}^{n+1}=\frac{4}{\unicode[STIX]{x1D6E5}t^{2}}(\widehat{\boldsymbol{d}}^{n+1}-\widehat{\boldsymbol{d}}^{n})-\frac{4}{\unicode[STIX]{x1D6E5}t}\widehat{\boldsymbol{w}}^{n}-\widehat{\boldsymbol{a}}^{n}, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{\boldsymbol{w}}^{n+1}=\frac{2}{\unicode[STIX]{x1D6E5}t}(\widehat{\boldsymbol{d}}^{n+1}-\widehat{\boldsymbol{d}}^{n})-\widehat{\boldsymbol{w}}^{n},\quad \widehat{\boldsymbol{a}}^{n+1}=\frac{4}{\unicode[STIX]{x1D6E5}t^{2}}(\widehat{\boldsymbol{d}}^{n+1}-\widehat{\boldsymbol{d}}^{n})-\frac{4}{\unicode[STIX]{x1D6E5}t}\widehat{\boldsymbol{w}}^{n}-\widehat{\boldsymbol{a}}^{n}, & & \displaystyle \nonumber\end{eqnarray}$$
where
![]() $\widehat{\boldsymbol{w}}^{n+1}$
and
$\widehat{\boldsymbol{w}}^{n+1}$
and
![]() $\widehat{\boldsymbol{a}}^{n+1}$
denote approximations of vessel wall velocity and acceleration, respectively. This method is unconditionally absolutely stable and second-order accurate with respect to
$\widehat{\boldsymbol{a}}^{n+1}$
denote approximations of vessel wall velocity and acceleration, respectively. This method is unconditionally absolutely stable and second-order accurate with respect to
![]() $\unicode[STIX]{x1D6E5}t$
. An extension of Newmark schemes is provided by the generalized-alpha method (Chung and Hulbert Reference Chung and Hulbert1993); see e.g. Isaksen et al. (Reference Isaksen, Bazilevs, Kvamsdal, Zhang, Kaspersen, Waterloo, Romner and Ingebrigtsen2008) for an application to haemodynamics.
$\unicode[STIX]{x1D6E5}t$
. An extension of Newmark schemes is provided by the generalized-alpha method (Chung and Hulbert Reference Chung and Hulbert1993); see e.g. Isaksen et al. (Reference Isaksen, Bazilevs, Kvamsdal, Zhang, Kaspersen, Waterloo, Romner and Ingebrigtsen2008) for an application to haemodynamics.
Space discretization is typically based on finite elements. Whatever the implicit temporal scheme chosen, a system of non-linear algebraic equations is obtained after space and time discretization, that is,
 $$\begin{eqnarray}\frac{\unicode[STIX]{x1D70C}_{s}\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D6E5}t^{2}}M_{s}\boldsymbol{D}+\boldsymbol{\unicode[STIX]{x1D6E4}}(\boldsymbol{D})+\unicode[STIX]{x1D6FC}_{ST}M_{s}^{\mathit{ext}}\boldsymbol{D}=\boldsymbol{G}_{s},\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D70C}_{s}\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D6E5}t^{2}}M_{s}\boldsymbol{D}+\boldsymbol{\unicode[STIX]{x1D6E4}}(\boldsymbol{D})+\unicode[STIX]{x1D6FC}_{ST}M_{s}^{\mathit{ext}}\boldsymbol{D}=\boldsymbol{G}_{s},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FD}$
depends on the time discretization (e.g.
$\unicode[STIX]{x1D6FD}$
depends on the time discretization (e.g.
![]() $\unicode[STIX]{x1D6FD}=4$
for the Newmark method (4.43)),
$\unicode[STIX]{x1D6FD}=4$
for the Newmark method (4.43)),
![]() $\boldsymbol{D}$
is the vector collecting the vessel wall displacement unknowns,
$\boldsymbol{D}$
is the vector collecting the vessel wall displacement unknowns,
![]() $M_{s}$
is the mass matrix,
$M_{s}$
is the mass matrix,
![]() $M_{s}^{\mathit{ext}}$
is the boundary mass matrix related to
$M_{s}^{\mathit{ext}}$
is the boundary mass matrix related to
![]() $\unicode[STIX]{x1D6F4}_{\mathit{ext}}$
,
$\unicode[STIX]{x1D6F4}_{\mathit{ext}}$
,
![]() $\boldsymbol{\unicode[STIX]{x1D6E4}}$
is the non-linear operator defined by
$\boldsymbol{\unicode[STIX]{x1D6E4}}$
is the non-linear operator defined by
 $$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{i}=\int _{\unicode[STIX]{x1D6FA}_{s}}\widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}}):\unicode[STIX]{x1D6FB}\widehat{\boldsymbol{e}_{i}}\text{d}\unicode[STIX]{x1D714},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{i}=\int _{\unicode[STIX]{x1D6FA}_{s}}\widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}}):\unicode[STIX]{x1D6FB}\widehat{\boldsymbol{e}_{i}}\text{d}\unicode[STIX]{x1D714},\end{eqnarray}$$
where
![]() $\widehat{\boldsymbol{e}}_{i}$
is the
$\widehat{\boldsymbol{e}}_{i}$
is the
![]() $i$
th basis function, and
$i$
th basis function, and
![]() $\boldsymbol{G}_{s}$
is the vector related to the right-hand side of the time-discretized equation. Notice that we have omitted the temporal index, which is understood. The above system is linearized by means of the Newton method, obtaining at each time step a sequence of linear systems of the form
$\boldsymbol{G}_{s}$
is the vector related to the right-hand side of the time-discretized equation. Notice that we have omitted the temporal index, which is understood. The above system is linearized by means of the Newton method, obtaining at each time step a sequence of linear systems of the form
 $$\begin{eqnarray}\displaystyle & & \displaystyle \biggl(\frac{\unicode[STIX]{x1D70C}_{s}\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D6E5}t^{2}}M_{s}+T(\boldsymbol{D}_{(k-1)})+\unicode[STIX]{x1D6FC}_{ST}M_{s}^{\mathit{ext}}\biggr)\unicode[STIX]{x1D6FF}\boldsymbol{D}_{(k)}\nonumber\\ \displaystyle & & \displaystyle \qquad =\boldsymbol{G}_{s}-\frac{\unicode[STIX]{x1D70C}_{s}\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D6E5}t^{2}}M_{s}\boldsymbol{D}_{(k-1)}-\boldsymbol{\unicode[STIX]{x1D6E4}}(\boldsymbol{D}_{(k-1)})-\unicode[STIX]{x1D6FC}_{ST}M_{s}^{\mathit{ext}}\boldsymbol{D}_{(k-1)},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \biggl(\frac{\unicode[STIX]{x1D70C}_{s}\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D6E5}t^{2}}M_{s}+T(\boldsymbol{D}_{(k-1)})+\unicode[STIX]{x1D6FC}_{ST}M_{s}^{\mathit{ext}}\biggr)\unicode[STIX]{x1D6FF}\boldsymbol{D}_{(k)}\nonumber\\ \displaystyle & & \displaystyle \qquad =\boldsymbol{G}_{s}-\frac{\unicode[STIX]{x1D70C}_{s}\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D6E5}t^{2}}M_{s}\boldsymbol{D}_{(k-1)}-\boldsymbol{\unicode[STIX]{x1D6E4}}(\boldsymbol{D}_{(k-1)})-\unicode[STIX]{x1D6FC}_{ST}M_{s}^{\mathit{ext}}\boldsymbol{D}_{(k-1)},\nonumber\end{eqnarray}$$
where
![]() $k\geq 1$
is the Newton iteration index, to be solved until convergence occurs. Here
$k\geq 1$
is the Newton iteration index, to be solved until convergence occurs. Here
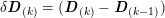 $\unicode[STIX]{x1D6FF}\boldsymbol{D}_{(k)}=(\boldsymbol{D}_{(k)}-\boldsymbol{D}_{(k-1)})$
,
$\unicode[STIX]{x1D6FF}\boldsymbol{D}_{(k)}=(\boldsymbol{D}_{(k)}-\boldsymbol{D}_{(k-1)})$
,
![]() $T$
is the matrix related to the linearization of the first Piola–Kirchhoff tensor, that is,
$T$
is the matrix related to the linearization of the first Piola–Kirchhoff tensor, that is,
 $$\begin{eqnarray}(T)_{ij}=\int _{\unicode[STIX]{x1D6FA}_{s}}(D_{F}\widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}}_{(k-1)}):\unicode[STIX]{x1D6FB}\widehat{\boldsymbol{e}}_{j}):\unicode[STIX]{x1D6FB}\widehat{\boldsymbol{e}}_{i},\end{eqnarray}$$
$$\begin{eqnarray}(T)_{ij}=\int _{\unicode[STIX]{x1D6FA}_{s}}(D_{F}\widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}}_{(k-1)}):\unicode[STIX]{x1D6FB}\widehat{\boldsymbol{e}}_{j}):\unicode[STIX]{x1D6FB}\widehat{\boldsymbol{e}}_{i},\end{eqnarray}$$
where
![]() $D_{F}$
is the Gâteaux derivative with respect to
$D_{F}$
is the Gâteaux derivative with respect to
![]() $\boldsymbol{F}$
.
$\boldsymbol{F}$
.
For the solution of the above linear system, domain decomposition (DD) methods are often used as efficient preconditioners for iterative Krylov methods. Since the matrix
![]() $T$
is symmetric, the conjugate gradient method is usually considered for iterations. Among DD preconditioners,
finite element tearing and interconnect
(FETI) methods (Farhat and Roux Reference Farhat and Roux1991) are very often used in structural mechanics. In particular, all floating FETI methods have been considered for vessel wall problems, for example in Augustin, Holzapfel and Steinbach (Reference Augustin, Holzapfel and Steinbach2014). As in classical FETI methods, Lagrange multipliers are introduced to glue the solution together at the subdomain interfaces. In addition, Lagrange multipliers are also used to prescribe Dirichlet boundary conditions. This simplifies the implementation of the FETI method since all the subdomains are treated in the same way. A variant successfully used for arterial vessel walls is the so-called dual–primal FETI method: see e.g. Balzani et al. (Reference Balzani, Brands, Klawonn, Rheinbach and Schroder2010). Finally, we mention yet another class of DD methods considered for this problem, a two-level overlapping Schwarz method with an energy minimization coarse space: see Dohrmann and Widlund (Reference Dohrmann and Widlund2009).
$T$
is symmetric, the conjugate gradient method is usually considered for iterations. Among DD preconditioners,
finite element tearing and interconnect
(FETI) methods (Farhat and Roux Reference Farhat and Roux1991) are very often used in structural mechanics. In particular, all floating FETI methods have been considered for vessel wall problems, for example in Augustin, Holzapfel and Steinbach (Reference Augustin, Holzapfel and Steinbach2014). As in classical FETI methods, Lagrange multipliers are introduced to glue the solution together at the subdomain interfaces. In addition, Lagrange multipliers are also used to prescribe Dirichlet boundary conditions. This simplifies the implementation of the FETI method since all the subdomains are treated in the same way. A variant successfully used for arterial vessel walls is the so-called dual–primal FETI method: see e.g. Balzani et al. (Reference Balzani, Brands, Klawonn, Rheinbach and Schroder2010). Finally, we mention yet another class of DD methods considered for this problem, a two-level overlapping Schwarz method with an energy minimization coarse space: see Dohrmann and Widlund (Reference Dohrmann and Widlund2009).
In Figure 4.6 we illustrate some examples of numerical results obtained in real geometries reconstructed from radiological images (see the caption for details). These results highlight the anisotropic internal stresses characterizing vascular vessel walls.

Figure 4.6. (a) Von Mises internal stresses in a carotid artery (MRI images from the Vascular Surgery and Radiology Divisions at Ospedale Maggiore Policlinico, Milan, Italy). (b) Von Mises stresses in an abdominal aortic aneurysm (mesh from www.vascularmodel.com/sandbox/doku.php?id=start). Numerical results were obtained using LifeV (carotid artery) and the finite element library redbKIT v2.1 (github.com/redbKIT/redbKIT/releases) (AAA), P2 finite elements, a Newmark unconditionally stable scheme for the time discretization and an exponential vessel wall law.
4.6.3 Numerical methods for the fluid–structure interaction problem
The numerical solution of the coupled FSI problem (4.19) requires us to manage three sources of non-linearities, namely,
-
(i) the fluid domain is unknown (geometric non-linearity),
-
(ii) the fluid subproblem is non-linear (fluid constitutive non-linearity),
-
(iii) the vessel displacement subproblem is non-linear (structure constitutive non-linearity),
together with two different kinds of coupling,
-
(iv) the displacement of the fluid domain at the FS interface needs to match the displacement of the vessel wall (geometric adherence: see (4.19f )),
-
(iiv) the fluid and vessel displacement subproblems are coupled by means of the kinematic and dynamic conditions (4.19c , 4.19d ) (physical coupling).
Arbitrary-Lagrangian formulation.
As for points (i) and (iv), a classical numerical strategy relies on extending the FS interface displacement
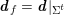 $\boldsymbol{d}_{f}=\boldsymbol{d}|_{\unicode[STIX]{x1D6F4}^{t}}$
to the whole fluid domain, thus associating a displacement with its internal points as well. This is obtained by solving an extra problem for the fluid mesh displacement, usually a harmonic extension of the FS interface datum
$\boldsymbol{d}_{f}=\boldsymbol{d}|_{\unicode[STIX]{x1D6F4}^{t}}$
to the whole fluid domain, thus associating a displacement with its internal points as well. This is obtained by solving an extra problem for the fluid mesh displacement, usually a harmonic extension of the FS interface datum
![]() $\boldsymbol{d}_{f}$
, with homogeneous Dirichlet conditions at
$\boldsymbol{d}_{f}$
, with homogeneous Dirichlet conditions at
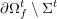 $\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}_{f}^{t}\setminus \unicode[STIX]{x1D6F4}^{t}$
. The fluid domain displacement is then used to move the points of the fluid mesh accordingly, obtaining the new computational fluid domain. With this aim, the Navier–Stokes equations are reformulated on a frame of reference that moves with the fluid mesh. This is neither a Lagrangian description (where the frame moves with the fluid particles) nor an Eulerian description (where a fixed frame would be used). For this reason, it is called the arbitrary Lagrangian–Eulerian (ALE) approach (Hirt, Amsden and Cook Reference Hirt, Amsden and Cook1974, Donea Reference Donea1982). To write the Navier–Stokes equations in an ALE configuration, we use the Reynolds transport formula to express the ALE material time derivative
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}_{f}^{t}\setminus \unicode[STIX]{x1D6F4}^{t}$
. The fluid domain displacement is then used to move the points of the fluid mesh accordingly, obtaining the new computational fluid domain. With this aim, the Navier–Stokes equations are reformulated on a frame of reference that moves with the fluid mesh. This is neither a Lagrangian description (where the frame moves with the fluid particles) nor an Eulerian description (where a fixed frame would be used). For this reason, it is called the arbitrary Lagrangian–Eulerian (ALE) approach (Hirt, Amsden and Cook Reference Hirt, Amsden and Cook1974, Donea Reference Donea1982). To write the Navier–Stokes equations in an ALE configuration, we use the Reynolds transport formula to express the ALE material time derivative
![]() $\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D6FF}t$
of a function
$\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D6FF}t$
of a function
![]() $\boldsymbol{z}$
with respect to the Eulerian derivative, that is,
$\boldsymbol{z}$
with respect to the Eulerian derivative, that is,
 $$\begin{eqnarray}\frac{\unicode[STIX]{x1D6FF}\boldsymbol{z}}{\unicode[STIX]{x1D6FF}t}=\frac{\unicode[STIX]{x2202}\boldsymbol{z}}{\unicode[STIX]{x2202}t}+(\boldsymbol{v}_{f}\cdot \unicode[STIX]{x1D6FB})\boldsymbol{z},\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D6FF}\boldsymbol{z}}{\unicode[STIX]{x1D6FF}t}=\frac{\unicode[STIX]{x2202}\boldsymbol{z}}{\unicode[STIX]{x2202}t}+(\boldsymbol{v}_{f}\cdot \unicode[STIX]{x1D6FB})\boldsymbol{z},\end{eqnarray}$$
where
 $\boldsymbol{v}_{f}=\dot{\boldsymbol{d}}_{f}$
is the velocity of the points of the fluid mesh. Thus, the FSI problem together with its initial and boundary conditions becomes
$\boldsymbol{v}_{f}=\dot{\boldsymbol{d}}_{f}$
is the velocity of the points of the fluid mesh. Thus, the FSI problem together with its initial and boundary conditions becomes
 $$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D70C}_{f}\biggl(\frac{\unicode[STIX]{x1D6FF}\boldsymbol{v}}{\unicode[STIX]{x1D6FF}t}+((\boldsymbol{v}-\boldsymbol{v}_{f})\cdot \unicode[STIX]{x1D6FB})\boldsymbol{v}\biggr)-\unicode[STIX]{x1D6FB}\cdot \boldsymbol{T}_{f}(\boldsymbol{v},p)=\mathbf{0} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f}^{t},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D70C}_{f}\biggl(\frac{\unicode[STIX]{x1D6FF}\boldsymbol{v}}{\unicode[STIX]{x1D6FF}t}+((\boldsymbol{v}-\boldsymbol{v}_{f})\cdot \unicode[STIX]{x1D6FB})\boldsymbol{v}\biggr)-\unicode[STIX]{x1D6FB}\cdot \boldsymbol{T}_{f}(\boldsymbol{v},p)=\mathbf{0} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f}^{t},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D6FB}\cdot \boldsymbol{v}=0 & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f}^{t},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D6FB}\cdot \boldsymbol{v}=0 & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f}^{t},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{v}=\frac{\unicode[STIX]{x2202}\boldsymbol{d}}{\unicode[STIX]{x2202}t} & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{t},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{v}=\frac{\unicode[STIX]{x2202}\boldsymbol{d}}{\unicode[STIX]{x2202}t} & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{t},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{T}_{s}(\boldsymbol{d})\boldsymbol{n}=\boldsymbol{T}_{f}(\boldsymbol{v},p)\boldsymbol{n} & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{t},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{T}_{s}(\boldsymbol{d})\boldsymbol{n}=\boldsymbol{T}_{f}(\boldsymbol{v},p)\boldsymbol{n} & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{t},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D70C}_{s}\frac{\unicode[STIX]{x2202}^{2}\widehat{\boldsymbol{d}}}{\unicode[STIX]{x2202}t^{2}}-\unicode[STIX]{x1D6FB}\cdot \widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}})=\mathbf{0} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{s},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D70C}_{s}\frac{\unicode[STIX]{x2202}^{2}\widehat{\boldsymbol{d}}}{\unicode[STIX]{x2202}t^{2}}-\unicode[STIX]{x1D6FB}\cdot \widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}})=\mathbf{0} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{s},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle \widehat{\boldsymbol{d}}_{f}=\widehat{\boldsymbol{d}} & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \widehat{\boldsymbol{d}}_{f}=\widehat{\boldsymbol{d}} & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle -\triangle \widehat{\boldsymbol{d}}_{f}=\mathbf{0} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle -\triangle \widehat{\boldsymbol{d}}_{f}=\mathbf{0} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f}.\end{eqnarray}$$
 $$\begin{eqnarray}\frac{\unicode[STIX]{x1D6FF}(\boldsymbol{v}_{h}(t,\boldsymbol{x}))}{\unicode[STIX]{x1D6FF}t}=\frac{\unicode[STIX]{x1D6FF}}{\unicode[STIX]{x1D6FF}t}\biggl(\mathop{\sum }_{j}v_{h}^{j}(t)\boldsymbol{\unicode[STIX]{x1D719}}_{j}(\boldsymbol{x}(t))\biggr)=\mathop{\sum }_{j}\frac{\text{d}v_{h}^{j}(t)}{\text{d}t}\boldsymbol{\unicode[STIX]{x1D719}}_{j}(\boldsymbol{x}(t)),\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D6FF}(\boldsymbol{v}_{h}(t,\boldsymbol{x}))}{\unicode[STIX]{x1D6FF}t}=\frac{\unicode[STIX]{x1D6FF}}{\unicode[STIX]{x1D6FF}t}\biggl(\mathop{\sum }_{j}v_{h}^{j}(t)\boldsymbol{\unicode[STIX]{x1D719}}_{j}(\boldsymbol{x}(t))\biggr)=\mathop{\sum }_{j}\frac{\text{d}v_{h}^{j}(t)}{\text{d}t}\boldsymbol{\unicode[STIX]{x1D719}}_{j}(\boldsymbol{x}(t)),\end{eqnarray}$$
since the time variations of the basis functions with respect to the reference domain vanish. This makes the computation of the fluid velocity on the nodes of the fluid mesh easy: see e.g. Nobile (Reference Nobile2001).
For time discretization of (4.44), a common choice is to discretize the fluid and the vessel wall problems with two schemes of equal order (of order
![]() $p$
, say), for example BDF2 or Crank–Nicolson for the fluid and the Newmark scheme (4.43) for the vessel problem.
$p$
, say), for example BDF2 or Crank–Nicolson for the fluid and the Newmark scheme (4.43) for the vessel problem.
Treatment of geometric coupling, geometric adherence and fluid non-linearity.
As for issue (ii) above (constitutive fluid non-linearity), following the approach commonly used for a stand-alone fluid problem, the convective field is usually treated explicitly, by using a suitable extrapolation
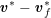 $\boldsymbol{v}^{\ast }-\boldsymbol{v}_{f}^{\ast }$
of order
$\boldsymbol{v}^{\ast }-\boldsymbol{v}_{f}^{\ast }$
of order
![]() $p$
from previous time steps. This choice introduces a CFL-like condition for
$p$
from previous time steps. This choice introduces a CFL-like condition for
![]() $\unicode[STIX]{x1D6E5}t$
to preserve absolute stability, which however is always satisfied for the values of
$\unicode[STIX]{x1D6E5}t$
to preserve absolute stability, which however is always satisfied for the values of
![]() $\unicode[STIX]{x1D6E5}t$
usually considered in haemodynamics. Another common choice in haemodynamics is the explicit treatment of geometric coupling and adherence (issues (i) and (iv) above). In particular, the fluid problem coupled with the structure problem are solved in a domain
$\unicode[STIX]{x1D6E5}t$
usually considered in haemodynamics. Another common choice in haemodynamics is the explicit treatment of geometric coupling and adherence (issues (i) and (iv) above). In particular, the fluid problem coupled with the structure problem are solved in a domain
![]() $\unicode[STIX]{x1D6FA}_{f}^{\ast }$
obtained by a suitable extrapolation from previous time steps of order
$\unicode[STIX]{x1D6FA}_{f}^{\ast }$
obtained by a suitable extrapolation from previous time steps of order
![]() $p$
, and the fluid geometry problem is then solved in sequence (Swim and Seshaiyer Reference Swim and Seshaiyer2006, Fernández, Gerbeau and Grandmont Reference Fernández, Gerbeau and Grandmont2007, Badia, Quaini and Quarteroni Reference Badia, Quaini and Quarteroni2008c
, Nobile and Vergara Reference Nobile and Vergara2008). Again, a limitation on
$p$
, and the fluid geometry problem is then solved in sequence (Swim and Seshaiyer Reference Swim and Seshaiyer2006, Fernández, Gerbeau and Grandmont Reference Fernández, Gerbeau and Grandmont2007, Badia, Quaini and Quarteroni Reference Badia, Quaini and Quarteroni2008c
, Nobile and Vergara Reference Nobile and Vergara2008). Again, a limitation on
![]() $\unicode[STIX]{x1D6E5}t$
is required to ensure absolute stability. In particular, Fernández et al. (Reference Fernández, Gerbeau and Grandmont2007) prove for a model problem that stability is guaranteed under a CFL-like condition. Numerical evidence in real scenarios indicates that this is also a mild condition in the haemodynamics regime: see e.g. Moireau et al. (Reference Moireau, Xiao, Astorino, Figueroa, Chapelle, Taylor and Gerbeau2012) and Nobile, Pozzoli and Vergara (Reference Nobile, Pozzoli and Vergara2014). Based on the considerations above, the following temporal discretization of the FSI problem (4.44) can be considered.
$\unicode[STIX]{x1D6E5}t$
is required to ensure absolute stability. In particular, Fernández et al. (Reference Fernández, Gerbeau and Grandmont2007) prove for a model problem that stability is guaranteed under a CFL-like condition. Numerical evidence in real scenarios indicates that this is also a mild condition in the haemodynamics regime: see e.g. Moireau et al. (Reference Moireau, Xiao, Astorino, Figueroa, Chapelle, Taylor and Gerbeau2012) and Nobile, Pozzoli and Vergara (Reference Nobile, Pozzoli and Vergara2014). Based on the considerations above, the following temporal discretization of the FSI problem (4.44) can be considered.
Explicit scheme for geometric coupling and adherence
For
![]() $n\geq 1$
, at time step
$n\geq 1$
, at time step
![]() $t^{n}$
:
$t^{n}$
:
-
(1) Solve the FSI problem:
where(4.45a ) $$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x1D70C}_{f}\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\boldsymbol{v}^{n}+\unicode[STIX]{x1D70C}_{f}((\boldsymbol{v}^{\ast }-\boldsymbol{v}_{f}^{\ast })\cdot \unicode[STIX]{x1D6FB})\boldsymbol{v}^{n}-\unicode[STIX]{x1D6FB}\cdot \boldsymbol{T}_{f}(\boldsymbol{v}^{n},p^{n})=\boldsymbol{g}_{f}^{n} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f}^{\ast },\end{eqnarray}$$
(4.45b )
$$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x1D70C}_{f}\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\boldsymbol{v}^{n}+\unicode[STIX]{x1D70C}_{f}((\boldsymbol{v}^{\ast }-\boldsymbol{v}_{f}^{\ast })\cdot \unicode[STIX]{x1D6FB})\boldsymbol{v}^{n}-\unicode[STIX]{x1D6FB}\cdot \boldsymbol{T}_{f}(\boldsymbol{v}^{n},p^{n})=\boldsymbol{g}_{f}^{n} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f}^{\ast },\end{eqnarray}$$
(4.45b ) $$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D6FB}\cdot \boldsymbol{v}^{n}=0 & & \displaystyle \displaystyle \quad \text{in }\unicode[STIX]{x1D6FA}_{f}^{\ast },\end{eqnarray}$$
(4.45c )
$$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D6FB}\cdot \boldsymbol{v}^{n}=0 & & \displaystyle \displaystyle \quad \text{in }\unicode[STIX]{x1D6FA}_{f}^{\ast },\end{eqnarray}$$
(4.45c ) $$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{v}^{n}=\frac{\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\boldsymbol{d}^{n}+\boldsymbol{g}_{fs}^{n} & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{\ast },\end{eqnarray}$$
(4.45d )
$$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{v}^{n}=\frac{\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\boldsymbol{d}^{n}+\boldsymbol{g}_{fs}^{n} & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{\ast },\end{eqnarray}$$
(4.45d ) $$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{T}_{s}(\boldsymbol{d}^{n})\boldsymbol{n}^{\ast }=\boldsymbol{T}_{f}(\boldsymbol{v}^{n},p^{n})\boldsymbol{n}^{\ast } & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{\ast },\end{eqnarray}$$
(4.45e )
$$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{T}_{s}(\boldsymbol{d}^{n})\boldsymbol{n}^{\ast }=\boldsymbol{T}_{f}(\boldsymbol{v}^{n},p^{n})\boldsymbol{n}^{\ast } & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{\ast },\end{eqnarray}$$
(4.45e ) $$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x1D70C}_{s}\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D6E5}t^{2}}\widehat{\boldsymbol{d}}^{n}-\unicode[STIX]{x1D6FB}\cdot \widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}}^{n})=\widehat{\boldsymbol{g}}_{s}^{n} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{s},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x1D70C}_{s}\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D6E5}t^{2}}\widehat{\boldsymbol{d}}^{n}-\unicode[STIX]{x1D6FB}\cdot \widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}}^{n})=\widehat{\boldsymbol{g}}_{s}^{n} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{s},\end{eqnarray}$$
 $\unicode[STIX]{x1D6FC}$
still depends on the time discretization scheme, and account for the terms at previous time steps coming from time discretizations of order
$\unicode[STIX]{x1D6FC}$
still depends on the time discretization scheme, and account for the terms at previous time steps coming from time discretizations of order $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{g}_{f}^{n}=\boldsymbol{g}_{f}^{n}(\boldsymbol{v}^{n-1},\boldsymbol{v}^{n-2},\ldots ), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \boldsymbol{g}_{s}^{n}=\boldsymbol{g}_{s}^{n}(\boldsymbol{d}^{n-1},\boldsymbol{d}^{n-2},\ldots ), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \boldsymbol{g}_{fs}^{n} & \displaystyle =\boldsymbol{g}_{fs}^{n}(\boldsymbol{d}^{n-1},\boldsymbol{d}^{n-2},\ldots )\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{g}_{f}^{n}=\boldsymbol{g}_{f}^{n}(\boldsymbol{v}^{n-1},\boldsymbol{v}^{n-2},\ldots ), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \boldsymbol{g}_{s}^{n}=\boldsymbol{g}_{s}^{n}(\boldsymbol{d}^{n-1},\boldsymbol{d}^{n-2},\ldots ), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \boldsymbol{g}_{fs}^{n} & \displaystyle =\boldsymbol{g}_{fs}^{n}(\boldsymbol{d}^{n-1},\boldsymbol{d}^{n-2},\ldots )\nonumber\end{eqnarray}$$
 $p$
of the corresponding equations (4.44a
), (4.44e
) and (4.44c
), respectively.
$p$
of the corresponding equations (4.44a
), (4.44e
) and (4.44c
), respectively.
-
(2) Then, solve the fluid geometry problem,
and build(4.46a ) $$\begin{eqnarray}\displaystyle \displaystyle -\triangle \widehat{\boldsymbol{d}}_{f}^{n}=\mathbf{0} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f},\end{eqnarray}$$
(4.46b )
$$\begin{eqnarray}\displaystyle \displaystyle -\triangle \widehat{\boldsymbol{d}}_{f}^{n}=\mathbf{0} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f},\end{eqnarray}$$
(4.46b ) $$\begin{eqnarray}\displaystyle \displaystyle \widehat{\boldsymbol{d}}_{f}^{n}=\widehat{\boldsymbol{d}}^{n} & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \widehat{\boldsymbol{d}}_{f}^{n}=\widehat{\boldsymbol{d}}^{n} & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4},\end{eqnarray}$$
 $\unicode[STIX]{x1D6FA}_{f}^{\ast }$
accordingly.
$\unicode[STIX]{x1D6FA}_{f}^{\ast }$
accordingly.
In the above substeps, the FSI problem (4.45) is still coupled by means of the physical coupling given by the interface conditions (4.45c
, 4.45d
): see issue (v) above. For the solution of this problem, both partitioned and monolithic procedures have been successfully considered so far in haemodynamics. In partitioned schemes, the fluid and vessel wall subproblems are solved separately, one or more times per time step. Each of the two problems is equipped with a suitable boundary condition at the FS interface
![]() $\unicode[STIX]{x1D6F4}^{\ast }$
derived by splitting the physical interface conditions (4.45c
, 4.45d
).
$\unicode[STIX]{x1D6F4}^{\ast }$
derived by splitting the physical interface conditions (4.45c
, 4.45d
).
Partitioned algorithms of explicit type.
From the computational point of view, an attractive class of partitioned schemes is that of the loosely coupled algorithms where the two subproblems are solved only once per time step. The classic loosely coupled algorithm, widely used in aerodynamics (Piperno and Farhat Reference Piperno and Farhat2001), is the explicit Dirichlet–Neumann scheme, where condition (4.45c ) is prescribed explicitly as a Dirichlet condition in the fluid subproblem, whereas condition (4.45d ) is prescribed as a Neumann condition on the vessel wall subproblem, leading to the following.
Explicit Dirichlet–Neumann scheme
For
![]() $n\geq 1$
, at time step
$n\geq 1$
, at time step
![]() $t^{n}$
:
$t^{n}$
:
-
(1) Solve the fluid Oseen problem with a Dirichlet condition at the FS interface:
(4.47a ) $$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x1D70C}_{f}\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\boldsymbol{v}^{n}+\unicode[STIX]{x1D70C}_{f}((\boldsymbol{v}^{\ast }-\boldsymbol{v}_{f}^{\ast })\cdot \unicode[STIX]{x1D6FB})\boldsymbol{v}^{n}-\unicode[STIX]{x1D6FB}\cdot \boldsymbol{T}_{f}(\boldsymbol{v}^{n},p^{n})=\boldsymbol{g}_{f}^{n} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f}^{\ast },\end{eqnarray}$$
(4.47b )
$$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x1D70C}_{f}\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\boldsymbol{v}^{n}+\unicode[STIX]{x1D70C}_{f}((\boldsymbol{v}^{\ast }-\boldsymbol{v}_{f}^{\ast })\cdot \unicode[STIX]{x1D6FB})\boldsymbol{v}^{n}-\unicode[STIX]{x1D6FB}\cdot \boldsymbol{T}_{f}(\boldsymbol{v}^{n},p^{n})=\boldsymbol{g}_{f}^{n} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f}^{\ast },\end{eqnarray}$$
(4.47b ) $$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D6FB}\cdot \boldsymbol{v}^{n}=0 & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f}^{\ast },\end{eqnarray}$$
(4.47c )
$$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D6FB}\cdot \boldsymbol{v}^{n}=0 & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f}^{\ast },\end{eqnarray}$$
(4.47c ) $$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{v}^{n}=\frac{\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\boldsymbol{d}^{n-1}+\boldsymbol{g}_{fs}^{n-1} & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{v}^{n}=\frac{\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\boldsymbol{d}^{n-1}+\boldsymbol{g}_{fs}^{n-1} & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{\ast }.\end{eqnarray}$$
-
(2) Then, solve the non-linear vessel wall problem with a Neumann condition at the FS interface:
(4.48a ) $$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x1D70C}_{s}\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D6E5}t^{2}}\widehat{\boldsymbol{d}}^{n}-\unicode[STIX]{x1D6FB}\cdot \widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}}^{n})=\widehat{\boldsymbol{g}}_{s}^{n} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{s},\end{eqnarray}$$
(4.48b )
$$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x1D70C}_{s}\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D6E5}t^{2}}\widehat{\boldsymbol{d}}^{n}-\unicode[STIX]{x1D6FB}\cdot \widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}}^{n})=\widehat{\boldsymbol{g}}_{s}^{n} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{s},\end{eqnarray}$$
(4.48b ) $$\begin{eqnarray}\displaystyle \displaystyle \widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}}^{n})\widehat{\boldsymbol{n}}=\widehat{\boldsymbol{T}}_{f}(\widehat{\boldsymbol{v}}^{n},\widehat{p}^{n})\widehat{\boldsymbol{n}} & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}}^{n})\widehat{\boldsymbol{n}}=\widehat{\boldsymbol{T}}_{f}(\widehat{\boldsymbol{v}}^{n},\widehat{p}^{n})\widehat{\boldsymbol{n}} & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4}.\end{eqnarray}$$
Note that the time-discretized kinematic condition (4.47c ) differs from (4.45c ) since now we are considering an explicit Dirichlet condition for the fluid subproblem, so the right-hand side is computed at the previous time step.
A ‘parallel’ version of this scheme is obtained by replacing
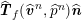 $\widehat{\boldsymbol{T}}_{f}(\widehat{\boldsymbol{v}}^{n},\widehat{p}^{n})\widehat{\boldsymbol{n}}$
with
$\widehat{\boldsymbol{T}}_{f}(\widehat{\boldsymbol{v}}^{n},\widehat{p}^{n})\widehat{\boldsymbol{n}}$
with
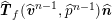 $\widehat{\boldsymbol{T}}_{f}(\widehat{\boldsymbol{v}}^{n-1},\widehat{p}^{n-1})\widehat{\boldsymbol{n}}$
in (4.48b
). Notice that in the monolithic FSI problem (4.45), the dynamic continuity condition (4.45d
) is written in the current configuration
$\widehat{\boldsymbol{T}}_{f}(\widehat{\boldsymbol{v}}^{n-1},\widehat{p}^{n-1})\widehat{\boldsymbol{n}}$
in (4.48b
). Notice that in the monolithic FSI problem (4.45), the dynamic continuity condition (4.45d
) is written in the current configuration
![]() $\unicode[STIX]{x1D6F4}^{\ast }$
, whereas for the structure subproblem alone (4.48) is written in the reference configuration
$\unicode[STIX]{x1D6F4}^{\ast }$
, whereas for the structure subproblem alone (4.48) is written in the reference configuration
![]() $\unicode[STIX]{x1D6F4}$
. Accordingly, in what follows the structure interface quantities will be written in the current configuration in monolithic FSI problems and in the reference configuration when the structure problem is uncoupled in view of a partitioned scheme.
$\unicode[STIX]{x1D6F4}$
. Accordingly, in what follows the structure interface quantities will be written in the current configuration in monolithic FSI problems and in the reference configuration when the structure problem is uncoupled in view of a partitioned scheme.
Unfortunately, the explicit Dirichlet–Neumann scheme can be unconditionally absolutely unstable. In particular, Causin, Gerbeau and Nobile (Reference Causin, Gerbeau and Nobile2005) prove that this happens if the fluid and structure densities are comparable, which is precisely the case for haemodynamics. This is due to the so-called high added mass effect. See also Forster, Wall and Ramm (Reference Forster, Wall and Ramm2007) and Nobile and Vergara (Reference Nobile and Vergara2012).
Stable loosely coupled algorithms have been introduced recently. To this end, in the FSI problem (4.45) the interface conditions (4.45c , 4.45d ) are replaced by two linear independent combinations
 $$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D70E}_{f}\boldsymbol{v}^{n}+\boldsymbol{T}_{f}(\boldsymbol{v}^{n},p^{n})\boldsymbol{n}^{\ast }=\unicode[STIX]{x1D70E}_{f}\biggl(\frac{\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\boldsymbol{d}^{n}+\boldsymbol{g}_{fs}^{n}\biggr)+\boldsymbol{T}_{s}(\boldsymbol{d}^{n})\boldsymbol{n}^{\ast } & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{\ast },\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D70E}_{f}\boldsymbol{v}^{n}+\boldsymbol{T}_{f}(\boldsymbol{v}^{n},p^{n})\boldsymbol{n}^{\ast }=\unicode[STIX]{x1D70E}_{f}\biggl(\frac{\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\boldsymbol{d}^{n}+\boldsymbol{g}_{fs}^{n}\biggr)+\boldsymbol{T}_{s}(\boldsymbol{d}^{n})\boldsymbol{n}^{\ast } & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{\ast },\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D70E}_{s}\biggl(\frac{\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\boldsymbol{d}^{n}+\boldsymbol{g}_{fs}^{n}\biggr)+\boldsymbol{T}_{s}(\boldsymbol{d}^{n})\boldsymbol{n}^{\ast }=\unicode[STIX]{x1D70E}_{s}\boldsymbol{v}^{n}+\boldsymbol{T}_{f}(\boldsymbol{v}^{n},p^{n})\boldsymbol{n}^{\ast } & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{\ast },\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D70E}_{s}\biggl(\frac{\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\boldsymbol{d}^{n}+\boldsymbol{g}_{fs}^{n}\biggr)+\boldsymbol{T}_{s}(\boldsymbol{d}^{n})\boldsymbol{n}^{\ast }=\unicode[STIX]{x1D70E}_{s}\boldsymbol{v}^{n}+\boldsymbol{T}_{f}(\boldsymbol{v}^{n},p^{n})\boldsymbol{n}^{\ast } & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{\ast },\end{eqnarray}$$
 $\unicode[STIX]{x1D70E}_{f}\neq \unicode[STIX]{x1D70E}_{s}$
are, in general, two functions of space and time. This naturally leads to the following.
$\unicode[STIX]{x1D70E}_{f}\neq \unicode[STIX]{x1D70E}_{s}$
are, in general, two functions of space and time. This naturally leads to the following.
Explicit Robin–Robin scheme
For
![]() $n\geq 1$
, at time step
$n\geq 1$
, at time step
![]() $t^{n}$
:
$t^{n}$
:
-
(1) Solve the Oseen problem with a Robin condition at the FS interface:
(4.50a ) $$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x1D70C}_{f}\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\boldsymbol{v}^{n}+\unicode[STIX]{x1D70C}_{f}((\boldsymbol{v}^{\ast }-\boldsymbol{v}_{f}^{\ast })\cdot \unicode[STIX]{x1D6FB})\boldsymbol{v}^{n} & & \displaystyle \nonumber\\ \displaystyle \displaystyle \qquad -\,\unicode[STIX]{x1D6FB}\cdot \boldsymbol{T}_{f}(\boldsymbol{v}^{n},p^{n})=\boldsymbol{g}_{f}^{n} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f}^{\ast },\end{eqnarray}$$
(4.50b )
$$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x1D70C}_{f}\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\boldsymbol{v}^{n}+\unicode[STIX]{x1D70C}_{f}((\boldsymbol{v}^{\ast }-\boldsymbol{v}_{f}^{\ast })\cdot \unicode[STIX]{x1D6FB})\boldsymbol{v}^{n} & & \displaystyle \nonumber\\ \displaystyle \displaystyle \qquad -\,\unicode[STIX]{x1D6FB}\cdot \boldsymbol{T}_{f}(\boldsymbol{v}^{n},p^{n})=\boldsymbol{g}_{f}^{n} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f}^{\ast },\end{eqnarray}$$
(4.50b ) $$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D6FB}\cdot \boldsymbol{v}^{n}=0 & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f}^{\ast },\end{eqnarray}$$
(4.50c )
$$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D6FB}\cdot \boldsymbol{v}^{n}=0 & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f}^{\ast },\end{eqnarray}$$
(4.50c ) $$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D70E}_{f}\boldsymbol{v}^{n}+\boldsymbol{T}_{f}(\boldsymbol{v}^{n},p^{n})\boldsymbol{n}^{\ast } & & \displaystyle \nonumber\\ \displaystyle \qquad \unicode[STIX]{x1D70E}_{f}\biggl(\frac{\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\boldsymbol{d}^{n-1}+\boldsymbol{g}_{fs}^{n-1}\biggr)+\boldsymbol{T}_{s}(\boldsymbol{d}^{n-1})\boldsymbol{n}^{\ast } & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D70E}_{f}\boldsymbol{v}^{n}+\boldsymbol{T}_{f}(\boldsymbol{v}^{n},p^{n})\boldsymbol{n}^{\ast } & & \displaystyle \nonumber\\ \displaystyle \qquad \unicode[STIX]{x1D70E}_{f}\biggl(\frac{\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\boldsymbol{d}^{n-1}+\boldsymbol{g}_{fs}^{n-1}\biggr)+\boldsymbol{T}_{s}(\boldsymbol{d}^{n-1})\boldsymbol{n}^{\ast } & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{\ast }.\end{eqnarray}$$
-
(2) Then, solve the non-linear vessel wall problem with a Robin condition at the FS interface:
(4.51a ) $$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x1D70C}_{s}\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D6E5}t^{2}}\widehat{\boldsymbol{d}}^{n}-\unicode[STIX]{x1D6FB}\cdot \widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}}^{n})=\widehat{\boldsymbol{g}}_{s}^{n} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{s},\end{eqnarray}$$
(4.51b )
$$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x1D70C}_{s}\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D6E5}t^{2}}\widehat{\boldsymbol{d}}^{n}-\unicode[STIX]{x1D6FB}\cdot \widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}}^{n})=\widehat{\boldsymbol{g}}_{s}^{n} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{s},\end{eqnarray}$$
(4.51b ) $$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x1D70E}_{s}\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\widehat{\boldsymbol{d}}^{n}+\widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}}^{n})\widehat{\boldsymbol{n}}=\unicode[STIX]{x1D70E}_{s}\widehat{\boldsymbol{v}}^{n}+\widehat{\boldsymbol{T}}_{f}(\widehat{\boldsymbol{v}}^{n},\widehat{p}^{n})\widehat{\boldsymbol{n}}-\unicode[STIX]{x1D70E}_{s}\widehat{\boldsymbol{g}}_{fs}^{n} & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x1D70E}_{s}\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\widehat{\boldsymbol{d}}^{n}+\widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}}^{n})\widehat{\boldsymbol{n}}=\unicode[STIX]{x1D70E}_{s}\widehat{\boldsymbol{v}}^{n}+\widehat{\boldsymbol{T}}_{f}(\widehat{\boldsymbol{v}}^{n},\widehat{p}^{n})\widehat{\boldsymbol{n}}-\unicode[STIX]{x1D70E}_{s}\widehat{\boldsymbol{g}}_{fs}^{n} & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4}.\end{eqnarray}$$
Burman and Fernández (Reference Burman and Fernández2009) propose a discontinuous Galerkin (DG)-like mortaring of the interface coupling conditions (4.45c
, 4.45d
). The corresponding block Gauss–Seidel explicit algorithm could be reinterpreted as an explicit Dirichlet–Robin scheme, where in (4.50c
, 4.51b
) we have
 $\unicode[STIX]{x1D70E}_{f}=+\infty$
,
$\unicode[STIX]{x1D70E}_{f}=+\infty$
,
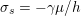 $\unicode[STIX]{x1D70E}_{s}=-\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D707}/h$
, where
$\unicode[STIX]{x1D70E}_{s}=-\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D707}/h$
, where
![]() $\unicode[STIX]{x1D6FE}$
is the DG penalty parameter. Burman and Fernández show that the DG interface penalty and the viscous dissipation are not able to control the pressure fluctuations at the FS interface appearing in the discrete energy estimate. For this reason, they propose adding to the fluid problem a consistent stabilization term penalizing the pressure fluctuations, which is proved to be absolutely stable under a CFL-like condition. Banks, Henshaw and Schwendeman (Reference Banks, Henshaw and Schwendeman2014) have introduced a stable explicit Robin–Robin scheme, setting the parameters in the Robin interface conditions (4.50c
, 4.51b
) after analysing the incoming and outgoing characteristic variables of the vessel wall problem. In particular, the above parameters are defined in terms of the outgoing characteristic variable for the fluid subproblem and in terms of the incoming characteristic variable for the vessel wall subproblem. For linear elasticity, the following values are obtained:
$\unicode[STIX]{x1D6FE}$
is the DG penalty parameter. Burman and Fernández show that the DG interface penalty and the viscous dissipation are not able to control the pressure fluctuations at the FS interface appearing in the discrete energy estimate. For this reason, they propose adding to the fluid problem a consistent stabilization term penalizing the pressure fluctuations, which is proved to be absolutely stable under a CFL-like condition. Banks, Henshaw and Schwendeman (Reference Banks, Henshaw and Schwendeman2014) have introduced a stable explicit Robin–Robin scheme, setting the parameters in the Robin interface conditions (4.50c
, 4.51b
) after analysing the incoming and outgoing characteristic variables of the vessel wall problem. In particular, the above parameters are defined in terms of the outgoing characteristic variable for the fluid subproblem and in terms of the incoming characteristic variable for the vessel wall subproblem. For linear elasticity, the following values are obtained:
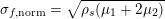 $\unicode[STIX]{x1D70E}_{f,\text{norm}}=\sqrt{\unicode[STIX]{x1D70C}_{s}(\unicode[STIX]{x1D707}_{1}+2\unicode[STIX]{x1D707}_{2})}$
and
$\unicode[STIX]{x1D70E}_{f,\text{norm}}=\sqrt{\unicode[STIX]{x1D70C}_{s}(\unicode[STIX]{x1D707}_{1}+2\unicode[STIX]{x1D707}_{2})}$
and
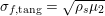 $\unicode[STIX]{x1D70E}_{f,\text{tang}}=\sqrt{\unicode[STIX]{x1D70C}_{s}\unicode[STIX]{x1D707}_{2}}$
in the normal and tangential direction, respectively (
$\unicode[STIX]{x1D70E}_{f,\text{tang}}=\sqrt{\unicode[STIX]{x1D70C}_{s}\unicode[STIX]{x1D707}_{2}}$
in the normal and tangential direction, respectively (
![]() $\unicode[STIX]{x1D707}_{1}$
and
$\unicode[STIX]{x1D707}_{1}$
and
![]() $\unicode[STIX]{x1D707}_{2}$
are the Lamé constants), and
$\unicode[STIX]{x1D707}_{2}$
are the Lamé constants), and
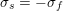 $\unicode[STIX]{x1D70E}_{s}=-\unicode[STIX]{x1D70E}_{f}$
. This choice allows the travelling information contained in the characteristic variables to provide a tighter coupling of the fluid and structure problems than that enforced by (4.45c
, 4.45d
).
$\unicode[STIX]{x1D70E}_{s}=-\unicode[STIX]{x1D70E}_{f}$
. This choice allows the travelling information contained in the characteristic variables to provide a tighter coupling of the fluid and structure problems than that enforced by (4.45c
, 4.45d
).
Partitioned algorithms of semi-implicit type.
Fernández et al. (Reference Fernández, Gerbeau and Grandmont2007) prove that to achieve stability without stabilization terms for the Dirichlet–Neumann scheme, an implicit coupling between the fluid pressure and the vessel wall displacement is required. In particular, a projection scheme is used where the fluid ALE-advection-diffusion step is solved explicitly, whereas the fluid pressure and vessel wall subproblems are coupled and solved in an iterative framework until convergence occurs (see also Astorino and Grandmont Reference Astorino and Grandmont2009 for a convergence analysis).
Semi-implicit pressure-vessel wall coupled scheme
For
![]() $n\geq 1$
, at time step
$n\geq 1$
, at time step
![]() $t^{n}$
:
$t^{n}$
:
-
(1) Solve the ALE-advection-diffusion problem with a Dirichlet condition at the FS interface:
(4.52a ) $$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x1D70C}_{f}\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\widetilde{\boldsymbol{v}}^{n}+\unicode[STIX]{x1D70C}_{f}((\boldsymbol{v}^{\ast }-\boldsymbol{v}_{f}^{\ast })\cdot \unicode[STIX]{x1D6FB})\widetilde{\boldsymbol{v}}^{n} & & \displaystyle \nonumber\\ \displaystyle \qquad -\,\unicode[STIX]{x1D6FB}\cdot \unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FB}\widetilde{\boldsymbol{v}}^{n}+(\unicode[STIX]{x1D6FB}\widetilde{\boldsymbol{v}}^{n})^{T})=\boldsymbol{g}_{f}^{n} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f}^{\ast },\end{eqnarray}$$
(4.52b )
$$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x1D70C}_{f}\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\widetilde{\boldsymbol{v}}^{n}+\unicode[STIX]{x1D70C}_{f}((\boldsymbol{v}^{\ast }-\boldsymbol{v}_{f}^{\ast })\cdot \unicode[STIX]{x1D6FB})\widetilde{\boldsymbol{v}}^{n} & & \displaystyle \nonumber\\ \displaystyle \qquad -\,\unicode[STIX]{x1D6FB}\cdot \unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FB}\widetilde{\boldsymbol{v}}^{n}+(\unicode[STIX]{x1D6FB}\widetilde{\boldsymbol{v}}^{n})^{T})=\boldsymbol{g}_{f}^{n} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f}^{\ast },\end{eqnarray}$$
(4.52b ) $$\begin{eqnarray}\displaystyle \displaystyle \widetilde{\boldsymbol{v}}^{n}=\frac{\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\boldsymbol{d}^{n-1}+\boldsymbol{g}_{fs}^{n-1} & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \widetilde{\boldsymbol{v}}^{n}=\frac{\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\boldsymbol{d}^{n-1}+\boldsymbol{g}_{fs}^{n-1} & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{\ast }.\end{eqnarray}$$
-
(2) Then, solve the coupled pressure-vessel wall problem. To this end, introduce the following iterations on index
 $k\geq 1$
.
$k\geq 1$
.-
(a) Solve the pressure problem with a Neumann condition at the FS interface:
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}ll@{}}\displaystyle \triangle p_{(k)}^{n}=\frac{\unicode[STIX]{x1D70C}_{f}\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\unicode[STIX]{x1D6FB}\cdot \widetilde{\boldsymbol{v}}_{(k)}^{n} & \displaystyle \quad \text{in }\unicode[STIX]{x1D6FA}_{f}^{\ast },\\ \displaystyle \frac{\unicode[STIX]{x2202}p_{(k)}^{n}}{\unicode[STIX]{x2202}\boldsymbol{n}^{\ast }}=\frac{\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\boldsymbol{d}_{(k-1)}^{n}+\boldsymbol{g}_{fs}^{n} & \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{\ast }.\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}ll@{}}\displaystyle \triangle p_{(k)}^{n}=\frac{\unicode[STIX]{x1D70C}_{f}\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\unicode[STIX]{x1D6FB}\cdot \widetilde{\boldsymbol{v}}_{(k)}^{n} & \displaystyle \quad \text{in }\unicode[STIX]{x1D6FA}_{f}^{\ast },\\ \displaystyle \frac{\unicode[STIX]{x2202}p_{(k)}^{n}}{\unicode[STIX]{x2202}\boldsymbol{n}^{\ast }}=\frac{\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\boldsymbol{d}_{(k-1)}^{n}+\boldsymbol{g}_{fs}^{n} & \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{\ast }.\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
-
(b) Then, solve the non-linear vessel wall problem with a Neumann condition at the FS interface:
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}ll@{}}\displaystyle \frac{\unicode[STIX]{x1D70C}_{s}\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D6E5}t^{2}}\widehat{\boldsymbol{d}}_{(k)}^{n}-\unicode[STIX]{x1D6FB}\cdot \widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}}_{(k)}^{n})=\widehat{\boldsymbol{g}}_{s}^{n} & \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{s},\\ \displaystyle \widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}}_{(k)}^{n})\widehat{\boldsymbol{n}}=\widehat{\boldsymbol{T}}_{f}(\widehat{\widetilde{\boldsymbol{v}}}^{n},\widehat{p}_{(k)}^{n})\widehat{\boldsymbol{n}} & \displaystyle \text{on }\unicode[STIX]{x1D6F4}.\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}ll@{}}\displaystyle \frac{\unicode[STIX]{x1D70C}_{s}\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D6E5}t^{2}}\widehat{\boldsymbol{d}}_{(k)}^{n}-\unicode[STIX]{x1D6FB}\cdot \widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}}_{(k)}^{n})=\widehat{\boldsymbol{g}}_{s}^{n} & \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{s},\\ \displaystyle \widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}}_{(k)}^{n})\widehat{\boldsymbol{n}}=\widehat{\boldsymbol{T}}_{f}(\widehat{\widetilde{\boldsymbol{v}}}^{n},\widehat{p}_{(k)}^{n})\widehat{\boldsymbol{n}} & \displaystyle \text{on }\unicode[STIX]{x1D6F4}.\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
-
Astorino, Chouly and Fernández (Reference Astorino, Chouly and Fernández2009) apply the DG mortaring approach to this projection scheme, leading to a Robin–Robin-like scheme. An algebraic version of the projection scheme proposed by Fernández et al. (Reference Fernández, Gerbeau and Grandmont2007) is introduced in Badia et al. (Reference Badia, Quaini and Quarteroni2008c ).
Partitioned algorithms of implicit type.
More generally, a fully implicit treatment of (4.45c , 4.45d ) (or (4.49)) by means of partitioned algorithms is often considered. In this case, the fluid and vessel wall subproblems are solved iteratively until the whole interface conditions are satisfied within a prescribed tolerance. A general scheme is given by the following.
Implicit Robin–Robin scheme
For
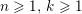 $n\geq 1,\,k\geq 1$
, at time step
$n\geq 1,\,k\geq 1$
, at time step
![]() $t^{n}$
/iteration
$t^{n}$
/iteration
![]() $k$
:
$k$
:
-
(1) Solve the Oseen problem with a Robin condition at the FS interface:
(4.55a ) $$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x1D70C}_{f}\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\boldsymbol{v}_{(k)}^{n}+\unicode[STIX]{x1D70C}_{f}((\boldsymbol{v}^{\ast }-\boldsymbol{v}_{f}^{\ast })\cdot \unicode[STIX]{x1D6FB})\boldsymbol{v}_{(k)}^{n} & & \displaystyle \nonumber\\ \displaystyle \displaystyle \qquad -\,\unicode[STIX]{x1D6FB}\cdot \boldsymbol{T}_{f}(\boldsymbol{v}_{(k)}^{n},p_{(k)}^{n})=\boldsymbol{g}_{f}^{n} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f}^{\ast },\end{eqnarray}$$
(4.55b )
$$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x1D70C}_{f}\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\boldsymbol{v}_{(k)}^{n}+\unicode[STIX]{x1D70C}_{f}((\boldsymbol{v}^{\ast }-\boldsymbol{v}_{f}^{\ast })\cdot \unicode[STIX]{x1D6FB})\boldsymbol{v}_{(k)}^{n} & & \displaystyle \nonumber\\ \displaystyle \displaystyle \qquad -\,\unicode[STIX]{x1D6FB}\cdot \boldsymbol{T}_{f}(\boldsymbol{v}_{(k)}^{n},p_{(k)}^{n})=\boldsymbol{g}_{f}^{n} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f}^{\ast },\end{eqnarray}$$
(4.55b ) $$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D6FB}\cdot \boldsymbol{v}_{(k)}^{n}=0 & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f}^{\ast },\end{eqnarray}$$
(4.55c )
$$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D6FB}\cdot \boldsymbol{v}_{(k)}^{n}=0 & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f}^{\ast },\end{eqnarray}$$
(4.55c ) $$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D70E}_{f}\boldsymbol{v}_{(k)}^{n}+\boldsymbol{T}_{f}(\boldsymbol{v}_{(k)}^{n},p_{(k)}^{n})\boldsymbol{n}^{\ast } & & \displaystyle \nonumber\\ \displaystyle \displaystyle \qquad =\unicode[STIX]{x1D70E}_{f}\biggl(\frac{\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\boldsymbol{d}_{(k-1)}^{n}+\boldsymbol{g}_{fs}^{n}\biggr)+\boldsymbol{T}_{s}(\boldsymbol{d}_{(k-1)}^{n})\boldsymbol{n}^{\ast } & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D70E}_{f}\boldsymbol{v}_{(k)}^{n}+\boldsymbol{T}_{f}(\boldsymbol{v}_{(k)}^{n},p_{(k)}^{n})\boldsymbol{n}^{\ast } & & \displaystyle \nonumber\\ \displaystyle \displaystyle \qquad =\unicode[STIX]{x1D70E}_{f}\biggl(\frac{\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\boldsymbol{d}_{(k-1)}^{n}+\boldsymbol{g}_{fs}^{n}\biggr)+\boldsymbol{T}_{s}(\boldsymbol{d}_{(k-1)}^{n})\boldsymbol{n}^{\ast } & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{\ast }.\end{eqnarray}$$
-
(2) Then, solve the non-linear vessel wall problem with a Robin condition at the FS interface:
(4.56a ) $$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x1D70C}_{s}\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D6E5}t^{2}}\widehat{\boldsymbol{d}}_{(k)}^{n}-\unicode[STIX]{x1D6FB}\cdot \widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}}_{(k)}^{n})=\widehat{\boldsymbol{g}}_{s}^{n} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{s},\end{eqnarray}$$
(4.56b )
$$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x1D70C}_{s}\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D6E5}t^{2}}\widehat{\boldsymbol{d}}_{(k)}^{n}-\unicode[STIX]{x1D6FB}\cdot \widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}}_{(k)}^{n})=\widehat{\boldsymbol{g}}_{s}^{n} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{s},\end{eqnarray}$$
(4.56b ) $$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x1D70E}_{s}\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\widehat{\boldsymbol{d}}_{(k)}^{n}+\widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}}_{(k)}^{n})\widehat{\boldsymbol{n}} & & \displaystyle \nonumber\\ \displaystyle \displaystyle \qquad =\unicode[STIX]{x1D70E}_{s}\widehat{\boldsymbol{v}}_{(k)}^{n}+\widehat{\boldsymbol{T}}_{f}(\widehat{\boldsymbol{v}}_{(k)}^{n},\widehat{p}_{(k)}^{n})\widehat{\boldsymbol{n}}-\unicode[STIX]{x1D70E}_{s}\widehat{\boldsymbol{g}}_{fs}^{n} & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x1D70E}_{s}\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\widehat{\boldsymbol{d}}_{(k)}^{n}+\widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}}_{(k)}^{n})\widehat{\boldsymbol{n}} & & \displaystyle \nonumber\\ \displaystyle \displaystyle \qquad =\unicode[STIX]{x1D70E}_{s}\widehat{\boldsymbol{v}}_{(k)}^{n}+\widehat{\boldsymbol{T}}_{f}(\widehat{\boldsymbol{v}}_{(k)}^{n},\widehat{p}_{(k)}^{n})\widehat{\boldsymbol{n}}-\unicode[STIX]{x1D70E}_{s}\widehat{\boldsymbol{g}}_{fs}^{n} & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4}.\end{eqnarray}$$
As proved in Causin et al. (Reference Causin, Gerbeau and Nobile2005), a small relaxation parameter is needed to achieve convergence in the implicit Dirichlet–Neumann scheme (corresponding to setting
 $\unicode[STIX]{x1D70E}_{f}=+\infty$
,
$\unicode[STIX]{x1D70E}_{f}=+\infty$
,
![]() $\unicode[STIX]{x1D70E}_{s}=0$
in (4.55c
, 4.56b
)). In practice, an Aitken relaxation procedure is often used to dynamically estimate an efficient relaxation parameter (Deparis Reference Deparis2004, Kuttler and Wall Reference Kuttler and Wall2008). A better situation is obtained by properly selecting the parameters in the Robin interface conditions (4.55c
, 4.56b
). In particular, the choice
$\unicode[STIX]{x1D70E}_{s}=0$
in (4.55c
, 4.56b
)). In practice, an Aitken relaxation procedure is often used to dynamically estimate an efficient relaxation parameter (Deparis Reference Deparis2004, Kuttler and Wall Reference Kuttler and Wall2008). A better situation is obtained by properly selecting the parameters in the Robin interface conditions (4.55c
, 4.56b
). In particular, the choice
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}_{f}=\displaystyle \frac{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D70C}_{s}H_{s}}{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6E5}t}+\displaystyle \frac{EH_{s}\unicode[STIX]{x1D6E5}t}{(1-\unicode[STIX]{x1D708}^{2})R^{2}},\,\unicode[STIX]{x1D70E}_{s}=0\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}_{f}=\displaystyle \frac{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D70C}_{s}H_{s}}{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6E5}t}+\displaystyle \frac{EH_{s}\unicode[STIX]{x1D6E5}t}{(1-\unicode[STIX]{x1D708}^{2})R^{2}},\,\unicode[STIX]{x1D70E}_{s}=0\end{eqnarray}$$
(where, as usual,
![]() $E$
and
$E$
and
![]() $\unicode[STIX]{x1D708}$
are Young’s modulus and the Poisson ratio for the vessel material at small deformations, and
$\unicode[STIX]{x1D708}$
are Young’s modulus and the Poisson ratio for the vessel material at small deformations, and
![]() $H_{s}$
and
$H_{s}$
and
![]() $R$
are the representative thickness and radius of the vessel) yields fast convergence without any relaxation (Robin–Neumann scheme: Badia, Nobile and Vergara Reference Badia, Nobile and Vergara2008a
, Nobile, Pozzoli and Vergara Reference Nobile, Pozzoli and Vergara2013). Gerardo-Giorda, Nobile and Vergara (Reference Gerardo-Giorda, Nobile and Vergara2010) and Gigante and Vergara (Reference Gigante and Vergara2015) have characterized the optimal value of
$R$
are the representative thickness and radius of the vessel) yields fast convergence without any relaxation (Robin–Neumann scheme: Badia, Nobile and Vergara Reference Badia, Nobile and Vergara2008a
, Nobile, Pozzoli and Vergara Reference Nobile, Pozzoli and Vergara2013). Gerardo-Giorda, Nobile and Vergara (Reference Gerardo-Giorda, Nobile and Vergara2010) and Gigante and Vergara (Reference Gigante and Vergara2015) have characterized the optimal value of
![]() $\unicode[STIX]{x1D70E}_{s}$
, leading to further improvement in the convergence history. Yu, Baek and Karniadakis (Reference Yu, Baek and Karniadakis2013) have derived a Dirichlet–Robin scheme by means of a generalized fictitious method, where the coefficients of the fluid pressure and vessel wall acceleration are changed to account for the added mass effect. This again allows one to obtain good convergence properties for haemodynamic parameters without any relaxation. Another class of implicit methods with good convergence properties for high added mass effect is based on adding a suitable interface artificial compressibility (IAC) consistent term to the fluid problem, proportional to the jump of pressure between two successive iterations (Degroote et al.
Reference Degroote, Swillens, Bruggeman, Segers and Vierendeels2010). Degroote (Reference Degroote2011) showed that for a finite volume approximation, the IAC method based on Dirichlet–Neumann iterations is equivalent to a Robin–Neumann scheme for a suitable choice of the parameter
$\unicode[STIX]{x1D70E}_{s}$
, leading to further improvement in the convergence history. Yu, Baek and Karniadakis (Reference Yu, Baek and Karniadakis2013) have derived a Dirichlet–Robin scheme by means of a generalized fictitious method, where the coefficients of the fluid pressure and vessel wall acceleration are changed to account for the added mass effect. This again allows one to obtain good convergence properties for haemodynamic parameters without any relaxation. Another class of implicit methods with good convergence properties for high added mass effect is based on adding a suitable interface artificial compressibility (IAC) consistent term to the fluid problem, proportional to the jump of pressure between two successive iterations (Degroote et al.
Reference Degroote, Swillens, Bruggeman, Segers and Vierendeels2010). Degroote (Reference Degroote2011) showed that for a finite volume approximation, the IAC method based on Dirichlet–Neumann iterations is equivalent to a Robin–Neumann scheme for a suitable choice of the parameter
![]() $\unicode[STIX]{x1D70E}_{f}$
.
$\unicode[STIX]{x1D70E}_{f}$
.
Partitioned algorithms for the FSI problem with a membrane structure.
Recently, several papers have analysed algorithms for FSI problems featuring a reduced membrane model for the vessel wall. In this case, the FSI problem is given by the fluid problem (4.19a
), the kinematic continuity condition (4.23a
) and the membrane equation (4.23b
), which in this case also plays the role of dynamic continuity condition. Moreover, homogeneous Dirichlet or Neumann conditions in the tangential direction need to be prescribed for the fluid problem at the interface
![]() $\unicode[STIX]{x1D6F4}$
. By considering an implicit time discretization of (4.23b
) and an explicit treatment of the geometry coupling, we obtain at each time step the following linearized FSI problem:
$\unicode[STIX]{x1D6F4}$
. By considering an implicit time discretization of (4.23b
) and an explicit treatment of the geometry coupling, we obtain at each time step the following linearized FSI problem:
 $$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x1D70C}_{f}\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\boldsymbol{v}^{n}+\unicode[STIX]{x1D70C}_{f}((\boldsymbol{v}^{\ast }-\boldsymbol{v}_{f}^{\ast })\cdot \unicode[STIX]{x1D6FB})\boldsymbol{v}^{n}-\unicode[STIX]{x1D6FB}\cdot \boldsymbol{T}_{f}(\boldsymbol{v}^{n},p^{n})=\boldsymbol{g}_{f}^{n} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f}^{\ast },\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x1D70C}_{f}\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\boldsymbol{v}^{n}+\unicode[STIX]{x1D70C}_{f}((\boldsymbol{v}^{\ast }-\boldsymbol{v}_{f}^{\ast })\cdot \unicode[STIX]{x1D6FB})\boldsymbol{v}^{n}-\unicode[STIX]{x1D6FB}\cdot \boldsymbol{T}_{f}(\boldsymbol{v}^{n},p^{n})=\boldsymbol{g}_{f}^{n} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f}^{\ast },\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D6FB}\cdot \boldsymbol{v}^{n}=0 & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f}^{\ast },\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D6FB}\cdot \boldsymbol{v}^{n}=0 & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f}^{\ast },\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{v}^{n}\cdot \boldsymbol{n}^{\ast }=\frac{\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}{d_{r}}^{n}+g_{fs}^{n} & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{\ast },\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{v}^{n}\cdot \boldsymbol{n}^{\ast }=\frac{\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}{d_{r}}^{n}+g_{fs}^{n} & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{\ast },\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{v}^{n}-(\boldsymbol{v}^{n}\cdot \boldsymbol{n}^{\ast })\boldsymbol{n}^{\ast }=\mathbf{0} & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{\ast },\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{v}^{n}-(\boldsymbol{v}^{n}\cdot \boldsymbol{n}^{\ast })\boldsymbol{n}^{\ast }=\mathbf{0} & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{\ast },\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x1D70C}_{s}H_{s}\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D6E5}t^{2}}d_{r}^{n}-\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{P}\unicode[STIX]{x1D6FB}d_{r}^{n})+\unicode[STIX]{x1D712}H_{s}d_{r}^{n} & & \displaystyle \nonumber\\ \displaystyle \qquad =-\boldsymbol{T}_{f}(\boldsymbol{v}^{n},p^{n})\boldsymbol{n}^{\ast }\cdot \boldsymbol{n}^{\ast }+g_{s}^{n} & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{\ast },\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x1D70C}_{s}H_{s}\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D6E5}t^{2}}d_{r}^{n}-\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{P}\unicode[STIX]{x1D6FB}d_{r}^{n})+\unicode[STIX]{x1D712}H_{s}d_{r}^{n} & & \displaystyle \nonumber\\ \displaystyle \qquad =-\boldsymbol{T}_{f}(\boldsymbol{v}^{n},p^{n})\boldsymbol{n}^{\ast }\cdot \boldsymbol{n}^{\ast }+g_{s}^{n} & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{\ast },\end{eqnarray}$$
The explicit Dirichlet–Neumann scheme applied to the previous monolithic problem reads as follows.
Explicit Dirichlet–Neumann scheme for the FSI problem with membrane structure
Given the quantities at previous time steps, at time step
![]() $t^{n}$
:
$t^{n}$
:
-
(1) Solve the Oseen problem with a Dirichlet condition at the FS interface:
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}ll@{}}\displaystyle \frac{\unicode[STIX]{x1D70C}_{f}\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\boldsymbol{v}^{n}+\unicode[STIX]{x1D70C}_{f}((\boldsymbol{v}^{\ast }-\boldsymbol{v}_{f}^{\ast })\cdot \unicode[STIX]{x1D6FB})\boldsymbol{v}^{n}-\unicode[STIX]{x1D6FB}\cdot \boldsymbol{T}_{f}(\boldsymbol{v}^{n},p^{n})=\boldsymbol{g}_{f}^{n} & \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f}^{\ast },\\ \displaystyle \unicode[STIX]{x1D6FB}\cdot \boldsymbol{v}^{n}=0 & \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f}^{\ast },\\ \displaystyle \boldsymbol{v}^{n}\cdot \boldsymbol{n}^{\ast }=\frac{\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}d_{r}^{n-1}+g_{fs}^{n-1} & \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{\ast },\\ \displaystyle \boldsymbol{v}^{n}-(\boldsymbol{v}^{n}\cdot \boldsymbol{n}^{\ast })\boldsymbol{n}^{\ast }=\mathbf{0} & \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{\ast }.\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}ll@{}}\displaystyle \frac{\unicode[STIX]{x1D70C}_{f}\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\boldsymbol{v}^{n}+\unicode[STIX]{x1D70C}_{f}((\boldsymbol{v}^{\ast }-\boldsymbol{v}_{f}^{\ast })\cdot \unicode[STIX]{x1D6FB})\boldsymbol{v}^{n}-\unicode[STIX]{x1D6FB}\cdot \boldsymbol{T}_{f}(\boldsymbol{v}^{n},p^{n})=\boldsymbol{g}_{f}^{n} & \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f}^{\ast },\\ \displaystyle \unicode[STIX]{x1D6FB}\cdot \boldsymbol{v}^{n}=0 & \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f}^{\ast },\\ \displaystyle \boldsymbol{v}^{n}\cdot \boldsymbol{n}^{\ast }=\frac{\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}d_{r}^{n-1}+g_{fs}^{n-1} & \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{\ast },\\ \displaystyle \boldsymbol{v}^{n}-(\boldsymbol{v}^{n}\cdot \boldsymbol{n}^{\ast })\boldsymbol{n}^{\ast }=\mathbf{0} & \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{\ast }.\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
-
(2) Then, solve the membrane problem:
 $$\begin{eqnarray}\frac{\unicode[STIX]{x1D70C}_{s}H_{s}\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D6E5}t^{2}}\widehat{d}_{r}^{n}-\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{P}\unicode[STIX]{x1D6FB}\widehat{d}_{r}^{n})+\unicode[STIX]{x1D712}H_{s}\widehat{d}_{r}^{n}=-\widehat{\boldsymbol{T}}_{f}(\widehat{\boldsymbol{v}}^{n},\widehat{p}^{n})\widehat{\boldsymbol{n}}\cdot \widehat{\boldsymbol{n}}+\widehat{g}_{s}^{n}\quad \text{on }\unicode[STIX]{x1D6F4}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D70C}_{s}H_{s}\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D6E5}t^{2}}\widehat{d}_{r}^{n}-\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{P}\unicode[STIX]{x1D6FB}\widehat{d}_{r}^{n})+\unicode[STIX]{x1D712}H_{s}\widehat{d}_{r}^{n}=-\widehat{\boldsymbol{T}}_{f}(\widehat{\boldsymbol{v}}^{n},\widehat{p}^{n})\widehat{\boldsymbol{n}}\cdot \widehat{\boldsymbol{n}}+\widehat{g}_{s}^{n}\quad \text{on }\unicode[STIX]{x1D6F4}.\end{eqnarray}$$
As in the case of scheme (4.47, 4.48), unfortunately this scheme is unconditionally absolutely unstable in the haemodynamic regime (Causin et al. Reference Causin, Gerbeau and Nobile2005).
Different algorithms are obtained by linearly combining the interface conditions (4.57c ) and (4.57e ) and by substituting the new condition in (4.57c ). In this case, we have to solve a coupled problem consisting of the following.
Robin–Neumann coupling for the FSI problem with membrane structure
Given the quantities at previous time steps, at time step
![]() $t^{n}$
:
$t^{n}$
:
-
(1) Solve the Oseen problem with a Robin condition at the FS interface:
(4.59a ) $$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x1D70C}_{f}\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\boldsymbol{v}^{n}+\unicode[STIX]{x1D70C}_{f}((\boldsymbol{v}^{\ast }-\boldsymbol{v}_{f}^{\ast })\cdot \unicode[STIX]{x1D6FB})\boldsymbol{v}^{n}-\unicode[STIX]{x1D6FB}\cdot \boldsymbol{T}_{f}(\boldsymbol{v}^{n},p^{n})=\boldsymbol{g}_{f}^{n} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f}^{\ast },\end{eqnarray}$$
(4.59b )
$$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x1D70C}_{f}\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}\boldsymbol{v}^{n}+\unicode[STIX]{x1D70C}_{f}((\boldsymbol{v}^{\ast }-\boldsymbol{v}_{f}^{\ast })\cdot \unicode[STIX]{x1D6FB})\boldsymbol{v}^{n}-\unicode[STIX]{x1D6FB}\cdot \boldsymbol{T}_{f}(\boldsymbol{v}^{n},p^{n})=\boldsymbol{g}_{f}^{n} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f}^{\ast },\end{eqnarray}$$
(4.59b ) $$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D6FB}\cdot \boldsymbol{v}^{n}=0 & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f}^{\ast },\end{eqnarray}$$
(4.59c )
$$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D6FB}\cdot \boldsymbol{v}^{n}=0 & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{f}^{\ast },\end{eqnarray}$$
(4.59c ) $$\begin{eqnarray}\displaystyle \displaystyle (\unicode[STIX]{x1D70E}_{f}\boldsymbol{v}^{n}+\boldsymbol{T}_{f}(\boldsymbol{v}^{n},p^{n})\boldsymbol{n}^{\ast })\cdot \boldsymbol{n}^{\ast }\unicode[STIX]{x1D70E}_{f}\biggl(\frac{\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}d_{r}^{n}+g_{fs}^{n}\biggr) & & \displaystyle \nonumber\\ \displaystyle \qquad -\,\biggl(\frac{\unicode[STIX]{x1D70C}_{s}H_{s}\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D6E5}t^{2}}d_{r}^{n}-\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{P}\unicode[STIX]{x1D6FB}d_{r}^{n})+\unicode[STIX]{x1D712}H_{s}d_{r}^{n}\biggr) & \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{\ast }, & \displaystyle\end{eqnarray}$$
(4.59d )
$$\begin{eqnarray}\displaystyle \displaystyle (\unicode[STIX]{x1D70E}_{f}\boldsymbol{v}^{n}+\boldsymbol{T}_{f}(\boldsymbol{v}^{n},p^{n})\boldsymbol{n}^{\ast })\cdot \boldsymbol{n}^{\ast }\unicode[STIX]{x1D70E}_{f}\biggl(\frac{\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6E5}t}d_{r}^{n}+g_{fs}^{n}\biggr) & & \displaystyle \nonumber\\ \displaystyle \qquad -\,\biggl(\frac{\unicode[STIX]{x1D70C}_{s}H_{s}\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D6E5}t^{2}}d_{r}^{n}-\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{P}\unicode[STIX]{x1D6FB}d_{r}^{n})+\unicode[STIX]{x1D712}H_{s}d_{r}^{n}\biggr) & \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{\ast }, & \displaystyle\end{eqnarray}$$
(4.59d ) $$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{v}^{n}-(\boldsymbol{v}^{n}\cdot \boldsymbol{n}^{\ast })\boldsymbol{n}^{\ast }=\mathbf{0} & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{\ast }.\!\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{v}^{n}-(\boldsymbol{v}^{n}\cdot \boldsymbol{n}^{\ast })\boldsymbol{n}^{\ast }=\mathbf{0} & & \displaystyle \displaystyle \text{on }\unicode[STIX]{x1D6F4}^{\ast }.\!\end{eqnarray}$$
-
(2) Solve the membrane problem:
(4.60) $$\begin{eqnarray}\frac{\unicode[STIX]{x1D70C}_{s}H_{s}\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D6E5}t^{2}}\widehat{d}_{r}^{n}-\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{P}\unicode[STIX]{x1D6FB}\widehat{d}_{r}^{n})+\unicode[STIX]{x1D712}H_{s}\widehat{d}_{r}^{n}=-\widehat{\boldsymbol{T}}_{f}(\widehat{\boldsymbol{v}}^{n},\widehat{p}^{n})\widehat{\boldsymbol{n}}\cdot \widehat{\boldsymbol{n}}+\widehat{g}_{s}^{n}\quad \text{on }\unicode[STIX]{x1D6F4}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D70C}_{s}H_{s}\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D6E5}t^{2}}\widehat{d}_{r}^{n}-\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{P}\unicode[STIX]{x1D6FB}\widehat{d}_{r}^{n})+\unicode[STIX]{x1D712}H_{s}\widehat{d}_{r}^{n}=-\widehat{\boldsymbol{T}}_{f}(\widehat{\boldsymbol{v}}^{n},\widehat{p}^{n})\widehat{\boldsymbol{n}}\cdot \widehat{\boldsymbol{n}}+\widehat{g}_{s}^{n}\quad \text{on }\unicode[STIX]{x1D6F4}.\end{eqnarray}$$
The above problem could be solved either monolithically or by means of a block Gauss–Seidel method that in fact introduces sub-iterations splitting the solution of (4.59) and (4.60). When
![]() $\boldsymbol{P}=\mathbf{0}$
, the special choice
$\boldsymbol{P}=\mathbf{0}$
, the special choice
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}_{f}=\widetilde{\unicode[STIX]{x1D70E}}_{f}=\frac{\unicode[STIX]{x1D70C}_{s}H_{s}\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6E5}t}+\frac{\unicode[STIX]{x1D712}H_{s}\unicode[STIX]{x1D6E5}t}{\unicode[STIX]{x1D6FC}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}_{f}=\widetilde{\unicode[STIX]{x1D70E}}_{f}=\frac{\unicode[STIX]{x1D70C}_{s}H_{s}\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6E5}t}+\frac{\unicode[STIX]{x1D712}H_{s}\unicode[STIX]{x1D6E5}t}{\unicode[STIX]{x1D6FC}},\end{eqnarray}$$
introduced in (4.59c ), yields
 $$\begin{eqnarray}(\widetilde{\unicode[STIX]{x1D70E}}_{f}\boldsymbol{v}^{n}+\boldsymbol{T}_{f}(\boldsymbol{v}^{n},p^{n})\boldsymbol{n}^{\ast })\cdot \boldsymbol{n}^{\ast }=\widetilde{\unicode[STIX]{x1D70E}}_{f}g_{fs}^{n}\quad \text{on }\unicode[STIX]{x1D6F4}^{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}(\widetilde{\unicode[STIX]{x1D70E}}_{f}\boldsymbol{v}^{n}+\boldsymbol{T}_{f}(\boldsymbol{v}^{n},p^{n})\boldsymbol{n}^{\ast })\cdot \boldsymbol{n}^{\ast }=\widetilde{\unicode[STIX]{x1D70E}}_{f}g_{fs}^{n}\quad \text{on }\unicode[STIX]{x1D6F4}^{\ast }.\end{eqnarray}$$
At this stage, this is a Robin condition for the fluid problem without any explicit dependence on
![]() $d_{r}^{n}$
. Thus, the monolithic problem given by (4.59, 4.60, 4.61) is equivalent to the stand-alone fluid problem (4.59a
, 4.59b
, 4.59d
, 4.62): see Nobile and Vergara (Reference Nobile and Vergara2008). The solution of this fluid problem can then be used to feed the right-hand side of (4.60) and to get the structure displacement
$d_{r}^{n}$
. Thus, the monolithic problem given by (4.59, 4.60, 4.61) is equivalent to the stand-alone fluid problem (4.59a
, 4.59b
, 4.59d
, 4.62): see Nobile and Vergara (Reference Nobile and Vergara2008). The solution of this fluid problem can then be used to feed the right-hand side of (4.60) and to get the structure displacement
![]() $\widehat{d}_{r}^{n}$
. In this way, the fluid and structure problems are in fact decoupled, even if the coupling conditions are treated implicitly. This provides a smart and efficient way to solve the monolithic problem (4.57) exactly, at the expense of a single fluid problem solve (note that the membrane problem (4.60) is solved very cheaply).
$\widehat{d}_{r}^{n}$
. In this way, the fluid and structure problems are in fact decoupled, even if the coupling conditions are treated implicitly. This provides a smart and efficient way to solve the monolithic problem (4.57) exactly, at the expense of a single fluid problem solve (note that the membrane problem (4.60) is solved very cheaply).
Starting from this result, Guidoboni et al. (Reference Guidoboni, Glowinski, Cavallini and Canic2009) have proposed a stable Robin–Neumann scheme based on an operator splitting, for a general membrane law (
![]() $\boldsymbol{P}\neq \mathbf{0}$
). The inertial vessel wall term is treated implicitly as in the previous case, leading to a Robin boundary condition for the fluid with
$\boldsymbol{P}\neq \mathbf{0}$
). The inertial vessel wall term is treated implicitly as in the previous case, leading to a Robin boundary condition for the fluid with
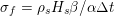 $\unicode[STIX]{x1D70E}_{f}=\unicode[STIX]{x1D70C}_{s}H_{s}\unicode[STIX]{x1D6FD}/\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6E5}t$
, whereas the elastic and algebraic contributions are treated explicitly. Fernández (Reference Fernández2013) proposes an incremental version of this scheme, where the elastic and algebraic parts of the membrane law are included in the Robin condition for the fluid problem by means of a suitable extrapolation from previous time steps. Finally, we mention Colciago et al. (Reference Colciago, Deparis and Quarteroni2014), who treat the whole membrane law implicitly, leading to a generalized Robin condition, which however requires an ad hoc implementation.
$\unicode[STIX]{x1D70E}_{f}=\unicode[STIX]{x1D70C}_{s}H_{s}\unicode[STIX]{x1D6FD}/\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6E5}t$
, whereas the elastic and algebraic contributions are treated explicitly. Fernández (Reference Fernández2013) proposes an incremental version of this scheme, where the elastic and algebraic parts of the membrane law are included in the Robin condition for the fluid problem by means of a suitable extrapolation from previous time steps. Finally, we mention Colciago et al. (Reference Colciago, Deparis and Quarteroni2014), who treat the whole membrane law implicitly, leading to a generalized Robin condition, which however requires an ad hoc implementation.
Partitioned algorithms based on the Schur complement.
Here we discuss partitioned schemes arising from an interface equation written for the FSI problem and introduced by Deparis et al. (Reference Deparis, Discacciati, Fourestey and Quarteroni2006). For the sake of exposition, we introduce the algebraic counterpart of (4.45) related to a finite element discretization for the case of linear elasticity for the vessel wall problem:

where the superscript
![]() $f$
refers to internal fluid variables,
$f$
refers to internal fluid variables,
![]() $s$
to internal variables for the vessel wall,
$s$
to internal variables for the vessel wall,
![]() $\unicode[STIX]{x1D6F4}$
to the FS interface variables;
$\unicode[STIX]{x1D6F4}$
to the FS interface variables;
![]() $C$
(with superscripts) refers to fluid matrices,
$C$
(with superscripts) refers to fluid matrices,
![]() $G$
to vessel wall matrices,
$G$
to vessel wall matrices,
![]() $M^{\unicode[STIX]{x1D6F4}}$
is the FS interface mass matrix;
$M^{\unicode[STIX]{x1D6F4}}$
is the FS interface mass matrix;
![]() $\boldsymbol{V}$
includes the fluid and pressure variables,
$\boldsymbol{V}$
includes the fluid and pressure variables,
![]() $\boldsymbol{D}^{s}$
the vessel wall displacement internal variables, and
$\boldsymbol{D}^{s}$
the vessel wall displacement internal variables, and
![]() $\boldsymbol{U}^{\unicode[STIX]{x1D6F4}}$
the vessel wall velocity interface variables; the vectors
$\boldsymbol{U}^{\unicode[STIX]{x1D6F4}}$
the vessel wall velocity interface variables; the vectors
![]() $\boldsymbol{b}$
denote the right-hand sides. The first row corresponds to the momentum and mass conservation for the fluid, the second and third rows to the interface kinematic and dynamic conditions, and the last row to the vessel wall problem. By eliminating
$\boldsymbol{b}$
denote the right-hand sides. The first row corresponds to the momentum and mass conservation for the fluid, the second and third rows to the interface kinematic and dynamic conditions, and the last row to the vessel wall problem. By eliminating
 $\boldsymbol{V}^{f},\,\boldsymbol{V}^{\unicode[STIX]{x1D6F4}}$
and
$\boldsymbol{V}^{f},\,\boldsymbol{V}^{\unicode[STIX]{x1D6F4}}$
and
![]() $\boldsymbol{D}^{s}$
from (4.63), we obtain the interface equation
$\boldsymbol{D}^{s}$
from (4.63), we obtain the interface equation
 $$\begin{eqnarray}(\widetilde{C}^{\unicode[STIX]{x1D6F4}}+\widetilde{G}^{\unicode[STIX]{x1D6F4}})\boldsymbol{U}^{\unicode[STIX]{x1D6F4}}=\widetilde{\mathbf{b}}^{\unicode[STIX]{x1D6F4}},\end{eqnarray}$$
$$\begin{eqnarray}(\widetilde{C}^{\unicode[STIX]{x1D6F4}}+\widetilde{G}^{\unicode[STIX]{x1D6F4}})\boldsymbol{U}^{\unicode[STIX]{x1D6F4}}=\widetilde{\mathbf{b}}^{\unicode[STIX]{x1D6F4}},\end{eqnarray}$$
where
 $$\begin{eqnarray}\widetilde{C}^{\unicode[STIX]{x1D6F4}}=C^{\unicode[STIX]{x1D6F4}\unicode[STIX]{x1D6F4}}-C^{\unicode[STIX]{x1D6F4}f}(C^{ff})^{-1}C^{f\unicode[STIX]{x1D6F4}}\quad \text{and}\quad \widetilde{G}^{\unicode[STIX]{x1D6F4}}=G^{\unicode[STIX]{x1D6F4}\unicode[STIX]{x1D6F4}}-G^{\unicode[STIX]{x1D6F4}s}(G^{ss})^{-1}G^{s\unicode[STIX]{x1D6F4}}\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{C}^{\unicode[STIX]{x1D6F4}}=C^{\unicode[STIX]{x1D6F4}\unicode[STIX]{x1D6F4}}-C^{\unicode[STIX]{x1D6F4}f}(C^{ff})^{-1}C^{f\unicode[STIX]{x1D6F4}}\quad \text{and}\quad \widetilde{G}^{\unicode[STIX]{x1D6F4}}=G^{\unicode[STIX]{x1D6F4}\unicode[STIX]{x1D6F4}}-G^{\unicode[STIX]{x1D6F4}s}(G^{ss})^{-1}G^{s\unicode[STIX]{x1D6F4}}\end{eqnarray}$$
are the fluid and vessel wall Schur complement matrices and
 $$\begin{eqnarray}\widetilde{\mathbf{b}}^{\unicode[STIX]{x1D6F4}}=\mathbf{b}^{\unicode[STIX]{x1D6F4}}-C^{\unicode[STIX]{x1D6F4}f}(C^{ff})^{-1}\mathbf{b}^{f}-G^{\unicode[STIX]{x1D6F4}s}(G^{ss})^{-1}\mathbf{b}^{s}\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{\mathbf{b}}^{\unicode[STIX]{x1D6F4}}=\mathbf{b}^{\unicode[STIX]{x1D6F4}}-C^{\unicode[STIX]{x1D6F4}f}(C^{ff})^{-1}\mathbf{b}^{f}-G^{\unicode[STIX]{x1D6F4}s}(G^{ss})^{-1}\mathbf{b}^{s}\end{eqnarray}$$
is the corresponding right-hand side.
The Robin–Robin method (4.55, 4.56) could be obtained by applying the Richardson method to the interface equation (4.64) preconditioned by the matrix
 $$\begin{eqnarray}P=\frac{1}{\unicode[STIX]{x1D70E}_{f}+\unicode[STIX]{x1D70E}_{s}}(\widetilde{C}^{\unicode[STIX]{x1D6F4}}+\unicode[STIX]{x1D70E}_{f}M^{\unicode[STIX]{x1D6F4}})(M^{\unicode[STIX]{x1D6F4}})^{-1}(\widetilde{G}^{\unicode[STIX]{x1D6F4}}+\unicode[STIX]{x1D70E}_{s}M^{\unicode[STIX]{x1D6F4}}).\end{eqnarray}$$
$$\begin{eqnarray}P=\frac{1}{\unicode[STIX]{x1D70E}_{f}+\unicode[STIX]{x1D70E}_{s}}(\widetilde{C}^{\unicode[STIX]{x1D6F4}}+\unicode[STIX]{x1D70E}_{f}M^{\unicode[STIX]{x1D6F4}})(M^{\unicode[STIX]{x1D6F4}})^{-1}(\widetilde{G}^{\unicode[STIX]{x1D6F4}}+\unicode[STIX]{x1D70E}_{s}M^{\unicode[STIX]{x1D6F4}}).\end{eqnarray}$$
This leads to a new family of partitioned schemes obtained by applying other Krylov methods to (4.64) with the same preconditioner. For example, GMRES preconditioned by the Dirichlet–Neumann preconditioner
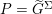 $P=\widetilde{G}^{\unicode[STIX]{x1D6F4}}$
is considered in Badia, Quaini and Quarteroni (Reference Badia, Quaini and Quarteroni2008b
), whereas GMRES preconditioned with the RR preconditioner (4.65) is introduced in Badia, Nobile and Vergara (Reference Badia, Nobile and Vergara2009). The first of these two schemes highlighted better convergence properties with respect to the classical Dirichlet–Neumann method, whereas the second is more robust with respect to the choice of the interface parameters
$P=\widetilde{G}^{\unicode[STIX]{x1D6F4}}$
is considered in Badia, Quaini and Quarteroni (Reference Badia, Quaini and Quarteroni2008b
), whereas GMRES preconditioned with the RR preconditioner (4.65) is introduced in Badia, Nobile and Vergara (Reference Badia, Nobile and Vergara2009). The first of these two schemes highlighted better convergence properties with respect to the classical Dirichlet–Neumann method, whereas the second is more robust with respect to the choice of the interface parameters
![]() $\unicode[STIX]{x1D70E}_{f},\,\unicode[STIX]{x1D70E}_{s}$
than the classical Robin–Robin method.
$\unicode[STIX]{x1D70E}_{f},\,\unicode[STIX]{x1D70E}_{s}$
than the classical Robin–Robin method.
In some works, a non-linear interface equation is written directly for the non-linear problem (4.44) and a Newton method is then applied to this equation (Fernández and Moubachir Reference Fernández and Moubachir2005, Degroote and Vierendeels Reference Degroote and Vierendeels2011).
Remark 4.2. In the partitioned schemes introduced above, the vessel wall subproblem appearing at each iteration is still non-linear, that is, we have not discussed how to tackle point (iii) in the list of issues reported at the beginning of the subsection. The simplest way to treat vessel wall non-linearity – very appropriate when a non-linear structural solver is available – is to introduce inner Newton sub-iterations at each Robin–Robin iteration. Alternatively, Kuttler et al. (Reference Kuttler, Gee, Forster, Comerford and Wall2010) have proposed a scheme based on integrating the management of the five sources of non-linearities/coupling (geometric coupling and adherence, fluid and structure constitutive non-linearities, physical coupling) in a single inexact-Newton loop. Other possible combinations will be discussed later on as specific monolithic procedures. For a detailed overview with numerical comparisons we refer to Nobile et al. (Reference Nobile, Pozzoli and Vergara2014).
Monolithic solvers.
As an alternative to partitioned schemes, monolithic procedures have been successfully considered in haemodynamics for the solution of the FSI problem (4.45). These methods consist in applying an exact or inexact Newton method to the whole non-linear FSI problem. Referring to the notation introduced above, by considering a finite element space discretization and the inexact Newton method, we obtain from (4.45)
 $$\begin{eqnarray}\widetilde{J}(\boldsymbol{x}_{(k-1)})\unicode[STIX]{x1D6FF}\boldsymbol{x}_{(k)}=\boldsymbol{G}-\boldsymbol{{\mathcal{A}}}(\boldsymbol{x}_{(k-1)})\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{J}(\boldsymbol{x}_{(k-1)})\unicode[STIX]{x1D6FF}\boldsymbol{x}_{(k)}=\boldsymbol{G}-\boldsymbol{{\mathcal{A}}}(\boldsymbol{x}_{(k-1)})\end{eqnarray}$$
(for simplicity we omit the temporal index
![]() $n$
), where
$n$
), where
![]() $\widetilde{J}$
is the Jacobian matrix or a suitable approximation of it,
$\widetilde{J}$
is the Jacobian matrix or a suitable approximation of it,
 $\boldsymbol{x}=[\boldsymbol{V}^{f}\,\,\boldsymbol{V}^{\unicode[STIX]{x1D6F4}}\,\,\boldsymbol{U}^{\unicode[STIX]{x1D6F4}}\,\,\boldsymbol{D}^{s}]^{T}$
, and
$\boldsymbol{x}=[\boldsymbol{V}^{f}\,\,\boldsymbol{V}^{\unicode[STIX]{x1D6F4}}\,\,\boldsymbol{U}^{\unicode[STIX]{x1D6F4}}\,\,\boldsymbol{D}^{s}]^{T}$
, and
 $\boldsymbol{{\mathcal{A}}}(\boldsymbol{x})=\boldsymbol{G}$
is the non-linear system related to (4.45). The exact Jacobian matrix is given by
$\boldsymbol{{\mathcal{A}}}(\boldsymbol{x})=\boldsymbol{G}$
is the non-linear system related to (4.45). The exact Jacobian matrix is given by

where the submatrices
![]() $J_{G}$
are the exact Jacobians of
$J_{G}$
are the exact Jacobians of
![]() $\boldsymbol{{\mathcal{A}}}$
related to the structure variables. For the solution of the linear systems (4.66) with the exact Jacobian, classical strategies used so far for haemodynamics include GMRES preconditioned by a one-level additive Schwarz method (Barker and Cai Reference Barker and Cai2010a
) and global algebraic multigrid (Gee, Kuttler and Wall Reference Gee, Kuttler and Wall2011). Barker and Cai (Reference Barker and Cai2010b
) use a two-level Newton method in combination with a two-level hybrid Schwarz preconditioner, where the solution on a coarse grid is used to provide a good initial guess to the Newton method. Alternatively, inexact Newton methods have been considered, for example by means of block approximations
$\boldsymbol{{\mathcal{A}}}$
related to the structure variables. For the solution of the linear systems (4.66) with the exact Jacobian, classical strategies used so far for haemodynamics include GMRES preconditioned by a one-level additive Schwarz method (Barker and Cai Reference Barker and Cai2010a
) and global algebraic multigrid (Gee, Kuttler and Wall Reference Gee, Kuttler and Wall2011). Barker and Cai (Reference Barker and Cai2010b
) use a two-level Newton method in combination with a two-level hybrid Schwarz preconditioner, where the solution on a coarse grid is used to provide a good initial guess to the Newton method. Alternatively, inexact Newton methods have been considered, for example by means of block approximations
![]() $\widetilde{J}$
of
$\widetilde{J}$
of
![]() $J$
splitting the fluid velocity, pressure and vessel wall unknowns (Heil Reference Heil2004, Crosetto et al.
Reference Crosetto, Deparis, Fourestey and Quarteroni2011).
$J$
splitting the fluid velocity, pressure and vessel wall unknowns (Heil Reference Heil2004, Crosetto et al.
Reference Crosetto, Deparis, Fourestey and Quarteroni2011).
A particular class of inexact Newton methods is obtained by neglecting the term
![]() $-M_{\unicode[STIX]{x1D6F4}}$
appearing in the upper-right block of the exact Jacobian (4.67). This yields in fact a class of partitioned schemes of Dirichlet–Neumann type where issues (iii) and (v) (vessel wall non-linearity and physical coupling) are treated within the same iterations. An example is given by the preconditioner proposed in Crosetto et al. (Reference Crosetto, Deparis, Fourestey and Quarteroni2011), where the fluid and structure blocks in (4.67) are approximated by the corresponding algebraic additive Schwarz preconditioners. This method is strongly scalable for haemodynamic applications. Recently, Deparis et al. (Reference Deparis, Forti, Grandperrin and Quarteroni2016) have introduced a variant of the above preconditioner. This new preconditioner, named FaCSI, is based on operating a static condensation of the fluid interface variables and using a SIMPLE preconditioner for the fluid block.
$-M_{\unicode[STIX]{x1D6F4}}$
appearing in the upper-right block of the exact Jacobian (4.67). This yields in fact a class of partitioned schemes of Dirichlet–Neumann type where issues (iii) and (v) (vessel wall non-linearity and physical coupling) are treated within the same iterations. An example is given by the preconditioner proposed in Crosetto et al. (Reference Crosetto, Deparis, Fourestey and Quarteroni2011), where the fluid and structure blocks in (4.67) are approximated by the corresponding algebraic additive Schwarz preconditioners. This method is strongly scalable for haemodynamic applications. Recently, Deparis et al. (Reference Deparis, Forti, Grandperrin and Quarteroni2016) have introduced a variant of the above preconditioner. This new preconditioner, named FaCSI, is based on operating a static condensation of the fluid interface variables and using a SIMPLE preconditioner for the fluid block.
For the sake of exposition, we have discussed numerical strategies for the FSI problem based on finite elements for the space discretization and finite differences for the time discretization. Other strategies considered so far in haemodynamics are space-time finite elements (see e.g. Tezduyar et al. Reference Tezduyar, Sathe, Cragin, Nanna, Conklin, Pausewang and Schwaab2007, Bazilevs, Takizawa and Tezduyar Reference Bazilevs, Takizawa and Tezduyar2012) and the methods based on isogeometric analysis (see Bazilevs et al. Reference Bazilevs, Calo, Zhang and Hughes2006, Bazilevs et al. Reference Bazilevs, Gohean, Hughes, Moser and Zhang2009).
In Figure 4.7 we illustrate some examples of numerical results obtained in real geometries reconstructed from radiological images (see the caption for details).

Figure 4.7. (a) Blood velocity streamlines and vessel wall displacement vectors in a stenotic carotid artery (MRI images from the Vascular Surgery and Radiology Divisions at Ospedale Maggiore Policlinico, Milan, Italy). (b–d) Results of a FSI simulation in the ascending and thoracic aorta (MRI images from www.vascularmodel.com/sandbox/doku.php?id=repository). Blood velocity magnitude in the whole domain (b) and on a selected longitudinal section (c), vessel wall displacements (d). All cases refer to the systolic peak. Numerical results were obtained using LifeV, P1-Bubble/P1 finite elements for the fluid problem and P1 finite elements for the vessel wall problem; the backward Euler scheme and the midpoint method was used for the time discretization of the fluid and vessel wall problems, respectively. The implicit Robin–Robin partitioned scheme was used in case (a) and the FaCSI preconditioner in cases (b–d).
4.6.4 Numerical methods for defective boundary problems
For the numerical solution of the augmented formulation (4.27), one could rely either on a monolithic strategy, where the full augmented matrix is constructed and solved, or on splitting techniques. For the latter, Formaggia et al. (Reference Formaggia, Gerbeau, Nobile and Quarteroni2002) and Veneziani and Vergara (Reference Veneziani and Vergara2005) propose writing the Schur complement equation with respect to the Lagrange multiplier of the linearized and discretized (in time and space) augmented formulation. This is a linear system whose dimension is equal to the number of flow rate conditions, say
![]() $m\geq 1$
. By using the GMRES method to solve this system iteratively, the exact solution is reached after exactly
$m\geq 1$
. By using the GMRES method to solve this system iteratively, the exact solution is reached after exactly
![]() $m$
iterations (in exact arithmetic). At each iteration, the solution of a standard fluid problem with Neumann conditions is needed (exact splitting technique). The solution of a further standard fluid problem is required to compute the initial residual in the GMRES algorithm. This approach is quite expensive, even for the case
$m$
iterations (in exact arithmetic). At each iteration, the solution of a standard fluid problem with Neumann conditions is needed (exact splitting technique). The solution of a further standard fluid problem is required to compute the initial residual in the GMRES algorithm. This approach is quite expensive, even for the case
![]() $m=1$
, which requires the solution of two fluid problems per time step. However, it preserves modularity; indeed, it can be implemented using available standard fluid solvers in a black box mode. This is an interesting property when applications to cases of real interest are addressed: see Viscardi et al. (Reference Viscardi, Vergara, Antiga, Merelli, Veneziani, Puppini, Faggian, Mazzucco and Luciani2010), Vergara et al. (Reference Vergara, Viscardi, Antiga and Luciani2012), Piccinelli et al. (Reference Piccinelli, Vergara, Antiga, Forzenigo, Biondetti and Domanin2013) and Guerciotti et al. Reference Guerciotti, Vergara, Azzimonti, Forzenigo, Buora, Biondetti and Domanin2015, Reference Guerciotti, Vergara, Ippolito, Quarteroni, Antona and Scrofani2017.
$m=1$
, which requires the solution of two fluid problems per time step. However, it preserves modularity; indeed, it can be implemented using available standard fluid solvers in a black box mode. This is an interesting property when applications to cases of real interest are addressed: see Viscardi et al. (Reference Viscardi, Vergara, Antiga, Merelli, Veneziani, Puppini, Faggian, Mazzucco and Luciani2010), Vergara et al. (Reference Vergara, Viscardi, Antiga and Luciani2012), Piccinelli et al. (Reference Piccinelli, Vergara, Antiga, Forzenigo, Biondetti and Domanin2013) and Guerciotti et al. Reference Guerciotti, Vergara, Azzimonti, Forzenigo, Buora, Biondetti and Domanin2015, Reference Guerciotti, Vergara, Ippolito, Quarteroni, Antona and Scrofani2017.
To reduce the computational time required by the exact splitting approach, Veneziani and Vergara (Reference Veneziani and Vergara2007) propose a different (inexact) splitting procedure, requiring the solution of
![]() $m$
steady problems out of the temporal loop and of one unsteady null flow rate problem at each time step. This strategy introduces an error near the section which is smaller than the one based on conjecturing the velocity profile in the original (non-null) flow rate problem: see Section 4.4.1.
$m$
steady problems out of the temporal loop and of one unsteady null flow rate problem at each time step. This strategy introduces an error near the section which is smaller than the one based on conjecturing the velocity profile in the original (non-null) flow rate problem: see Section 4.4.1.
For the numerical solution of the control-based approach described in Section 4.4.3, Formaggia et al. Reference Formaggia, Veneziani and Vergara2008, Reference Formaggia, Veneziani and Vergara2009b have considered classical iterative methods for the solution of the resulting KKT system.
Recently, a numerical approach based on the Nitsche method has been considered to prescribe a flow rate condition. In particular, the original idea of prescribing Dirichlet conditions with a consistent penalization approach (Nitsche Reference Nitsche1970/71) has been extended by Zunino (Reference Zunino2009) to the case of flow rate boundary conditions. This strategy does not introduce further variables other than those of the original problem, but it does require careful tuning of a penalization parameter. In addition, it deals with non-standard bilinear forms that need ad hoc implementation. However, it should be very effective if flow rate conditions are implemented in a DG code. Vergara (Reference Vergara2011) has considered a similar approach to fulfilling the mean pressure condition (3.3) and the FSI case; see also Porpora et al. (Reference Porpora, Zunino, Vergara and Piccinelli2012).
For a more comprehensive overview of numerical strategies for defective boundary problems, we refer the reader to Formaggia and Vergara (Reference Formaggia and Vergara2012).
4.6.5 Numerical methods for the geometric reduced models and multiscale approach
For the numerical solution of the 1D reduced model (4.30), in principle any convenient approximation method for non-linear hyperbolic equations can be used. The peculiar feature of this model, however, is the lack of discontinuous solutions. A common approach relies on the finite element version of the Lax–Wendroff scheme, thanks to its excellent dispersion properties (Formaggia et al. Reference Formaggia, Gerbeau, Nobile and Quarteroni2001). As this scheme is explicit, a CFL-like condition is required to ensure absolute stability. In the presence of a viscoelastic term, the 1D model is usually discretized by means of a splitting procedure where the solution is split into two components, one satisfying the pure elastic problem and the other satisfying the viscoelastic correction (Formaggia et al. Reference Formaggia, Lamponi and Quarteroni2003, Malossi, Blanco and Deparis Reference Malossi, Blanco and Deparis2012). High-order methods are suitable for capturing the (physical) reflections at bifurcations induced by the vessel tapering: see e.g. Sherwin et al. (Reference Sherwin, Franke, Peiró and Parker2003b ) and Sherwin et al. (Reference Sherwin, Formaggia, Peiró and Franke2003a ) for a discontinuous Galerkin discretization and Muller and Toro (Reference Muller and Toro2014) for a finite volume scheme.
Regarding 0D models, they are in general described by systems of differential and algebraic equations, possibly non-linear due to the presence of diodes to represent the valves (Formaggia et al. Reference Formaggia, Quarteroni and Veneziani2009a ). Usually, for haemodynamic applications, these systems can be reduced to classical Cauchy problems and solved by classical Runge–Kutta methods.
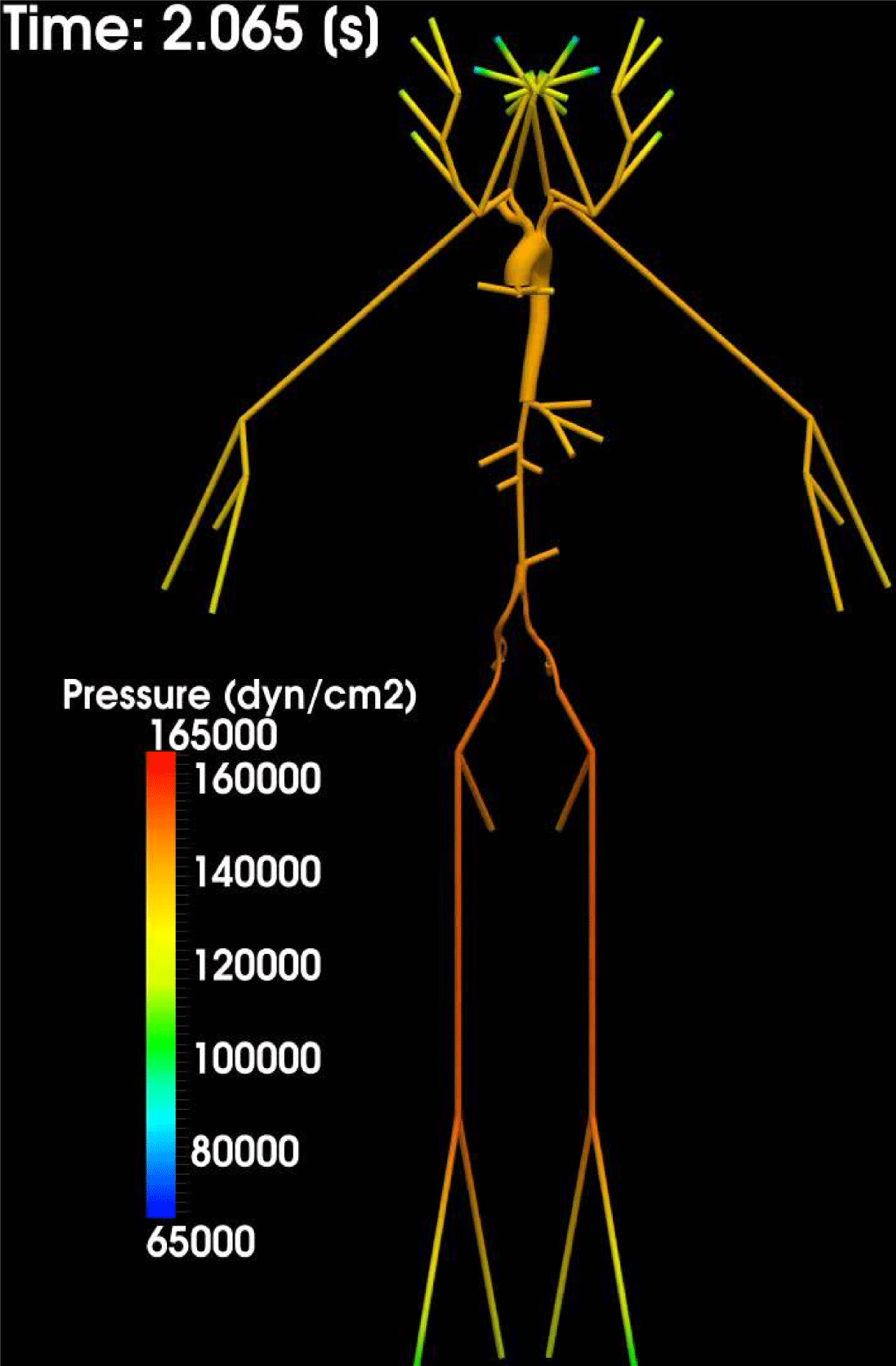
Figure 4.8. Pressure wave propagation in an ascending aorta (3D model) and in the 1D model of the systemic circulation. Numerical results were obtained using LifeV; the Newton method was used for the interface equation. Courtesy of C. Malossi.
As for the solution of the 3D/1D coupled problems described in Section 4.5.2, we can in principle identify three different strategies, namely partitioned schemes, monolithic approaches, and methods based on the solution of an interface equation. In partitioned schemes, the 3D and 1D problems are solved separately in an iterative framework. The coupling interface conditions can be enforced in many different ways. For example, we can prescribe the flow rate condition (4.39a
) to the 3D problem and the pressure condition (4.42) to the 1D problem. Different algorithms are obtained by switching the role of the interface conditions in the iterative algorithm or by considering other interface conditions (e.g. (4.39b
)). This is also the case when one of the two interface conditions is replaced by a condition expressing the continuity of the characteristic variable
![]() $W_{1}$
entering the 1D domain (Formaggia et al.
Reference Formaggia, Gerbeau, Nobile and Quarteroni2001, Papadakis Reference Papadakis2009), that is, according to (4.33),
$W_{1}$
entering the 1D domain (Formaggia et al.
Reference Formaggia, Gerbeau, Nobile and Quarteroni2001, Papadakis Reference Papadakis2009), that is, according to (4.33),
 $$\begin{eqnarray}W_{1}(t)|_{z=0}=\unicode[STIX]{x1D701}_{1}\biggl(|\unicode[STIX]{x1D6E4}_{f}^{t}|,\int _{\unicode[STIX]{x1D6E4}_{f}^{t}}\boldsymbol{v}\cdot \boldsymbol{n}\text{d}\unicode[STIX]{x1D6FE}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}W_{1}(t)|_{z=0}=\unicode[STIX]{x1D701}_{1}\biggl(|\unicode[STIX]{x1D6E4}_{f}^{t}|,\int _{\unicode[STIX]{x1D6E4}_{f}^{t}}\boldsymbol{v}\cdot \boldsymbol{n}\text{d}\unicode[STIX]{x1D6FE}\biggr).\end{eqnarray}$$
In any case, each of these approaches yields a 3D problem with a defective boundary condition, which could be tackled by one of the strategies described in Section 4.4. Formaggia et al. (Reference Formaggia, Moura and Nobile2007) and Papadakis (Reference Papadakis2009) have successfully considered explicit algorithms based on the solution of the 3D and 1D problems only once per time step. These algorithms enforce a limitation on
![]() $\unicode[STIX]{x1D6E5}t$
, which, however, is milder with respect to that imposed by the numerical scheme adopted for the 1D model. As an alternative, Blanco, Feijóo and Urquiza (Reference Blanco, Feijóo and Urquiza2007) and Blanco et al. (Reference Blanco, Pivello, Urquiza and Feijóo2009) have introduced iterative methods applied directly to the monolithic linearized system. A different approach to solving the 3D/1D coupled problem relies on writing an interface equation involving only the 3D/1D interface unknowns. We can interpret this equation as the geometric heterogeneous counterpart of the Schur complement equation. For its numerical solution, Leiva, Blanco and Buscaglia (Reference Leiva, Blanco and Buscaglia2011), Malossi et al. (Reference Malossi, Blanco, Crosetto, Deparis and Quarteroni2013) and Blanco, Deparis and Malossi (Reference Blanco, Deparis and Malossi2013) have used either the Broyden or the Newton method, in combination with GMRES. Methods relying on the numerical solution of the interface equation are simple to implement in the case of multiple interfaces, such as those arising in complex arterial networks.
$\unicode[STIX]{x1D6E5}t$
, which, however, is milder with respect to that imposed by the numerical scheme adopted for the 1D model. As an alternative, Blanco, Feijóo and Urquiza (Reference Blanco, Feijóo and Urquiza2007) and Blanco et al. (Reference Blanco, Pivello, Urquiza and Feijóo2009) have introduced iterative methods applied directly to the monolithic linearized system. A different approach to solving the 3D/1D coupled problem relies on writing an interface equation involving only the 3D/1D interface unknowns. We can interpret this equation as the geometric heterogeneous counterpart of the Schur complement equation. For its numerical solution, Leiva, Blanco and Buscaglia (Reference Leiva, Blanco and Buscaglia2011), Malossi et al. (Reference Malossi, Blanco, Crosetto, Deparis and Quarteroni2013) and Blanco, Deparis and Malossi (Reference Blanco, Deparis and Malossi2013) have used either the Broyden or the Newton method, in combination with GMRES. Methods relying on the numerical solution of the interface equation are simple to implement in the case of multiple interfaces, such as those arising in complex arterial networks.
In Figure 4.8 we give a numerical result obtained by the coupling between the 3D model of an ascending aorta and a 1D model of the systemic circulation. This result highlights the suitability of the 1D model in providing absorbing conditions for the 3D model and in propagating the pressure wave along the whole network (Malossi Reference Malossi2012).
PART TWO
Heart function
5 Basic facts on quantitative physiology
5.1 Basic anatomy
The heart is a hollow organ that pumps the blood into the arteries of the systemic and pulmonary circulations and collects it after its return through the veins. It is made up of the left and right heart, each consisting of two chambers, an atrium and a ventricle. The left and right hearts are separated by the interatrial and interventricular septa, which do not allow the transfer of blood, whereas the atria and the ventricles are connected by the atrioventricular valves (tricuspid valve in the right heart, mitral valve in the left heart) that either allow or prevent the blood transfer from the atria to the ventricles depending on their position (open or closed, respectively): see Figure 5.1. In particular, they open when the atrial pressure is higher than the ventricular pressure and close as soon as the blood flow rate becomes negative, that is, when blood flow, which normally goes from the atrium to the ventricle, comes back into the atrium. The papillary muscles, located in the ventricles, attach to the cusps of these valves via the chordae tendineae, preventing their inversion (prolapse) during closure.

Figure 5.1. Schematic representation of the heart.
All four chambers are connected to the circulatory system: the left ventricle through the aorta, the right ventricle through the pulmonary artery, the left atrium through the pulmonary veins, and the right atrium through the superior and inferior venae cavae. The ventricles are separated from the circulatory system by two further valves, the aortic valve on the left side and the pulmonary valve on the right side, whose opening/closure mechanism is similar to that of the atrioventricular valves, that is, they open when the pressure is higher in the ventricle with respect to the corresponding connected artery, whereas they close when the flow rate becomes negative (i.e. going from the artery to the ventricle). No valves are located between the atria and the corresponding terminal veins.
The heart wall is made up of three layers: the internal thin endocardium, the thick muscular myocardium and the external thin epicardium. The myocardium of the left ventricle is almost twice as thick as that of the right ventricle. The epicardium is surrounded by the pericardium, a serous membrane that isolates the heart from the closest organs, facilitating its movements.
5.2 The cardiac cycle
The main purpose of the heart is to pump the blood in the circulatory system through the aorta and the pulmonary artery. To do this, it needs to exceed the resistance in the arteries where blood has a non-null pressure (about
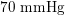 $70~\text{mmHg}$
in the aorta,
$70~\text{mmHg}$
in the aorta,
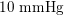 $10~\text{mmHg}$
in the pulmonary artery) due to the reaction of the elastic vessel wall to the deformation induced by blood inside. Moreover, the heart supplies blood with the energy needed to reach the microvasculature or the lungs. The total work done by the heart per heartbeat is
$10~\text{mmHg}$
in the pulmonary artery) due to the reaction of the elastic vessel wall to the deformation induced by blood inside. Moreover, the heart supplies blood with the energy needed to reach the microvasculature or the lungs. The total work done by the heart per heartbeat is
 $$\begin{eqnarray}W=QP+\frac{1}{2}mv^{2},\end{eqnarray}$$
$$\begin{eqnarray}W=QP+\frac{1}{2}mv^{2},\end{eqnarray}$$
where
![]() $Q$
and
$Q$
and
![]() $m$
are the blood flow rate and mass ejected,
$m$
are the blood flow rate and mass ejected,
![]() $P$
is the arterial blood pressure, and
$P$
is the arterial blood pressure, and
![]() $v$
is the blood velocity in the aorta or pulmonary artery. The kinetic component of the work is quite negligible with respect to the potential component (about
$v$
is the blood velocity in the aorta or pulmonary artery. The kinetic component of the work is quite negligible with respect to the potential component (about
![]() $2\%$
for the left heart and about
$2\%$
for the left heart and about
![]() $5\%$
for the right heart), although it could become more relevant (up to
$5\%$
for the right heart), although it could become more relevant (up to
![]() $25\%$
) under physical effort. The flow rate
$25\%$
) under physical effort. The flow rate
![]() $Q$
in normal conditions is about
$Q$
in normal conditions is about
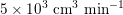 $5\times 10^{3}~\text{cm}^{3}~\text{min}^{-1}$
, so that, assuming
$5\times 10^{3}~\text{cm}^{3}~\text{min}^{-1}$
, so that, assuming
![]() $60$
–
$60$
–
![]() $90$
heartbeats per minute, we have about
$90$
heartbeats per minute, we have about
![]() $55.5$
–
$55.5$
–
 $83.3~\text{cm}^{3}$
of blood expelled at each heartbeat. The energetic requirements for pumping blood are obtained, as in all organs, by the consumption of oxygen that is provided to the heart by blood in the coronary arteries. The efficiency of the heart, that is, the ratio between the energy
$83.3~\text{cm}^{3}$
of blood expelled at each heartbeat. The energetic requirements for pumping blood are obtained, as in all organs, by the consumption of oxygen that is provided to the heart by blood in the coronary arteries. The efficiency of the heart, that is, the ratio between the energy
![]() $W$
and the total energy consumption, is in physiological cases about
$W$
and the total energy consumption, is in physiological cases about
![]() $25\%$
.
$25\%$
.
The cardiac cycle comprises different phases. For its description, we consider the left heart and we start from the situation where the left atrium is filled with oxygenated blood coming from the pulmonary veins, the mitral valve is closed, and the left ventricle has reached its maximum contraction.
-
(1) Ventricular filling. Due to the continuous inflation of blood, when the pressure in the atrium exceeds the ventricular pressure (about
 $10~\text{mmHg}$
) the mitral valve opens. Blood starts filling the left ventricle, which relaxes. In an initial stage (
$10~\text{mmHg}$
) the mitral valve opens. Blood starts filling the left ventricle, which relaxes. In an initial stage (
 ${\sim}\,$
0.15 s), there is fast inflation of blood due to the pressure gradient between the atrium and the ventricle, where the ventricle probably also exerts suction due to its expansion (phase 1a in Figure 5.2). In any case, this is a passive phase. In a second stage (
${\sim}\,$
0.15 s), there is fast inflation of blood due to the pressure gradient between the atrium and the ventricle, where the ventricle probably also exerts suction due to its expansion (phase 1a in Figure 5.2). In any case, this is a passive phase. In a second stage (
 ${\sim}\,$
0.25 s, phase 1b in Figure 5.2), the atrium actively contracts (atrial systole), producing a slow ventricular inflation of the remaining blood.
${\sim}\,$
0.25 s, phase 1b in Figure 5.2), the atrium actively contracts (atrial systole), producing a slow ventricular inflation of the remaining blood. -
(2) Isovolumic contraction. After the atrial systole, the ventricular active contraction starts. This produces an increase in the ventricular pressure causing retrograde flow that accordingly closes the mitral valve. However, the ventricular pressure is still lower than the aortic pressure, so the aortic valve is also closed. Thus, during this phase, there is a continuous and fast increase of ventricular pressure without any change of blood volume due to blood incompressibility (
 ${\sim}\,$
0.05 s, phase 2 in Figure 5.2).
${\sim}\,$
0.05 s, phase 2 in Figure 5.2). -
(3) Ventricular ejection. As soon as the ventricular pressure reaches the aortic pressure (about
 $70~\text{mmHg}$
), the aortic valve opens and blood is ejected into the systemic circulation. Since the ventricular contraction carries on after the valve opens, the ventricular pressure continues to increase. Accordingly, the aortic pressure also increases due to the elastic adaptation of the vessel wall. However, at each time, there is a pressure difference between ventricle and aorta that allows blood to accelerate (
$70~\text{mmHg}$
), the aortic valve opens and blood is ejected into the systemic circulation. Since the ventricular contraction carries on after the valve opens, the ventricular pressure continues to increase. Accordingly, the aortic pressure also increases due to the elastic adaptation of the vessel wall. However, at each time, there is a pressure difference between ventricle and aorta that allows blood to accelerate (
 ${\sim}\,$
0.05 s, phase 3a in Figure 5.2). When the ventricle stops its active contraction, this pressure difference reduces and, after a short period (but not immediately due to inertial effects), becomes zero, allowing the flow rate to reach its maximum (
${\sim}\,$
0.05 s, phase 3a in Figure 5.2). When the ventricle stops its active contraction, this pressure difference reduces and, after a short period (but not immediately due to inertial effects), becomes zero, allowing the flow rate to reach its maximum (
 ${\sim}\,$
0.05 s, phase 3b in Figure 5.2). Then, the pressure difference starts to become negative (higher in the aorta), provoking a deceleration of blood that however continues to enter the aorta. When, due to this deceleration, the flow rate becomes negative, the aortic valve closes and the blood ejection stops (
${\sim}\,$
0.05 s, phase 3b in Figure 5.2). Then, the pressure difference starts to become negative (higher in the aorta), provoking a deceleration of blood that however continues to enter the aorta. When, due to this deceleration, the flow rate becomes negative, the aortic valve closes and the blood ejection stops (
 ${\sim}\,$
0.15 s, phase 3c in Figure 5.2). Note that, once the active contraction stops, the ventricle starts to relax, releasing the elastic energy accumulated during the contraction. However, this energetic relaxation is not immediately followed by a mechanical relaxation, which should result in an increase in ventricular volume. Indeed, due to inertial effects, there is a ‘passive’ mechanical contraction which allows ejection of all the blood.
${\sim}\,$
0.15 s, phase 3c in Figure 5.2). Note that, once the active contraction stops, the ventricle starts to relax, releasing the elastic energy accumulated during the contraction. However, this energetic relaxation is not immediately followed by a mechanical relaxation, which should result in an increase in ventricular volume. Indeed, due to inertial effects, there is a ‘passive’ mechanical contraction which allows ejection of all the blood. -
(4) Isovolumic relaxation. When the aortic valve closes, the release of energy of the ventricle continues with both valves closed, so that no changes in ventricular volume are produced, resulting in fast decrease of the ventricular pressure (
 ${\sim}\,$
0.10 s, phase 4 in Figure 5.2). After the valve closure, the aortic pressure continues to increase (slightly), due to the elastic recoil of the closing valve (dicrotic wave: see Figure 5.2).
${\sim}\,$
0.10 s, phase 4 in Figure 5.2). After the valve closure, the aortic pressure continues to increase (slightly), due to the elastic recoil of the closing valve (dicrotic wave: see Figure 5.2).
All these mechanisms apply to the right heart too, the only difference being the pressure values, smaller in this case. This justifies the thicker myocardium of the left heart since higher values of resistances need to be exceeded.

Figure 5.2. Aortic pressure, ventricular pressure, atrial pressure and ventricular volume during a heartbeat.
5.3 Electrical propagation
As seen in the previous paragraph, the main agent of blood ejection in the circulatory system is active ventricular contraction. The heart itself is able to produce the electrical impulse that determines this contraction, triggered by an electrical potential that propagates along all the myocardium. This is possible owing to the excitability of the heart cells, the cardiomyocytes, which, when suitably stimulated, are able to produce a variation in membrane voltage. At rest, the membrane potential is negative (
![]() ${\sim}-90$
mV), whereas when stimulated it reaches a positive value (
${\sim}-90$
mV), whereas when stimulated it reaches a positive value (
![]() ${\sim}\,$
20 mV) in a very short period (about 2 ms). After this depolarization, a plateau around 0 mV is observed that corresponds to the refractory period (see Figure 5.3). Then, the repolarization phase starts, which brings the potential back to the rest value allowing for a new excitation (see Figure 5.3(a)). This action potential is generated by several ion channels that open and close, and by the resulting currents passing through the membrane. The most important channels are those of calcium, sodium and potassium. In particular, a fast inward sodium current is the main driver of rapid depolarization, a slow inward flux of extra-cellular calcium ions is the main agent behind the characteristic plateau appearing after the depolarization, whereas the outward potassium currents are responsible for the repolarization.
${\sim}\,$
20 mV) in a very short period (about 2 ms). After this depolarization, a plateau around 0 mV is observed that corresponds to the refractory period (see Figure 5.3). Then, the repolarization phase starts, which brings the potential back to the rest value allowing for a new excitation (see Figure 5.3(a)). This action potential is generated by several ion channels that open and close, and by the resulting currents passing through the membrane. The most important channels are those of calcium, sodium and potassium. In particular, a fast inward sodium current is the main driver of rapid depolarization, a slow inward flux of extra-cellular calcium ions is the main agent behind the characteristic plateau appearing after the depolarization, whereas the outward potassium currents are responsible for the repolarization.

Figure 5.3. (a) Characteristic action potential of cardiomyocytes and (b) anatomy of the cardiac conduction system (http://medical-dictionary.thefreedictionary.com).
Unlike other cells in the human body, the cardiomyocytes obey the ‘all-or-none’ law, meaning that if the stimulus is above a suitable threshold, a complete action potential with peak value independent of the stimulus is generated, otherwise no response is provided by the cell. Another characteristic of the heart cells is the presence of a refractory period after the generation of an action potential, which inhibits any further stimulus independently of its intensity. Thus, during this period the cell is not excitable at all (absolute refractory period, infinite threshold). Afterwards, the cardiomyocytes recover their excitability with a value of the threshold needed to generate the action potential which decreases in time (relative refractory period). Finally, once the threshold value reaches its minimum, the cell returns to its excitable state and the threshold remains constant.
The cardiomyocytes act as a syncytium, that is, the stimulation of an individual cell produces the action potential and the corresponding current that results in the excitation of the neighbour cells, and thus of the whole myocardium. This is due to the gap junctions, intercellular channels characterized by low resistance and located between cardiomyocytes that permit the electrical potential to travel on the cellular membranes from cell to cell.
In normal conditions, the signal spontaneously originates at the sinoatrial node, located in the right atrium at the junction with the superior vena cava. It is the natural pacemaker of the heart, and imposes its rhythm on the entire myocardium (sinusal rhythm,
![]() ${\sim}\,$
60–90 heartbeats per minute). The impulse generated by the sinoatrial node propagates through all the cardiomyocytes of the atria, activating all their regions and allowing their contraction. The propagation is faster in the direction of the ventricles (
${\sim}\,$
60–90 heartbeats per minute). The impulse generated by the sinoatrial node propagates through all the cardiomyocytes of the atria, activating all their regions and allowing their contraction. The propagation is faster in the direction of the ventricles (
![]() ${\sim}\,$
200
${\sim}\,$
200
![]() $~\text{cm}~\text{s}^{-1}$
), allowing it to reach the atrioventricular node, located between the atria and the ventricles. When the signal arrives at this node, it is subjected to a delay (
$~\text{cm}~\text{s}^{-1}$
), allowing it to reach the atrioventricular node, located between the atria and the ventricles. When the signal arrives at this node, it is subjected to a delay (
![]() ${\sim}\,$
0.12 s) that allows complete contraction of the atria before the propagation in the ventricles starts. Moreover, this node provides a filter limiting possible high frequencies of the atrial signal, induced by atrial fibrillation, for example, protecting the ventricles. This node, when the sinoatrial node loses automatic function, becomes the leading pacemaker and takes on the role of giving the pace to all ventricle stimulation. Then, the electrical signal enters the bundle of His, propagating in the ventricles through the two (left and right) bundle branches and then through the Purkinje fibres (see Figure 5.3(b)). The bundle of His, bundle branches and Purkinje fibres form the cardiac conduction system (CCS), a subendocardial specialized network responsible for the fast and coordinated propagation of electrical impulses in the ventricle. The propagation in the CCS is very fast (
${\sim}\,$
0.12 s) that allows complete contraction of the atria before the propagation in the ventricles starts. Moreover, this node provides a filter limiting possible high frequencies of the atrial signal, induced by atrial fibrillation, for example, protecting the ventricles. This node, when the sinoatrial node loses automatic function, becomes the leading pacemaker and takes on the role of giving the pace to all ventricle stimulation. Then, the electrical signal enters the bundle of His, propagating in the ventricles through the two (left and right) bundle branches and then through the Purkinje fibres (see Figure 5.3(b)). The bundle of His, bundle branches and Purkinje fibres form the cardiac conduction system (CCS), a subendocardial specialized network responsible for the fast and coordinated propagation of electrical impulses in the ventricle. The propagation in the CCS is very fast (
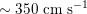 ${\sim}350~\text{cm}~\text{s}^{-1}$
), and its role is to reach the entire endocardium via the dense network of Purkinje fibres, activating it almost simultaneously. Note that the cells of the CCS are dedicated to electrical propagation, so they are not involved in the muscular contraction. Then, the electrical signal enters the myocardium through the Purkinje muscle junctions which are the terminal points of the Purkinje network. At the Purkinje muscle junctions, the signal is subjected to a delay (
${\sim}350~\text{cm}~\text{s}^{-1}$
), and its role is to reach the entire endocardium via the dense network of Purkinje fibres, activating it almost simultaneously. Note that the cells of the CCS are dedicated to electrical propagation, so they are not involved in the muscular contraction. Then, the electrical signal enters the myocardium through the Purkinje muscle junctions which are the terminal points of the Purkinje network. At the Purkinje muscle junctions, the signal is subjected to a delay (
![]() ${\sim}\,$
0.01 s) and then propagates into the ventricular muscle towards the epicardium with reduced velocity (
${\sim}\,$
0.01 s) and then propagates into the ventricular muscle towards the epicardium with reduced velocity (
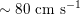 ${\sim}80~\text{cm}~\text{s}^{-1}$
).
${\sim}80~\text{cm}~\text{s}^{-1}$
).
To better understand how the propagation of the electrical potential spreads into the ventricles, we observe that cardiomyocytes are of cylindrical type. This allows us to define the fibre direction of the cell, resulting in a macroscopic fibre direction intended as the average cell orientation in a sufficiently small control volume. A transmural variation of the fibre direction is measured between the epicardium and the endocardium (
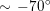 ${\sim}\,-70^{\circ }$
and
${\sim}\,-70^{\circ }$
and
![]() ${\sim}\,80^{\circ }$
with respect to the normal direction to the surface, respectively). The fibres are in turn organized into sheets of collagen. The velocity of propagation of the electrical potential is about twice as fast along the fibre direction compared to the directions tangential to the fibres.
${\sim}\,80^{\circ }$
with respect to the normal direction to the surface, respectively). The fibres are in turn organized into sheets of collagen. The velocity of propagation of the electrical potential is about twice as fast along the fibre direction compared to the directions tangential to the fibres.
5.4 Mechanisms of contraction and cardiac blood fluid dynamics
The propagation of the electrical signal through the cardiomyocytes is responsible for their contraction (electromechanical coupling), resulting in the atrial and, more importantly, ventricular contractions. The characteristic connections between the cardiomyocytes resulting in a syncytium allows coordinated contraction of the heart.
At the cellular level, as discussed in the previous paragraph, there is an inward flux of extra-cellular calcium ions just after the depolarization of the cell. Once in the intracellular space, calcium ions bind to troponin, which allows myosin to bind to actin and contraction of the cell to occur.
At the macroscopic level, ventricle contraction results in a longitudinal shortening (from apex to base) of about
![]() $15\%$
from the diastolic configuration, in a ventricular wall thickening of about
$15\%$
from the diastolic configuration, in a ventricular wall thickening of about
![]() $30\%$
, and torsion around the longitudinal axis of about
$30\%$
, and torsion around the longitudinal axis of about
![]() $15^{\circ }$
. This is due to the particular fibre orientation of the cardiomyocytes, which also highly influences the mechanical response of the heart.
$15^{\circ }$
. This is due to the particular fibre orientation of the cardiomyocytes, which also highly influences the mechanical response of the heart.
The heart obeys the Frank–Starling law, stating that an increase (for any reason) of the end diastolic volume (i.e. the maximum ventricular expansion) results in an increase in the stroke volume, that is, the volume of blood pumped by the left ventricle per heartbeat. This is due to an increase in the load experienced by the cardiomyocytes as a result of the increased volume of blood filling the ventricle. This extra stretching of the cells produces a greater number of actin–myosin bridges, resulting in augmented muscle contraction power. It should be noticed, however, that the Frank–Starling law holds true only up to a certain level of increased stretch: for higher values, the contractility power of the heart, and thus the stroke volume, decreases.
As well as the influence of electrical processes on mechanical behaviour, cardiomyocytes also experience mechano-electrical feedback. This is due to the formation of stretch-activated ion channels and to changes in cell conductivity by means of stretching the cell, which changes the membrane shape and the distance between gap junctions. This mechanism seems to be of utmost importance in describing the evolution of spiral waves and thus arrhythmias (Trayanova et al. Reference Trayanova, Li, Eason and Kohl2004, Keldermann, Nash and Panfilov Reference Keldermann, Nash and Panfilov2009).
Blood flow in the cardiac chambers exhibits different characteristics with respect to the vascular flow. The particular challenges are the large-scale motion and complex deformation of the myocardium, the complex interaction with valves leading to specific flow patterns, and the higher Reynolds number (about
![]() $4000$
). For some authors, all of these aspects are responsible for transition to turbulence effects, especially in pathological conditions, even though not all authors agree that turbulence can also occur in normal conditions. Another important aspect of cardiac blood flow is given by the formation of a large vortex ring in the long axis plane of the left ventricle due to the asymmetry of the mitral valve leaflets that forces the blood flow jet to impinge on the posterior wall (Charonko et al.
Reference Charonko, Kumar, Stewart, Little and Vlachos2013). The interaction of this ring with the wall gives rise to a complex flow pattern. Complex vortex rings ejected by the pulmonary veins can also be observed in the left atrium (Mittal et al.
Reference Mittal, Seo, Vedula, Choi, Liu, Huang, Jain, Younes, Abraham and George2016).
$4000$
). For some authors, all of these aspects are responsible for transition to turbulence effects, especially in pathological conditions, even though not all authors agree that turbulence can also occur in normal conditions. Another important aspect of cardiac blood flow is given by the formation of a large vortex ring in the long axis plane of the left ventricle due to the asymmetry of the mitral valve leaflets that forces the blood flow jet to impinge on the posterior wall (Charonko et al.
Reference Charonko, Kumar, Stewart, Little and Vlachos2013). The interaction of this ring with the wall gives rise to a complex flow pattern. Complex vortex rings ejected by the pulmonary veins can also be observed in the left atrium (Mittal et al.
Reference Mittal, Seo, Vedula, Choi, Liu, Huang, Jain, Younes, Abraham and George2016).
5.5 A brief summary of heart diseases
The principal heart diseases (cardiopathies) are ischaemic cardiopathy, the cardiomyopathies, hypertensive cardiopathy and valvular pathologies.
Ischaemic cardiopathy is the most important in terms of frequency and clinical impact. It is caused by a reduced coronary flow rate (due to atherosclerosis of coronary arteries) with consequent malnutrition of the myocardium. When, due to coronary occlusion, a decrease in oxygen supply is abrupt, long-lasting and total, an infarct of the myocardium occurs. This is the most classical event of ischaemic cardiopathy, resulting in necrosis of cardiomyocytes and leading, at the end of the process, to the formation of a scar.
In dilated cardiomyopathy the ventricle wall becomes thinner due to the partial replacement of cardiomyocytes with fibrosis and small scars, leading to dilatation of the ventricle. In hypertrophic cardiomyopathy the ventricular wall thickens, with a consequent increase in ventricular blood pressure resulting in decreased filling of the ventricle. As in all cases of ventricular hypertrophy, this produces malnutrition of the myocardium, since the amount of blood supplied by the coronary arteries remains unchanged. Moreover, in this specific hypertrophic cardiomyopathy, the orientation of the fibres is not coordinated as in normal conditions (this is called electrical disarray).
In hypertensive cardiopathy there is an increase in blood pressure, resulting in increased work needed by the heart to pump blood, leading again to thickening of the myocardial wall and to malnutrition of the myocardium.
The main valvular pathologies are stenosis and insufficiency. In aortic valve stenosis, narrowing of the maximum opening of the aortic valve causes the heart to require increased work to pump blood into the aorta properly, again resulting in thickening of the myocardial wall and malnutrition. In mitral valve stenosis, there is an increase in the pressure of the left atrium and in the pulmonary circulation, with consequences for the right heart. Aortic and mitral valve insufficiency is due to the partial reversal of flow (going from the aorta to the left ventricle in aortic insufficiency, and from the left ventricle to the left atrium in mitral insufficiency), which occurs as a consequence of inadequate closure of the valve. In this case the heart dilates in order to supply this retrograde flow, resulting in an increase in its contraction power due to the Frank–Starling law. However, sooner or later the diastolic cell stretching overcomes the threshold of validity of the Frank–Starling law, resulting in decreased contractility power.
The two main events, possibly fatal, that the heart may encounter as a consequence of these cardiopathies are cardiac arrest, due to ventricular fibrillation, and heart failure.
In ventricular fibrillation, the cardiomyocytes are not excited in a coordinated way and thus do not contract homogeneously; instead, groups of cells contract continuously whereas other groups relax. This chaotic excitation, if the fibrillation continues, inhibits the normal functioning of the heart pump, which is no longer able to pump the blood around the circulatory system regularly, leading finally to death. All the cardiopathies described above could yield altered electrical properties (i.e. velocity of conduction and refractoriness), which could lead to ventricular fibrillation. For example, in a myocardial infarct, the arrhythmogenic substrate is formed by a matrix of healthy cardiomyocytes, necrotic cardiomyocytes and scars, whereas in hypertrophic cardiomyopathy it is provided by the electrical disarray.
When the blood pumped by the heart at each heartbeat is less than the amount required by the body (but not absent as in ventricular fibrillation), the heart on the one hand increases its frequency so as to guarantee that the blood ejected per minute (cardiac output) is almost normal, and on the other hand it increases its diastolic filling to increase the stroke volume. However, the increase in frequency (tachycardia) is energetically disadvantageous for the heart, and possible excessive diastolic cell stretching leads to the loss of validity of the Frank–Starling law. When these two compensating mechanisms are no longer effective, cardiac output dramatically decreases, leading to heart failure. In the absence of other causes of death (cardiac arrest or death for non-cardiac reasons), all the cardiopathies described above will sooner or later lead to heart failure.
6 All about data
As discussed in Section 3, the use of patient-specific data is needed for numerical modelling aiming to understand biophysical processes and support clinicians. This also holds true for heart modelling. The latter accounts for three processes that are intimately coupled: electrical propagation, mechanical contraction and relaxation, and the blood fluid dynamics. The first two processes occur in the cardiac tissue (here called the muscle region), whereas the latter occurs in the four hollow regions (chambers) delimited by the endocardium. As in Section 3 for the circulatory system, in what follows we briefly discuss how to obtain geometric, boundary and biological cardiac data.
6.1 Cardiac geometric data
Referring to Figure 6.1, we need to build two computational domains: the muscle region
![]() $\unicode[STIX]{x1D6FA}_{\mathit{mus}}$
, delimited by the external surface of the epicardium
$\unicode[STIX]{x1D6FA}_{\mathit{mus}}$
, delimited by the external surface of the epicardium
![]() $\unicode[STIX]{x1D6F4}_{\mathit{epi}}$
and by the internal surface of the endocardium
$\unicode[STIX]{x1D6F4}_{\mathit{epi}}$
and by the internal surface of the endocardium
![]() $\unicode[STIX]{x1D6F4}_{\mathit{endo}}$
, and the cavities
$\unicode[STIX]{x1D6F4}_{\mathit{endo}}$
, and the cavities
![]() $\unicode[STIX]{x1D6FA}_{\mathit{cav}}$
, referred to below as heart cavities or chambers, delimited by the endocardium. The cavities are easily obtained once the endocardium has been reconstructed, so that in fact the cardiac image reconstruction process relies on identifying the endocardium and epicardium surfaces.
$\unicode[STIX]{x1D6FA}_{\mathit{cav}}$
, referred to below as heart cavities or chambers, delimited by the endocardium. The cavities are easily obtained once the endocardium has been reconstructed, so that in fact the cardiac image reconstruction process relies on identifying the endocardium and epicardium surfaces.

Figure 6.1. Longitudinal section of a complete heart domain.
This problem presents several challenging issues. In the vascular case, the external wall surface is usually obtained by extruding the internal surface under the assumption of constant (or in any case known) wall thickness (see Section 3.1.3). This procedure is unsuitable for the reconstruction of the myocardium. On one hand, the thickness changes significantly while moving from apex to base. On the other hand, changes can be dramatic from patient to patient. Moreover, due to the large displacements induced by heart motion, a dynamic acquisition procedure (allowing for the acquisition of several frames per heartbeat) is required to obtain a reconstruction of the heart other than at the end-diastolic phase. Finally, the presence of the papillary muscle and wall irregularities given by trabeculations makes the reconstruction of the endocardium very problematic.
Let us briefly review the most common radiological procedures for acquisition of cardiac images. As in the vascular case, MRI and CT play a major role. Often, due to heart motion, temporally resolved acquisitions are performed, allowing us to obtain 20–30 frames per heartbeat.
The main interest is in the left ventricle, due to its vital importance and its pronounced thickness, ranging between
![]() $6$
and
$6$
and
![]() $16~\text{mm}$
. The shape of its cavity is often approximated by an ellipsoid. In contrast, the right ventricle and the atria are characterized by a thickness that usually does not reach the spatial resolution of the acquisition technologies, so their reconstruction is hard and consequently less studied.
$16~\text{mm}$
. The shape of its cavity is often approximated by an ellipsoid. In contrast, the right ventricle and the atria are characterized by a thickness that usually does not reach the spatial resolution of the acquisition technologies, so their reconstruction is hard and consequently less studied.
The standard cardiac acquisition plane is orthogonal to the long axis. Blood appears brighter whereas the myocardium and the surrounding tissue are darker: see Figure 6.2. Not all of the slices share the same degree of complexity in their reconstruction. In particular, apical and basal (upward) slice images are more difficult to segment than mid-ventricular slices.
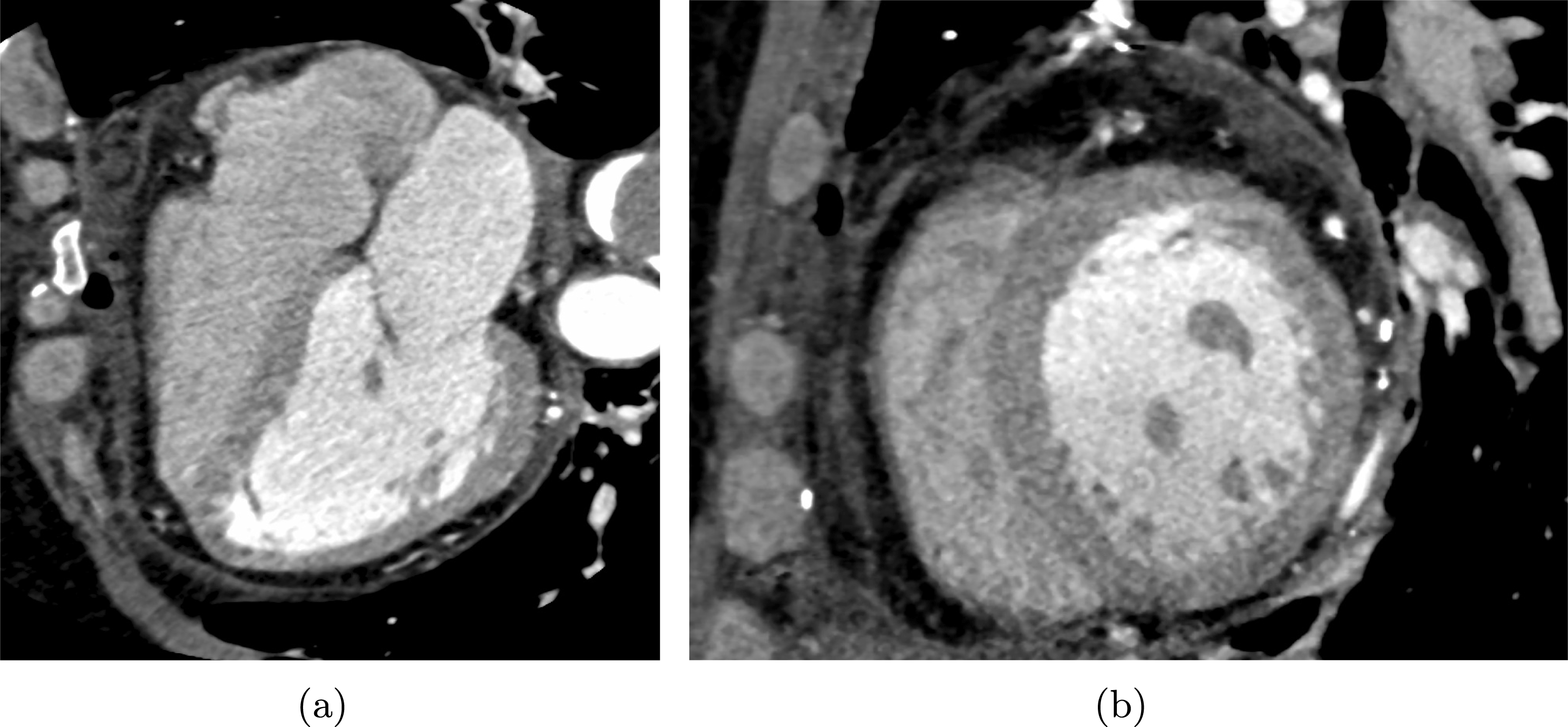
Figure 6.2. (a) Longitudinal CT slice of the heart. Right atrium (top left), right ventricle (bottom left), left atrium (top right), left ventricle (bottom right). (b) CT slice in the plane orthogonal to the long axis. In both figures, on the right the thick left ventricle myocardium is detectable in darker grey. Radiological images from Ospedale Sacco, Milan, Italy.
Before the ventricle segmentation starts, a preliminary localization procedure is performed, in order to identify a region of interest and reduce the computational effort. This step is usually performed automatically, taking advantage of the movement of the heart on a fixed background: see e.g. Cocosco et al. (Reference Cocosco, Netsch, Sénǵas, Bystrov, Niessen and Viergever2004). Another automatic heart location is based on extracting rectangular subwindows from the image and computing specific features for them. Then, based on a priori chosen class, the subwindows satisfying specific features are recognized as belonging to the heart.
An initial class of ventricle segmentation methods makes use of little (or even no) a priori information. Usually in these methods the endocardium is first segmented by means of thresholding (see Section 3 and Goshtasby and Turner Reference Goshtasby and Turner1995). Alternatively, dynamic programming methods have been considered, where the optimal path in a cost matrix is sought, assigning a low cost to boundaries. Taking advantage of the circular shape of the ventricle, polar coordinates are used and one-dimensional search is performed (Gupta et al. Reference Gupta, von Kurowski, Singh, Geiger, Liang, Chiu, Adler, Haacke and Wilson1993). In order to exclude papillary muscles from the segmentation, possible strategies are the computation of the convex hull of the contour (van der Geest, Jansen, Buller and Reiber Reference van der Geest, Jansen, Buller and Reiber1994) or a smoothing of the latter by fitting a parametric curve (Waiter et al. Reference Waiter, Mckiddie, Redpath, Semple and Trent1999). As in the vascular case, deformable models are used for cardiac segmentation (see Section 3). In particular, the functional to be minimized often includes a regularization term to control the smoothness of the reconstructed curves (Pham, Xu and Prince Reference Pham, Xu and Prince2000).
Specific automatic methods that have been developed for cardiac image segmentation are based on strong a priori information concerning the shape of the ventricles, which is included in the segmentation algorithm by means of statistical models. These strategies are suited to cardiac segmentation because variability in heart shape among patients, as opposed to arteries, is very small in normal conditions. These statistical model-based segmentation strategies rely on identifying an average shape of available geometries forming a training set, and modelling the variability within the latter. This is usually done by means of principal component analysis of positions and, if needed, displacements, allowing computation of the eigenvalues and eigenvectors of the covariance matrix related to the training set. These strategies allow automatic segmentation without user intervention, at the expense of needing a training set. For example, deformable models have been extended to this framework by adding a term to the functional to be minimized that penalizes the distance to a reference model (e.g. the mean shape of the training set). Another very common statistical model-based strategy is atlas-guided segmentation. Given an atlas, that is, an integrated image from multiple segmentations, a registration procedure is performed based on mapping the coordinates of the image under investigation to those of the atlas (Lorenzo-Valdés et al. Reference Lorenzo-Valdés, Sanchez-Ortiz, Elkington, Mohiaddin and Rueckert2004). This transformation is then applied to the atlas obtaining the final segmentation. The registration process could be based on non-rigid transformations that account for elastic deformations. For a recent review of cardiac segmentation methods we refer to Petitjean and Dacher (Reference Petitjean and Dacher2011).
Finally, we observe the importance of including the fibre orientation in the reconstructed geometries with respect to modelling electrical propagation and mechanical contraction in the muscle region. Indeed, as discussed in Section 5, the conduction velocity of the action potential propagation assumes different values along the fibres than in the tangential direction. Moreover, the stretching ability of the myocardium is facilitated along the fibre direction.
Diffusion-tensor-MRI is an MRI technology able to identify fibre orientation, but it is not yet used every day in clinical practice, and it is difficult to apply because of heart movement. See Nagler et al. (Reference Nagler, Bertoglio, Stoeck, Kozerke, Wall and van Assen2015) for a preliminary study of the cardiac fibre estimation using synthetic diffusion-tensor-MRI datasets. Analytical representations of the fibres, suitably mapped onto the geometry under investigation, have been proposed to supply the lack of information provided by the imaging. For example, Peskin (Reference Peskin1989) described fibres as geodesics, whereas Pravdin et al. (Reference Pravdin, Berdyshev, Panfilov, Katsnelson, Solovyova and Markhasin1989) represented them by means of spiral surfaces. Other strategies are based on computational generation of the fibre orientation to provide a plausible configuration, for example by means of the solution of a Poisson equation (Bayer et al. Reference Bayer, Blake, Plank and Trayanova2012, Rossi et al. Reference Rossi, Lassila, Ruiz-Baier, Sequeira and Quarteroni2014, Wong and Kuhl Reference Wong and Kuhl2014), or by using the unscented Kalman filter (Nagler et al. Reference Nagler, Bertoglio, Gee, Wall, Ourselin, Rueckert and Smith2013).
The Purkinje fibres are not detectable via classical radiological acquisition since their thickness falls below the spatial resolution. For this reason, Abboud, Berenfeld and Sadeh (Reference Abboud, Berenfeld and Sadeh1991), Sebastian et al. (Reference Sebastian, Zimmerman, Romero and Frangi2011) and Ijiri et al. (Reference Ijiri, Ashihara, Yamaguchi, Takayama, Igarashi, Shimada, Namba, Haraguchi and Nakazawa2008) proposed exploiting the fractal nature of these fibres to generate a realistic Purkinje network, whereas Vergara et al. (Reference Vergara, Palamara, Catanzariti, Nobile, Faggiano, Pangrazzi, Centonze, Maines, Quarteroni and Vergara2014), Palamara et al. (Reference Palamara, Vergara, Catanzariti, Faggiano, Centonze, Pangrazzi, Maines and Quarteroni2014) and Palamara et al. (Reference Palamara, Vergara, Faggiano and Nobile2015) have personalized such fractal networks to the patient at hand by including patient-specific measurements of the activation times (see Section 6.2 for a description of the latter).
For the muscle region mesh generation, the strategies described in Section 3 could be applied to cardiac geometries as well. For ideal ellipsoid geometries, usually considered in numerical experiments to test the performance of the numerical algorithms, structured hexahedral meshes are often used, exploiting the symmetry of the ventricles around the long axis: see e.g. Pavarino, Scacchi and Zampini (Reference Pavarino, Scacchi and Zampini2015). However, unstructured meshes composed of tetrahedra have also been considered (Goktepe and Kuhl Reference Goktepe and Kuhl2010), in particular for real geometries reconstructed by MRI or CT (see e.g. Rossi et al. Reference Rossi, Lassila, Ruiz-Baier, Sequeira and Quarteroni2014, Wong, Goktepe and Kuhl Reference Wong, Goktepe and Kuhl2013, Vergara et al. Reference Vergara, Lange, Palamara, Lassila, Frangi and Quarteroni2016), or for the atria (Virag et al.
Reference Virag, Jacquemet, Henriquez, Zozor, Blanc, Vesin, Pruvot and Kappenberger2002). Hybrid unstructured meshes composed of tetrahedra and hexahedra have also been successfully considered (Gurev et al.
Reference Gurev, Pathmanathan, Fattebert, Wen, Magerlein, Gray, Richards and Rice2015). We notice that for the solution of the mechanical problem in the muscle region, no particular requirements are needed for mesh generation, whereas for the electrical propagation problem, due to the very steep front (about 200
![]() $\unicode[STIX]{x03BC}$
m), the required mesh resolution should be at least of the order of 100
$\unicode[STIX]{x03BC}$
m), the required mesh resolution should be at least of the order of 100
![]() $\unicode[STIX]{x03BC}$
m in order to spatially resolve this front (Clayton and Panfilov Reference Clayton and Panfilov2008). For mesh generation of the heart chambers, in view of the numerical solution of the fluid dynamics problem, unstructured tetrahedral elements are often considered: see e.g. Mittal et al. (Reference Mittal, Seo, Vedula, Choi, Liu, Huang, Jain, Younes, Abraham and George2016). In this case the mesh resolution needs to be very fine, even smaller than that for CT or MRI technologies (
$\unicode[STIX]{x03BC}$
m in order to spatially resolve this front (Clayton and Panfilov Reference Clayton and Panfilov2008). For mesh generation of the heart chambers, in view of the numerical solution of the fluid dynamics problem, unstructured tetrahedral elements are often considered: see e.g. Mittal et al. (Reference Mittal, Seo, Vedula, Choi, Liu, Huang, Jain, Younes, Abraham and George2016). In this case the mesh resolution needs to be very fine, even smaller than that for CT or MRI technologies (
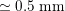 $\simeq 0.5~\text{mm}$
), in order to capture the complex flow structures that arise, particularly in the left atrium and left ventricle.
$\simeq 0.5~\text{mm}$
), in order to capture the complex flow structures that arise, particularly in the left atrium and left ventricle.
6.2 Cardiac boundary data
The acquisition of boundary data on electrical activation in the muscle region is now possible thanks to specific therapeutic techniques. For example, the NavX system is able to locate accurately any electrode catheter inserted in the heart chambers, providing accurate, real-time recording of the local endocardial electrical activity at a point in contact with the catheter (Eitel et al. Reference Eitel, Hindricks, Dagres, Sommer and Piorkowski2010, Vergara et al. Reference Vergara, Palamara, Catanzariti, Nobile, Faggiano, Pangrazzi, Centonze, Maines, Quarteroni and Vergara2014). In particular, this allows us to acquire endocardial maps of the activation times, defined as the time at which the action potential in a point reaches an intermediate value between the rest and the plateau potentials. However, this acquisition is performed only for specific therapeutic purposes, such as the ablation of anomalous electrical pathways.
For the mechanical problem involving the muscle region, data that are commonly available include the stresses exerted by the blood on the endocardium of the left ventricle and the endocardial and/or epicardial vessel wall displacements. Stresses are usually obtained from measurements of aortic pressure (see Section 3.2). This is a good approximation; as a matter of fact the ventricular and circulatory pressures are not the same (thus allowing the acceleration and deceleration of blood) but they are very similar: see Figure 5.2. Vessel wall displacements can be obtained from dynamic MRI or CT images, yielding 20–30 frames per heartbeat, providing the position of the endocardium and epicardium at multiple times. After suitable postprocessing, these techniques can provide an estimate of the vessel wall displacement (and thus velocity) by comparing two consecutive frames. The endocardial vessel wall velocity, thanks to a continuity argument, could also be interpreted as the blood velocity at the interface with the endocardium (Khalafvand, Zhong and Ng Reference Khalafvand, Zhong and Ng2014, Mittal et al. Reference Mittal, Seo, Vedula, Choi, Liu, Huang, Jain, Younes, Abraham and George2016).
Another useful measurement that could be provided quite easily by means of Doppler echocardiographic methods or PC-MRA (see Section 3.2) is the flow rate at the mitral and aortic valve orifices. With PC-MRA technology, measurement of blood velocity is possible in principle at any point of the ventricles and atria chambers.
In Section 7 we will see how these data can be used to provide boundary conditions for the different cardiac models we are about to introduce.
6.3 Cardiac biological data
The classical monodomain and bidomain models, widely used to describe the electrical propagation in the muscle region and Purkinje network (see Section 7.1), would require the following data: the membrane capacitance per unit area
![]() $C$
, the membrane surface-to-volume ratio
$C$
, the membrane surface-to-volume ratio
![]() $\unicode[STIX]{x1D712}$
, and the conductivities
$\unicode[STIX]{x1D712}$
, and the conductivities
![]() $\unicode[STIX]{x1D70E}$
(see the next section). Their subject-specific acquisition is generally out of reach. An acceptable range of values for the capacitance
$\unicode[STIX]{x1D70E}$
(see the next section). Their subject-specific acquisition is generally out of reach. An acceptable range of values for the capacitance
![]() $C_{m}$
in the myocardium is 0.8–1.0
$C_{m}$
in the myocardium is 0.8–1.0
![]() $\unicode[STIX]{x03BC}\text{F}~\text{cm}^{-2}$
(Roth Reference Roth1991, Huiskamp Reference Huiskamp1998); the capacitance
$\unicode[STIX]{x03BC}\text{F}~\text{cm}^{-2}$
(Roth Reference Roth1991, Huiskamp Reference Huiskamp1998); the capacitance
![]() $C_{p}$
in the Purkinje network is higher (
$C_{p}$
in the Purkinje network is higher (
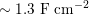 ${\sim}1.3~\unicode[STIX]{x03BC}\text{F}~\text{cm}^{-2}$
: Legato Reference Legato1973). The value of the membrane surface-to-volume ratio in the muscle region
${\sim}1.3~\unicode[STIX]{x03BC}\text{F}~\text{cm}^{-2}$
: Legato Reference Legato1973). The value of the membrane surface-to-volume ratio in the muscle region
![]() $\unicode[STIX]{x1D712}_{m}$
varies in the range 200–3000
$\unicode[STIX]{x1D712}_{m}$
varies in the range 200–3000
![]() $\text{cm}^{-1}$
(Niederer et al.
Reference Niederer, Kerfoot, Benson, Bernabeu, Bernus, Bradley, Cherry, Clayton, Fenton and Garny2011, Potse et al.
Reference Potse, Dubé, Richer, Vinet and Gulrajani2006), whereas for the Purkinje network, a measurement in a pig heart gives
$\text{cm}^{-1}$
(Niederer et al.
Reference Niederer, Kerfoot, Benson, Bernabeu, Bernus, Bradley, Cherry, Clayton, Fenton and Garny2011, Potse et al.
Reference Potse, Dubé, Richer, Vinet and Gulrajani2006), whereas for the Purkinje network, a measurement in a pig heart gives
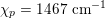 $\unicode[STIX]{x1D712}_{p}=1467~\text{cm}^{-1}$
(Stankovičová et al.
Reference Stankovičová, Bito, Heinzel, Mubagwa and Sipido2003). In the myocardium, we need to distinguish between conductivity along the fibre direction (index
$\unicode[STIX]{x1D712}_{p}=1467~\text{cm}^{-1}$
(Stankovičová et al.
Reference Stankovičová, Bito, Heinzel, Mubagwa and Sipido2003). In the myocardium, we need to distinguish between conductivity along the fibre direction (index
![]() $f$
) and conductivity in the direction of sheets (index
$f$
) and conductivity in the direction of sheets (index
![]() $s$
). Sometimes, a third direction (orthogonal to sheets) is also considered (if this is the case we will use the index
$s$
). Sometimes, a third direction (orthogonal to sheets) is also considered (if this is the case we will use the index
![]() $n$
). Moreover, with the bidomain model in mind, we also distinguish between the intra-cellular (index
$n$
). Moreover, with the bidomain model in mind, we also distinguish between the intra-cellular (index
![]() $i$
) and extra-cellular (index
$i$
) and extra-cellular (index
![]() $e$
) conductivities. Following Roth (Reference Roth1997), acceptable ranges used in the numerical experiments are
$e$
) conductivities. Following Roth (Reference Roth1997), acceptable ranges used in the numerical experiments are
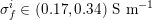 $\unicode[STIX]{x1D70E}_{f}^{i}\in (0.17,0.34)~\text{S}~\text{m}^{-1}$
,
$\unicode[STIX]{x1D70E}_{f}^{i}\in (0.17,0.34)~\text{S}~\text{m}^{-1}$
,
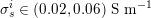 $\unicode[STIX]{x1D70E}_{s}^{i}\in (0.02,0.06)~\text{S}~\text{m}^{-1}$
,
$\unicode[STIX]{x1D70E}_{s}^{i}\in (0.02,0.06)~\text{S}~\text{m}^{-1}$
,
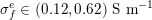 $\unicode[STIX]{x1D70E}_{f}^{e}\in (0.12,0.62)~\text{S}~\text{m}^{-1}$
,
$\unicode[STIX]{x1D70E}_{f}^{e}\in (0.12,0.62)~\text{S}~\text{m}^{-1}$
,
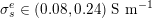 $\unicode[STIX]{x1D70E}_{s}^{e}\in (0.08,0.24)~\text{S}~\text{m}^{-1}$
.
$\unicode[STIX]{x1D70E}_{s}^{e}\in (0.08,0.24)~\text{S}~\text{m}^{-1}$
.
Another classical model used to describe the activation of Purkinje and muscle cells is provided by the eikonal equation (see Section 7.1). In this case, one needs to prescribe the conduction velocity
![]() $V$
explicitly, unlike the monodomain and bidomain models where this is determined by the conductivity and the membrane capacitance. Acceptable ranges of values of the conduction velocity are
$V$
explicitly, unlike the monodomain and bidomain models where this is determined by the conductivity and the membrane capacitance. Acceptable ranges of values of the conduction velocity are
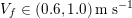 $V_{f}\in (0.6,1.0)\,\text{m}~\text{s}^{-1}$
(Kerckoffs et al.
Reference Kerckoffs, Faris, Boveenderd, Prinzen, Smits and Arts2003),
$V_{f}\in (0.6,1.0)\,\text{m}~\text{s}^{-1}$
(Kerckoffs et al.
Reference Kerckoffs, Faris, Boveenderd, Prinzen, Smits and Arts2003),
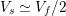 $V_{s}\simeq V_{f}/2$
(Frazier et al.
Reference Frazier, Krassowska, Chen, Wolf, Danieley, Smith and Ideker1988),
$V_{s}\simeq V_{f}/2$
(Frazier et al.
Reference Frazier, Krassowska, Chen, Wolf, Danieley, Smith and Ideker1988),
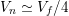 $V_{n}\simeq V_{f}/4$
(Clayton et al.
Reference Clayton, Bernus, Cherry, Dierckx, Fenton, Mirabella, Panfilov, Sachse, Seemann and Zhang2011), and
$V_{n}\simeq V_{f}/4$
(Clayton et al.
Reference Clayton, Bernus, Cherry, Dierckx, Fenton, Mirabella, Panfilov, Sachse, Seemann and Zhang2011), and
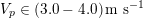 $V_{p}\in (3.0-4.0)\,\text{m}~\text{s}^{-1}$
(Iaizzo Reference Iaizzo2009), where again index
$V_{p}\in (3.0-4.0)\,\text{m}~\text{s}^{-1}$
(Iaizzo Reference Iaizzo2009), where again index
![]() $f$
refers to the direction along the fibres in the muscle region,
$f$
refers to the direction along the fibres in the muscle region,
![]() $s$
to the direction along sheets, and
$s$
to the direction along sheets, and
![]() $p$
to the Purkinje network.
$p$
to the Purkinje network.
These electrical data are barely measurable in vivo, so subject-specific measurements are not usually available. Nevertheless, the use of extra data, such as the activation time at the endocardium provided by the NavX system, could be used to estimate some of these parameters by solving a suitable inverse problem; see e.g. Sermesant et al. (Reference Sermesant, Chabiniok, Chinchapatnam, Mansi, Billet, Moireau, Peyrat, Wong, Relan, Rhode, Ginks, Lambiase, Delingette, Sorine, Rinaldi, Chapelle, Razavi and Ayache2012) and Vergara et al. (Reference Vergara, Palamara, Catanzariti, Nobile, Faggiano, Pangrazzi, Centonze, Maines, Quarteroni and Vergara2014) for the case of the Purkinje network.
The parameters involved in the cardiac mechanical model depend on the chosen constitutive law. In general, linearization of the stress–strain curves gives the following values for the corresponding time-varying Young’s modulus
![]() $E$
(Rossi Reference Rossi2014): during a traction/compression test along the fibre direction, we have
$E$
(Rossi Reference Rossi2014): during a traction/compression test along the fibre direction, we have
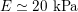 $E\simeq 20~\text{kPa}$
during traction at small deformation and during compression, and
$E\simeq 20~\text{kPa}$
during traction at small deformation and during compression, and
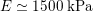 $E\simeq 1500~\text{kPa}$
during traction for deformation of about
$E\simeq 1500~\text{kPa}$
during traction for deformation of about
![]() $15\%$
; during traction the material behaves as transversally isotropic, so the stiffness in the two tangential directions (along sheets and orthogonal to fibres and sheets) is the same, whereas during compression the stiffness in the direction of the sheets is higher than that in the direction orthogonal to fibres and sheets. For the Poisson modulus, a value of
$15\%$
; during traction the material behaves as transversally isotropic, so the stiffness in the two tangential directions (along sheets and orthogonal to fibres and sheets) is the same, whereas during compression the stiffness in the direction of the sheets is higher than that in the direction orthogonal to fibres and sheets. For the Poisson modulus, a value of
![]() $0.45$
is usually considered.
$0.45$
is usually considered.
Regarding the aortic valve leaflets, measurements in dogs exhibited low stiffness during systole (
 $\simeq 240~\text{kPa}$
) and increased stiffness during diastole (
$\simeq 240~\text{kPa}$
) and increased stiffness during diastole (
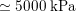 $\simeq 5000~\text{kPa}$
). For the mitral valve, different stiffness behaviour is observed for the two leaflets (anterior and posterior). In particular, Kunzelman et al. (Reference Kunzelman, Cochran, Chuong, Ring and Eberhart1993) propose the following values for Young’s modulus: for the anterior leaflet,
$\simeq 5000~\text{kPa}$
). For the mitral valve, different stiffness behaviour is observed for the two leaflets (anterior and posterior). In particular, Kunzelman et al. (Reference Kunzelman, Cochran, Chuong, Ring and Eberhart1993) propose the following values for Young’s modulus: for the anterior leaflet,
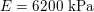 $E=6200~\text{kPa}$
and
$E=6200~\text{kPa}$
and
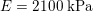 $E=2100~\text{kPa}$
in the directions parallel and perpendicular to the annulus, respectively, and for the posterior leaflet,
$E=2100~\text{kPa}$
in the directions parallel and perpendicular to the annulus, respectively, and for the posterior leaflet,
 $E=2300~\text{kPa}$
and
$E=2300~\text{kPa}$
and
 $E=1900~\text{kPa}$
, respectively.
$E=1900~\text{kPa}$
, respectively.
Blood in the heart exhibits the same behaviour as in the circulatory systems, so its parameters (density and viscosity) are taken in the ranges reported in Section 3.3.
7 Modelling the heart
In this section we discuss the main mathematical models introduced so far to describe heart function and the related numerical strategies developed for their solution. In particular, Section 7.1 is devoted to the electrical propagation, Section 7.2 to the cardiac mechanics and electromechanical coupling, Section 7.3 to the ventricular fluid dynamics, Section 7.4 to the valve modelling and its interaction with blood fluid dynamics, and finally Section 7.5 to their integration.
7.1 Cardiac electrical activity
7.1.1 The bidomain model
As observed in Section 5.3, the electrical activation of the heart is the result of two processes: at the microscopic scales, the generation of ionic currents through the cellular membrane producing a local action potential, and at the macroscopic scales, the travelling of the action potential from cell to cell allowed by the presence of the gap junctions. The former is a discrete process, in the sense that there is a delay between the depolarization of a cardiomyocyte and its neighbours, whereas the latter can be assimilated to a smooth process (Durrer et al. Reference Durrer, van Dam, Freud, Janse, Meijler and Arzbaecher1970).

Figure 7.1. Electrical circuit for the sequence of two cardiac cells. Each consists of a capacitor and a series of resistances, one for each ionic current (here only sodium and potassium ionic channels are depicted). In the intracellular region, two adjacent cells are connected by a resistance representing a gap junction. However, the latter is not explicitly modelled at the macroscopic scales: instead its effect is hidden in the conductivity tensor (see the text).
At the macroscopic level, the propagation of the potentials is described by means of partial differential equations, suitably coupled with ordinary differential equations modelling the ionic currents in the cells. In particular, the single membrane cell can be modelled as a capacitor separating charges that accumulate at its intracellular and extracellular surfaces. Moreover, as observed in Section 5, ionic currents cross the membrane through channels which open and close during excitation. A suitable model can therefore be expressed via the simple electric circuit depicted in Figure 7.1, for which
 $$\begin{eqnarray}I_{m}=\unicode[STIX]{x1D712}_{m}\biggl(C_{m}\frac{\unicode[STIX]{x2202}V_{m}}{\unicode[STIX]{x2202}t}+I_{\mathit{ion}}\biggr),\end{eqnarray}$$
$$\begin{eqnarray}I_{m}=\unicode[STIX]{x1D712}_{m}\biggl(C_{m}\frac{\unicode[STIX]{x2202}V_{m}}{\unicode[STIX]{x2202}t}+I_{\mathit{ion}}\biggr),\end{eqnarray}$$
where
![]() $I_{m}$
is the membrane current per unit volume,
$I_{m}$
is the membrane current per unit volume,
![]() $C_{m}$
is the membrane capacitance,
$C_{m}$
is the membrane capacitance,
![]() $\unicode[STIX]{x1D712}_{m}$
is the surface area-to-volume ratio (see Section 6.3 for a quantification of the latter two),
$\unicode[STIX]{x1D712}_{m}$
is the surface area-to-volume ratio (see Section 6.3 for a quantification of the latter two),
 $V_{m}(t,\boldsymbol{x})$
is the trans-membrane potential, and
$V_{m}(t,\boldsymbol{x})$
is the trans-membrane potential, and
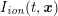 $I_{\mathit{ion}}(t,\boldsymbol{x})$
are the ionic currents. Due to the conservation of current and charge, this current should equal the divergence of both the intracellular and extracellular current fluxes
$I_{\mathit{ion}}(t,\boldsymbol{x})$
are the ionic currents. Due to the conservation of current and charge, this current should equal the divergence of both the intracellular and extracellular current fluxes
![]() $\boldsymbol{j}_{i}$
and
$\boldsymbol{j}_{i}$
and
![]() $\boldsymbol{j}_{e}$
:
$\boldsymbol{j}_{e}$
:
 $$\begin{eqnarray}\unicode[STIX]{x1D6FB}\cdot \boldsymbol{j}_{i}=-I_{m},\quad \unicode[STIX]{x1D6FB}\cdot \boldsymbol{j}_{e}=I_{m}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FB}\cdot \boldsymbol{j}_{i}=-I_{m},\quad \unicode[STIX]{x1D6FB}\cdot \boldsymbol{j}_{e}=I_{m}.\end{eqnarray}$$
Ohm’s law in the intracellular and extracellular regions gives
 $$\begin{eqnarray}\boldsymbol{j}_{i}=-\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D719}_{i},\quad \boldsymbol{j}_{e}=-\boldsymbol{\unicode[STIX]{x1D6F4}}_{e}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D719}_{e},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{j}_{i}=-\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D719}_{i},\quad \boldsymbol{j}_{e}=-\boldsymbol{\unicode[STIX]{x1D6F4}}_{e}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D719}_{e},\end{eqnarray}$$
where
![]() $\boldsymbol{\unicode[STIX]{x1D6F4}}_{i},\boldsymbol{\unicode[STIX]{x1D6F4}}_{e}$
are the conductivity tensors and
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{i},\boldsymbol{\unicode[STIX]{x1D6F4}}_{e}$
are the conductivity tensors and
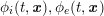 $\unicode[STIX]{x1D719}_{i}(t,\boldsymbol{x}),\unicode[STIX]{x1D719}_{e}(t,\boldsymbol{x})$
are the intracellular and extracellular potentials, so that
$\unicode[STIX]{x1D719}_{i}(t,\boldsymbol{x}),\unicode[STIX]{x1D719}_{e}(t,\boldsymbol{x})$
are the intracellular and extracellular potentials, so that
 $$\begin{eqnarray}V_{m}=\unicode[STIX]{x1D719}_{i}-\unicode[STIX]{x1D719}_{e}.\end{eqnarray}$$
$$\begin{eqnarray}V_{m}=\unicode[STIX]{x1D719}_{i}-\unicode[STIX]{x1D719}_{e}.\end{eqnarray}$$
Note that, due to the anisotropy of the cardiac tissue induced by the presence of fibres and sheets, each conductivity tensor is in general expressed in terms of three scalar quantities representing the conductivities along the fibre direction
![]() $\boldsymbol{a}_{f}(\boldsymbol{x})$
, the direction
$\boldsymbol{a}_{f}(\boldsymbol{x})$
, the direction
![]() $\boldsymbol{a}_{s}(\boldsymbol{x})$
orthogonal to
$\boldsymbol{a}_{s}(\boldsymbol{x})$
orthogonal to
![]() $\boldsymbol{a}_{f}$
and tangential to sheets, and the direction
$\boldsymbol{a}_{f}$
and tangential to sheets, and the direction
![]() $\boldsymbol{a}_{n}(\boldsymbol{x})$
orthogonal to sheets, that is,
$\boldsymbol{a}_{n}(\boldsymbol{x})$
orthogonal to sheets, that is,
 $$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D6F4}}_{\unicode[STIX]{x1D6FD}}=\unicode[STIX]{x1D70E}_{f}^{\unicode[STIX]{x1D6FD}}\boldsymbol{a}_{f}\boldsymbol{a}_{f}^{T}+\unicode[STIX]{x1D70E}_{s}^{\unicode[STIX]{x1D6FD}}\boldsymbol{a}_{s}\boldsymbol{a}_{s}^{T}+\unicode[STIX]{x1D70E}_{n}^{\unicode[STIX]{x1D6FD}}\boldsymbol{a}_{n}\boldsymbol{a}_{n}^{T},\quad \unicode[STIX]{x1D6FD}=i,e.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D6F4}}_{\unicode[STIX]{x1D6FD}}=\unicode[STIX]{x1D70E}_{f}^{\unicode[STIX]{x1D6FD}}\boldsymbol{a}_{f}\boldsymbol{a}_{f}^{T}+\unicode[STIX]{x1D70E}_{s}^{\unicode[STIX]{x1D6FD}}\boldsymbol{a}_{s}\boldsymbol{a}_{s}^{T}+\unicode[STIX]{x1D70E}_{n}^{\unicode[STIX]{x1D6FD}}\boldsymbol{a}_{n}\boldsymbol{a}_{n}^{T},\quad \unicode[STIX]{x1D6FD}=i,e.\end{eqnarray}$$
Putting together all the above equations and using a homogenization procedure (see e.g. Colli Franzone et al. Reference Colli Franzone, Pavarino and Scacchi2014 for a rigorous derivation), we obtain for each
![]() $t>0$
the following system of two partial differential equations called the parabolic–parabolic (PP) formulation of the bidomain equations:
$t>0$
the following system of two partial differential equations called the parabolic–parabolic (PP) formulation of the bidomain equations:
 $$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D712}_{m}C_{m}\frac{\unicode[STIX]{x2202}V_{m}}{\unicode[STIX]{x2202}t}-\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D719}_{i})+\unicode[STIX]{x1D712}_{m}I_{\mathit{ion}}=I_{i}^{\mathit{ext}} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D712}_{m}C_{m}\frac{\unicode[STIX]{x2202}V_{m}}{\unicode[STIX]{x2202}t}-\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D719}_{i})+\unicode[STIX]{x1D712}_{m}I_{\mathit{ion}}=I_{i}^{\mathit{ext}} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle -\unicode[STIX]{x1D712}_{m}C_{m}\frac{\unicode[STIX]{x2202}V_{m}}{\unicode[STIX]{x2202}t}-\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{\unicode[STIX]{x1D6F4}}_{e}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D719}_{e})-\unicode[STIX]{x1D712}_{m}I_{\mathit{ion}}=-I_{e}^{\mathit{ext}} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle -\unicode[STIX]{x1D712}_{m}C_{m}\frac{\unicode[STIX]{x2202}V_{m}}{\unicode[STIX]{x2202}t}-\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{\unicode[STIX]{x1D6F4}}_{e}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D719}_{e})-\unicode[STIX]{x1D712}_{m}I_{\mathit{ion}}=-I_{e}^{\mathit{ext}} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
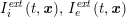 $I_{i}^{\mathit{ext}}(t,\boldsymbol{x}),\,I_{e}^{\mathit{ext}}(t,\boldsymbol{x})$
are applied currents per unit volume.
$I_{i}^{\mathit{ext}}(t,\boldsymbol{x}),\,I_{e}^{\mathit{ext}}(t,\boldsymbol{x})$
are applied currents per unit volume.
Thanks to (7.1),
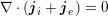 $\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{j}_{i}+\boldsymbol{j}_{e})=0$
; thus, using (7.2) and (7.3), we obtain the following parabolic–elliptic (PE) formulation of the bidomain equations:
$\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{j}_{i}+\boldsymbol{j}_{e})=0$
; thus, using (7.2) and (7.3), we obtain the following parabolic–elliptic (PE) formulation of the bidomain equations:
 $$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D712}_{m}C_{m}\frac{\unicode[STIX]{x2202}V_{m}}{\unicode[STIX]{x2202}t}-\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}(\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D719}_{e}+\unicode[STIX]{x1D6FB}V_{m}))+\unicode[STIX]{x1D712}_{m}I_{\mathit{ion}}=I_{i}^{\mathit{ext}} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D712}_{m}C_{m}\frac{\unicode[STIX]{x2202}V_{m}}{\unicode[STIX]{x2202}t}-\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}(\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D719}_{e}+\unicode[STIX]{x1D6FB}V_{m}))+\unicode[STIX]{x1D712}_{m}I_{\mathit{ion}}=I_{i}^{\mathit{ext}} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle -\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}\unicode[STIX]{x1D6FB}V_{m})-\unicode[STIX]{x1D6FB}\cdot ((\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}+\boldsymbol{\unicode[STIX]{x1D6F4}}_{e})\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D719}_{e})=I_{i}^{\mathit{ext}}-I_{e}^{\mathit{ext}} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle -\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}\unicode[STIX]{x1D6FB}V_{m})-\unicode[STIX]{x1D6FB}\cdot ((\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}+\boldsymbol{\unicode[STIX]{x1D6F4}}_{e})\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D719}_{e})=I_{i}^{\mathit{ext}}-I_{e}^{\mathit{ext}} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}.\end{eqnarray}$$
Due to the homogenization procedure, the effect of the gap junctions, which at the cellular level contributes to determining the current flux
![]() $\boldsymbol{j}_{i}$
, is hidden in the conductivity tensor
$\boldsymbol{j}_{i}$
, is hidden in the conductivity tensor
![]() $\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}$
. We also notice that both bidomain problems (7.5) and (7.6) hold in the entire computational domain
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}$
. We also notice that both bidomain problems (7.5) and (7.6) hold in the entire computational domain
![]() $\unicode[STIX]{x1D6FA}_{\mathit{mus}}$
given by the union of the myocardium with the endocardium and epicardium: see Figures 6.1 and 7.2. Indeed, again because of the homogenization procedure, no geometric distinction is made between the intracellular and extracellular regions, even if their different functionality is maintained in the bidomain models.
$\unicode[STIX]{x1D6FA}_{\mathit{mus}}$
given by the union of the myocardium with the endocardium and epicardium: see Figures 6.1 and 7.2. Indeed, again because of the homogenization procedure, no geometric distinction is made between the intracellular and extracellular regions, even if their different functionality is maintained in the bidomain models.

Figure 7.2. (a) Left ventricular myocardial domain obtained by the cut at the base (corresponding to
![]() $\unicode[STIX]{x1D6F4}_{b}$
), and (b) corresponding fluid cavity domain.
$\unicode[STIX]{x1D6F4}_{b}$
), and (b) corresponding fluid cavity domain.
7.1.2 Cardiac cell models
In order to close equations (7.5) and (7.6), we need to provide a model for the ionic current
![]() $I_{\mathit{ion}}$
. In what follows we briefly describe three families of models, featuring different levels of complexity and accuracy.
$I_{\mathit{ion}}$
. In what follows we briefly describe three families of models, featuring different levels of complexity and accuracy.
The first family, the so-called reduced ionic models, only provide a description of the action potential and disregard sub-cellular processes:
 $$\begin{eqnarray}\displaystyle & \displaystyle I_{\mathit{ion}}=f(V_{m},\boldsymbol{w}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle I_{\mathit{ion}}=f(V_{m},\boldsymbol{w}), & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{w}}{\unicode[STIX]{x2202}t}=\boldsymbol{g}_{w}(V_{m},\boldsymbol{w}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{w}}{\unicode[STIX]{x2202}t}=\boldsymbol{g}_{w}(V_{m},\boldsymbol{w}), & \displaystyle\end{eqnarray}$$
 $\boldsymbol{w}:[0,T]\times \unicode[STIX]{x1D6FA}_{\mathit{mus}}\rightarrow \mathbb{R}^{M}$
collects the so-called gating variables which represent the percentage of open channels per unit area of the membrane. The most celebrated reduced model for ventricular cells is the FitzHugh–Nagumo model (FitzHugh Reference Fitzhugh1961), where
$\boldsymbol{w}:[0,T]\times \unicode[STIX]{x1D6FA}_{\mathit{mus}}\rightarrow \mathbb{R}^{M}$
collects the so-called gating variables which represent the percentage of open channels per unit area of the membrane. The most celebrated reduced model for ventricular cells is the FitzHugh–Nagumo model (FitzHugh Reference Fitzhugh1961), where
 $f(V_{m},w)=-kV_{m}(V_{m}-a)(V_{m}-1)-w$
and
$f(V_{m},w)=-kV_{m}(V_{m}-a)(V_{m}-1)-w$
and
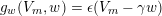 $g_{w}(V_{m},w)=\unicode[STIX]{x1D716}(V_{m}-\unicode[STIX]{x1D6FE}w)$
, for suitable constant parameters
$g_{w}(V_{m},w)=\unicode[STIX]{x1D716}(V_{m}-\unicode[STIX]{x1D6FE}w)$
, for suitable constant parameters
The second family of ventricular cell models we consider is that of the so-called first-generation models. Unlike reduced models, which express the ionic current by means of the sole function
![]() $f$
, they allow explicit description of the kinetics of different ionic currents by using several gating variables. They are given by
$f$
, they allow explicit description of the kinetics of different ionic currents by using several gating variables. They are given by
 $$\begin{eqnarray}\displaystyle I_{\mathit{ion}}=\mathop{\sum }_{k=1}^{N}I_{k}(V_{m},\boldsymbol{w}),\quad I_{k}=G_{k}\biggl(\mathop{\prod }_{j=1}^{M}w_{j}^{p_{j_{k}}}\biggr)(V_{m}-V_{k}),\quad \frac{\unicode[STIX]{x2202}\boldsymbol{w}}{\unicode[STIX]{x2202}t}=\boldsymbol{g}_{w}(V_{m},\boldsymbol{w}), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{\mathit{ion}}=\mathop{\sum }_{k=1}^{N}I_{k}(V_{m},\boldsymbol{w}),\quad I_{k}=G_{k}\biggl(\mathop{\prod }_{j=1}^{M}w_{j}^{p_{j_{k}}}\biggr)(V_{m}-V_{k}),\quad \frac{\unicode[STIX]{x2202}\boldsymbol{w}}{\unicode[STIX]{x2202}t}=\boldsymbol{g}_{w}(V_{m},\boldsymbol{w}), & & \displaystyle \nonumber\end{eqnarray}$$
where
![]() $N$
is the total number of ionic currents,
$N$
is the total number of ionic currents,
![]() $M$
is the total number of gating variables,
$M$
is the total number of gating variables,
![]() $V_{k}$
is the Nernst potential of the
$V_{k}$
is the Nernst potential of the
![]() $k$
th ion (a constant value corresponding to the thermodynamic equilibrium of the ion at hand),
$k$
th ion (a constant value corresponding to the thermodynamic equilibrium of the ion at hand),
![]() $I_{k}$
is the current related to the
$I_{k}$
is the current related to the
![]() $k$
th ion,
$k$
th ion,
![]() $p_{j_{k}}$
accounts for the influence of the
$p_{j_{k}}$
accounts for the influence of the
![]() $j$
th gating variable on the
$j$
th gating variable on the
![]() $k$
th ionic current (possibly vanishing) and
$k$
th ionic current (possibly vanishing) and
![]() $G_{k}$
is the maximal conductance of the
$G_{k}$
is the maximal conductance of the
![]() $k$
th ion. The
$k$
th ion. The
![]() $M$
components of
$M$
components of
![]() $\boldsymbol{g}$
usually have the expression
$\boldsymbol{g}$
usually have the expression
 $$\begin{eqnarray}g_{w,j}=(w_{j}^{\infty }(V_{m})-w_{j})/\unicode[STIX]{x1D70F}_{j}(V_{m}),\end{eqnarray}$$
$$\begin{eqnarray}g_{w,j}=(w_{j}^{\infty }(V_{m})-w_{j})/\unicode[STIX]{x1D70F}_{j}(V_{m}),\end{eqnarray}$$
where
![]() $w_{j}^{\infty }$
is the equilibrium state and
$w_{j}^{\infty }$
is the equilibrium state and
![]() $\unicode[STIX]{x1D70F}_{j}$
the characteristic time constant. The most famous model of this family, the Hodgkin–Huxley (HH) model (Hodgkin and Huxley Reference Hodgkin and Huxley1952), depends on three ionic currents, namely the sodium, potassium and leakage currents, and three gating variables:
$\unicode[STIX]{x1D70F}_{j}$
the characteristic time constant. The most famous model of this family, the Hodgkin–Huxley (HH) model (Hodgkin and Huxley Reference Hodgkin and Huxley1952), depends on three ionic currents, namely the sodium, potassium and leakage currents, and three gating variables:
 $$\begin{eqnarray}I_{Na}=G_{Na}w_{1}^{3}w_{2}(V_{m}-V_{Na}),\quad I_{K}=G_{K}w_{3}^{4}(V_{m}-V_{K}),\quad I_{L}=G_{L}(V_{M}-V_{L}).\end{eqnarray}$$
$$\begin{eqnarray}I_{Na}=G_{Na}w_{1}^{3}w_{2}(V_{m}-V_{Na}),\quad I_{K}=G_{K}w_{3}^{4}(V_{m}-V_{K}),\quad I_{L}=G_{L}(V_{M}-V_{L}).\end{eqnarray}$$
Although introduced to describe the action potentials in nerves, the HH model inspired all the following models introduced specifically for the ventricle. Among these, we cite the Beeler–Reuter model (Beeler and Reuter Reference Beeler and Reuter1977), the Luo–Rudy I model (Luo and Rudy Reference Luo and Rudy1991) and the ten Tusscher–Panfilov model (ten Tusscher and Panfilov Reference ten Tusscher and Panfilov2006). These models have been widely used to study specific features of the ventricular electrical activation, such as re-entry and fibrillation (Xie et al. Reference Xie, Qu, Yang, Baher, Weiss and Garfinkel2004).
Finally, we mention the family of second-generation ventricular cell models, such as the Luo–Rudy dynamic model (Luo and Rudy Reference Luo and Rudy1994a
, Reference Luo and Rudy1994b
), which, unlike first-generation models, provide a detailed description of ion concentration variables
![]() $\boldsymbol{c}$
and of many processes allowing for the study of channelopathies and drug action, for example. However, due to their increased complexity, the computational time required is huge for a complete heart model, and tuning of parameters is often very demanding. We refer to Clayton and Panfilov (Reference Clayton and Panfilov2008) for a discussion of second-generation models and Rudy and Silva (Reference Rudy and Silva2006) for a general review of cardiac cell models.
$\boldsymbol{c}$
and of many processes allowing for the study of channelopathies and drug action, for example. However, due to their increased complexity, the computational time required is huge for a complete heart model, and tuning of parameters is often very demanding. We refer to Clayton and Panfilov (Reference Clayton and Panfilov2008) for a discussion of second-generation models and Rudy and Silva (Reference Rudy and Silva2006) for a general review of cardiac cell models.
Although most research has focused on ventricular cell models like those mentioned above, specific models have also been introduced for the atrial cells (e.g. Hilgemann and Noble Reference Hilgemann and Noble1987) and sinoatrial node cells (e.g. Yanagihara, Noma and Irisawa Reference Yanagihara, Noma and Irisawa1980).
All the cardiac cell models belonging to the three families described above, used in combination with the bidomain problem (7.5) or (7.6), lead to a system of two PDEs coupled with two systems of ODEs, that is, the equations for the gating variables and ion concentrations at each point
![]() $\boldsymbol{x}$
. The general form of this coupled problem is as follows (we only describe the PP case in detail). At each time
$\boldsymbol{x}$
. The general form of this coupled problem is as follows (we only describe the PP case in detail). At each time
![]() $t>0$
, find the potentials
$t>0$
, find the potentials
![]() $V_{M},\,\unicode[STIX]{x1D719}_{i}$
and
$V_{M},\,\unicode[STIX]{x1D719}_{i}$
and
![]() $\unicode[STIX]{x1D719}_{e}$
, the gating variable
$\unicode[STIX]{x1D719}_{e}$
, the gating variable
![]() $\boldsymbol{w}$
and the ion concentrations
$\boldsymbol{w}$
and the ion concentrations
![]() $\boldsymbol{c}$
such that
$\boldsymbol{c}$
such that
 $$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D712}_{m}C_{m}\frac{\unicode[STIX]{x2202}V_{m}}{\unicode[STIX]{x2202}t}-\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D719}_{i})+\unicode[STIX]{x1D712}_{m}I_{\mathit{ion}}(V_{m},\boldsymbol{w},\boldsymbol{c})=I_{i}^{\mathit{ext}} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D712}_{m}C_{m}\frac{\unicode[STIX]{x2202}V_{m}}{\unicode[STIX]{x2202}t}-\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D719}_{i})+\unicode[STIX]{x1D712}_{m}I_{\mathit{ion}}(V_{m},\boldsymbol{w},\boldsymbol{c})=I_{i}^{\mathit{ext}} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle -\unicode[STIX]{x1D712}_{m}C_{m}\frac{\unicode[STIX]{x2202}V_{m}}{\unicode[STIX]{x2202}t}-\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{\unicode[STIX]{x1D6F4}}_{e}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D719}_{e})-\unicode[STIX]{x1D712}_{m}I_{\mathit{ion}}(V_{m},\boldsymbol{w},\boldsymbol{c}) & & \displaystyle \nonumber\\ \displaystyle \qquad =-I_{e}^{\mathit{ext}} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle -\unicode[STIX]{x1D712}_{m}C_{m}\frac{\unicode[STIX]{x2202}V_{m}}{\unicode[STIX]{x2202}t}-\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{\unicode[STIX]{x1D6F4}}_{e}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D719}_{e})-\unicode[STIX]{x1D712}_{m}I_{\mathit{ion}}(V_{m},\boldsymbol{w},\boldsymbol{c}) & & \displaystyle \nonumber\\ \displaystyle \qquad =-I_{e}^{\mathit{ext}} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle I_{\mathit{ion}}=\mathop{\sum }_{k=1}^{N}I_{k}(V_{m},\boldsymbol{w},\boldsymbol{c}) & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle I_{\mathit{ion}}=\mathop{\sum }_{k=1}^{N}I_{k}(V_{m},\boldsymbol{w},\boldsymbol{c}) & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle I_{k}=G_{k}\biggl(\mathop{\prod }_{j=1}^{M}w_{j}^{p_{j_{k}}}\biggr)(V_{m}-V_{k}(\boldsymbol{c})) & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle I_{k}=G_{k}\biggl(\mathop{\prod }_{j=1}^{M}w_{j}^{p_{j_{k}}}\biggr)(V_{m}-V_{k}(\boldsymbol{c})) & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{w}}{\unicode[STIX]{x2202}t}=\boldsymbol{g}_{w}(V_{m},\boldsymbol{w}) & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{w}}{\unicode[STIX]{x2202}t}=\boldsymbol{g}_{w}(V_{m},\boldsymbol{w}) & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{c}}{\unicode[STIX]{x2202}t}=\boldsymbol{g}_{c}(V_{m},\boldsymbol{w},\boldsymbol{c}) & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{c}}{\unicode[STIX]{x2202}t}=\boldsymbol{g}_{c}(V_{m},\boldsymbol{w},\boldsymbol{c}) & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
 $\boldsymbol{c}:[0,T]\times \unicode[STIX]{x1D6FA}_{\mathit{mus}}\rightarrow \mathbb{R}^{S}$
collects the
$\boldsymbol{c}:[0,T]\times \unicode[STIX]{x1D6FA}_{\mathit{mus}}\rightarrow \mathbb{R}^{S}$
collects the
The ODE systems modelling the gating variables and the ionic concentration variables are in general stiff, since the Jacobians
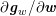 $\unicode[STIX]{x2202}\boldsymbol{g}_{w}/\unicode[STIX]{x2202}\boldsymbol{w}$
and
$\unicode[STIX]{x2202}\boldsymbol{g}_{w}/\unicode[STIX]{x2202}\boldsymbol{w}$
and
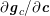 $\unicode[STIX]{x2202}\boldsymbol{g}_{c}/\unicode[STIX]{x2202}\boldsymbol{c}$
exhibit a wide range of eigenvalues.
$\unicode[STIX]{x2202}\boldsymbol{g}_{c}/\unicode[STIX]{x2202}\boldsymbol{c}$
exhibit a wide range of eigenvalues.
For each
![]() $t>0$
, the weak formulation of the bidomain model (7.9) together with homogeneous Neumann conditions and initial conditions (see Section 7.1.4) reads as follows. Given
$t>0$
, the weak formulation of the bidomain model (7.9) together with homogeneous Neumann conditions and initial conditions (see Section 7.1.4) reads as follows. Given
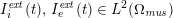 $I_{i}^{\mathit{ext}}(t),\,I_{e}^{\mathit{ext}}(t)\in L^{2}(\unicode[STIX]{x1D6FA}_{\mathit{mus}})$
, find
$I_{i}^{\mathit{ext}}(t),\,I_{e}^{\mathit{ext}}(t)\in L^{2}(\unicode[STIX]{x1D6FA}_{\mathit{mus}})$
, find
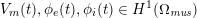 $V_{m}(t),\unicode[STIX]{x1D719}_{e}(t),\unicode[STIX]{x1D719}_{i}(t)\in H^{1}(\unicode[STIX]{x1D6FA}_{\mathit{mus}})$
,
$V_{m}(t),\unicode[STIX]{x1D719}_{e}(t),\unicode[STIX]{x1D719}_{i}(t)\in H^{1}(\unicode[STIX]{x1D6FA}_{\mathit{mus}})$
,
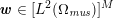 $\boldsymbol{w}\in [L^{2}(\unicode[STIX]{x1D6FA}_{\mathit{mus}})]^{M}$
and
$\boldsymbol{w}\in [L^{2}(\unicode[STIX]{x1D6FA}_{\mathit{mus}})]^{M}$
and
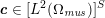 $\boldsymbol{c}\in [L^{2}(\unicode[STIX]{x1D6FA}_{\mathit{mus}})]^{S}$
such that
$\boldsymbol{c}\in [L^{2}(\unicode[STIX]{x1D6FA}_{\mathit{mus}})]^{S}$
such that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D712}_{m}C_{m}\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\frac{\unicode[STIX]{x2202}V_{m}}{\unicode[STIX]{x2202}t}z\text{d}\unicode[STIX]{x1D714}+\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D719}_{i}\cdot \unicode[STIX]{x1D6FB}z\text{d}\unicode[STIX]{x1D714}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \qquad +\,\unicode[STIX]{x1D712}_{m}\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}I_{\mathit{ion}}(V_{m},\boldsymbol{w},\boldsymbol{c})z\text{d}\unicode[STIX]{x1D714}=\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}I_{i}^{\mathit{ext}}z\text{d}\unicode[STIX]{x1D714},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D712}_{m}C_{m}\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\frac{\unicode[STIX]{x2202}V_{m}}{\unicode[STIX]{x2202}t}z\text{d}\unicode[STIX]{x1D714}+\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D719}_{i}\cdot \unicode[STIX]{x1D6FB}z\text{d}\unicode[STIX]{x1D714}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \qquad +\,\unicode[STIX]{x1D712}_{m}\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}I_{\mathit{ion}}(V_{m},\boldsymbol{w},\boldsymbol{c})z\text{d}\unicode[STIX]{x1D714}=\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}I_{i}^{\mathit{ext}}z\text{d}\unicode[STIX]{x1D714},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle -\unicode[STIX]{x1D712}_{m}C_{m}\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\frac{\unicode[STIX]{x2202}V_{m}}{\unicode[STIX]{x2202}t}z\text{d}\unicode[STIX]{x1D714}+\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\boldsymbol{\unicode[STIX]{x1D6F4}}_{e}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D719}_{e}\cdot \unicode[STIX]{x1D6FB}z\text{d}\unicode[STIX]{x1D714}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \qquad -\,\unicode[STIX]{x1D712}_{m}\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}I_{\mathit{ion}}(V_{m},\boldsymbol{w},\boldsymbol{c})z\text{d}\unicode[STIX]{x1D714}=-\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}I_{e}^{\mathit{ext}}z\text{d}\unicode[STIX]{x1D714},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle -\unicode[STIX]{x1D712}_{m}C_{m}\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\frac{\unicode[STIX]{x2202}V_{m}}{\unicode[STIX]{x2202}t}z\text{d}\unicode[STIX]{x1D714}+\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\boldsymbol{\unicode[STIX]{x1D6F4}}_{e}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D719}_{e}\cdot \unicode[STIX]{x1D6FB}z\text{d}\unicode[STIX]{x1D714}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \qquad -\,\unicode[STIX]{x1D712}_{m}\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}I_{\mathit{ion}}(V_{m},\boldsymbol{w},\boldsymbol{c})z\text{d}\unicode[STIX]{x1D714}=-\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}I_{e}^{\mathit{ext}}z\text{d}\unicode[STIX]{x1D714},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\frac{\unicode[STIX]{x2202}\boldsymbol{w}}{\unicode[STIX]{x2202}t}\cdot \boldsymbol{y}\text{d}\unicode[STIX]{x1D714}=\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\boldsymbol{g}(V_{m},\boldsymbol{w})\cdot \boldsymbol{y}\text{d}\unicode[STIX]{x1D714},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\frac{\unicode[STIX]{x2202}\boldsymbol{w}}{\unicode[STIX]{x2202}t}\cdot \boldsymbol{y}\text{d}\unicode[STIX]{x1D714}=\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\boldsymbol{g}(V_{m},\boldsymbol{w})\cdot \boldsymbol{y}\text{d}\unicode[STIX]{x1D714},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\frac{\unicode[STIX]{x2202}\boldsymbol{c}}{\unicode[STIX]{x2202}t}\cdot \boldsymbol{\unicode[STIX]{x1D701}}\text{d}\unicode[STIX]{x1D714}=\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\boldsymbol{g}_{c}(V_{m},\boldsymbol{w},\boldsymbol{c})\cdot \boldsymbol{\unicode[STIX]{x1D701}}\text{d}\unicode[STIX]{x1D714},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\frac{\unicode[STIX]{x2202}\boldsymbol{c}}{\unicode[STIX]{x2202}t}\cdot \boldsymbol{\unicode[STIX]{x1D701}}\text{d}\unicode[STIX]{x1D714}=\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\boldsymbol{g}_{c}(V_{m},\boldsymbol{w},\boldsymbol{c})\cdot \boldsymbol{\unicode[STIX]{x1D701}}\text{d}\unicode[STIX]{x1D714},\end{eqnarray}$$
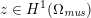 $z\in H^{1}(\unicode[STIX]{x1D6FA}_{\mathit{mus}})$
,
$z\in H^{1}(\unicode[STIX]{x1D6FA}_{\mathit{mus}})$
,
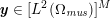 $\boldsymbol{y}\in [L^{2}(\unicode[STIX]{x1D6FA}_{\mathit{mus}})]^{M}$
and
$\boldsymbol{y}\in [L^{2}(\unicode[STIX]{x1D6FA}_{\mathit{mus}})]^{M}$
and
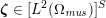 $\boldsymbol{\unicode[STIX]{x1D701}}\in [L^{2}(\unicode[STIX]{x1D6FA}_{\mathit{mus}})]^{S}$
, together with (7.9c
, 7.9d
).
$\boldsymbol{\unicode[STIX]{x1D701}}\in [L^{2}(\unicode[STIX]{x1D6FA}_{\mathit{mus}})]^{S}$
, together with (7.9c
, 7.9d
).
7.1.3 Reduced continuous models: the monodomain and eikonal equations
To reduce the complexity of the bidomain models (7.5) and (7.6), an assumption of proportionality between the intracellular and extracellular conductivities is introduced, that is,
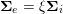 $\boldsymbol{\unicode[STIX]{x1D6F4}}_{e}=\unicode[STIX]{x1D709}\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}$
for a suitable constant
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{e}=\unicode[STIX]{x1D709}\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}$
for a suitable constant
![]() $\unicode[STIX]{x1D709}$
. Substituting this relation in (7.6b
), eliminating
$\unicode[STIX]{x1D709}$
. Substituting this relation in (7.6b
), eliminating
![]() $\boldsymbol{\unicode[STIX]{x1D6F4}}_{e}$
and substituting the corresponding relation for
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{e}$
and substituting the corresponding relation for
![]() $\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}$
in (7.6a
), we obtain the following monodomain equation. For each
$\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}$
in (7.6a
), we obtain the following monodomain equation. For each
![]() $t>0$
, find the trans-membrane potential
$t>0$
, find the trans-membrane potential
![]() $V_{m}$
such that
$V_{m}$
such that
 $$\begin{eqnarray}\unicode[STIX]{x1D712}_{m}C_{m}\frac{\unicode[STIX]{x2202}V_{m}}{\unicode[STIX]{x2202}t}-\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{\unicode[STIX]{x1D6F4}}\unicode[STIX]{x1D6FB}V_{m})+\unicode[STIX]{x1D712}_{m}I_{\mathit{ion}}=I^{\mathit{ext}}\quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D712}_{m}C_{m}\frac{\unicode[STIX]{x2202}V_{m}}{\unicode[STIX]{x2202}t}-\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{\unicode[STIX]{x1D6F4}}\unicode[STIX]{x1D6FB}V_{m})+\unicode[STIX]{x1D712}_{m}I_{\mathit{ion}}=I^{\mathit{ext}}\quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
where
 $$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D6F4}}=\frac{\unicode[STIX]{x1D709}}{1+\unicode[STIX]{x1D709}}\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D6F4}}=\frac{\unicode[STIX]{x1D709}}{1+\unicode[STIX]{x1D709}}\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}\end{eqnarray}$$
is the effective conductivity and
 $$\begin{eqnarray}I^{\mathit{ext}}=\displaystyle \frac{\unicode[STIX]{x1D709}I_{i}^{\mathit{ext}}+I_{e}^{\mathit{ext}}}{1+\unicode[STIX]{x1D709}}.\end{eqnarray}$$
$$\begin{eqnarray}I^{\mathit{ext}}=\displaystyle \frac{\unicode[STIX]{x1D709}I_{i}^{\mathit{ext}}+I_{e}^{\mathit{ext}}}{1+\unicode[STIX]{x1D709}}.\end{eqnarray}$$
Again, a ventricular cell model is needed to provide the ionic current
![]() $I_{\mathit{ion}}$
. The same models discussed above for the coupling with the bidomain problem are used in combination with the monodomain problem too. Once the trans-membrane potential
$I_{\mathit{ion}}$
. The same models discussed above for the coupling with the bidomain problem are used in combination with the monodomain problem too. Once the trans-membrane potential
![]() $V_{m}$
has been computed, the extracellular potential
$V_{m}$
has been computed, the extracellular potential
![]() $\unicode[STIX]{x1D719}_{e}$
could be computed as a postprocessing by solving the elliptic problem (7.6b
).
$\unicode[STIX]{x1D719}_{e}$
could be computed as a postprocessing by solving the elliptic problem (7.6b
).
For each
![]() $t>0$
, the weak formulation of the monodomain problem (7.11) together with homogeneous Neumann conditions and initial conditions (see Section 7.1.4) reads as follows. Given
$t>0$
, the weak formulation of the monodomain problem (7.11) together with homogeneous Neumann conditions and initial conditions (see Section 7.1.4) reads as follows. Given
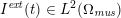 $I^{\mathit{ext}}(t)\in L^{2}(\unicode[STIX]{x1D6FA}_{\mathit{mus}})$
, find
$I^{\mathit{ext}}(t)\in L^{2}(\unicode[STIX]{x1D6FA}_{\mathit{mus}})$
, find
 $V_{m}(t)\in H^{1}(\unicode[STIX]{x1D6FA}_{\mathit{mus}})$
,
$V_{m}(t)\in H^{1}(\unicode[STIX]{x1D6FA}_{\mathit{mus}})$
,
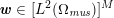 $\boldsymbol{w}\in [L^{2}(\unicode[STIX]{x1D6FA}_{\mathit{mus}})]^{M}$
and
$\boldsymbol{w}\in [L^{2}(\unicode[STIX]{x1D6FA}_{\mathit{mus}})]^{M}$
and
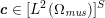 $\boldsymbol{c}\in [L^{2}(\unicode[STIX]{x1D6FA}_{\mathit{mus}})]^{S}$
such that
$\boldsymbol{c}\in [L^{2}(\unicode[STIX]{x1D6FA}_{\mathit{mus}})]^{S}$
such that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D712}_{m}C_{m}\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\frac{\unicode[STIX]{x2202}V_{m}}{\unicode[STIX]{x2202}t}z\text{d}\unicode[STIX]{x1D714}+\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\boldsymbol{\unicode[STIX]{x1D6F4}}\unicode[STIX]{x1D6FB}V_{m}\cdot \unicode[STIX]{x1D6FB}z\text{d}\unicode[STIX]{x1D714}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \qquad +\,\unicode[STIX]{x1D712}_{m}\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}I_{\mathit{ion}}(V_{m},\boldsymbol{w},\boldsymbol{c})z\text{d}\unicode[STIX]{x1D714}=\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}I^{\mathit{ext}}z\text{d}\unicode[STIX]{x1D714},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D712}_{m}C_{m}\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\frac{\unicode[STIX]{x2202}V_{m}}{\unicode[STIX]{x2202}t}z\text{d}\unicode[STIX]{x1D714}+\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\boldsymbol{\unicode[STIX]{x1D6F4}}\unicode[STIX]{x1D6FB}V_{m}\cdot \unicode[STIX]{x1D6FB}z\text{d}\unicode[STIX]{x1D714}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \qquad +\,\unicode[STIX]{x1D712}_{m}\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}I_{\mathit{ion}}(V_{m},\boldsymbol{w},\boldsymbol{c})z\text{d}\unicode[STIX]{x1D714}=\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}I^{\mathit{ext}}z\text{d}\unicode[STIX]{x1D714},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\frac{\unicode[STIX]{x2202}\boldsymbol{w}}{\unicode[STIX]{x2202}t}\cdot \boldsymbol{y}\text{d}\unicode[STIX]{x1D714}=\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\boldsymbol{g}(V_{m},\boldsymbol{w})\cdot \boldsymbol{y}\text{d}\unicode[STIX]{x1D714},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\frac{\unicode[STIX]{x2202}\boldsymbol{w}}{\unicode[STIX]{x2202}t}\cdot \boldsymbol{y}\text{d}\unicode[STIX]{x1D714}=\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\boldsymbol{g}(V_{m},\boldsymbol{w})\cdot \boldsymbol{y}\text{d}\unicode[STIX]{x1D714},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\frac{\unicode[STIX]{x2202}\boldsymbol{c}}{\unicode[STIX]{x2202}t}\cdot \boldsymbol{\unicode[STIX]{x1D701}}\text{d}\unicode[STIX]{x1D714}=\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\boldsymbol{g}_{c}(V_{m},\boldsymbol{w},\boldsymbol{c})\cdot \boldsymbol{\unicode[STIX]{x1D701}}\text{d}\unicode[STIX]{x1D714},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\frac{\unicode[STIX]{x2202}\boldsymbol{c}}{\unicode[STIX]{x2202}t}\cdot \boldsymbol{\unicode[STIX]{x1D701}}\text{d}\unicode[STIX]{x1D714}=\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\boldsymbol{g}_{c}(V_{m},\boldsymbol{w},\boldsymbol{c})\cdot \boldsymbol{\unicode[STIX]{x1D701}}\text{d}\unicode[STIX]{x1D714},\end{eqnarray}$$
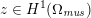 $z\in H^{1}(\unicode[STIX]{x1D6FA}_{\mathit{mus}})$
,
$z\in H^{1}(\unicode[STIX]{x1D6FA}_{\mathit{mus}})$
,
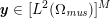 $\boldsymbol{y}\in [L^{2}(\unicode[STIX]{x1D6FA}_{\mathit{mus}})]^{M}$
and
$\boldsymbol{y}\in [L^{2}(\unicode[STIX]{x1D6FA}_{\mathit{mus}})]^{M}$
and
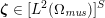 $\boldsymbol{\unicode[STIX]{x1D701}}\in [L^{2}(\unicode[STIX]{x1D6FA}_{\mathit{mus}})]^{S}$
, together with (7.9c
, 7.9d
).
$\boldsymbol{\unicode[STIX]{x1D701}}\in [L^{2}(\unicode[STIX]{x1D6FA}_{\mathit{mus}})]^{S}$
, together with (7.9c
, 7.9d
).
Although the hypothesis underlying the monodomain model, that is, the proportionality between the internal and external conductivities, is not physiological, as shown by experiment, in some cases this model provides a very accurate solution compared to the bidomain model. In particular, this is true when there is no injection of current in the extracellular region (Colli Franzone, Pavarino and Taccardi Reference Colli Franzone, Pavarino and Taccardi2005, Potse et al. Reference Potse, Dubé, Richer, Vinet and Gulrajani2006). In contrast, when an external current is injected such as in defibrillation, the monodomain solution is no longer accurate, and the bidomain model is mandatory since the unequal anisotropy is fundamental to successful description of these scenarios (Trayanova Reference Trayanova2006).
A further simplification is provided by the eikonal equation. Starting from the bidomain model coupled with a simplified representation of the ionic current, which does not consider any gating variable and allows for the description only of the depolarization phase, Colli Franzone, Guerri and Rovida (Reference Colli Franzone, Guerri and Rovida1990) derive the following eikonal-diffusion equation:
 $$\begin{eqnarray}c_{o}\sqrt{\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D713}\cdot \boldsymbol{M}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D713}}-\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{M}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D713})=1,\end{eqnarray}$$
$$\begin{eqnarray}c_{o}\sqrt{\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D713}\cdot \boldsymbol{M}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D713}}-\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{M}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D713})=1,\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D713}(\boldsymbol{x})$
is the unknown activation time (see Section 6.2),
$\unicode[STIX]{x1D713}(\boldsymbol{x})$
is the unknown activation time (see Section 6.2),
![]() $c_{o}$
denotes the velocity of the depolarization wave along the fibre direction for a planar wavefront, and
$c_{o}$
denotes the velocity of the depolarization wave along the fibre direction for a planar wavefront, and
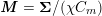 $\boldsymbol{M}=\boldsymbol{\unicode[STIX]{x1D6F4}}/(\unicode[STIX]{x1D712}C_{m})$
. A different derivation has been provided in Keener (Reference Keener1991), leading to the following eikonal-curvature equation:
$\boldsymbol{M}=\boldsymbol{\unicode[STIX]{x1D6F4}}/(\unicode[STIX]{x1D712}C_{m})$
. A different derivation has been provided in Keener (Reference Keener1991), leading to the following eikonal-curvature equation:
 $$\begin{eqnarray}c_{o}\sqrt{\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D713}\cdot \boldsymbol{M}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D713}}-\sqrt{\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D713}\cdot \boldsymbol{M}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D713}}\unicode[STIX]{x1D6FB}\cdot \biggl(\frac{\boldsymbol{M}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D713}}{\sqrt{\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D713}\cdot \boldsymbol{M}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D713}}}\biggr)=1.\end{eqnarray}$$
$$\begin{eqnarray}c_{o}\sqrt{\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D713}\cdot \boldsymbol{M}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D713}}-\sqrt{\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D713}\cdot \boldsymbol{M}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D713}}\unicode[STIX]{x1D6FB}\cdot \biggl(\frac{\boldsymbol{M}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D713}}{\sqrt{\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D713}\cdot \boldsymbol{M}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D713}}}\biggr)=1.\end{eqnarray}$$
These are both steady equations providing information on the activation of each cell. The contours of
![]() $\unicode[STIX]{x1D713}(\boldsymbol{x})$
give the position of the wavefront at time
$\unicode[STIX]{x1D713}(\boldsymbol{x})$
give the position of the wavefront at time
![]() $t=\unicode[STIX]{x1D713}$
. The eikonal-diffusive model (7.14) is an elliptic equation, where the propagation speed is influenced by the tissue surrounding the wavefront. Once the activation time
$t=\unicode[STIX]{x1D713}$
. The eikonal-diffusive model (7.14) is an elliptic equation, where the propagation speed is influenced by the tissue surrounding the wavefront. Once the activation time
![]() $\unicode[STIX]{x1D713}$
has been computed, it is possible to obtain an approximate value of the extracellular potential
$\unicode[STIX]{x1D713}$
has been computed, it is possible to obtain an approximate value of the extracellular potential
![]() $\unicode[STIX]{x1D719}_{e}$
by solving at each time step a suitable elliptic problem: see Colli Franzone and Guerri (Reference Colli Franzone and Guerri1993).
$\unicode[STIX]{x1D719}_{e}$
by solving at each time step a suitable elliptic problem: see Colli Franzone and Guerri (Reference Colli Franzone and Guerri1993).
In contrast, the eikonal-curvature model (7.15) is of parabolic type since the ‘diffusive’ term lacks the second derivative in the direction of propagation. This term is also proportional to an anisotropic generalization of the mean curvature (Tomlinson, Hunter and Pullan Reference Tomlinson, Hunter and Pullan2002). This implies that the propagation is faster when the wavefront is concave. This is in accordance with the diffusion of charge, which allows for faster depolarization in regions close to already depolarized tissues.
The eikonal equations are unsuitable for recovering the action potential and the ionic currents. However, they provide accurate results about the activation of cells even in complex scenarios such as front–front collision: see e.g. Colli Franzone and Guerri (Reference Colli Franzone and Guerri1993) for the eikonal-diffusive model.
The eikonal models are, however, very appealing from the computational point of view. First of all, they consist of a single steady PDE. Although non-linear, they do not require coupling with ODE systems. More importantly, the activation time, unlike the trans-membrane potential, does not feature any internal or boundary layer, so no special restriction on the mesh is needed in this case (see Section 6.1).
7.1.4 Boundary conditions and Purkinje network models
We discuss here the initial and boundary conditions of the problems introduced above. The bidomain and monodomain equations and the ODE systems for the gating variables and ionic concentrations need to be equipped with suitable initial conditions, that is,
 $$\begin{eqnarray}\displaystyle V_{m}|_{t=0}=V_{m,0},\quad \boldsymbol{w}|_{t=0}=\boldsymbol{w}_{0},\quad \boldsymbol{c}|_{t=0}=\boldsymbol{c}_{0}\quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle V_{m}|_{t=0}=V_{m,0},\quad \boldsymbol{w}|_{t=0}=\boldsymbol{w}_{0},\quad \boldsymbol{c}|_{t=0}=\boldsymbol{c}_{0}\quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}, & & \displaystyle \nonumber\end{eqnarray}$$
for given functions
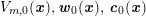 $V_{m,0}(\boldsymbol{x}),\boldsymbol{w}_{0}(\boldsymbol{x}),\,\boldsymbol{c}_{0}(\boldsymbol{x})$
.
$V_{m,0}(\boldsymbol{x}),\boldsymbol{w}_{0}(\boldsymbol{x}),\,\boldsymbol{c}_{0}(\boldsymbol{x})$
.
For the boundary conditions for the bidomain, monodomain and eikonal-diffusion problems, a homogeneous Neumann condition is commonly prescribed at the external surface
![]() $\unicode[STIX]{x1D6F4}_{\mathit{epi}}$
of the epicardium and, for a ventricular domain only, at the base
$\unicode[STIX]{x1D6F4}_{\mathit{epi}}$
of the epicardium and, for a ventricular domain only, at the base
![]() $\unicode[STIX]{x1D6F4}_{b}$
(see Figures 6.1 and 7.2(a)) to prescribe null outgoing current fluxes. In particular, the following conditions have to be prescribed on
$\unicode[STIX]{x1D6F4}_{b}$
(see Figures 6.1 and 7.2(a)) to prescribe null outgoing current fluxes. In particular, the following conditions have to be prescribed on
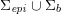 $\unicode[STIX]{x1D6F4}_{\mathit{epi}}\cup \unicode[STIX]{x1D6F4}_{b}$
:
$\unicode[STIX]{x1D6F4}_{\mathit{epi}}\cup \unicode[STIX]{x1D6F4}_{b}$
:
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}ll@{}}\displaystyle (\boldsymbol{\unicode[STIX]{x1D6F4}}_{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}})\cdot \boldsymbol{n}=0\quad \unicode[STIX]{x1D6FD}=i,e & \displaystyle \text{for PP (7.5)},\\ \begin{array}{@{}l@{}}(\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}\unicode[STIX]{x1D6FB}(V_{m}+\unicode[STIX]{x1D719}_{e}))\cdot \boldsymbol{n}=0\\ ((\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}+\boldsymbol{\unicode[STIX]{x1D6F4}}_{e})\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D719}_{e})\cdot \boldsymbol{n}+(\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}\unicode[STIX]{x1D6FB}V_{m})\cdot \boldsymbol{n}=0\end{array}\biggr\} & \displaystyle \text{for PE (7.6)},\\ \displaystyle (\boldsymbol{\unicode[STIX]{x1D6F4}}\unicode[STIX]{x1D6FB}V_{m})\cdot \boldsymbol{n}=0 & \displaystyle \text{for monodomain (7.11)},\\ \displaystyle (\boldsymbol{M}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D713})\cdot \boldsymbol{n}=0 & \displaystyle \text{for eikonal-diffusion (7.14)}.\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}ll@{}}\displaystyle (\boldsymbol{\unicode[STIX]{x1D6F4}}_{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D6FD}})\cdot \boldsymbol{n}=0\quad \unicode[STIX]{x1D6FD}=i,e & \displaystyle \text{for PP (7.5)},\\ \begin{array}{@{}l@{}}(\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}\unicode[STIX]{x1D6FB}(V_{m}+\unicode[STIX]{x1D719}_{e}))\cdot \boldsymbol{n}=0\\ ((\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}+\boldsymbol{\unicode[STIX]{x1D6F4}}_{e})\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D719}_{e})\cdot \boldsymbol{n}+(\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}\unicode[STIX]{x1D6FB}V_{m})\cdot \boldsymbol{n}=0\end{array}\biggr\} & \displaystyle \text{for PE (7.6)},\\ \displaystyle (\boldsymbol{\unicode[STIX]{x1D6F4}}\unicode[STIX]{x1D6FB}V_{m})\cdot \boldsymbol{n}=0 & \displaystyle \text{for monodomain (7.11)},\\ \displaystyle (\boldsymbol{M}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D713})\cdot \boldsymbol{n}=0 & \displaystyle \text{for eikonal-diffusion (7.14)}.\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
Moreover, for the bidomain problems (7.5) and (7.6), they force the following compatibility conditions on the applied external currents:
 $$\begin{eqnarray}\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}I_{i}^{\mathit{ext}}=\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}I_{e}^{\mathit{ext}}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}I_{i}^{\mathit{ext}}=\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}I_{e}^{\mathit{ext}}.\end{eqnarray}$$
On the internal surface
![]() $\unicode[STIX]{x1D6F4}_{\mathit{endo}}$
of the endocardium, again Neumann conditions are prescribed. In this case, however, they could be non-homogeneous at specific stimulation points (e.g. the atrioventricular node and the points of the bundle of His). For the eikonal problem, Dirichlet data on the activation time could be prescribed at some specific locations if they are available, thanks to the NavX system, for example; see Section 6.2 (Sermesant et al.
Reference Sermesant, Chabiniok, Chinchapatnam, Mansi, Billet, Moireau, Peyrat, Wong, Relan, Rhode, Ginks, Lambiase, Delingette, Sorine, Rinaldi, Chapelle, Razavi and Ayache2012). When redundant (e.g. when the electrical problem in the myocardium is coupled with the Purkinje network: see below) these data have been used to solve inverse problems, for example to estimate the conduction velocity in the myocardium (Sermesant et al.
Reference Sermesant, Chabiniok, Chinchapatnam, Mansi, Billet, Moireau, Peyrat, Wong, Relan, Rhode, Ginks, Lambiase, Delingette, Sorine, Rinaldi, Chapelle, Razavi and Ayache2012) or to obtain personalized Purkinje networks (Vergara et al.
Reference Vergara, Palamara, Catanzariti, Nobile, Faggiano, Pangrazzi, Centonze, Maines, Quarteroni and Vergara2014, Palamara et al.
Reference Palamara, Vergara, Catanzariti, Faggiano, Centonze, Pangrazzi, Maines and Quarteroni2014, Reference Palamara, Vergara, Faggiano and Nobile2015).
$\unicode[STIX]{x1D6F4}_{\mathit{endo}}$
of the endocardium, again Neumann conditions are prescribed. In this case, however, they could be non-homogeneous at specific stimulation points (e.g. the atrioventricular node and the points of the bundle of His). For the eikonal problem, Dirichlet data on the activation time could be prescribed at some specific locations if they are available, thanks to the NavX system, for example; see Section 6.2 (Sermesant et al.
Reference Sermesant, Chabiniok, Chinchapatnam, Mansi, Billet, Moireau, Peyrat, Wong, Relan, Rhode, Ginks, Lambiase, Delingette, Sorine, Rinaldi, Chapelle, Razavi and Ayache2012). When redundant (e.g. when the electrical problem in the myocardium is coupled with the Purkinje network: see below) these data have been used to solve inverse problems, for example to estimate the conduction velocity in the myocardium (Sermesant et al.
Reference Sermesant, Chabiniok, Chinchapatnam, Mansi, Billet, Moireau, Peyrat, Wong, Relan, Rhode, Ginks, Lambiase, Delingette, Sorine, Rinaldi, Chapelle, Razavi and Ayache2012) or to obtain personalized Purkinje networks (Vergara et al.
Reference Vergara, Palamara, Catanzariti, Nobile, Faggiano, Pangrazzi, Centonze, Maines, Quarteroni and Vergara2014, Palamara et al.
Reference Palamara, Vergara, Catanzariti, Faggiano, Centonze, Pangrazzi, Maines and Quarteroni2014, Reference Palamara, Vergara, Faggiano and Nobile2015).
If the mathematical model accounts for the presence of the Purkinje network, interface conditions on
![]() $\unicode[STIX]{x1D6F4}_{\mathit{endo}}$
describing the continuity of the current and of the potential at the Purkinje muscle junctions (PMJs) are implicitly provided for the bidomain and monodomain problems by the solution of the coupled muscle region/Purkinje network problem (Vigmond and Clements Reference Vigmond and Clements2007, Vergara et al.
Reference Vergara, Lange, Palamara, Lassila, Frangi and Quarteroni2016). For the sake of exposition, we will not detail the bidomain and monodomain models for the Purkinje network, instead referring interested readers to Vigmond and Clements (Reference Vigmond and Clements2007), Bordas et al. (Reference Bordas, Gillow, Gavaghan, Rodríguez and Kay2012) and Vergara et al. (Reference Vergara, Lange, Palamara, Lassila, Frangi and Quarteroni2016). We will only note that, unlike the muscular case, in the network the gap junctions connecting two consecutive Purkinje cells are often explicitly modelled by means of resistances. Specific Purkinje cell models have also been developed, with the same structure as those developed for the muscular cells: see e.g. DiFrancesco and Noble (Reference Difrancesco and Noble1985). However, we will describe the mechanisms of coupling; in particular, we will refer to the coupled problem obtained by considering the monodomain problem both in the muscle region and in the Purkinje network (Vergara et al.
Reference Vergara, Lange, Palamara, Lassila, Frangi and Quarteroni2016). We consider
$\unicode[STIX]{x1D6F4}_{\mathit{endo}}$
describing the continuity of the current and of the potential at the Purkinje muscle junctions (PMJs) are implicitly provided for the bidomain and monodomain problems by the solution of the coupled muscle region/Purkinje network problem (Vigmond and Clements Reference Vigmond and Clements2007, Vergara et al.
Reference Vergara, Lange, Palamara, Lassila, Frangi and Quarteroni2016). For the sake of exposition, we will not detail the bidomain and monodomain models for the Purkinje network, instead referring interested readers to Vigmond and Clements (Reference Vigmond and Clements2007), Bordas et al. (Reference Bordas, Gillow, Gavaghan, Rodríguez and Kay2012) and Vergara et al. (Reference Vergara, Lange, Palamara, Lassila, Frangi and Quarteroni2016). We will only note that, unlike the muscular case, in the network the gap junctions connecting two consecutive Purkinje cells are often explicitly modelled by means of resistances. Specific Purkinje cell models have also been developed, with the same structure as those developed for the muscular cells: see e.g. DiFrancesco and Noble (Reference Difrancesco and Noble1985). However, we will describe the mechanisms of coupling; in particular, we will refer to the coupled problem obtained by considering the monodomain problem both in the muscle region and in the Purkinje network (Vergara et al.
Reference Vergara, Lange, Palamara, Lassila, Frangi and Quarteroni2016). We consider
![]() $N$
Purkinje muscle junctions located at
$N$
Purkinje muscle junctions located at
![]() $\boldsymbol{x}=\boldsymbol{s}_{j}$
and we assume that each of them could be modelled by means of a resistance
$\boldsymbol{x}=\boldsymbol{s}_{j}$
and we assume that each of them could be modelled by means of a resistance
![]() $R_{\mathit{PMJ}}$
. Then, the monodomain/monodomain coupled problem reads as follows. For each
$R_{\mathit{PMJ}}$
. Then, the monodomain/monodomain coupled problem reads as follows. For each
![]() $t>0$
, find
$t>0$
, find
 $V_{p},\,V_{m},\,\boldsymbol{w}_{p},\,\boldsymbol{w}$
and
$V_{p},\,V_{m},\,\boldsymbol{w}_{p},\,\boldsymbol{w}$
and
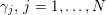 $\unicode[STIX]{x1D6FE}_{j},\,j=1,\ldots ,N$
, such that
$\unicode[STIX]{x1D6FE}_{j},\,j=1,\ldots ,N$
, such that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle P_{m}\biggl(V_{m},\boldsymbol{w},\mathop{\sum }_{j=1}^{N}\frac{1}{A_{r}}{\mathcal{I}}_{{\mathcal{B}}_{r}(\boldsymbol{s}_{j})}\unicode[STIX]{x1D6FE}_{j}+I^{\mathit{ext}}\biggr)=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle P_{m}\biggl(V_{m},\boldsymbol{w},\mathop{\sum }_{j=1}^{N}\frac{1}{A_{r}}{\mathcal{I}}_{{\mathcal{B}}_{r}(\boldsymbol{s}_{j})}\unicode[STIX]{x1D6FE}_{j}+I^{\mathit{ext}}\biggr)=0,\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle P_{p}(V_{p},\boldsymbol{w}_{p},\boldsymbol{\unicode[STIX]{x1D6FE}})=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle P_{p}(V_{p},\boldsymbol{w}_{p},\boldsymbol{\unicode[STIX]{x1D6FE}})=0,\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D6FE}_{j}=\frac{V_{p}(\boldsymbol{s}_{j})-{\textstyle \frac{1}{A_{r}}}\int _{{\mathcal{B}}_{r}(\boldsymbol{s}_{j})}V_{m}\text{d}\boldsymbol{x}}{R_{\mathit{PMJ}}}\quad j=1,\ldots ,N,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D6FE}_{j}=\frac{V_{p}(\boldsymbol{s}_{j})-{\textstyle \frac{1}{A_{r}}}\int _{{\mathcal{B}}_{r}(\boldsymbol{s}_{j})}V_{m}\text{d}\boldsymbol{x}}{R_{\mathit{PMJ}}}\quad j=1,\ldots ,N,\end{eqnarray}$$
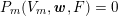 $P_{m}(V_{m},\boldsymbol{w},F)=0$
denotes the monodomain problem in the myocardium with source term
$P_{m}(V_{m},\boldsymbol{w},F)=0$
denotes the monodomain problem in the myocardium with source term
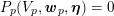 $P_{p}(V_{p},\boldsymbol{w}_{p},\boldsymbol{\unicode[STIX]{x1D702}})=0$
is the monodomain problem in the Purkinje network with Neumann conditions with data
$P_{p}(V_{p},\boldsymbol{w}_{p},\boldsymbol{\unicode[STIX]{x1D702}})=0$
is the monodomain problem in the Purkinje network with Neumann conditions with data
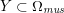 $Y\subset \unicode[STIX]{x1D6FA}_{\mathit{mus}}$
,
$Y\subset \unicode[STIX]{x1D6FA}_{\mathit{mus}}$
,
The coupling between eikonal muscular and Purkinje network problems has been addressed by Vergara et al. (Reference Vergara, Palamara, Catanzariti, Nobile, Faggiano, Pangrazzi, Centonze, Maines, Quarteroni and Vergara2014) for normal propagation and Palamara et al. (Reference Palamara, Vergara, Catanzariti, Faggiano, Centonze, Pangrazzi, Maines and Quarteroni2014) for pathological propagations.
7.1.5 Computing the surface electrocardiogram signals
The computation of the potentials related to electrical propagation in the heart could be used to numerically compute the surface electrocardiogram (ECG) signals, that is, electrical potential on the surface of the body, thus simulating what happens in normal clinical practice. This could be obtained by coupling the bidomain or monodomain problem with the propagation in the torso, modelled by a simple diffusion problem for the extracellular potential at each
![]() $t>0$
:
$t>0$
:
 $$\begin{eqnarray}\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{\unicode[STIX]{x1D6F4}}_{T}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D719}_{T})=0\quad \text{in }\unicode[STIX]{x1D6FA}_{T},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{\unicode[STIX]{x1D6F4}}_{T}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D719}_{T})=0\quad \text{in }\unicode[STIX]{x1D6FA}_{T},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FA}_{T}$
is the torso domain that surrounds the heart domain
$\unicode[STIX]{x1D6FA}_{T}$
is the torso domain that surrounds the heart domain
![]() $\unicode[STIX]{x1D6FA}_{\mathit{mus}}$
(i.e. the heart boundary surface
$\unicode[STIX]{x1D6FA}_{\mathit{mus}}$
(i.e. the heart boundary surface
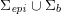 $\unicode[STIX]{x1D6F4}_{\mathit{epi}}\cup \unicode[STIX]{x1D6F4}_{b}$
denotes the interface with the torso),
$\unicode[STIX]{x1D6F4}_{\mathit{epi}}\cup \unicode[STIX]{x1D6F4}_{b}$
denotes the interface with the torso),
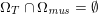 $\unicode[STIX]{x1D6FA}_{T}\cap \unicode[STIX]{x1D6FA}_{\mathit{mus}}=\emptyset$
, with
$\unicode[STIX]{x1D6FA}_{T}\cap \unicode[STIX]{x1D6FA}_{\mathit{mus}}=\emptyset$
, with
![]() $\unicode[STIX]{x1D719}_{T}$
denoting the extracellular potential in the torso. Homogeneous Neumann conditions have to be applied on the external torso surface
$\unicode[STIX]{x1D719}_{T}$
denoting the extracellular potential in the torso. Homogeneous Neumann conditions have to be applied on the external torso surface
![]() $\unicode[STIX]{x1D6F4}_{T}$
, whereas the following interface conditions, which replace the boundary conditions for the heart problem, need to be prescribed at the torso/heart interface:
$\unicode[STIX]{x1D6F4}_{T}$
, whereas the following interface conditions, which replace the boundary conditions for the heart problem, need to be prescribed at the torso/heart interface:
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}ll@{}}\displaystyle \unicode[STIX]{x1D719}_{e}=\unicode[STIX]{x1D719}_{T} & \displaystyle \text{on }\unicode[STIX]{x1D6F4}_{\mathit{epi}}\cup \unicode[STIX]{x1D6F4}_{b},\\ \displaystyle (\boldsymbol{\unicode[STIX]{x1D6F4}}_{e}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D719}_{e})\cdot \boldsymbol{n}=(\boldsymbol{\unicode[STIX]{x1D6F4}}_{T}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D719}_{T})\cdot \boldsymbol{n} & \displaystyle \text{on }\unicode[STIX]{x1D6F4}_{\mathit{epi}}\cup \unicode[STIX]{x1D6F4}_{b},\\ \displaystyle (\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}\unicode[STIX]{x1D6FB}(V_{m}+\unicode[STIX]{x1D719}_{e}))\cdot \boldsymbol{n}=0 & \displaystyle \text{on }\unicode[STIX]{x1D6F4}_{\mathit{epi}}\cup \unicode[STIX]{x1D6F4}_{b}.\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}ll@{}}\displaystyle \unicode[STIX]{x1D719}_{e}=\unicode[STIX]{x1D719}_{T} & \displaystyle \text{on }\unicode[STIX]{x1D6F4}_{\mathit{epi}}\cup \unicode[STIX]{x1D6F4}_{b},\\ \displaystyle (\boldsymbol{\unicode[STIX]{x1D6F4}}_{e}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D719}_{e})\cdot \boldsymbol{n}=(\boldsymbol{\unicode[STIX]{x1D6F4}}_{T}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D719}_{T})\cdot \boldsymbol{n} & \displaystyle \text{on }\unicode[STIX]{x1D6F4}_{\mathit{epi}}\cup \unicode[STIX]{x1D6F4}_{b},\\ \displaystyle (\boldsymbol{\unicode[STIX]{x1D6F4}}_{i}\unicode[STIX]{x1D6FB}(V_{m}+\unicode[STIX]{x1D719}_{e}))\cdot \boldsymbol{n}=0 & \displaystyle \text{on }\unicode[STIX]{x1D6F4}_{\mathit{epi}}\cup \unicode[STIX]{x1D6F4}_{b}.\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
7.1.6 Numerical discretization
Numerical solution of the bidomain and monodomain problems is very demanding. Together with the strict constraint on the spatial mesh size due to the propagation of a very steep front (see Section 6.1), a time step of the order of tenths or even hundredths of milliseconds must be used in order to capture the fast dynamics characterizing the propagation, with time constants of the order of
![]() $0.1$
ms. Moreover, as discussed below, the algebraic solution of the linear systems arising at each time step using finite elements, for example, requires careful treatment, due to the coupled nature of the problem, the singularity of some of the matrices involved, and the presence of the non-linear term due to the ionic currents.
$0.1$
ms. Moreover, as discussed below, the algebraic solution of the linear systems arising at each time step using finite elements, for example, requires careful treatment, due to the coupled nature of the problem, the singularity of some of the matrices involved, and the presence of the non-linear term due to the ionic currents.
Several time discretization strategies have been considered so far. We can group them into four main categories, explicit, semi-implicit, implicit and operator splitting-based methods, which are now presented briefly. We start by introducing the finite element matrices and vectors:
 $$\begin{eqnarray}\displaystyle (M)_{jk} & = & \displaystyle \int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\unicode[STIX]{x1D713}_{k}\unicode[STIX]{x1D713}_{j}\text{d}\unicode[STIX]{x1D714},\nonumber\\ \displaystyle (A_{\unicode[STIX]{x1D6FD}})_{jk} & = & \displaystyle \int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\boldsymbol{\unicode[STIX]{x1D6F4}}_{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D713}_{k}\cdot \unicode[STIX]{x1D6FB}\unicode[STIX]{x1D713}_{j}\text{d}\unicode[STIX]{x1D714},\quad \unicode[STIX]{x1D6FD}=i,e\nonumber\\ \displaystyle (\boldsymbol{I}_{\mathit{ion}}(\boldsymbol{V}_{m}^{n},\boldsymbol{W}^{r},\boldsymbol{C}^{s}))_{j} & = & \displaystyle \int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}I_{\mathit{ion}}(V_{m}^{n},\boldsymbol{w}^{r},\boldsymbol{c}^{s})\unicode[STIX]{x1D713}_{j}\text{d}\unicode[STIX]{x1D714},\nonumber\\ \displaystyle (\boldsymbol{G}(\boldsymbol{V}_{m}^{n},\boldsymbol{W}^{r}))_{j} & = & \displaystyle \int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\boldsymbol{g}(V_{m}^{n},\boldsymbol{w}^{r})\cdot \boldsymbol{y}_{j}\text{d}\unicode[STIX]{x1D714},\nonumber\\ \displaystyle (\boldsymbol{S}(\boldsymbol{V}_{m}^{n},\boldsymbol{W}^{r},\boldsymbol{C}^{s}))_{j} & = & \displaystyle \int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\boldsymbol{g}_{c}(V_{m}^{n},\boldsymbol{w}^{r},\boldsymbol{c}^{s})\cdot \boldsymbol{\unicode[STIX]{x1D701}}_{j}\text{d}\unicode[STIX]{x1D714},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (M)_{jk} & = & \displaystyle \int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\unicode[STIX]{x1D713}_{k}\unicode[STIX]{x1D713}_{j}\text{d}\unicode[STIX]{x1D714},\nonumber\\ \displaystyle (A_{\unicode[STIX]{x1D6FD}})_{jk} & = & \displaystyle \int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\boldsymbol{\unicode[STIX]{x1D6F4}}_{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D713}_{k}\cdot \unicode[STIX]{x1D6FB}\unicode[STIX]{x1D713}_{j}\text{d}\unicode[STIX]{x1D714},\quad \unicode[STIX]{x1D6FD}=i,e\nonumber\\ \displaystyle (\boldsymbol{I}_{\mathit{ion}}(\boldsymbol{V}_{m}^{n},\boldsymbol{W}^{r},\boldsymbol{C}^{s}))_{j} & = & \displaystyle \int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}I_{\mathit{ion}}(V_{m}^{n},\boldsymbol{w}^{r},\boldsymbol{c}^{s})\unicode[STIX]{x1D713}_{j}\text{d}\unicode[STIX]{x1D714},\nonumber\\ \displaystyle (\boldsymbol{G}(\boldsymbol{V}_{m}^{n},\boldsymbol{W}^{r}))_{j} & = & \displaystyle \int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\boldsymbol{g}(V_{m}^{n},\boldsymbol{w}^{r})\cdot \boldsymbol{y}_{j}\text{d}\unicode[STIX]{x1D714},\nonumber\\ \displaystyle (\boldsymbol{S}(\boldsymbol{V}_{m}^{n},\boldsymbol{W}^{r},\boldsymbol{C}^{s}))_{j} & = & \displaystyle \int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\boldsymbol{g}_{c}(V_{m}^{n},\boldsymbol{w}^{r},\boldsymbol{c}^{s})\cdot \boldsymbol{\unicode[STIX]{x1D701}}_{j}\text{d}\unicode[STIX]{x1D714},\nonumber\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D713}_{i},\,\boldsymbol{y}_{j}$
and
$\unicode[STIX]{x1D713}_{i},\,\boldsymbol{y}_{j}$
and
![]() $\boldsymbol{\unicode[STIX]{x1D701}}_{j}$
denote the basis functions of the finite element spaces, and
$\boldsymbol{\unicode[STIX]{x1D701}}_{j}$
denote the basis functions of the finite element spaces, and
![]() $n,r,s$
are integers denoting discretized times. Vectors
$n,r,s$
are integers denoting discretized times. Vectors
![]() $\boldsymbol{V}_{m}$
,
$\boldsymbol{V}_{m}$
,
![]() $\boldsymbol{\unicode[STIX]{x1D6F7}}_{e}$
,
$\boldsymbol{\unicode[STIX]{x1D6F7}}_{e}$
,
![]() $\boldsymbol{\unicode[STIX]{x1D6F7}}_{i}$
,
$\boldsymbol{\unicode[STIX]{x1D6F7}}_{i}$
,
![]() $\boldsymbol{W}$
and
$\boldsymbol{W}$
and
![]() $\boldsymbol{C}$
denote the unknown coefficients of the finite element solutions associated with the unknowns
$\boldsymbol{C}$
denote the unknown coefficients of the finite element solutions associated with the unknowns
![]() $V_{m}$
,
$V_{m}$
,
![]() $\unicode[STIX]{x1D719}_{e}$
,
$\unicode[STIX]{x1D719}_{e}$
,
![]() $\unicode[STIX]{x1D719}_{i}$
,
$\unicode[STIX]{x1D719}_{i}$
,
![]() $\boldsymbol{w}$
,
$\boldsymbol{w}$
,
![]() $\boldsymbol{c}$
. Note that the dimensions of
$\boldsymbol{c}$
. Note that the dimensions of
![]() $\boldsymbol{W}$
and
$\boldsymbol{W}$
and
![]() $\boldsymbol{C}$
are
$\boldsymbol{C}$
are
![]() $MK$
and
$MK$
and
![]() $SK$
, respectively, where
$SK$
, respectively, where
![]() $K$
is the number of degrees of freedom associated with the mesh and the choice of finite elements (e.g. the number of vertices for linear finite elements). In all the cases, in order to simplify the notation, we will set
$K$
is the number of degrees of freedom associated with the mesh and the choice of finite elements (e.g. the number of vertices for linear finite elements). In all the cases, in order to simplify the notation, we will set
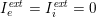 $I_{e}^{\mathit{ext}}=I_{i}^{\mathit{ext}}=0$
, and we assume that the running temporal index
$I_{e}^{\mathit{ext}}=I_{i}^{\mathit{ext}}=0$
, and we assume that the running temporal index
![]() $^{n+1}$
is understood.
$^{n+1}$
is understood.
Explicit methods.
In explicit methods, all the problems in (7.10) are discretized by means of an explicit scheme, for example forward Euler for both the PDE and ODE systems (Puwal and Roth Reference Puwal and Roth2007, Ethier and Bourgault Reference Ethier and Bourgault2008). This choice allows us to decouple the four blocks of the bidomain system (the two PDEs and the two ODEs system), involving only the mass matrix in the PP formulation, and thus in principle avoiding the need to solve any linear system provided that mass lumping is performed. In contrast, for the PE formulation, the absence of time derivatives in the second PDE implies that a linear system in the unknown
![]() $\boldsymbol{\unicode[STIX]{x1D6F7}}_{e}$
needs to be solved in any case (we detail the forward Euler method):
$\boldsymbol{\unicode[STIX]{x1D6F7}}_{e}$
needs to be solved in any case (we detail the forward Euler method):
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D712}_{m}C_{m}M\frac{\boldsymbol{V}_{m}-\boldsymbol{V}_{m}^{n}}{\unicode[STIX]{x1D6E5}t}=-A_{i}(\boldsymbol{V}_{m}^{n}+\boldsymbol{\unicode[STIX]{x1D6F7}}_{e}^{n})-\unicode[STIX]{x1D712}_{m}\boldsymbol{I}_{\mathit{ion}}(\boldsymbol{V}_{m}^{n},\boldsymbol{W}^{n},\boldsymbol{C}^{n}),\nonumber\\ \displaystyle & & \displaystyle \displaystyle A_{i}\boldsymbol{V}_{m}+(A_{i}+A_{e})\boldsymbol{\unicode[STIX]{x1D6F7}}_{e}=\mathbf{0},\nonumber\\ \displaystyle & & \displaystyle \displaystyle M\frac{\boldsymbol{W}-\boldsymbol{W}^{n}}{\unicode[STIX]{x1D6E5}t}=\boldsymbol{G}(\boldsymbol{V}_{m}^{n},\boldsymbol{W}^{n}),\quad M\frac{\boldsymbol{C}-\boldsymbol{C}^{n}}{\unicode[STIX]{x1D6E5}t}=\boldsymbol{S}(\boldsymbol{V}_{m}^{n},\boldsymbol{W}^{n},\boldsymbol{C}^{n}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D712}_{m}C_{m}M\frac{\boldsymbol{V}_{m}-\boldsymbol{V}_{m}^{n}}{\unicode[STIX]{x1D6E5}t}=-A_{i}(\boldsymbol{V}_{m}^{n}+\boldsymbol{\unicode[STIX]{x1D6F7}}_{e}^{n})-\unicode[STIX]{x1D712}_{m}\boldsymbol{I}_{\mathit{ion}}(\boldsymbol{V}_{m}^{n},\boldsymbol{W}^{n},\boldsymbol{C}^{n}),\nonumber\\ \displaystyle & & \displaystyle \displaystyle A_{i}\boldsymbol{V}_{m}+(A_{i}+A_{e})\boldsymbol{\unicode[STIX]{x1D6F7}}_{e}=\mathbf{0},\nonumber\\ \displaystyle & & \displaystyle \displaystyle M\frac{\boldsymbol{W}-\boldsymbol{W}^{n}}{\unicode[STIX]{x1D6E5}t}=\boldsymbol{G}(\boldsymbol{V}_{m}^{n},\boldsymbol{W}^{n}),\quad M\frac{\boldsymbol{C}-\boldsymbol{C}^{n}}{\unicode[STIX]{x1D6E5}t}=\boldsymbol{S}(\boldsymbol{V}_{m}^{n},\boldsymbol{W}^{n},\boldsymbol{C}^{n}).\nonumber\end{eqnarray}$$
Explicit methods lead to a severe constraint on the time discretization of the type
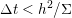 $\unicode[STIX]{x1D6E5}t<h^{2}/\unicode[STIX]{x1D6F4}$
, where
$\unicode[STIX]{x1D6E5}t<h^{2}/\unicode[STIX]{x1D6F4}$
, where
![]() $\unicode[STIX]{x1D6F4}$
is a representative value of the conductivity (Puwal and Roth Reference Puwal and Roth2007). Dos Santos, Plank, Bauer and Vigmond Reference dos Santos, Plank, Bauer, Vigmond and Kornhuber2005 showed for a model problem that an explicit method is not absolutely stable for a value of
$\unicode[STIX]{x1D6F4}$
is a representative value of the conductivity (Puwal and Roth Reference Puwal and Roth2007). Dos Santos, Plank, Bauer and Vigmond Reference dos Santos, Plank, Bauer, Vigmond and Kornhuber2005 showed for a model problem that an explicit method is not absolutely stable for a value of
![]() $\unicode[STIX]{x1D6E5}t$
much smaller than that required to capture the front propagation. For this reason and due to the increased CPU availability, explicit methods are no longer used so often.
$\unicode[STIX]{x1D6E5}t$
much smaller than that required to capture the front propagation. For this reason and due to the increased CPU availability, explicit methods are no longer used so often.
Semi-implicit methods.
ODE systems are usually solved at each time step by means of explicit or semi-implicit methods (in the latter case the dependence on
![]() $V_{m}$
is treated explicitly). This suggests using semi-implicit methods (Keener and Bogar Reference Keener and Bogar1998, Pennacchio and Simoncini Reference Pennacchio and Simoncini2002, Colli Franzone and Pavarino Reference Colli Franzone and Pavarino2004) for the whole coupled PDE/ODE problem. These methods are the most widely used together with operator splitting-based methods (see below). They are based on treating the diffusive term implicitly and the non-linear term explicitly. A possible semi-implicit (first-order) scheme for the PP formulation (7.10) is as follows:
$V_{m}$
is treated explicitly). This suggests using semi-implicit methods (Keener and Bogar Reference Keener and Bogar1998, Pennacchio and Simoncini Reference Pennacchio and Simoncini2002, Colli Franzone and Pavarino Reference Colli Franzone and Pavarino2004) for the whole coupled PDE/ODE problem. These methods are the most widely used together with operator splitting-based methods (see below). They are based on treating the diffusive term implicitly and the non-linear term explicitly. A possible semi-implicit (first-order) scheme for the PP formulation (7.10) is as follows:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle M\frac{\boldsymbol{W}-\boldsymbol{W}^{n}}{\unicode[STIX]{x1D6E5}t}-\boldsymbol{G}(\boldsymbol{V}_{m}^{n},\boldsymbol{W})=\mathbf{0},\quad M\frac{\boldsymbol{C}-\boldsymbol{C}^{n}}{\unicode[STIX]{x1D6E5}t}-\boldsymbol{S}(\boldsymbol{V}_{m}^{n},\boldsymbol{W},\boldsymbol{C})=\mathbf{0},\nonumber\\ \displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D712}_{m}C_{m}M\frac{\boldsymbol{V}_{m}-\boldsymbol{V}_{m}^{n}}{\unicode[STIX]{x1D6E5}t}+A_{i}\boldsymbol{\unicode[STIX]{x1D6F7}}_{i}+\unicode[STIX]{x1D712}_{m}\boldsymbol{I}_{\mathit{ion}}(\boldsymbol{V}_{m}^{n},\boldsymbol{W},\boldsymbol{C})=\mathbf{0},\nonumber\\ \displaystyle & & \displaystyle \displaystyle -\unicode[STIX]{x1D712}_{m}C_{m}M\frac{\boldsymbol{V}_{m}-\boldsymbol{V}_{m}^{n}}{\unicode[STIX]{x1D6E5}t}+A_{e}\boldsymbol{\unicode[STIX]{x1D6F7}}_{e}-\unicode[STIX]{x1D712}_{m}\boldsymbol{I}_{\mathit{ion}}(\boldsymbol{V}_{m}^{n},\boldsymbol{W},\boldsymbol{C})=\mathbf{0}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle M\frac{\boldsymbol{W}-\boldsymbol{W}^{n}}{\unicode[STIX]{x1D6E5}t}-\boldsymbol{G}(\boldsymbol{V}_{m}^{n},\boldsymbol{W})=\mathbf{0},\quad M\frac{\boldsymbol{C}-\boldsymbol{C}^{n}}{\unicode[STIX]{x1D6E5}t}-\boldsymbol{S}(\boldsymbol{V}_{m}^{n},\boldsymbol{W},\boldsymbol{C})=\mathbf{0},\nonumber\\ \displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D712}_{m}C_{m}M\frac{\boldsymbol{V}_{m}-\boldsymbol{V}_{m}^{n}}{\unicode[STIX]{x1D6E5}t}+A_{i}\boldsymbol{\unicode[STIX]{x1D6F7}}_{i}+\unicode[STIX]{x1D712}_{m}\boldsymbol{I}_{\mathit{ion}}(\boldsymbol{V}_{m}^{n},\boldsymbol{W},\boldsymbol{C})=\mathbf{0},\nonumber\\ \displaystyle & & \displaystyle \displaystyle -\unicode[STIX]{x1D712}_{m}C_{m}M\frac{\boldsymbol{V}_{m}-\boldsymbol{V}_{m}^{n}}{\unicode[STIX]{x1D6E5}t}+A_{e}\boldsymbol{\unicode[STIX]{x1D6F7}}_{e}-\unicode[STIX]{x1D712}_{m}\boldsymbol{I}_{\mathit{ion}}(\boldsymbol{V}_{m}^{n},\boldsymbol{W},\boldsymbol{C})=\mathbf{0}\nonumber\end{eqnarray}$$
(see e.g. Colli Franzone and Pavarino Reference Colli Franzone and Pavarino2004).
A semi-implicit method like the one reported here has two nice properties. First of all, the two PDEs are decoupled by the ODE systems, greatly simplifying the numerical solution of the entire problem. This decoupling strategy is justified by noticing that the Jacobian matrices of a fully implicit discretization feature dominant values on the diagonal, suggesting weak coupling between potentials and gating/ionic concentration variables (Munteanu, Pavarino and Scacchi Reference Munteanu, Pavarino and Scacchi2009). Secondly, it allows for a linearization of the non-linear reaction term given by the ionic currents, thus requiring the solution of a
![]() $2\times 2$
block linear system.
$2\times 2$
block linear system.
Special attention has been paid to evaluation of the ionic current in a finite element context. In particular, two strategies have mainly been considered, namely ionic current interpolation (ICI) and state variable interpolation (SVI). In the first case, only the nodal values are used to build an interpolation of the ionic current, whereas in the second case the trans-membrane potential and the gating/ionic concentration variables are interpolated within each element and the ionic current is then evaluated by using these interpolated variables (Pathmanathan et al. Reference Pathmanathan, Mirams, Southern and Whiteley2011). The ICI approach is of course more efficient from the computational point of view, and allows expression of the reaction term by means of a mass matrix. However, it has lower accuracy with respect to state variable interpolation; in particular, the computed conduction velocity is generally larger than the true velocity: see Pathmanathan et al. (Reference Pathmanathan, Mirams, Southern and Whiteley2011).
From the algebraic point of view, the solution of a semi-implicit discretized problem is very demanding, since the matrix of the linear system associated with the PDEs written in terms of the unknowns
![]() $\boldsymbol{\unicode[STIX]{x1D6F7}}_{i}$
and
$\boldsymbol{\unicode[STIX]{x1D6F7}}_{i}$
and
![]() $\boldsymbol{\unicode[STIX]{x1D6F7}}_{e}$
is given by
$\boldsymbol{\unicode[STIX]{x1D6F7}}_{e}$
is given by
 $$\begin{eqnarray}B=\frac{\unicode[STIX]{x1D712}_{m}C_{m}}{\unicode[STIX]{x1D6E5}t}\left[\begin{array}{@{}cc@{}}M & -M\\ -M & M\end{array}\right]+\left[\begin{array}{@{}cc@{}}A_{i} & 0\\ 0 & A_{e}\end{array}\right]\!.\end{eqnarray}$$
$$\begin{eqnarray}B=\frac{\unicode[STIX]{x1D712}_{m}C_{m}}{\unicode[STIX]{x1D6E5}t}\left[\begin{array}{@{}cc@{}}M & -M\\ -M & M\end{array}\right]+\left[\begin{array}{@{}cc@{}}A_{i} & 0\\ 0 & A_{e}\end{array}\right]\!.\end{eqnarray}$$
Both terms of this matrix are singular, the first due to the degenerate parabolic nature of the PP bidomain formulation and the second since each block
![]() $A_{\unicode[STIX]{x1D6FD}}$
is related to a pure Neumann diffusive problem. However, matrix
$A_{\unicode[STIX]{x1D6FD}}$
is related to a pure Neumann diffusive problem. However, matrix
![]() $B$
is positive semidefinite, so the preconditioned conjugate gradient method is often used for its numerical solution (Pennacchio and Simoncini Reference Pennacchio and Simoncini2002, Colli Franzone and Pavarino Reference Colli Franzone and Pavarino2004). Preconditioning is needed since the matrix
$B$
is positive semidefinite, so the preconditioned conjugate gradient method is often used for its numerical solution (Pennacchio and Simoncini Reference Pennacchio and Simoncini2002, Colli Franzone and Pavarino Reference Colli Franzone and Pavarino2004). Preconditioning is needed since the matrix
![]() $B$
is highly ill-conditioned, due to the block
$B$
is highly ill-conditioned, due to the block
![]() $2\times 2$
mass matrix which, unlike the classical mass matrix, worsens the spectrum of the stiffness matrix. Efficient preconditioners include block Jacobi and Gauss–Seidel (Mardal et al.
Reference Mardal, Nielsen, Cai and Tveito2007), block SSOR (Pennacchio and Simoncini Reference Pennacchio and Simoncini2002), multilevel additive Schwarz (Pavarino and Scacchi Reference Pavarino and Scacchi2008), multigrid (Plank et al.
Reference Plank, Liebmann, dos Santos, Vigmond and Haase2007, Vigmond et al.
Reference Vigmond, dos Santos, Prassl, Deo and Plank2008), and a functional block preconditioner obtained by the monodomain solver (Gerardo-Giorda et al.
Reference Gerardo-Giorda, Mirabella, Nobile, Perego and Veneziani2009).
$2\times 2$
mass matrix which, unlike the classical mass matrix, worsens the spectrum of the stiffness matrix. Efficient preconditioners include block Jacobi and Gauss–Seidel (Mardal et al.
Reference Mardal, Nielsen, Cai and Tveito2007), block SSOR (Pennacchio and Simoncini Reference Pennacchio and Simoncini2002), multilevel additive Schwarz (Pavarino and Scacchi Reference Pavarino and Scacchi2008), multigrid (Plank et al.
Reference Plank, Liebmann, dos Santos, Vigmond and Haase2007, Vigmond et al.
Reference Vigmond, dos Santos, Prassl, Deo and Plank2008), and a functional block preconditioner obtained by the monodomain solver (Gerardo-Giorda et al.
Reference Gerardo-Giorda, Mirabella, Nobile, Perego and Veneziani2009).
Semi-implicit methods have also been proposed for the PE formulation: see e.g. Fernández and Zemzemi (Reference Fernández and Zemzemi2010). For example, with respect to the unknowns
![]() $\boldsymbol{V}_{m}$
and
$\boldsymbol{V}_{m}$
and
![]() $\boldsymbol{\unicode[STIX]{x1D6F7}}_{e}$
, we have
$\boldsymbol{\unicode[STIX]{x1D6F7}}_{e}$
, we have
 $$\begin{eqnarray}B=\frac{\unicode[STIX]{x1D712}_{m}C_{m}}{\unicode[STIX]{x1D6E5}t}\left[\begin{array}{@{}cc@{}}M & 0\\ 0 & 0\end{array}\right]+\left[\begin{array}{@{}cc@{}}A_{i} & A_{i}\\ A_{i} & A_{i}+A_{e}\end{array}\right]\!.\end{eqnarray}$$
$$\begin{eqnarray}B=\frac{\unicode[STIX]{x1D712}_{m}C_{m}}{\unicode[STIX]{x1D6E5}t}\left[\begin{array}{@{}cc@{}}M & 0\\ 0 & 0\end{array}\right]+\left[\begin{array}{@{}cc@{}}A_{i} & A_{i}\\ A_{i} & A_{i}+A_{e}\end{array}\right]\!.\end{eqnarray}$$
Again the matrix is singular, ill-conditioned, and semidefinite positive. In this context, we cite Pierre (Reference Pierre2012) for an incomplete block LU factorization preconditioner, and Vigmond, Aguel and Trayanova (Reference Vigmond, Aguel and Trayanova2002), where the two PDEs are decoupled by treating
![]() $V_{m}$
explicitly in (7.6a
) and
$V_{m}$
explicitly in (7.6a
) and
![]() $\unicode[STIX]{x1D719}_{e}$
in (7.6b
).
$\unicode[STIX]{x1D719}_{e}$
in (7.6b
).
In any case, semi-implicit methods are conditionally stable with a bound on
![]() $\unicode[STIX]{x1D6E5}t$
which is, however, independent of the mesh size (Fernández and Zemzemi Reference Fernández and Zemzemi2010, Colli Franzone et al.
Reference Colli Franzone, Pavarino and Scacchi2014).
$\unicode[STIX]{x1D6E5}t$
which is, however, independent of the mesh size (Fernández and Zemzemi Reference Fernández and Zemzemi2010, Colli Franzone et al.
Reference Colli Franzone, Pavarino and Scacchi2014).
A variant of the semi-implicit method reported above arises from treating the reaction term
![]() $I_{\mathit{ion}}$
implicitly. In this case, Newton–Krylov–Schwarz methods are very efficient (Munteanu et al.
Reference Munteanu, Pavarino and Scacchi2009). Second-order semi-implicit schemes have been successfully considered as well: see e.g. Ethier and Bourgault (Reference Ethier and Bourgault2008).
$I_{\mathit{ion}}$
implicitly. In this case, Newton–Krylov–Schwarz methods are very efficient (Munteanu et al.
Reference Munteanu, Pavarino and Scacchi2009). Second-order semi-implicit schemes have been successfully considered as well: see e.g. Ethier and Bourgault (Reference Ethier and Bourgault2008).
Operator splitting-based methods.
These methods separate the reaction operator from the diffusive operator, in a similar way to what is done in fractional step methods for fluid problems. They were first introduced for the monodomain problem by Qu and Garfinkel (Reference Qu and Garfinkel1998). Here we present an operator splitting-based method for the PP formulation of the bidomain problem (Sundnes, Lines and Tveito Reference Sundnes, Lines and Tveito2005, Colli Franzone et al. Reference Colli Franzone, Pavarino and Scacchi2014).
-
(1) Given the quantities at time step
 $t^{n}$
, solve the reaction problem and the ODE systems in
$t^{n}$
, solve the reaction problem and the ODE systems in
 $(t^{n},t^{n}+\unicode[STIX]{x1D703}\unicode[STIX]{x1D6E5}t]$
:
$(t^{n},t^{n}+\unicode[STIX]{x1D703}\unicode[STIX]{x1D6E5}t]$
:  $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}_{m}C_{m}M\frac{\widetilde{\boldsymbol{V}}_{m}^{n+\unicode[STIX]{x1D703}}-\boldsymbol{V}_{m}^{n}}{\unicode[STIX]{x1D6E5}t}+\unicode[STIX]{x1D712}_{m}\boldsymbol{I}_{\mathit{ion}}(\boldsymbol{V}_{m}^{\ast },\boldsymbol{W}^{\ast },\boldsymbol{C}^{\ast }) & = & \displaystyle \mathbf{0},\nonumber\\ \displaystyle M\frac{\widetilde{\boldsymbol{W}}^{n+\unicode[STIX]{x1D703}}-\boldsymbol{W}^{n}}{\unicode[STIX]{x1D6E5}t}-\boldsymbol{G}(\boldsymbol{V}_{m}^{\ast },\boldsymbol{W}^{\ast }) & = & \displaystyle \mathbf{0},\nonumber\\ \displaystyle M\frac{\widetilde{\boldsymbol{C}}^{n+\unicode[STIX]{x1D703}}-\boldsymbol{C}^{n}}{\unicode[STIX]{x1D6E5}t}-\boldsymbol{S}(\boldsymbol{V}_{m}^{\ast },\boldsymbol{W}^{\ast },\boldsymbol{C}^{\ast }) & = & \displaystyle \mathbf{0}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}_{m}C_{m}M\frac{\widetilde{\boldsymbol{V}}_{m}^{n+\unicode[STIX]{x1D703}}-\boldsymbol{V}_{m}^{n}}{\unicode[STIX]{x1D6E5}t}+\unicode[STIX]{x1D712}_{m}\boldsymbol{I}_{\mathit{ion}}(\boldsymbol{V}_{m}^{\ast },\boldsymbol{W}^{\ast },\boldsymbol{C}^{\ast }) & = & \displaystyle \mathbf{0},\nonumber\\ \displaystyle M\frac{\widetilde{\boldsymbol{W}}^{n+\unicode[STIX]{x1D703}}-\boldsymbol{W}^{n}}{\unicode[STIX]{x1D6E5}t}-\boldsymbol{G}(\boldsymbol{V}_{m}^{\ast },\boldsymbol{W}^{\ast }) & = & \displaystyle \mathbf{0},\nonumber\\ \displaystyle M\frac{\widetilde{\boldsymbol{C}}^{n+\unicode[STIX]{x1D703}}-\boldsymbol{C}^{n}}{\unicode[STIX]{x1D6E5}t}-\boldsymbol{S}(\boldsymbol{V}_{m}^{\ast },\boldsymbol{W}^{\ast },\boldsymbol{C}^{\ast }) & = & \displaystyle \mathbf{0}.\nonumber\end{eqnarray}$$
-
(2) Given
 $\widetilde{\boldsymbol{V}}_{m}^{n+\unicode[STIX]{x1D703}}$
, solve the diffusion problems in
$\widetilde{\boldsymbol{V}}_{m}^{n+\unicode[STIX]{x1D703}}$
, solve the diffusion problems in
 $(t^{n},t^{n+1}]$
:
$(t^{n},t^{n+1}]$
:  $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}_{m}C_{m}M\frac{\widehat{\boldsymbol{V}}_{m}^{n+1}-\widetilde{\boldsymbol{V}}_{m}^{n+\unicode[STIX]{x1D703}}}{\unicode[STIX]{x1D6E5}t}+A_{i}\boldsymbol{\unicode[STIX]{x1D6F7}}_{i}^{\ast } & = & \displaystyle \mathbf{0},\nonumber\\ \displaystyle -\unicode[STIX]{x1D712}_{m}C_{m}M\frac{\widehat{\boldsymbol{V}}_{m}^{n+1}-\widetilde{\boldsymbol{V}}_{m}^{n+\unicode[STIX]{x1D703}}}{\unicode[STIX]{x1D6E5}t}+A_{e}\boldsymbol{\unicode[STIX]{x1D6F7}}_{e}^{\ast } & = & \displaystyle \mathbf{0}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}_{m}C_{m}M\frac{\widehat{\boldsymbol{V}}_{m}^{n+1}-\widetilde{\boldsymbol{V}}_{m}^{n+\unicode[STIX]{x1D703}}}{\unicode[STIX]{x1D6E5}t}+A_{i}\boldsymbol{\unicode[STIX]{x1D6F7}}_{i}^{\ast } & = & \displaystyle \mathbf{0},\nonumber\\ \displaystyle -\unicode[STIX]{x1D712}_{m}C_{m}M\frac{\widehat{\boldsymbol{V}}_{m}^{n+1}-\widetilde{\boldsymbol{V}}_{m}^{n+\unicode[STIX]{x1D703}}}{\unicode[STIX]{x1D6E5}t}+A_{e}\boldsymbol{\unicode[STIX]{x1D6F7}}_{e}^{\ast } & = & \displaystyle \mathbf{0}.\nonumber\end{eqnarray}$$
-
(3) Given
 $\widehat{\boldsymbol{V}}_{m}^{n+1},\,\widetilde{\boldsymbol{W}}^{n+\unicode[STIX]{x1D703}},\,\widetilde{\boldsymbol{C}}^{n+\unicode[STIX]{x1D703}}$
, solve the reaction problem and the ODE systems in
$\widehat{\boldsymbol{V}}_{m}^{n+1},\,\widetilde{\boldsymbol{W}}^{n+\unicode[STIX]{x1D703}},\,\widetilde{\boldsymbol{C}}^{n+\unicode[STIX]{x1D703}}$
, solve the reaction problem and the ODE systems in
 $(t^{n}+\unicode[STIX]{x1D703}\unicode[STIX]{x1D6E5}t,t^{n+1}]$
:
$(t^{n}+\unicode[STIX]{x1D703}\unicode[STIX]{x1D6E5}t,t^{n+1}]$
:  $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}_{m}C_{m}M\frac{\boldsymbol{V}_{m}^{n+1}-\widehat{\boldsymbol{V}}_{m}^{n+1}}{\unicode[STIX]{x1D6E5}t}+\unicode[STIX]{x1D712}_{m}\boldsymbol{I}_{\mathit{ion}}(\boldsymbol{V}_{m}^{\ast },\boldsymbol{W}^{\ast },\boldsymbol{C}^{\ast }) & = & \displaystyle \mathbf{0},\nonumber\\ \displaystyle M\frac{\boldsymbol{W}^{n+1}-\widetilde{\boldsymbol{W}}^{n+\unicode[STIX]{x1D703}}}{\unicode[STIX]{x1D6E5}t}-\boldsymbol{G}(\boldsymbol{V}_{m}^{\ast },\boldsymbol{W}^{\ast }) & = & \displaystyle \mathbf{0},\nonumber\\ \displaystyle M\frac{\boldsymbol{C}^{n+1}-\widetilde{\boldsymbol{C}}^{n+\unicode[STIX]{x1D703}}}{\unicode[STIX]{x1D6E5}t}-\boldsymbol{S}(\boldsymbol{V}_{m}^{\ast },\boldsymbol{W}^{\ast },\boldsymbol{C}^{\ast }) & = & \displaystyle \mathbf{0}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}_{m}C_{m}M\frac{\boldsymbol{V}_{m}^{n+1}-\widehat{\boldsymbol{V}}_{m}^{n+1}}{\unicode[STIX]{x1D6E5}t}+\unicode[STIX]{x1D712}_{m}\boldsymbol{I}_{\mathit{ion}}(\boldsymbol{V}_{m}^{\ast },\boldsymbol{W}^{\ast },\boldsymbol{C}^{\ast }) & = & \displaystyle \mathbf{0},\nonumber\\ \displaystyle M\frac{\boldsymbol{W}^{n+1}-\widetilde{\boldsymbol{W}}^{n+\unicode[STIX]{x1D703}}}{\unicode[STIX]{x1D6E5}t}-\boldsymbol{G}(\boldsymbol{V}_{m}^{\ast },\boldsymbol{W}^{\ast }) & = & \displaystyle \mathbf{0},\nonumber\\ \displaystyle M\frac{\boldsymbol{C}^{n+1}-\widetilde{\boldsymbol{C}}^{n+\unicode[STIX]{x1D703}}}{\unicode[STIX]{x1D6E5}t}-\boldsymbol{S}(\boldsymbol{V}_{m}^{\ast },\boldsymbol{W}^{\ast },\boldsymbol{C}^{\ast }) & = & \displaystyle \mathbf{0}.\nonumber\end{eqnarray}$$
The superscript
![]() $^{\ast }$
means that the quantity at hand could be treated either explicitly or implicitly. The variable
$^{\ast }$
means that the quantity at hand could be treated either explicitly or implicitly. The variable
![]() $\unicode[STIX]{x1D703}$
could assume value
$\unicode[STIX]{x1D703}$
could assume value
![]() $1/2$
or
$1/2$
or
![]() $1$
. In the latter case, step (3) is unnecessary: we set
$1$
. In the latter case, step (3) is unnecessary: we set
 $$\begin{eqnarray}\boldsymbol{V}_{m}^{n+1}=\widehat{\boldsymbol{V}}_{m}^{n+1},\quad \boldsymbol{W}^{n+1}=\widetilde{\boldsymbol{W}}^{n+1},\quad \boldsymbol{C}^{n+1}=\widetilde{\boldsymbol{C}}^{n+1},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{V}_{m}^{n+1}=\widehat{\boldsymbol{V}}_{m}^{n+1},\quad \boldsymbol{W}^{n+1}=\widetilde{\boldsymbol{W}}^{n+1},\quad \boldsymbol{C}^{n+1}=\widetilde{\boldsymbol{C}}^{n+1},\end{eqnarray}$$
and a first-order method is obtained (Godunov splitting). For
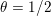 $\unicode[STIX]{x1D703}=1/2$
, we have a second-order method provided that all the subproblems are solved with a second-order strategy (Strang splitting). Note that if step (2) is solved implicitly, then the same preconditioners introduced above for the semi-implicit schemes could be applied as well, since it applies to the same operator.
$\unicode[STIX]{x1D703}=1/2$
, we have a second-order method provided that all the subproblems are solved with a second-order strategy (Strang splitting). Note that if step (2) is solved implicitly, then the same preconditioners introduced above for the semi-implicit schemes could be applied as well, since it applies to the same operator.
Implicit methods.
Some authors have considered a fully implicit discretization of the full bidomain problem (7.9): see e.g. Bourgault, Ethier and LeBlanc (Reference Bourgault, Ethier and Leblanc2003) and Murillo and Cai (Reference Murillo and Cai2004). In this case the whole Jacobian is built and the Newton method is applied. Due to the small time step required in bidomain simulations to capture the propagating front and due to the excellent stability properties of semi-implicit and operator splitting-based methods, fully implicit method are no longer considered so often.
In Figures 7.3 and 7.4 we give some examples of numerical results related to the solution of the electrical propagation in the myocardium.

Figure 7.3. (a) Purkinje network generated by the algorithm proposed in Palamara et al. (Reference Palamara, Vergara, Faggiano and Nobile2015) in the case of a real left ventricle. (b) Map of the activation times computed by means of the eikonal equation. The time marching scheme and P1 finite elements have been used. The source term (dark blue) is located within the myocardium, as typically happens in Wolff–Parkinson–White syndrome. Results were obtained by means of a code implemented in the VMTK environment (www.vmtk.org). CT images from the Cardiology Division at Ospedale S. Maria del Carmine, Rovereto (TN), Italy, and from the Radiology Division of Borgo-Trento (TN), Italy.

Figure 7.4. Propagation of the trans-membrane potential in the two ventricles at eight different instants during a heartbeat. Monodomain simulation, semi-implicit method, P1 finite elements. Results were obtained using LifeV; the computational mesh was obtained by an open source biventricular geometry segmented from CT images: see Rousseau (Reference Rousseau2010).
7.2 Cardiac mechanics and electromechanical coupling
7.2.1 The continuous mechanics problems
During a physiological contraction, the cardiac cells change in length by up to 20–30%, so finite elasticity models are needed to describe heart contraction and relaxation. In particular, the first Piola–Kirchhoff tensor is written as the sum of two terms (Nash and Panfilov Reference Nash and Panfilov2004, Niederer and Smith Reference Niederer and Smith2008): a passive component
![]() $\widehat{\boldsymbol{T}}_{s}^{P}$
describing the stress required to obtain a given deformation of the passive myocardium (similarly to arteries), and an active component
$\widehat{\boldsymbol{T}}_{s}^{P}$
describing the stress required to obtain a given deformation of the passive myocardium (similarly to arteries), and an active component
![]() $\widehat{\boldsymbol{T}}_{s}^{A}$
denoting the tension generated by the depolarization of the propagating electrical signal that provides the internal active forces responsible for the contraction (see Section 5.4):
$\widehat{\boldsymbol{T}}_{s}^{A}$
denoting the tension generated by the depolarization of the propagating electrical signal that provides the internal active forces responsible for the contraction (see Section 5.4):
 $$\begin{eqnarray}\widehat{\boldsymbol{T}}_{s}=\widehat{\boldsymbol{T}}_{s}^{P}+\widehat{\boldsymbol{T}}_{s}^{A},\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\boldsymbol{T}}_{s}=\widehat{\boldsymbol{T}}_{s}^{P}+\widehat{\boldsymbol{T}}_{s}^{A},\end{eqnarray}$$
where, using the notation of Part 1,
![]() $^{\widehat{~~~}}$
refers to quantities computed in the reference domain.
$^{\widehat{~~~}}$
refers to quantities computed in the reference domain.
The passive component of the stress is obtained as the derivative of a suitable strain energy function: see (4.8). The heart’s mechanical response (just like the electrical propagation: see Section 7.1) is highly dependent on the presence of fibres and sheets. For this reason, the passive myocardium is modelled as an orthotropic material, characterized by two principal directions and with different material responses on three mutually orthogonal planes, identified by these directions. This is in accordance with the shear tests performed on pig hearts, which highlighted an elevated resistance to shear deformations producing an extension along the fibre direction, an intermediate resistance in the direction orthogonal to fibres and tangential to sheets, and the least resistance in the third orthogonal direction (Dokos et al.
Reference Dokos, Smaill, Young and Legrice2002). Letting
![]() $\widehat{\boldsymbol{a}}_{f}$
,
$\widehat{\boldsymbol{a}}_{f}$
,
![]() $\widehat{\boldsymbol{a}}_{s}$
,
$\widehat{\boldsymbol{a}}_{s}$
,
![]() $\widehat{\boldsymbol{a}}_{n}$
denote the unit vectors along these directions (see Section 7.1) in the reference configuration, the following strain energy function has been proposed in Holzapfel and Ogden (Reference Holzapfel and Ogden2009):
$\widehat{\boldsymbol{a}}_{n}$
denote the unit vectors along these directions (see Section 7.1) in the reference configuration, the following strain energy function has been proposed in Holzapfel and Ogden (Reference Holzapfel and Ogden2009):
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D6E9}(I_{1},I_{4,f},I_{4,s},I_{8,fs})\nonumber\\ \displaystyle & & \displaystyle \displaystyle \qquad =\frac{a}{2b}\text{e}^{b(I_{1}-3)}+\mathop{\sum }_{i=f,s}\frac{a_{i}}{2b_{i}}[\text{e}^{b_{i}(I_{4,i}-1)^{2}}-1]+\frac{a_{fs}}{2b_{fs}}[\text{e}^{b_{fs}I_{8,fs}^{2}}-1],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D6E9}(I_{1},I_{4,f},I_{4,s},I_{8,fs})\nonumber\\ \displaystyle & & \displaystyle \displaystyle \qquad =\frac{a}{2b}\text{e}^{b(I_{1}-3)}+\mathop{\sum }_{i=f,s}\frac{a_{i}}{2b_{i}}[\text{e}^{b_{i}(I_{4,i}-1)^{2}}-1]+\frac{a_{fs}}{2b_{fs}}[\text{e}^{b_{fs}I_{8,fs}^{2}}-1],\end{eqnarray}$$
where, referring to the notation introduced in Section 4.2,
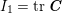 $I_{1}=\operatorname{tr}\boldsymbol{C}$
,
$I_{1}=\operatorname{tr}\boldsymbol{C}$
,
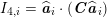 $I_{4,i}=\widehat{\boldsymbol{a}}_{i}\cdot (\boldsymbol{C}\widehat{\boldsymbol{a}}_{i})$
,
$I_{4,i}=\widehat{\boldsymbol{a}}_{i}\cdot (\boldsymbol{C}\widehat{\boldsymbol{a}}_{i})$
,
![]() $i=f,s$
,
$i=f,s$
,
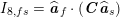 $I_{8,fs}=\widehat{\boldsymbol{a}}_{f}\cdot (\boldsymbol{C}\widehat{\boldsymbol{a}}_{s})$
are invariants of
$I_{8,fs}=\widehat{\boldsymbol{a}}_{f}\cdot (\boldsymbol{C}\widehat{\boldsymbol{a}}_{s})$
are invariants of
![]() $\boldsymbol{C}$
, and
$\boldsymbol{C}$
, and
![]() $a$
,
$a$
,
![]() $b$
,
$b$
,
![]() $a_{f}$
,
$a_{f}$
,
![]() $b_{f}$
,
$b_{f}$
,
![]() $a_{s}$
,
$a_{s}$
,
![]() $b_{s}$
,
$b_{s}$
,
![]() $a_{fs}$
,
$a_{fs}$
,
![]() $b_{fs}$
are material parameters.
$b_{fs}$
are material parameters.
![]() $I_{1}$
is the first isotropic invariant and the related term in
$I_{1}$
is the first isotropic invariant and the related term in
![]() $\unicode[STIX]{x1D6E9}$
accounts for the isotropic response of the myocardium at small deformations;
$\unicode[STIX]{x1D6E9}$
accounts for the isotropic response of the myocardium at small deformations;
![]() $I_{4,f}$
and
$I_{4,f}$
and
![]() $I_{4,s}$
are the squares of the stretch of
$I_{4,s}$
are the squares of the stretch of
![]() $\widehat{\boldsymbol{a}}_{f}$
and
$\widehat{\boldsymbol{a}}_{f}$
and
![]() $\widehat{\boldsymbol{a}}_{s}$
in the deformed configuration, and the related terms in the energy are associated with the increased stiffness of the material along the two principal directions
$\widehat{\boldsymbol{a}}_{s}$
in the deformed configuration, and the related terms in the energy are associated with the increased stiffness of the material along the two principal directions
![]() $\boldsymbol{a}_{f}$
and
$\boldsymbol{a}_{f}$
and
![]() $\boldsymbol{a}_{s}$
for large deformations; finally,
$\boldsymbol{a}_{s}$
for large deformations; finally,
![]() $I_{8,fs}$
denotes the angle spanned by the two principal directions in the deformed configuration, and the related term in the energy describes the coupling between the two principal directions. Convexity of this energy is guaranteed for positive parameter values (Holzapfel and Ogden Reference Holzapfel and Ogden2009). Other orthotropic models have been proposed, for example by Hunter, Nash and Sands (Reference Hunter, Nash, Sands, Panfilov and Holden1997) and Costa, Holmes and McCulloch (Reference Costa, Holmes and Mcculloch2001), whereas transversally isotropic models with only one principal direction (along the fibres) were introduced by Humphrey and Yin (Reference Humphrey and Yin1987) and Guccione, McCulloch and Waldman (Reference Guccione, Mcculloch and Waldman1991), for example. Some authors model the myocardium as incompressible (Holzapfel and Ogden Reference Holzapfel and Ogden2009), in accordance with the experiments reported by Vossoughi, Vaishnav and Patel (Reference Vossoughi, Vaishnav, Patel and Mow1980). In this case the term
$I_{8,fs}$
denotes the angle spanned by the two principal directions in the deformed configuration, and the related term in the energy describes the coupling between the two principal directions. Convexity of this energy is guaranteed for positive parameter values (Holzapfel and Ogden Reference Holzapfel and Ogden2009). Other orthotropic models have been proposed, for example by Hunter, Nash and Sands (Reference Hunter, Nash, Sands, Panfilov and Holden1997) and Costa, Holmes and McCulloch (Reference Costa, Holmes and Mcculloch2001), whereas transversally isotropic models with only one principal direction (along the fibres) were introduced by Humphrey and Yin (Reference Humphrey and Yin1987) and Guccione, McCulloch and Waldman (Reference Guccione, Mcculloch and Waldman1991), for example. Some authors model the myocardium as incompressible (Holzapfel and Ogden Reference Holzapfel and Ogden2009), in accordance with the experiments reported by Vossoughi, Vaishnav and Patel (Reference Vossoughi, Vaishnav, Patel and Mow1980). In this case the term
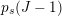 $p_{s}(J-1)$
is added to the strain energy functions, as in (4.13).
$p_{s}(J-1)$
is added to the strain energy functions, as in (4.13).
On the basis of experimental evidence, reported by Dokos et al. (Reference Dokos, Smaill, Young and Legrice2002), for example, highlighting hysteresis under shear deformations, viscoelastic orthotropic models have recently been proposed for the passive myocardium: see Gultekin, Sommer and Holzapfel (Reference Gultekin, Sommer and Holzapfel2016). The viscoelastic behaviour is probably due to the extracellular fluid that filtrates through the solid part.
The active contribution of the cardiac cells to the contraction is regulated by the opening of calcium channels as a response to the depolarization, with a consequent entry of calcium ions in the cells. As detailed in Section 5.4, this process is responsible for cardiac contraction. Since the latter occurs along the axial direction of the cardiac cells, that is, along the fibre direction, the active part of the stress tensor usually takes the form
 $$\begin{eqnarray}\widehat{\boldsymbol{T}}_{s}^{A}=P^{A}\boldsymbol{a}_{f}\otimes \widehat{\boldsymbol{a}}_{f}\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\boldsymbol{T}}_{s}^{A}=P^{A}\boldsymbol{a}_{f}\otimes \widehat{\boldsymbol{a}}_{f}\end{eqnarray}$$
(Nash and Panfilov Reference Nash and Panfilov2004), where the scalar function of time and space
![]() $P^{A}$
denotes the pointwise active stress, and should be properly modelled.
$P^{A}$
denotes the pointwise active stress, and should be properly modelled.
In the classical model for the active stress function proposed in Nash and Panfilov (Reference Nash and Panfilov2004),
![]() $P^{A}$
depends only on the trans-membrane potential
$P^{A}$
depends only on the trans-membrane potential
![]() $V_{m}$
. In particular, for each spatial point, the following ODE equation is introduced:
$V_{m}$
. In particular, for each spatial point, the following ODE equation is introduced:
 $$\begin{eqnarray}\frac{\text{d}P^{A}(t)}{\text{d}t}=\unicode[STIX]{x1D700}(V_{m}(t))[k_{P}(V_{m}(t)-V_{r})-P^{A}(t)],\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}P^{A}(t)}{\text{d}t}=\unicode[STIX]{x1D700}(V_{m}(t))[k_{P}(V_{m}(t)-V_{r})-P^{A}(t)],\end{eqnarray}$$
where
![]() $V_{r}$
is the resting potential,
$V_{r}$
is the resting potential,
![]() $k_{P}$
is a suitable parameter controlling the amplitude of
$k_{P}$
is a suitable parameter controlling the amplitude of
![]() $P^{A}$
, and
$P^{A}$
, and
![]() $\unicode[STIX]{x1D700}$
controls the delay of the contraction with respect to the action potential. For example, Goktepe and Kuhl (Reference Goktepe and Kuhl2010) proposed the expression
$\unicode[STIX]{x1D700}$
controls the delay of the contraction with respect to the action potential. For example, Goktepe and Kuhl (Reference Goktepe and Kuhl2010) proposed the expression
 $$\begin{eqnarray}\unicode[STIX]{x1D700}(V_{m})=\unicode[STIX]{x1D700}_{0}+(\unicode[STIX]{x1D700}_{\infty }-\unicode[STIX]{x1D700}_{0})\text{e}^{-\text{e}^{-\unicode[STIX]{x1D709}(V_{m}-\bar{V}_{m})}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D700}(V_{m})=\unicode[STIX]{x1D700}_{0}+(\unicode[STIX]{x1D700}_{\infty }-\unicode[STIX]{x1D700}_{0})\text{e}^{-\text{e}^{-\unicode[STIX]{x1D709}(V_{m}-\bar{V}_{m})}},\end{eqnarray}$$
where
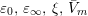 $\unicode[STIX]{x1D700}_{0},\,\unicode[STIX]{x1D700}_{\infty },\,\unicode[STIX]{x1D709},\,\bar{V}_{m}$
are suitable parameters.
$\unicode[STIX]{x1D700}_{0},\,\unicode[STIX]{x1D700}_{\infty },\,\unicode[STIX]{x1D709},\,\bar{V}_{m}$
are suitable parameters.
Since cardiac cell contraction is regulated by calcium ion concentration, the active stress function
![]() $P^{A}$
can be assumed to depend directly on this specific concentration, say
$P^{A}$
can be assumed to depend directly on this specific concentration, say
![]() $c_{ca}$
, rather than on the more general variable
$c_{ca}$
, rather than on the more general variable
![]() $V_{m}$
. For example, Wong et al. (Reference Wong, Goktepe and Kuhl2013) proposed a system of ODEs of the same structure as (7.26), but using
$V_{m}$
. For example, Wong et al. (Reference Wong, Goktepe and Kuhl2013) proposed a system of ODEs of the same structure as (7.26), but using
![]() $c_{ca}$
instead of
$c_{ca}$
instead of
![]() $V_{m}$
on the right-hand side.
$V_{m}$
on the right-hand side.
In more sophisticated models, the active stress function also depends on the stretch in the fibre direction
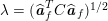 $\unicode[STIX]{x1D706}=(\widehat{\boldsymbol{a}}_{f}^{T}C\widehat{\boldsymbol{a}}_{f})^{1/2}$
and on the fibre stretch rate
$\unicode[STIX]{x1D706}=(\widehat{\boldsymbol{a}}_{f}^{T}C\widehat{\boldsymbol{a}}_{f})^{1/2}$
and on the fibre stretch rate
![]() $\text{d}\unicode[STIX]{x1D706}/\text{d}t$
(Niederer, Hunter and Smith Reference Niederer, Hunter and Smith2006, Land et al.
Reference Land, Niederer, Aronsen, Espe, Zhang, Louch, Sjaastad, Sejersted and Smith2012). In compact form, these models are written as
$\text{d}\unicode[STIX]{x1D706}/\text{d}t$
(Niederer, Hunter and Smith Reference Niederer, Hunter and Smith2006, Land et al.
Reference Land, Niederer, Aronsen, Espe, Zhang, Louch, Sjaastad, Sejersted and Smith2012). In compact form, these models are written as
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}rcl@{}}\frac{\text{d}\boldsymbol{y}}{\text{d}t}\; & =\; & \boldsymbol{g}_{y}\biggl(P^{A},\unicode[STIX]{x1D706},\frac{\text{d}\unicode[STIX]{x1D706}}{\text{d}t},\boldsymbol{c},\boldsymbol{y}\biggr),\\ P^{A}\; & =\; & g_{P^{A}}(\unicode[STIX]{x1D706},\boldsymbol{y}),\end{array} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}rcl@{}}\frac{\text{d}\boldsymbol{y}}{\text{d}t}\; & =\; & \boldsymbol{g}_{y}\biggl(P^{A},\unicode[STIX]{x1D706},\frac{\text{d}\unicode[STIX]{x1D706}}{\text{d}t},\boldsymbol{c},\boldsymbol{y}\biggr),\\ P^{A}\; & =\; & g_{P^{A}}(\unicode[STIX]{x1D706},\boldsymbol{y}),\end{array} & & \displaystyle\end{eqnarray}$$
for suitable functions
![]() $\boldsymbol{g}_{y}$
and
$\boldsymbol{g}_{y}$
and
![]() $g_{P^{A}}$
and where
$g_{P^{A}}$
and where
![]() $\boldsymbol{c}$
, as in Section 7.1, is the ionic concentration variable (in particular the calcium one), whereas
$\boldsymbol{c}$
, as in Section 7.1, is the ionic concentration variable (in particular the calcium one), whereas
![]() $\boldsymbol{y}$
collects other myofilament and electrophysiology state variables.
$\boldsymbol{y}$
collects other myofilament and electrophysiology state variables.
As an alternative to the decomposition (7.23), where the stress tensor is split into a passive and an active component (the active stress approach), Cherubini et al. (Reference Cherubini, Filippi, Nardinocchi and Teresi2008) and Ambrosi et al. (Reference Ambrosi, Arioli, Nobile and Quarteroni2011) have proposed a different strategy based on an active strain approach. In this case, the following factorization of the deformation tensor is used,
 $$\begin{eqnarray}\boldsymbol{F}=\boldsymbol{F}^{P}\boldsymbol{F}^{A},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{F}=\boldsymbol{F}^{P}\boldsymbol{F}^{A},\end{eqnarray}$$
where
![]() $\boldsymbol{F}^{A}$
is the active factor acting at the microscales, describing fibre distortion not preserving geometric compatibility, whereas
$\boldsymbol{F}^{A}$
is the active factor acting at the microscales, describing fibre distortion not preserving geometric compatibility, whereas
![]() $\boldsymbol{F}^{P}$
describes passive macroscale deformation and the deformation needed to restore compatibility. With this choice, quite common when analysing plasticity and the remodelling of living tissues, the microscale information related to the fibre contraction is directly incorporated in the body kinematics, allowing for the inclusion of fibre contraction driven by the depolarization as a prescribed active deformation rather than a further contribution to stress. In this case, the first Piola–Kirchhoff stress tensor is given by
$\boldsymbol{F}^{P}$
describes passive macroscale deformation and the deformation needed to restore compatibility. With this choice, quite common when analysing plasticity and the remodelling of living tissues, the microscale information related to the fibre contraction is directly incorporated in the body kinematics, allowing for the inclusion of fibre contraction driven by the depolarization as a prescribed active deformation rather than a further contribution to stress. In this case, the first Piola–Kirchhoff stress tensor is given by
 $$\begin{eqnarray}\widehat{\boldsymbol{T}}_{s}=J^{A}\frac{D\unicode[STIX]{x1D6E9}}{D\boldsymbol{F}^{P}}(\boldsymbol{F}^{A})^{-T},\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\boldsymbol{T}}_{s}=J^{A}\frac{D\unicode[STIX]{x1D6E9}}{D\boldsymbol{F}^{P}}(\boldsymbol{F}^{A})^{-T},\end{eqnarray}$$
and, in analogy with (7.25), a possible expression for
![]() $\boldsymbol{F}^{A}$
is
$\boldsymbol{F}^{A}$
is
 $$\begin{eqnarray}\boldsymbol{F}^{A}=\boldsymbol{I}-\unicode[STIX]{x1D6FD}V_{m}\widehat{\boldsymbol{a}}_{f}\otimes \widehat{\boldsymbol{a}}_{f},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{F}^{A}=\boldsymbol{I}-\unicode[STIX]{x1D6FD}V_{m}\widehat{\boldsymbol{a}}_{f}\otimes \widehat{\boldsymbol{a}}_{f},\end{eqnarray}$$
for a suitable parameter
![]() $\unicode[STIX]{x1D6FD}$
(Ambrosi et al.
Reference Ambrosi, Arioli, Nobile and Quarteroni2011). The active strain approach is probably more satisfactory from the modelling point of view, since, unlike active stress, it should provide the expected fibre contraction without any tuning. However, from the numerical point of view it is more problematic, since standard finite element finite elasticity solvers cannot be used directly and should be properly adapted. From now on we refer only to the active stress approach. For a comparison between the two approaches we refer to Ambrosi et al. (Reference Ambrosi, Arioli, Nobile and Quarteroni2011) and Ambrosi and Pezzuto (Reference Ambrosi and Pezzuto2012), and for related computational results to Pezzuto (Reference Pezzuto2013) and Rossi et al. (Reference Rossi, Lassila, Ruiz-Baier, Sequeira and Quarteroni2014).
$\unicode[STIX]{x1D6FD}$
(Ambrosi et al.
Reference Ambrosi, Arioli, Nobile and Quarteroni2011). The active strain approach is probably more satisfactory from the modelling point of view, since, unlike active stress, it should provide the expected fibre contraction without any tuning. However, from the numerical point of view it is more problematic, since standard finite element finite elasticity solvers cannot be used directly and should be properly adapted. From now on we refer only to the active stress approach. For a comparison between the two approaches we refer to Ambrosi et al. (Reference Ambrosi, Arioli, Nobile and Quarteroni2011) and Ambrosi and Pezzuto (Reference Ambrosi and Pezzuto2012), and for related computational results to Pezzuto (Reference Pezzuto2013) and Rossi et al. (Reference Rossi, Lassila, Ruiz-Baier, Sequeira and Quarteroni2014).
7.2.2 The coupled electromechanics problem
The values of the trans-membrane potential
![]() $V_{m}$
or calcium ion concentration
$V_{m}$
or calcium ion concentration
![]() $c_{ca}$
, to be used in (7.26) or (7.27) to compute the active stress function
$c_{ca}$
, to be used in (7.26) or (7.27) to compute the active stress function
![]() $P^{A}$
, are sometimes prescribed as given data to the mechanics problem: see e.g. Eriksson et al. (Reference Eriksson, Prassl, Plank and Holzapfel2013). However, in most cases they are obtained from the bidomain or monodomain equations. This leads to a coupled electromechanical problem.
$P^{A}$
, are sometimes prescribed as given data to the mechanics problem: see e.g. Eriksson et al. (Reference Eriksson, Prassl, Plank and Holzapfel2013). However, in most cases they are obtained from the bidomain or monodomain equations. This leads to a coupled electromechanical problem.
The electrical propagation problem needs to be solved in a domain that changes in time, because of the cardiac contraction and relaxation. Under suitable assumptions (Colli Franzone, Pavarino and Scacchi Reference Colli Franzone, Pavarino and Scacchi2016), in an Eulerian framework, these problems assume the form (7.5), (7.6) or (7.11), provided that the conductivity tensors (7.4) or (7.12) are computed by using the deformed unit directions
 $\boldsymbol{a}_{f},\,\boldsymbol{a}_{s},\,\boldsymbol{a}_{n}$
: see e.g. Keldermann et al. (Reference Keldermann, Nash and Panfilov2009). However, for computational simplicity, the bidomain and monodomain equations are usually set in a Lagrangian framework and written in the reference undeformed configuration. Here we report the corresponding monodomain equation,
$\boldsymbol{a}_{f},\,\boldsymbol{a}_{s},\,\boldsymbol{a}_{n}$
: see e.g. Keldermann et al. (Reference Keldermann, Nash and Panfilov2009). However, for computational simplicity, the bidomain and monodomain equations are usually set in a Lagrangian framework and written in the reference undeformed configuration. Here we report the corresponding monodomain equation,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle J\unicode[STIX]{x1D712}_{m}C_{m}\biggl(\frac{\unicode[STIX]{x2202}\widehat{V}_{m}}{\unicode[STIX]{x2202}t}-\boldsymbol{F}^{-T}\unicode[STIX]{x1D6FB}\widehat{V}_{m}\cdot \frac{\unicode[STIX]{x2202}\boldsymbol{\unicode[STIX]{x1D713}}}{\unicode[STIX]{x2202}t}\biggr)-\unicode[STIX]{x1D6FB}\cdot (J\boldsymbol{F}^{-1}\boldsymbol{\unicode[STIX]{x1D6F4}}\boldsymbol{F}^{-T}\unicode[STIX]{x1D6FB}\widehat{V}_{m})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,J\unicode[STIX]{x1D712}_{m}\widetilde{I}_{\mathit{ion}}(\widehat{V}_{m},\widehat{\boldsymbol{w}},\widehat{\boldsymbol{c}},\unicode[STIX]{x1D706})=J\widehat{I}^{\mathit{ext}}\quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle J\unicode[STIX]{x1D712}_{m}C_{m}\biggl(\frac{\unicode[STIX]{x2202}\widehat{V}_{m}}{\unicode[STIX]{x2202}t}-\boldsymbol{F}^{-T}\unicode[STIX]{x1D6FB}\widehat{V}_{m}\cdot \frac{\unicode[STIX]{x2202}\boldsymbol{\unicode[STIX]{x1D713}}}{\unicode[STIX]{x2202}t}\biggr)-\unicode[STIX]{x1D6FB}\cdot (J\boldsymbol{F}^{-1}\boldsymbol{\unicode[STIX]{x1D6F4}}\boldsymbol{F}^{-T}\unicode[STIX]{x1D6FB}\widehat{V}_{m})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,J\unicode[STIX]{x1D712}_{m}\widetilde{I}_{\mathit{ion}}(\widehat{V}_{m},\widehat{\boldsymbol{w}},\widehat{\boldsymbol{c}},\unicode[STIX]{x1D706})=J\widehat{I}^{\mathit{ext}}\quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}\end{eqnarray}$$
(using the notation of Part 1, we set
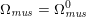 $\unicode[STIX]{x1D6FA}_{\mathit{mus}}=\unicode[STIX]{x1D6FA}_{\mathit{mus}}^{0}$
), coupled with the ODE systems (7.9e
, 7.9f
) (similar arguments hold true for the bidomain equations as well). The spatial derivatives have to be taken with respect to the undeformed domain,
$\unicode[STIX]{x1D6FA}_{\mathit{mus}}=\unicode[STIX]{x1D6FA}_{\mathit{mus}}^{0}$
), coupled with the ODE systems (7.9e
, 7.9f
) (similar arguments hold true for the bidomain equations as well). The spatial derivatives have to be taken with respect to the undeformed domain,
![]() $\boldsymbol{\unicode[STIX]{x1D713}}$
is the deformation map between
$\boldsymbol{\unicode[STIX]{x1D713}}$
is the deformation map between
![]() $\unicode[STIX]{x1D6FA}_{\mathit{mus}}^{0}$
and
$\unicode[STIX]{x1D6FA}_{\mathit{mus}}^{0}$
and
![]() $\unicode[STIX]{x1D6FA}_{\mathit{mus}}^{t}$
and
$\unicode[STIX]{x1D6FA}_{\mathit{mus}}^{t}$
and
![]() $\unicode[STIX]{x1D706}$
is the stretch in the fibre direction introduced above.
$\unicode[STIX]{x1D706}$
is the stretch in the fibre direction introduced above.
From the above equation, we observe that there are three sources of mechano-electrical feedback, that is, three ways in which the mechanics problem influences the electrical problem:
-
(i) the effective conductivity tensor
 $\widehat{\boldsymbol{\unicode[STIX]{x1D6F4}}}=J\boldsymbol{F}^{-1}\boldsymbol{\unicode[STIX]{x1D6F4}}\boldsymbol{F}^{-T}$
depends on the deformation gradient
$\widehat{\boldsymbol{\unicode[STIX]{x1D6F4}}}=J\boldsymbol{F}^{-1}\boldsymbol{\unicode[STIX]{x1D6F4}}\boldsymbol{F}^{-T}$
depends on the deformation gradient
 $\boldsymbol{F}$
,
$\boldsymbol{F}$
, -
(ii) the ionic current term
 $I_{\mathit{ion}}$
depends on the stretch in the fibre direction
$I_{\mathit{ion}}$
depends on the stretch in the fibre direction
 $\unicode[STIX]{x1D706}$
,
$\unicode[STIX]{x1D706}$
, -
(iii) the relation between the spatial and material time derivatives introduces the advection term
 $-\boldsymbol{F}^{-T}\unicode[STIX]{x1D6FB}\widehat{V}_{m}\cdot \unicode[STIX]{x2202}\boldsymbol{\unicode[STIX]{x1D713}}/\unicode[STIX]{x2202}t$
, which depends on the solution of the mechanics problem (Colli Franzone et al.
Reference Colli Franzone, Pavarino and Scacchi2016).
$-\boldsymbol{F}^{-T}\unicode[STIX]{x1D6FB}\widehat{V}_{m}\cdot \unicode[STIX]{x2202}\boldsymbol{\unicode[STIX]{x1D713}}/\unicode[STIX]{x2202}t$
, which depends on the solution of the mechanics problem (Colli Franzone et al.
Reference Colli Franzone, Pavarino and Scacchi2016).
Terms (i) and (iii) are due to the pull-back of the monodomain equation into the undeformed domain (geometric feedback). Term (ii) is due to a well-known physical process consisting of the opening of ion channels under the action of deformation (stretch-activated channels: see Section 5.4) (Kohl, Hunter and Noble Reference Kohl, Hunter and Noble1999, Kohl and Sachs Reference Kohl and Sachs2001). Accordingly, the ionic current term is written as the sum of two contributions,
 $$\begin{eqnarray}\widetilde{I}_{\mathit{ion}}=I_{\mathit{ion}}(\widehat{V}_{m},\widehat{\boldsymbol{w}},\widehat{\boldsymbol{c}})+I^{\mathit{SAC}}(\widehat{V}_{m},\unicode[STIX]{x1D706}),\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{I}_{\mathit{ion}}=I_{\mathit{ion}}(\widehat{V}_{m},\widehat{\boldsymbol{w}},\widehat{\boldsymbol{c}})+I^{\mathit{SAC}}(\widehat{V}_{m},\unicode[STIX]{x1D706}),\end{eqnarray}$$
where
![]() $I_{\mathit{ion}}$
denotes one of the classical independent-stretch models described in Section 7.1.2, and
$I_{\mathit{ion}}$
denotes one of the classical independent-stretch models described in Section 7.1.2, and
![]() $I^{\mathit{SAC}}$
is the current activated by the deformation. A fairly general expression for the latter term is given by
$I^{\mathit{SAC}}$
is the current activated by the deformation. A fairly general expression for the latter term is given by
 $$\begin{eqnarray}I^{\mathit{SAC}}=\mathop{\sum }_{i}K_{i}(\widehat{V}_{m})(\unicode[STIX]{x1D706}-1)(\widehat{V}_{m}-V_{i})H(\unicode[STIX]{x1D706}-1),\end{eqnarray}$$
$$\begin{eqnarray}I^{\mathit{SAC}}=\mathop{\sum }_{i}K_{i}(\widehat{V}_{m})(\unicode[STIX]{x1D706}-1)(\widehat{V}_{m}-V_{i})H(\unicode[STIX]{x1D706}-1),\end{eqnarray}$$
where the
![]() $i$
th term of the sum represents the stretch-activated currents related to the
$i$
th term of the sum represents the stretch-activated currents related to the
![]() $i$
th ion (usually sodium and potassium),
$i$
th ion (usually sodium and potassium),
![]() $K_{i}$
is a suitable function, and
$K_{i}$
is a suitable function, and
![]() $V_{i}$
is the Nerst potential introduced in Section 7.1.2. The Heaviside function
$V_{i}$
is the Nerst potential introduced in Section 7.1.2. The Heaviside function
![]() $H(\cdot )$
guarantees that the stretch-activated ion channels open only under fibre tension (
$H(\cdot )$
guarantees that the stretch-activated ion channels open only under fibre tension (
![]() $\unicode[STIX]{x1D706}>1$
) (Niederer and Smith Reference Niederer and Smith2007). Colli Franzone et al. (Reference Colli Franzone, Pavarino and Scacchi2016) showed (computationally) that these terms do not significantly alter the morphology of the action potential, but they strongly influence the action potential duration.
$\unicode[STIX]{x1D706}>1$
) (Niederer and Smith Reference Niederer and Smith2007). Colli Franzone et al. (Reference Colli Franzone, Pavarino and Scacchi2016) showed (computationally) that these terms do not significantly alter the morphology of the action potential, but they strongly influence the action potential duration.
Stretch-activated ionic currents together with the active stress component of the stress tensor (or equivalently the active strain component of the deformation gradient) make the electromechanics problem a highly coupled system, which can be summarized as follows. Find the muscle displacement
![]() $\boldsymbol{d}$
, the trans-membrane potential
$\boldsymbol{d}$
, the trans-membrane potential
![]() $V_{m}$
, the gating variables
$V_{m}$
, the gating variables
![]() $\boldsymbol{w}$
, and the ionic concentration variables
$\boldsymbol{w}$
, and the ionic concentration variables
![]() $\boldsymbol{c}$
, such that
$\boldsymbol{c}$
, such that
 $$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D6FB}\cdot \biggl(\widehat{\boldsymbol{T}}_{s}^{P}(\widehat{\boldsymbol{d}})+\widehat{\boldsymbol{T}}_{s}^{A}\biggl(\widehat{\boldsymbol{c}},\widehat{\boldsymbol{d}},\frac{\text{d}\widehat{\boldsymbol{d}}}{\text{d}t}\biggr)\biggr)=\mathbf{0} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D6FB}\cdot \biggl(\widehat{\boldsymbol{T}}_{s}^{P}(\widehat{\boldsymbol{d}})+\widehat{\boldsymbol{T}}_{s}^{A}\biggl(\widehat{\boldsymbol{c}},\widehat{\boldsymbol{d}},\frac{\text{d}\widehat{\boldsymbol{d}}}{\text{d}t}\biggr)\biggr)=\mathbf{0} & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle \widehat{\boldsymbol{T}}_{s}^{A}=P^{A}\boldsymbol{a}_{f}\otimes \widehat{\boldsymbol{a}}_{f},\quad P^{A}={\mathcal{A}}\biggl(\widehat{\boldsymbol{c}},\widehat{\boldsymbol{d}},\frac{\text{d}\widehat{\boldsymbol{d}}}{\text{d}t}\biggr) & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \widehat{\boldsymbol{T}}_{s}^{A}=P^{A}\boldsymbol{a}_{f}\otimes \widehat{\boldsymbol{a}}_{f},\quad P^{A}={\mathcal{A}}\biggl(\widehat{\boldsymbol{c}},\widehat{\boldsymbol{d}},\frac{\text{d}\widehat{\boldsymbol{d}}}{\text{d}t}\biggr) & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle \widehat{V}_{m}={\mathcal{M}}(\widehat{V}_{m};\widehat{\boldsymbol{d}},\widehat{\boldsymbol{w}},\widehat{\boldsymbol{c}}) & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \widehat{V}_{m}={\mathcal{M}}(\widehat{V}_{m};\widehat{\boldsymbol{d}},\widehat{\boldsymbol{w}},\widehat{\boldsymbol{c}}) & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle (\widehat{\boldsymbol{w}},\widehat{\boldsymbol{c}})={\mathcal{G}}(\widehat{\boldsymbol{w}},\widehat{\boldsymbol{c}};\widehat{V}_{m}) & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle (\widehat{\boldsymbol{w}},\widehat{\boldsymbol{c}})={\mathcal{G}}(\widehat{\boldsymbol{w}},\widehat{\boldsymbol{c}};\widehat{V}_{m}) & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}.\end{eqnarray}$$
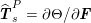 $\widehat{\boldsymbol{T}}_{s}^{P}=\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}/\unicode[STIX]{x2202}\boldsymbol{F}$
, where
$\widehat{\boldsymbol{T}}_{s}^{P}=\unicode[STIX]{x2202}\unicode[STIX]{x1D6E9}/\unicode[STIX]{x2202}\boldsymbol{F}$
, where
Regarding the well-posedness of the electromechanical coupled problem (7.31), very few results have been obtained so far. We mention Pathmanathan et al. (Reference Pathmanathan, Chapman, Gavaghan and Whiteley2010), who noticed that for the general active stress model (7.27), the equilibrium equation (7.31a
) is not even elliptic when there is explicit dependence on the rate of stretch
![]() $\text{d}\unicode[STIX]{x1D706}/\text{d}t$
, and Andreianov et al. (Reference Andreianov, Bendahmane, Quarteroni and Ruiz-Baier2015), who proved the existence of a weak solution for the case of a linearized elasticity equation in the active strain formulation coupled with the bidomain equations including the geometric feedback affecting the conductivity tensors.
$\text{d}\unicode[STIX]{x1D706}/\text{d}t$
, and Andreianov et al. (Reference Andreianov, Bendahmane, Quarteroni and Ruiz-Baier2015), who proved the existence of a weak solution for the case of a linearized elasticity equation in the active strain formulation coupled with the bidomain equations including the geometric feedback affecting the conductivity tensors.
7.2.3 The issue of boundary conditions for the mechanics problem
For the mechanical contraction problem (7.31a
), proper boundary conditions should be prescribed at both the external epicardium and internal endocardium surfaces. For the former, the presence of both the pericardium and the surrounding tissue has to be accounted for, because of their effect on heart movement. Fritz et al. (Reference Fritz, Wieners, Seemann, Steen and Dossel2014) have proposed a sophisticated model of interaction with the pericardium accounting for a frictionless contact. More commonly, and similarly to the vascular case, a Robin condition such as (3.1) is prescribed at
![]() $\unicode[STIX]{x1D6F4}_{\mathit{epi}}$
.
$\unicode[STIX]{x1D6F4}_{\mathit{epi}}$
.
At the endocardium internal surface
![]() $\unicode[STIX]{x1D6F4}_{\mathit{endo}}$
, in the presence of a fluid model in the atrial and ventricular cavities, the usual dynamic and kinematic conditions (4.19c
, 4.19d
), arising from the fluid–structure interaction model, implicitly provide both the endocardial displacement and normal stresses (see Section 7.5). When the fluid in the ventricular cavity is not modelled, suitable strategies to prescribe boundary conditions at
$\unicode[STIX]{x1D6F4}_{\mathit{endo}}$
, in the presence of a fluid model in the atrial and ventricular cavities, the usual dynamic and kinematic conditions (4.19c
, 4.19d
), arising from the fluid–structure interaction model, implicitly provide both the endocardial displacement and normal stresses (see Section 7.5). When the fluid in the ventricular cavity is not modelled, suitable strategies to prescribe boundary conditions at
![]() $\unicode[STIX]{x1D6F4}_{\mathit{endo}}$
are mandatory. A common strategy relies on prescribing a Neumann condition of the form
$\unicode[STIX]{x1D6F4}_{\mathit{endo}}$
are mandatory. A common strategy relies on prescribing a Neumann condition of the form
 $$\begin{eqnarray}\widehat{\boldsymbol{T}}_{s}\widehat{\boldsymbol{n}}=P\widehat{\boldsymbol{n}},\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\boldsymbol{T}}_{s}\widehat{\boldsymbol{n}}=P\widehat{\boldsymbol{n}},\end{eqnarray}$$
where
![]() $P$
is a suitable estimate of the blood pressure distribution at the endocardium.
$P$
is a suitable estimate of the blood pressure distribution at the endocardium.
During ventricular filling, condition (7.32) is prescribed both for atria and ventricles by means of selected values of blood pressures taken from the literature (see Figure 5.2).
During isovolumic contraction, the ventricular volume is kept constant by means of fixed-point iterations, for example, where the value of the endocardial pressure to be prescribed in (7.32) at each time step is updated until satisfaction of the constraint given by the unchanged volume:
 $$\begin{eqnarray}P_{(k+1)}=P_{(k)}+(V-V^{n})/C_{k}\end{eqnarray}$$
$$\begin{eqnarray}P_{(k+1)}=P_{(k)}+(V-V^{n})/C_{k}\end{eqnarray}$$
(Usyk, LeGrice and McCulloch Reference Usyk, Legrice and Mcculloch2002, Eriksson et al.
Reference Eriksson, Prassl, Plank and Holzapfel2013), where
![]() $V$
is the cavity volume,
$V$
is the cavity volume,
![]() $k$
is the sub-iteration index and
$k$
is the sub-iteration index and
![]() $C_{k}$
is a penalty parameter, and where the current temporal index
$C_{k}$
is a penalty parameter, and where the current temporal index
![]() $^{n+1}$
is as usual understood. Alternatively, a Lagrange multiplier approach could be employed (Gurev et al.
Reference Gurev, Pathmanathan, Fattebert, Wen, Magerlein, Gray, Richards and Rice2015). During this phase the atrial pressure is kept constant to the values reached when the mitral and tricuspid valves close.
$^{n+1}$
is as usual understood. Alternatively, a Lagrange multiplier approach could be employed (Gurev et al.
Reference Gurev, Pathmanathan, Fattebert, Wen, Magerlein, Gray, Richards and Rice2015). During this phase the atrial pressure is kept constant to the values reached when the mitral and tricuspid valves close.
For ventricular ejection, a reduced 0D model (based on the analogy with electrical circuits: see Section 4.5.1) for the systemic (or pulmonary) circulation is usually coupled with the cardiac mechanics problem, assuming that the ventricular pressure equals the pressure in the aorta (or in the pulmonary artery) (Usyk et al.
Reference Usyk, Legrice and Mcculloch2002, Eriksson et al.
Reference Eriksson, Prassl, Plank and Holzapfel2013). This is a good approximation since, although the ventricular and circulatory pressures are different (thus allowing for the acceleration and deceleration of blood: see Figure 5.2), they are very similar. In this case we have a coupled problem between the cardiac mechanics and the lumped parameter model where the two subproblems exchange suitable interface conditions (e.g. in an iterative framework). For example, the 0D model could provide the pressure to be prescribed to the mechanics problem by means of (7.32), whereas the flow rate
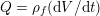 $Q=\unicode[STIX]{x1D70C}_{f}(\text{d}V/\text{d}t)$
is prescribed to the 0D model. During the ejection phase the atrial pressure is determined by the venous pressure, which could be obtained with a 0D model or by values from the literature.
$Q=\unicode[STIX]{x1D70C}_{f}(\text{d}V/\text{d}t)$
is prescribed to the 0D model. During the ejection phase the atrial pressure is determined by the venous pressure, which could be obtained with a 0D model or by values from the literature.
Finally, during isovolumic relaxation the endocardial pressure is decreased according to values from the literature until it reaches the pressure atrial value. Also during this phase the atrial pressure is determined by the venous pressure.
When only the ventricular mechanics is modelled (no atria), a truncated computational domain is considered, like the one depicted in Figure 7.2(a). In this case we have to provide suitable boundary conditions for the ventricular base
![]() $\unicode[STIX]{x1D6F4}_{b}$
. Often, this surface is kept fixed by enforcing homogeneous Dirichlet conditions. In other cases, the tangential displacement is allowed by prescribing a homogeneous Neumann condition along the tangential directions.
$\unicode[STIX]{x1D6F4}_{b}$
. Often, this surface is kept fixed by enforcing homogeneous Dirichlet conditions. In other cases, the tangential displacement is allowed by prescribing a homogeneous Neumann condition along the tangential directions.
7.2.4 Numerical approximation
The coupled electromechanical problem (7.31) is composed of four different blocks, namely the two PDEs (7.31a ) and (7.31c ) describing the heart mechanics and electrical propagation, respectively, the ODE system (7.31b ) providing the active stress function, and the ODE systems (7.31d ) modelling gating and ionic concentration variables. Moreover, the algebraic source of coupling (7.29, 7.30) needs to be accounted for to determine the stretch-activated ion currents. Their influence on the electrical problem has been included directly in the right-hand side of (7.31c ).
A common numerical solution strategy for problem (7.31) addresses the two PDEs (7.31a ) and (7.31c ) separately by relying (when possible) on pre-existing mechanics and electrical codes: for instance, the mechanics subproblem is solved by Pavarino et al. (Reference Pavarino, Scacchi and Zampini2015) using efficient Newton–Krylov iterations, while the electrical subproblem (monodomain+cell ODE model) is solved by means of one of the strategies described in Section 7.1.6 (see also Sundnes et al. Reference Sundnes, Wall, Osnes, Thorvaldsen and Mcculloch2014 for an operator splitting method).
In this context, at each time step the electrical subproblem is solved first and the mechanics problem later (Nash and Panfilov Reference Nash and Panfilov2004, Gurev et al.
Reference Gurev, Pathmanathan, Fattebert, Wen, Magerlein, Gray, Richards and Rice2015, Sundnes et al.
Reference Sundnes, Wall, Osnes, Thorvaldsen and Mcculloch2014). In particular, after time discretization, the following scheme is employed (as usual the current temporal index
![]() $^{n+1}$
is understood and
$^{n+1}$
is understood and
![]() $^{\ast }$
means that the related term could be treated either implicitly or explicitly, depending on the temporal scheme used).
$^{\ast }$
means that the related term could be treated either implicitly or explicitly, depending on the temporal scheme used).
Algorithm EM1
At each time step:
-
(1) Solve the monodomain problem together with the cell model:
(7.33a ) $$\begin{eqnarray}\displaystyle \displaystyle \widehat{V}_{m}={\mathcal{M}}(\widehat{V}_{m}^{\ast };\widehat{\boldsymbol{d}}^{n},\widehat{\boldsymbol{w}}^{\ast },\widehat{\boldsymbol{c}}^{\ast }) & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
(7.33b )
$$\begin{eqnarray}\displaystyle \displaystyle \widehat{V}_{m}={\mathcal{M}}(\widehat{V}_{m}^{\ast };\widehat{\boldsymbol{d}}^{n},\widehat{\boldsymbol{w}}^{\ast },\widehat{\boldsymbol{c}}^{\ast }) & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
(7.33b ) $$\begin{eqnarray}\displaystyle \displaystyle (\widehat{\boldsymbol{w}},\widehat{\boldsymbol{c}})={\mathcal{G}}(\widehat{\boldsymbol{w}}^{\ast },\widehat{\boldsymbol{c}}^{\ast };\widehat{V}_{m}^{\ast }) & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle (\widehat{\boldsymbol{w}},\widehat{\boldsymbol{c}})={\mathcal{G}}(\widehat{\boldsymbol{w}}^{\ast },\widehat{\boldsymbol{c}}^{\ast };\widehat{V}_{m}^{\ast }) & & \displaystyle \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}.\end{eqnarray}$$
-
(2) Then, solve the following mechanics problem.
-
(2a) Update the active stress contribution
 $$\begin{eqnarray}\widehat{\boldsymbol{T}}_{s}^{A}=P^{A}\boldsymbol{a}_{f}\otimes \widehat{\boldsymbol{a}}_{f},\quad P^{A}={\mathcal{A}}\biggl(\widehat{\boldsymbol{c}},\widehat{\boldsymbol{d}}^{n},\frac{\widehat{\boldsymbol{d}}^{n}-\widehat{\boldsymbol{d}}^{n-1}}{\unicode[STIX]{x1D6E5}t}\biggr)\quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}.\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\boldsymbol{T}}_{s}^{A}=P^{A}\boldsymbol{a}_{f}\otimes \widehat{\boldsymbol{a}}_{f},\quad P^{A}={\mathcal{A}}\biggl(\widehat{\boldsymbol{c}},\widehat{\boldsymbol{d}}^{n},\frac{\widehat{\boldsymbol{d}}^{n}-\widehat{\boldsymbol{d}}^{n-1}}{\unicode[STIX]{x1D6E5}t}\biggr)\quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}.\end{eqnarray}$$
-
(2b) Solve the equilibrium equation by means of the following Newton iterations. At each iteration
 $k$
solve
$k$
solve  $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FB}\cdot (D_{F}\widehat{\boldsymbol{T}}_{s}^{P}(\widehat{\boldsymbol{d}}_{(k-1)}))\unicode[STIX]{x1D6FF}\widehat{\boldsymbol{d}}_{(k)}\nonumber\\ \displaystyle & & \displaystyle \qquad =-\unicode[STIX]{x1D6FB}\cdot \biggl(\widehat{\boldsymbol{T}}_{s}^{P}(\widehat{\boldsymbol{d}}_{(k-1)})+\widehat{\boldsymbol{T}}_{s}^{A}\biggl(\widehat{\boldsymbol{c}},\widehat{\boldsymbol{d}}^{n},\frac{\widehat{\boldsymbol{d}}^{n}-\widehat{\boldsymbol{d}}^{n-1}}{\unicode[STIX]{x1D6E5}t}\biggr)\biggr)\quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FB}\cdot (D_{F}\widehat{\boldsymbol{T}}_{s}^{P}(\widehat{\boldsymbol{d}}_{(k-1)}))\unicode[STIX]{x1D6FF}\widehat{\boldsymbol{d}}_{(k)}\nonumber\\ \displaystyle & & \displaystyle \qquad =-\unicode[STIX]{x1D6FB}\cdot \biggl(\widehat{\boldsymbol{T}}_{s}^{P}(\widehat{\boldsymbol{d}}_{(k-1)})+\widehat{\boldsymbol{T}}_{s}^{A}\biggl(\widehat{\boldsymbol{c}},\widehat{\boldsymbol{d}}^{n},\frac{\widehat{\boldsymbol{d}}^{n}-\widehat{\boldsymbol{d}}^{n-1}}{\unicode[STIX]{x1D6E5}t}\biggr)\biggr)\quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}.\nonumber\end{eqnarray}$$
-
Using the notation introduced in Section 4.6.2,
![]() $D_{F}$
is the Gâteaux derivative with respect to
$D_{F}$
is the Gâteaux derivative with respect to
![]() $\boldsymbol{F}$
,
$\boldsymbol{F}$
,
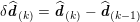 $\unicode[STIX]{x1D6FF}\widehat{\boldsymbol{d}}_{(k)}=\widehat{\boldsymbol{d}}_{(k)}-\widehat{\boldsymbol{d}}_{(k-1)}$
, and, for simplicity, we have considered a Forward Euler approximation of
$\unicode[STIX]{x1D6FF}\widehat{\boldsymbol{d}}_{(k)}=\widehat{\boldsymbol{d}}_{(k)}-\widehat{\boldsymbol{d}}_{(k-1)}$
, and, for simplicity, we have considered a Forward Euler approximation of
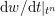 $\text{d}w/\text{d}t|_{t^{n}}$
. The active stress contribution is treated explicitly, that is, it is updated once per time step. This choice may lead to numerical instabilities, as reported computationally in Niederer and Smith (Reference Niederer and Smith2008). Pathmanathan et al. (Reference Pathmanathan, Chapman, Gavaghan and Whiteley2010) speculate that such instability could be ascribed to the (necessarily) explicit time discretization of the explicit stretch rate term
$\text{d}w/\text{d}t|_{t^{n}}$
. The active stress contribution is treated explicitly, that is, it is updated once per time step. This choice may lead to numerical instabilities, as reported computationally in Niederer and Smith (Reference Niederer and Smith2008). Pathmanathan et al. (Reference Pathmanathan, Chapman, Gavaghan and Whiteley2010) speculate that such instability could be ascribed to the (necessarily) explicit time discretization of the explicit stretch rate term
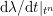 $\text{d}\unicode[STIX]{x1D706}/\text{d}t|_{t^{n}}$
(instead of
$\text{d}\unicode[STIX]{x1D706}/\text{d}t|_{t^{n}}$
(instead of
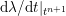 $\text{d}\unicode[STIX]{x1D706}/\text{d}t|_{t^{n+1}}$
) in the active stress function solution.
$\text{d}\unicode[STIX]{x1D706}/\text{d}t|_{t^{n+1}}$
) in the active stress function solution.
To overcome these instabilities, Niederer and Smith (Reference Niederer and Smith2008) propose updating the active stress function at each Newton step, that is, to replace step (2) in Algorithm EM1 with the following one.
Algorithm EM1
 $^{\prime }$
$^{\prime }$
-
(2’) Solve the mechanics problem by means of the following Newton iterations. At each iteration
 $k$
:
$k$
:-
(2’a) Update the active stress contribution:
 $$\begin{eqnarray}\widehat{\boldsymbol{T}}_{s}^{A}=P^{A}\boldsymbol{a}_{f}\otimes \widehat{\boldsymbol{a}}_{f},\quad P^{A}={\mathcal{A}}\biggl(\widehat{\boldsymbol{c}},\widehat{\boldsymbol{d}}_{(k-1)},\frac{\widehat{\boldsymbol{d}}_{(k-1)}-\widehat{\boldsymbol{d}}^{n}}{\unicode[STIX]{x1D6E5}t}\biggr)\quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}.\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\boldsymbol{T}}_{s}^{A}=P^{A}\boldsymbol{a}_{f}\otimes \widehat{\boldsymbol{a}}_{f},\quad P^{A}={\mathcal{A}}\biggl(\widehat{\boldsymbol{c}},\widehat{\boldsymbol{d}}_{(k-1)},\frac{\widehat{\boldsymbol{d}}_{(k-1)}-\widehat{\boldsymbol{d}}^{n}}{\unicode[STIX]{x1D6E5}t}\biggr)\quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}.\end{eqnarray}$$
-
(2’b) Solve the equilibrium equation:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FB}\cdot (D_{F}\widehat{\boldsymbol{T}}_{s}^{P}(\widehat{\boldsymbol{d}}_{k-1}))\unicode[STIX]{x1D6FF}\widehat{\boldsymbol{d}}_{k}\nonumber\\ \displaystyle & & \displaystyle \qquad =-\unicode[STIX]{x1D6FB}\cdot \biggl(\widehat{\boldsymbol{T}}_{s}^{P}(\widehat{\boldsymbol{d}}_{k-1})+\widehat{\boldsymbol{T}}_{s}^{A}\biggl(\widehat{\boldsymbol{c}},\widehat{\boldsymbol{d}}_{(k-1)},\frac{\widehat{\boldsymbol{d}}_{(k-1)}-\widehat{\boldsymbol{d}}^{n}}{\unicode[STIX]{x1D6E5}t}\biggr)\biggr)\quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FB}\cdot (D_{F}\widehat{\boldsymbol{T}}_{s}^{P}(\widehat{\boldsymbol{d}}_{k-1}))\unicode[STIX]{x1D6FF}\widehat{\boldsymbol{d}}_{k}\nonumber\\ \displaystyle & & \displaystyle \qquad =-\unicode[STIX]{x1D6FB}\cdot \biggl(\widehat{\boldsymbol{T}}_{s}^{P}(\widehat{\boldsymbol{d}}_{k-1})+\widehat{\boldsymbol{T}}_{s}^{A}\biggl(\widehat{\boldsymbol{c}},\widehat{\boldsymbol{d}}_{(k-1)},\frac{\widehat{\boldsymbol{d}}_{(k-1)}-\widehat{\boldsymbol{d}}^{n}}{\unicode[STIX]{x1D6E5}t}\biggr)\biggr)\quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}.\nonumber\end{eqnarray}$$
-
Note that step
![]() $(2^{\prime })$
does not coincide with a Newton iteration for (7.31a
, 7.31b
). Although at the expense of a higher number of iterations, this scheme provides stable solutions and allows the use of a standard solver for the mechanics part.
$(2^{\prime })$
does not coincide with a Newton iteration for (7.31a
, 7.31b
). Although at the expense of a higher number of iterations, this scheme provides stable solutions and allows the use of a standard solver for the mechanics part.
A Newton method for the solution of the mechanics problem (7.31a , 7.31b ), used in combination with a different explicit decoupled scheme, has been successfully proposed by Pavarino et al. (Reference Pavarino, Scacchi and Zampini2015), who split the electrical problem (7.31c , 7.31d ) into the cellular and macroscopic problems (semi-implicit treatment), and solved the mechanics problem in between, as follows.
Algorithm EM2
At each time step:
-
(1) Solve the ODE system for the gating and ionic concentration variables
 $$\begin{eqnarray}(\widehat{\boldsymbol{w}},\widehat{\boldsymbol{c}})={\mathcal{G}}(\widehat{\boldsymbol{w}}^{\ast },\widehat{\boldsymbol{c}}^{\ast };\widehat{V}_{m}^{\ast })\quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}.\end{eqnarray}$$
$$\begin{eqnarray}(\widehat{\boldsymbol{w}},\widehat{\boldsymbol{c}})={\mathcal{G}}(\widehat{\boldsymbol{w}}^{\ast },\widehat{\boldsymbol{c}}^{\ast };\widehat{V}_{m}^{\ast })\quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}.\end{eqnarray}$$
-
(2) Then, solve the mechanics problem by means of the following Newton method. At each iteration
 $k$
solve:
$k$
solve:-
(2a) Update the active stress contribution:
 $$\begin{eqnarray}\widehat{\boldsymbol{T}}_{s}^{A}=P^{A}\boldsymbol{a}_{f}\otimes \widehat{\boldsymbol{a}}_{f},\quad P^{A}={\mathcal{A}}\biggl(\widehat{\boldsymbol{c}},\widehat{\boldsymbol{d}}_{(k-1)},\frac{\widehat{\boldsymbol{d}}_{(k-1)}-\widehat{\boldsymbol{d}}^{n}}{\unicode[STIX]{x1D6E5}t}\biggr)\quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}.\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\boldsymbol{T}}_{s}^{A}=P^{A}\boldsymbol{a}_{f}\otimes \widehat{\boldsymbol{a}}_{f},\quad P^{A}={\mathcal{A}}\biggl(\widehat{\boldsymbol{c}},\widehat{\boldsymbol{d}}_{(k-1)},\frac{\widehat{\boldsymbol{d}}_{(k-1)}-\widehat{\boldsymbol{d}}^{n}}{\unicode[STIX]{x1D6E5}t}\biggr)\quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}.\end{eqnarray}$$
-
(2b) Solve the equilibrium equation:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FB}\cdot \biggl(D_{F}\widehat{\boldsymbol{T}}_{s}^{P}(\widehat{\boldsymbol{d}}_{(k-1)})+D_{F}\widehat{\boldsymbol{T}}_{s}^{A}\biggl(\widehat{\boldsymbol{c}},\widehat{\boldsymbol{d}}_{(k-1)},\frac{\widehat{\boldsymbol{d}}_{(k-1)}-\widehat{\boldsymbol{d}}^{n}}{\unicode[STIX]{x1D6E5}t}\biggr)\biggr)\unicode[STIX]{x1D6FF}\widehat{\boldsymbol{d}}_{(k)}\nonumber\\ \displaystyle & & \displaystyle \qquad =-\unicode[STIX]{x1D6FB}\cdot \biggl(\widehat{\boldsymbol{T}}_{s}^{P}(\widehat{\boldsymbol{d}}_{(k-1)})+\widehat{\boldsymbol{T}}_{s}^{A}\biggl(\widehat{\boldsymbol{c}},\widehat{\boldsymbol{d}}_{(k-1)},\frac{\widehat{\boldsymbol{d}}_{(k-1)}-\widehat{\boldsymbol{d}}^{n}}{\unicode[STIX]{x1D6E5}t}\biggr)\biggr)\quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FB}\cdot \biggl(D_{F}\widehat{\boldsymbol{T}}_{s}^{P}(\widehat{\boldsymbol{d}}_{(k-1)})+D_{F}\widehat{\boldsymbol{T}}_{s}^{A}\biggl(\widehat{\boldsymbol{c}},\widehat{\boldsymbol{d}}_{(k-1)},\frac{\widehat{\boldsymbol{d}}_{(k-1)}-\widehat{\boldsymbol{d}}^{n}}{\unicode[STIX]{x1D6E5}t}\biggr)\biggr)\unicode[STIX]{x1D6FF}\widehat{\boldsymbol{d}}_{(k)}\nonumber\\ \displaystyle & & \displaystyle \qquad =-\unicode[STIX]{x1D6FB}\cdot \biggl(\widehat{\boldsymbol{T}}_{s}^{P}(\widehat{\boldsymbol{d}}_{(k-1)})+\widehat{\boldsymbol{T}}_{s}^{A}\biggl(\widehat{\boldsymbol{c}},\widehat{\boldsymbol{d}}_{(k-1)},\frac{\widehat{\boldsymbol{d}}_{(k-1)}-\widehat{\boldsymbol{d}}^{n}}{\unicode[STIX]{x1D6E5}t}\biggr)\biggr)\quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}.\nonumber\end{eqnarray}$$
-
-
(3) Solve the monodomain problem:
 $$\begin{eqnarray}\widehat{V}_{m}={\mathcal{M}}(\widehat{V}_{m}^{\ast };\widehat{\boldsymbol{d}},\widehat{\boldsymbol{w}},\widehat{\boldsymbol{c}})\quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}.\end{eqnarray}$$
$$\begin{eqnarray}\widehat{V}_{m}={\mathcal{M}}(\widehat{V}_{m}^{\ast };\widehat{\boldsymbol{d}},\widehat{\boldsymbol{w}},\widehat{\boldsymbol{c}})\quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}.\end{eqnarray}$$
Andreianov et al. (Reference Andreianov, Bendahmane, Quarteroni and Ruiz-Baier2015) have proposed a simplified variant of the above decoupled algorithms for the active strain formulation.Footnote
2
We provide the same variant below for the active stress formulation; in the second equation of (7.31b
), however, the active stress function
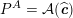 $P^{A}={\mathcal{A}}(\widehat{\boldsymbol{c}})$
does not depend on the stretch and stretch rate.
$P^{A}={\mathcal{A}}(\widehat{\boldsymbol{c}})$
does not depend on the stretch and stretch rate.
Algorithm EM3
At each time step:
-
(1) Update the active stress contribution:
 $$\begin{eqnarray}\widehat{\boldsymbol{T}}_{s}^{A}=P^{A}\boldsymbol{a}_{f}\otimes \widehat{\boldsymbol{a}}_{f},\quad P^{A}={\mathcal{A}}(\widehat{\boldsymbol{c}}^{n-1})\quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}.\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\boldsymbol{T}}_{s}^{A}=P^{A}\boldsymbol{a}_{f}\otimes \widehat{\boldsymbol{a}}_{f},\quad P^{A}={\mathcal{A}}(\widehat{\boldsymbol{c}}^{n-1})\quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}.\end{eqnarray}$$
-
(2) Solve the equilibrium mechanics problem via the following Newton method. At each iteration
 $k$
solve
$k$
solve  $$\begin{eqnarray}\unicode[STIX]{x1D6FB}\cdot (D_{F}\widehat{\boldsymbol{T}}_{s}^{P}(\widehat{\boldsymbol{d}}_{k-1}))\unicode[STIX]{x1D6FF}\widehat{\boldsymbol{d}}_{k}=-\unicode[STIX]{x1D6FB}\cdot (\widehat{\boldsymbol{T}}_{s}^{P}(\widehat{\boldsymbol{d}}_{k-1})+\widehat{\boldsymbol{T}}_{s}^{A}(\widehat{\boldsymbol{c}}^{n-1}))\quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FB}\cdot (D_{F}\widehat{\boldsymbol{T}}_{s}^{P}(\widehat{\boldsymbol{d}}_{k-1}))\unicode[STIX]{x1D6FF}\widehat{\boldsymbol{d}}_{k}=-\unicode[STIX]{x1D6FB}\cdot (\widehat{\boldsymbol{T}}_{s}^{P}(\widehat{\boldsymbol{d}}_{k-1})+\widehat{\boldsymbol{T}}_{s}^{A}(\widehat{\boldsymbol{c}}^{n-1}))\quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}.\end{eqnarray}$$
-
(3) Then, solve the electrical problem:
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}ll@{}}\displaystyle \widehat{V}_{m}={\mathcal{M}}(\widehat{V}_{m}^{\ast };\widehat{\boldsymbol{d}}^{n-1},\widehat{\boldsymbol{w}}^{\ast },\widehat{\boldsymbol{c}}^{\ast }) & \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\\ \displaystyle (\widehat{\boldsymbol{w}},\widehat{\boldsymbol{c}})={\mathcal{G}}(\widehat{\boldsymbol{w}}^{\ast },\widehat{\boldsymbol{c}}^{\ast };\widehat{V}_{m}^{\ast }) & \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}.\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}ll@{}}\displaystyle \widehat{V}_{m}={\mathcal{M}}(\widehat{V}_{m}^{\ast };\widehat{\boldsymbol{d}}^{n-1},\widehat{\boldsymbol{w}}^{\ast },\widehat{\boldsymbol{c}}^{\ast }) & \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\\ \displaystyle (\widehat{\boldsymbol{w}},\widehat{\boldsymbol{c}})={\mathcal{G}}(\widehat{\boldsymbol{w}}^{\ast },\widehat{\boldsymbol{c}}^{\ast };\widehat{V}_{m}^{\ast }) & \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}.\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
Although segregated algorithms such as those reported above are the most widely used for numerical solution of the coupled electromechanics problem (7.31), a monolithic approach has been used by Goktepe and Kuhl (Reference Goktepe and Kuhl2010), who have successfully applied a Newton method to the whole coupled problem with a FitzHugh–Nagumo cardiac cell model (i.e. without the ODE systems (7.31d )).
In Figure 7.5 we show an example of fibre configuration in the left ventricle, and in the same figure and Figure 7.6 we give the results of an electromechanical simulation.

Figure 7.5. (a) Fibre orientation in a real left ventricle obtained with the method proposed in Rossi et al. (Reference Rossi, Lassila, Ruiz-Baier, Sequeira and Quarteroni2014). CT images from the Cardiology Division of Ospedale S. Maria del Carmine, Rovereto (TN), Italy, and from the Radiology Division of Borgo-Trento (TN), Italy. (b) Displacement configuration of a real left ventricle during the contraction phase at three different times. Orthotropic model of activation: see Barbarotta (Reference Barbarotta2014). Numerical results were obtained using LifeV and taken from Barbarotta (Reference Barbarotta2014); CT images from the Cardio Surgery and Radiology Divisions at Ospedale Sacco, Milan, Italy.

Figure 7.6. Displacements of the two ventricles at six different times during systolic contraction. Electromechanical coupled simulation, P1 finite elements. Numerical results were obtained using LifeV; the computational mesh was obtained from an open source biventricular geometry segmented from CT images: see Rousseau (Reference Rousseau2010).
7.3 The ventricular fluid dynamics
Blood flow in heart cavities
![]() $\unicode[STIX]{x1D6FA}_{\mathit{cav}}$
, shown in Figure 6.1, can be regarded as homogeneous, Newtonian and incompressible (Vierendeels et al.
Reference Vierendeels, Riemslagh, Dick and Verdonck2000, Watanabe et al.
Reference Watanabe, Hisada, Sugiura, Okada and Fukunari2002). The displacements induced by the interaction with the myocardium can be larger than 30%, so the solution of fluid–structure interaction problems is mandatory. Despite the large displacements, the ALE technique introduced in Section 4.6.3 is suitable in this context, as shown by several authors: see e.g. Cheng, Oertel and Schenkel (Reference Cheng, Oertel and Schenkel2005) and Nordsletten et al. (Reference Nordsletten, Mccormick, Kilner, Hunter, Kayand and Smith2011a
). Alternatively, the immersed boundary method (Peskin Reference Peskin1972), which does not require remeshing or induced mesh deformation, has often been used since the celebrated paper by Peskin (Mittal et al. Reference Mittal, Seo, Vedula, Choi, Liu, Huang, Jain, Younes, Abraham and George2016, Choi et al. Reference Choi, Constantino, Vedula, Trayanova and Mittal2015); see Section 7.4 for a mathematical description.
$\unicode[STIX]{x1D6FA}_{\mathit{cav}}$
, shown in Figure 6.1, can be regarded as homogeneous, Newtonian and incompressible (Vierendeels et al.
Reference Vierendeels, Riemslagh, Dick and Verdonck2000, Watanabe et al.
Reference Watanabe, Hisada, Sugiura, Okada and Fukunari2002). The displacements induced by the interaction with the myocardium can be larger than 30%, so the solution of fluid–structure interaction problems is mandatory. Despite the large displacements, the ALE technique introduced in Section 4.6.3 is suitable in this context, as shown by several authors: see e.g. Cheng, Oertel and Schenkel (Reference Cheng, Oertel and Schenkel2005) and Nordsletten et al. (Reference Nordsletten, Mccormick, Kilner, Hunter, Kayand and Smith2011a
). Alternatively, the immersed boundary method (Peskin Reference Peskin1972), which does not require remeshing or induced mesh deformation, has often been used since the celebrated paper by Peskin (Mittal et al. Reference Mittal, Seo, Vedula, Choi, Liu, Huang, Jain, Younes, Abraham and George2016, Choi et al. Reference Choi, Constantino, Vedula, Trayanova and Mittal2015); see Section 7.4 for a mathematical description.
One of the main features of the intraventricular fluid dynamics is represented by the formation of a vortex ring during diastole (i.e. the filling phase) just downstream of the mitral valve. This ring is generated during the peak flow due to a pressure gradient between left atrium and ventricle, and it is highly distorted due to the asymmetry of the mitral valve leaflets (Seo et al.
Reference Seo, Vedula, Abraham, Lardo, Dawoud, Luo and Mittal2014). At the end of this phase, the vortex ring is broken up into small-scale structures that propagate towards the posterior wall and the apex. After the second mitral peak flow due to the atrium contraction, additional vortex rings pop up. However, due to the small duration of this phase, they do not propagate far into the chamber (Le and Sotiropoulos Reference Le and Sotiropoulos2013). Similar vortex rings are generated in the left atrium from the flow ejected by the pulmonary vein (Mittal et al.
Reference Mittal, Seo, Vedula, Choi, Liu, Huang, Jain, Younes, Abraham and George2016). This complex and disturbed fluid dynamics, in the presence of a fairly high Reynolds number (
![]() $\simeq 4000$
), leads to transition to turbulence effects even in healthy cases (Querzoli, Fortini and Cenedese Reference Querzoli, Fortini and Cenedese2010). For this reason, it is common practice to include a suitable turbulence model in heart simulations; see e.g. Chnafa, Mendez and Nicoud (Reference Chnafa, Mendez and Nicoud2014) for LES models and Tagliabue, Dede’ and Quarteroni (Reference Tagliabue, Dede’ and Quarteroni2015) for the variational multiscale (VMS) formulation.
$\simeq 4000$
), leads to transition to turbulence effects even in healthy cases (Querzoli, Fortini and Cenedese Reference Querzoli, Fortini and Cenedese2010). For this reason, it is common practice to include a suitable turbulence model in heart simulations; see e.g. Chnafa, Mendez and Nicoud (Reference Chnafa, Mendez and Nicoud2014) for LES models and Tagliabue, Dede’ and Quarteroni (Reference Tagliabue, Dede’ and Quarteroni2015) for the variational multiscale (VMS) formulation.
Regarding boundary conditions, on the endocardium
![]() $\unicode[STIX]{x1D6F4}_{\mathit{endo}}$
(Figure 6.1) the kinematic and dynamic conditions are implicitly determined by the coupling with the structural problem holding in the myocardium, leading to a fluid–structure interaction problem (see Section 7.5). The solution of a coupled fluid–structure interaction (FSI) problem can be avoided in those cases where the wall velocity can be derived from dynamic MRI or CT images. However, this requires us to have at our disposal several (20–30) wall displacement fields at different time instants during every heartbeat. The wall myocardium velocity (which provides the Dirichlet boundary condition for the fluid equations in the ventricle) can be generated by numerically differentiating the displacement field (Khalafvand et al.
Reference Khalafvand, Zhong and Ng2014, Mittal et al.
Reference Mittal, Seo, Vedula, Choi, Liu, Huang, Jain, Younes, Abraham and George2016). Alternatively, the wall myocardium velocity could be provided by the solution of the electromechanics model if the latter were segregated from the fluid model (Choi et al.
Reference Choi, Constantino, Vedula, Trayanova and Mittal2015).
$\unicode[STIX]{x1D6F4}_{\mathit{endo}}$
(Figure 6.1) the kinematic and dynamic conditions are implicitly determined by the coupling with the structural problem holding in the myocardium, leading to a fluid–structure interaction problem (see Section 7.5). The solution of a coupled fluid–structure interaction (FSI) problem can be avoided in those cases where the wall velocity can be derived from dynamic MRI or CT images. However, this requires us to have at our disposal several (20–30) wall displacement fields at different time instants during every heartbeat. The wall myocardium velocity (which provides the Dirichlet boundary condition for the fluid equations in the ventricle) can be generated by numerically differentiating the displacement field (Khalafvand et al.
Reference Khalafvand, Zhong and Ng2014, Mittal et al.
Reference Mittal, Seo, Vedula, Choi, Liu, Huang, Jain, Younes, Abraham and George2016). Alternatively, the wall myocardium velocity could be provided by the solution of the electromechanics model if the latter were segregated from the fluid model (Choi et al.
Reference Choi, Constantino, Vedula, Trayanova and Mittal2015).
The heart also has four (virtual) sections that delimit it from the circulatory system, namely the aortic and pulmonary valve orifices (outlets) and the interfaces with the venae cavae and the pulmonary vein (inlets). In these cases, suitable conditions could be obtained by coupling the heart fluid dynamics with the aorta, the pulmonary artery, and the above-mentioned veins. These can be modelled by means of 3D, 1D or 0D models.
In the case of simulation in the left ventricle alone (see Figure 7.2(b)) we have to prescribe suitable boundary conditions at the mitral valve orifice
![]() $\unicode[STIX]{x1D6E4}_{\mathit{mitr}}$
as well. For example, Khalafvand et al. (Reference Khalafvand, Zhong and Ng2014) propose prescribing the flow rates at
$\unicode[STIX]{x1D6E4}_{\mathit{mitr}}$
as well. For example, Khalafvand et al. (Reference Khalafvand, Zhong and Ng2014) propose prescribing the flow rates at
![]() $\unicode[STIX]{x1D6E4}_{\mathit{mitr}}$
and at the aortic valve outlet
$\unicode[STIX]{x1D6E4}_{\mathit{mitr}}$
and at the aortic valve outlet
![]() $\unicode[STIX]{x1D6E4}_{ao}$
obtained by MRI measurements of the volume changes of the left ventricle chamber, noticing that the two valves are never open simultaneously. Alternatively, flow rate curves taken from the literature could be applied: see e.g. Nordsletten et al. (Reference Nordsletten, Mccormick, Kilner, Hunter, Kayand and Smith2011a
).
$\unicode[STIX]{x1D6E4}_{ao}$
obtained by MRI measurements of the volume changes of the left ventricle chamber, noticing that the two valves are never open simultaneously. Alternatively, flow rate curves taken from the literature could be applied: see e.g. Nordsletten et al. (Reference Nordsletten, Mccormick, Kilner, Hunter, Kayand and Smith2011a
).
7.4 Modelling the valves
Heart valves are made of thin leaflets. They do not cause any resistance to the blood during systole, and sustain large pressure gradients during diastole. Moreover, unlike the vascular vessel wall, they are subjected to very large displacements. Because of these features, the mathematical and numerical modelling of the valve mechanics and their interaction with blood flow is very demanding, requiring ad hoc techniques for their description. Our main focus will be on the aortic and mitral valves of the left ventricle, the most studied from the mathematical point of view. For recent reviews on valve modelling, see Marom (Reference Marom2015) and Votta et al. (Reference Votta, Le, Stevanella, Fusinic, Caiani, Redaelli and Sotiropoulos2013), for example.
7.4.1 Mechanical models of the leaflets
Due to fibre alignment, which occurs mostly in the circumferential direction
![]() $\boldsymbol{a}$
, and to the presence of collagen, most of the valve mechanical models proposed so far are of the non-linear transversally isotropic type. In particular, they depend on the two invariants
$\boldsymbol{a}$
, and to the presence of collagen, most of the valve mechanical models proposed so far are of the non-linear transversally isotropic type. In particular, they depend on the two invariants
 $I_{1}=\operatorname{tr}\boldsymbol{C}$
and
$I_{1}=\operatorname{tr}\boldsymbol{C}$
and
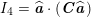 $I_{4}=\widehat{\boldsymbol{a}}\cdot (\boldsymbol{C}\widehat{\boldsymbol{a}})$
. For example, May-Newman, Lam and Yin (Reference May-Newman, Lam and Yin2009) and Prot, Skallerud and Holzapfel (Reference Prot, Skallerud and Holzapfel2007) use the strain energy function
$I_{4}=\widehat{\boldsymbol{a}}\cdot (\boldsymbol{C}\widehat{\boldsymbol{a}})$
. For example, May-Newman, Lam and Yin (Reference May-Newman, Lam and Yin2009) and Prot, Skallerud and Holzapfel (Reference Prot, Skallerud and Holzapfel2007) use the strain energy function
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}(I_{1},I_{4})=c[\text{e}^{b_{1}(I_{1}-3)^{2}+b_{4}(I_{4}-1)^{2}}-1],\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}(I_{1},I_{4})=c[\text{e}^{b_{1}(I_{1}-3)^{2}+b_{4}(I_{4}-1)^{2}}-1],\end{eqnarray}$$
for suitable constants
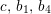 $c,\,b_{1},\,b_{4}$
. Variants of the above energy have been considered, for example by Humphrey and Yin (Reference Humphrey and Yin1987), May-Newman and Yin (Reference May-Newman and Yin1998) and Weinberg and Kaazempur-Mofrad (Reference Weinberg and Kaazempur-Mofrad2006). For a comparison of numerical results obtained with these constitutive laws, see Auricchio, Ferrara and Morganti (Reference Auricchio, Ferrara and Morganti2012). More sophisticated energy functions include the microstructure of the leaflet tissue: see e.g. Einstein et al. (Reference Einstein, Kunzelman, Reinhall, Nicosia and Cochran2005).
$c,\,b_{1},\,b_{4}$
. Variants of the above energy have been considered, for example by Humphrey and Yin (Reference Humphrey and Yin1987), May-Newman and Yin (Reference May-Newman and Yin1998) and Weinberg and Kaazempur-Mofrad (Reference Weinberg and Kaazempur-Mofrad2006). For a comparison of numerical results obtained with these constitutive laws, see Auricchio, Ferrara and Morganti (Reference Auricchio, Ferrara and Morganti2012). More sophisticated energy functions include the microstructure of the leaflet tissue: see e.g. Einstein et al. (Reference Einstein, Kunzelman, Reinhall, Nicosia and Cochran2005).
Due to their thinness, heart valves are often modelled as membrane shells by neglecting the shear bending forces, which are an order of magnitude smaller than the in-plane stresses (Merryman et al. Reference Merryman, Huang, Schoen and Sacks2006, Kim et al. Reference Kim, Lu, Sacks and Chandran2008, Hsu et al. Reference Hsu, Kamensky, Bazilevs, Sacks and Hughes2014).
Some works on the mitral valve also consider the presence of the chordae tendinae (see Section 5.1). These comprise independent ring models, where the chordae are modelled as non-linear springs with zero elasticity during compression and exponential-like stiffness during traction (Kunzelman and Cochran Reference Kunzelman and Cochran1990, Mansi et al. Reference Mansi, Voigt, Georgescu, Zheng, Mengue, Hackl, Ionasec, Noack, Seeburger and Comaniciu2012), and one-dimensional models characterized by a non-linear energy function (Einstein et al. Reference Einstein, Kunzelman, Reinhall, Nicosia and Cochran2005, Votta et al. Reference Votta, Maisano, Bolling, Alfieri, Montevecchi and Redaelli2007, Padala et al. Reference Padala, Sacks, Liou, Balachandran, He and Yoganathan2010).
Another difficulty arises when modelling the contact among the leaflets during closure. A common strategy to handle this process is a penalty method (Hsu et al. Reference Hsu, Kamensky, Bazilevs, Sacks and Hughes2014, Marom Reference Marom2015, Mansi et al. Reference Mansi, Voigt, Georgescu, Zheng, Mengue, Hackl, Ionasec, Noack, Seeburger and Comaniciu2012). This is based on measuring the distance between each vertex and the closest leaflet, and on locating a spring between the vertex and the collision point when the distance is below a critical value. Astorino et al. (Reference Astorino, Gerbeau, Pantz and Traoré2010) propose a more sophisticated algorithm, based on the introduction of sub-iterations that guarantee the satisfaction of the contact constraint via the introduction of Lagrange multipliers that act as a force of repulsion between the leaflets.
The numerical simulation of valve mechanics has usually been obtained by prescribing a pressure difference between the two sides of the leaflets, mimicking the effect of the fluid (Gnyaneshwar, Kumar and Balakrishnan Reference Gnyaneshwar, Kumar and Balakrishnan2002, Votta et al. Reference Votta, Le, Stevanella, Fusinic, Caiani, Redaelli and Sotiropoulos2013). However, more realistic models are obtained by considering the FSI problem arising between the blood flow and the leaflets. This is the topic of the next two subsections.
7.4.2 Reduced models for fluid–valve interaction
As noticed, the simulation of the fluid–structure interaction between blood and valve leaflets is computationally demanding. However, if one is interested only in the fluid-dynamic quantities and not in the internal leaflet stresses, reduced models could be considered.
The first family does not explicitly represent the leaflets; rather, only the opening/closure mechanism of the valve is modelled through the description of the valve orifice. The simplest strategy consists in a priori operating the opening and closing of the valve on the basis of a flow rate or pressure profile obtained from the literature or from clinical data: see e.g. Faggiano et al. (Reference Faggiano, Antiga, Puppini, Quarteroni, Luciani and Vergara2013). For an example, see Bazilevs et al. (Reference Bazilevs, Gohean, Hughes, Moser and Zhang2009), Vergara et al. (Reference Vergara, Viscardi, Antiga and Luciani2012) and Nestola et al. (Reference Nestola, Faggiano, Vergara, Lancellotti, Ippolito, Antona, Quarteroni and Scrofani2017) for the flow simulation in the aorta and Khalafvand et al. (Reference Khalafvand, Zhong and Ng2014) for that in the left ventricle. A more realistic situation is obtained by simulating the opening/closure mechanism of the aortic valve orifice by means of the following conditions prescribed to the fluid problem:
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}ll@{}}\text{if }P_{u}>P_{d} & \text{then the valve opens},\\ \text{if }Q_{d}<0 & \text{then the valve closes},\end{array} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}ll@{}}\text{if }P_{u}>P_{d} & \text{then the valve opens},\\ \text{if }Q_{d}<0 & \text{then the valve closes},\end{array} & & \displaystyle\end{eqnarray}$$
where
![]() $P_{u}$
is the upstream pressure and
$P_{u}$
is the upstream pressure and
![]() $P_{d}$
and
$P_{d}$
and
![]() $Q_{d}$
are the downstream pressure and flow rate (Formaggia et al.
Reference Formaggia, Nobile, Quarteroni and Veneziani1999). The quantities
$Q_{d}$
are the downstream pressure and flow rate (Formaggia et al.
Reference Formaggia, Nobile, Quarteroni and Veneziani1999). The quantities
 $P_{u},P_{d},Q_{d}$
could be prescribed as data or else be the results of the numerical computation of the flow field. For example, in a fluid-dynamic simulation in the aorta,
$P_{u},P_{d},Q_{d}$
could be prescribed as data or else be the results of the numerical computation of the flow field. For example, in a fluid-dynamic simulation in the aorta,
![]() $P_{u}$
is the prescribed left ventricular pressure, and
$P_{u}$
is the prescribed left ventricular pressure, and
![]() $P_{d}$
and
$P_{d}$
and
![]() $Q_{d}$
are the unknown aortic pressure and flow rate. For a left ventricular flow simulation, the situation is more involved as we have to distinguish between the mitral and the aortic valve: for the former,
$Q_{d}$
are the unknown aortic pressure and flow rate. For a left ventricular flow simulation, the situation is more involved as we have to distinguish between the mitral and the aortic valve: for the former,
![]() $P_{u}$
is the prescribed atrial pressure and
$P_{u}$
is the prescribed atrial pressure and
![]() $P_{d}$
and
$P_{d}$
and
![]() $Q_{d}$
are the unknown left ventricular pressure and flow rate; for the latter,
$Q_{d}$
are the unknown left ventricular pressure and flow rate; for the latter,
![]() $P_{u}$
is the unknown left ventricular pressure, and
$P_{u}$
is the unknown left ventricular pressure, and
![]() $P_{d}$
and
$P_{d}$
and
![]() $Q_{d}$
the prescribed aortic pressure and flow rate. Many works have considered a zero-dimensional model of the systemic circulation to provide the latter quantities (Wenk et al.
Reference Wenk, Ge, Zhang, Soleimani, Potter, Wallace, Tseng, Ratcliffe and Guccione2013). In any case, the opening/closure mechanism is not prescribed a priori. This leads to a non-linear boundary condition for the fluid problem at the valve orifice which, in the electric circuit analogy of zero-dimensional models (see Section 4.5.1), is represented by an ideal diode. Similar models have been proposed by Korakianitis and Shi (Reference Korakianitis and Shi2006b
) and Blanco and Feijóo (Reference Blanco and Feijóo2013), to account for diseased valves, by introducing a suitable non-ideal law for the diode. More refined reduced models consider the opening/closure mechanism not simply in an on–off mode: the open part of the orifice dynamically changes continuously by projecting the supposed leaflet position on the orifice plane. For example, in Sundaram, Balakrishnan and Kumar (Reference Sundaram, Balakrishnan and Kumar2015) the dynamics of the valve orifice opening/closure is given by a prescribed law, whereas in Korakianitis and Shi (Reference Korakianitis and Shi2006a
) it is given by
$Q_{d}$
the prescribed aortic pressure and flow rate. Many works have considered a zero-dimensional model of the systemic circulation to provide the latter quantities (Wenk et al.
Reference Wenk, Ge, Zhang, Soleimani, Potter, Wallace, Tseng, Ratcliffe and Guccione2013). In any case, the opening/closure mechanism is not prescribed a priori. This leads to a non-linear boundary condition for the fluid problem at the valve orifice which, in the electric circuit analogy of zero-dimensional models (see Section 4.5.1), is represented by an ideal diode. Similar models have been proposed by Korakianitis and Shi (Reference Korakianitis and Shi2006b
) and Blanco and Feijóo (Reference Blanco and Feijóo2013), to account for diseased valves, by introducing a suitable non-ideal law for the diode. More refined reduced models consider the opening/closure mechanism not simply in an on–off mode: the open part of the orifice dynamically changes continuously by projecting the supposed leaflet position on the orifice plane. For example, in Sundaram, Balakrishnan and Kumar (Reference Sundaram, Balakrishnan and Kumar2015) the dynamics of the valve orifice opening/closure is given by a prescribed law, whereas in Korakianitis and Shi (Reference Korakianitis and Shi2006a
) it is given by
 $$\begin{eqnarray}A_{V}=\frac{(1-\cos \unicode[STIX]{x1D703})^{2}}{(1-\cos \unicode[STIX]{x1D703}_{\max })^{2}},\end{eqnarray}$$
$$\begin{eqnarray}A_{V}=\frac{(1-\cos \unicode[STIX]{x1D703})^{2}}{(1-\cos \unicode[STIX]{x1D703}_{\max })^{2}},\end{eqnarray}$$
where
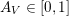 $A_{V}\in [0,1]$
is the percentage of open orifice area,
$A_{V}\in [0,1]$
is the percentage of open orifice area,
![]() $\unicode[STIX]{x1D703}$
is the opening leaflet angle (
$\unicode[STIX]{x1D703}$
is the opening leaflet angle (
![]() $\unicode[STIX]{x1D703}=0$
means closed valve) and
$\unicode[STIX]{x1D703}=0$
means closed valve) and
![]() $\unicode[STIX]{x1D703}_{\max }$
is the maximum opening angle. The value of
$\unicode[STIX]{x1D703}_{\max }$
is the maximum opening angle. The value of
![]() $\unicode[STIX]{x1D703}$
is determined by the ODE
$\unicode[STIX]{x1D703}$
is determined by the ODE
 $$\begin{eqnarray}\frac{\text{d}^{2}\unicode[STIX]{x1D703}}{\text{d}t^{2}}+k_{1}\frac{\text{d}\unicode[STIX]{x1D703}}{\text{d}t}+k_{2}(P_{d}-P_{u})\cos \unicode[STIX]{x1D703}=0,\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}^{2}\unicode[STIX]{x1D703}}{\text{d}t^{2}}+k_{1}\frac{\text{d}\unicode[STIX]{x1D703}}{\text{d}t}+k_{2}(P_{d}-P_{u})\cos \unicode[STIX]{x1D703}=0,\end{eqnarray}$$
for suitable parameters
![]() $k_{1}$
and
$k_{1}$
and
![]() $k_{2}$
and appropriate initial conditions on
$k_{2}$
and appropriate initial conditions on
![]() $\unicode[STIX]{x1D703}$
and
$\unicode[STIX]{x1D703}$
and
![]() $\text{d}\unicode[STIX]{x1D703}/\text{d}t$
.
$\text{d}\unicode[STIX]{x1D703}/\text{d}t$
.
For all these models, which do not explicitly include the leaflets, there might be a need to switch between Dirichlet and Neumann boundary conditions (and
vice versa
) along a single heartbeat in a fluid problem. Indeed, a Dirichlet condition is usually prescribed when the valve is closed (e.g. homogeneous in the physiological case), whereas a Neumann or a resistance condition might be preferred when the valve is open. This might be problematic at the numerical level, particularly in view of the implementation. Tagliabue, Dede’ and Quarteroni (Reference Tagliabue, Dede’ and Quarteroni2015) propose a new way to overcome this problem, based on a Robin-like condition implemented by means of the extended Nitsche’s method proposed in Juntunen and Stenberg (Reference Juntunen and Stenberg2009). For simplicity we detail the case of a Neumann-like condition for the open valve, and we refer the reader to Tagliabue et al. (Reference Tagliabue, Dede’ and Quarteroni2015) for the more physiological case of a resistance condition. Let
![]() $\unicode[STIX]{x1D6E4}$
be the valve orifice at hand, and suppose that one wants to prescribe at each time the following conditions:
$\unicode[STIX]{x1D6E4}$
be the valve orifice at hand, and suppose that one wants to prescribe at each time the following conditions:
 $$\begin{eqnarray}\displaystyle & \boldsymbol{u}=\boldsymbol{g}\quad \text{if the valve is closed}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \boldsymbol{u}=\boldsymbol{g}\quad \text{if the valve is closed}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \boldsymbol{T}_{f}\boldsymbol{n}=\boldsymbol{h}\quad \text{if the valve is open}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \boldsymbol{T}_{f}\boldsymbol{n}=\boldsymbol{h}\quad \text{if the valve is open}. & \displaystyle\end{eqnarray}$$
 $\boldsymbol{h}=P\boldsymbol{n}$
, where
$\boldsymbol{h}=P\boldsymbol{n}$
, where
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle -\int _{\unicode[STIX]{x1D6E4}}\frac{\unicode[STIX]{x1D6FE}h}{\unicode[STIX]{x1D709}+\unicode[STIX]{x1D6FE}h}\boldsymbol{T}_{f}(\boldsymbol{v},p)\boldsymbol{n}\cdot \boldsymbol{w}\text{d}\unicode[STIX]{x1D714}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad -\int _{\unicode[STIX]{x1D6E4}}\frac{\unicode[STIX]{x1D6FE}h}{\unicode[STIX]{x1D709}+\unicode[STIX]{x1D6FE}h}(\boldsymbol{v}-\boldsymbol{g})\cdot (\boldsymbol{T}_{f}(\boldsymbol{w},q)\boldsymbol{n})\text{d}\unicode[STIX]{x1D714}+\int _{\unicode[STIX]{x1D6E4}}\frac{1}{\unicode[STIX]{x1D709}+\unicode[STIX]{x1D6FE}h}(\boldsymbol{v}-\boldsymbol{g})\cdot \boldsymbol{w}\text{d}\unicode[STIX]{x1D714}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad -\int _{\unicode[STIX]{x1D6E4}}\frac{\unicode[STIX]{x1D709}\unicode[STIX]{x1D6FE}h}{\unicode[STIX]{x1D709}+\unicode[STIX]{x1D6FE}h}(\boldsymbol{T}_{f}(\boldsymbol{v},p)\boldsymbol{n}-\boldsymbol{h})\cdot (\boldsymbol{T}_{f}(\boldsymbol{w},q)\boldsymbol{n})\text{d}\unicode[STIX]{x1D714}+\int _{\unicode[STIX]{x1D6E4}}\frac{\unicode[STIX]{x1D709}}{\unicode[STIX]{x1D709}+\unicode[STIX]{x1D6FE}h}\boldsymbol{h}\cdot \boldsymbol{w}\text{d}\unicode[STIX]{x1D714},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle -\int _{\unicode[STIX]{x1D6E4}}\frac{\unicode[STIX]{x1D6FE}h}{\unicode[STIX]{x1D709}+\unicode[STIX]{x1D6FE}h}\boldsymbol{T}_{f}(\boldsymbol{v},p)\boldsymbol{n}\cdot \boldsymbol{w}\text{d}\unicode[STIX]{x1D714}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad -\int _{\unicode[STIX]{x1D6E4}}\frac{\unicode[STIX]{x1D6FE}h}{\unicode[STIX]{x1D709}+\unicode[STIX]{x1D6FE}h}(\boldsymbol{v}-\boldsymbol{g})\cdot (\boldsymbol{T}_{f}(\boldsymbol{w},q)\boldsymbol{n})\text{d}\unicode[STIX]{x1D714}+\int _{\unicode[STIX]{x1D6E4}}\frac{1}{\unicode[STIX]{x1D709}+\unicode[STIX]{x1D6FE}h}(\boldsymbol{v}-\boldsymbol{g})\cdot \boldsymbol{w}\text{d}\unicode[STIX]{x1D714}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad -\int _{\unicode[STIX]{x1D6E4}}\frac{\unicode[STIX]{x1D709}\unicode[STIX]{x1D6FE}h}{\unicode[STIX]{x1D709}+\unicode[STIX]{x1D6FE}h}(\boldsymbol{T}_{f}(\boldsymbol{v},p)\boldsymbol{n}-\boldsymbol{h})\cdot (\boldsymbol{T}_{f}(\boldsymbol{w},q)\boldsymbol{n})\text{d}\unicode[STIX]{x1D714}+\int _{\unicode[STIX]{x1D6E4}}\frac{\unicode[STIX]{x1D709}}{\unicode[STIX]{x1D709}+\unicode[STIX]{x1D6FE}h}\boldsymbol{h}\cdot \boldsymbol{w}\text{d}\unicode[STIX]{x1D714},\nonumber\end{eqnarray}$$
where
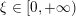 $\unicode[STIX]{x1D709}\in [0,+\infty )$
and
$\unicode[STIX]{x1D709}\in [0,+\infty )$
and
![]() $\unicode[STIX]{x1D6FE}>0$
are two parameters and
$\unicode[STIX]{x1D6FE}>0$
are two parameters and
![]() $h$
is the mesh size (possibly not constant). This discrete problem preserves the usual finite element accuracy. Note that for
$h$
is the mesh size (possibly not constant). This discrete problem preserves the usual finite element accuracy. Note that for
![]() $\unicode[STIX]{x1D709}=0$
we recover the classical Nitsche method to prescribe the Dirichlet condition (7.36a
), whereas for
$\unicode[STIX]{x1D709}=0$
we recover the classical Nitsche method to prescribe the Dirichlet condition (7.36a
), whereas for
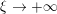 $\unicode[STIX]{x1D709}\rightarrow +\infty$
the formulation is consistent with the Neumann condition (7.36b
). Thus, the idea is to change the value of
$\unicode[STIX]{x1D709}\rightarrow +\infty$
the formulation is consistent with the Neumann condition (7.36b
). Thus, the idea is to change the value of
![]() $\unicode[STIX]{x1D709}$
(
$\unicode[STIX]{x1D709}$
(
![]() $0$
or
$0$
or
![]() $+\infty$
) allowing for the switch between Dirichlet and Neumann conditions. Alternatively, the switch between a flow rate and mean pressure condition could be prescribed via the defective version of the extended Nitsche method proposed in Vergara (Reference Vergara2011).
$+\infty$
) allowing for the switch between Dirichlet and Neumann conditions. Alternatively, the switch between a flow rate and mean pressure condition could be prescribed via the defective version of the extended Nitsche method proposed in Vergara (Reference Vergara2011).
A second family of reduced strategies includes a reduced model of the leaflets without solving the full 3D mechanical problem. These methods are very useful when one wants to determine with a good accuracy the influence of the leaflets on the direction of the fluid jet. A first simple model is based on including the position of the open leaflets obtained by a preliminary mechanical simulation and considering an on–off opening/closure mode: see e.g. Bonomi et al. (Reference Bonomi, Vergara, Faggiano, Stevanella, Conti, Redaelli, Puppini, Faggian, Formaggia and Luciani2015). A similar model has been proposed by Astorino et al. (Reference Astorino, Hamers, Shadden and Gerbeau2012), who consider an immersed resistive approach to switch between the open and closed configuration. In particular, the following term is added to the variational formulation of the fluid problem:
 $$\begin{eqnarray}\int _{\unicode[STIX]{x1D6E4}_{o}}R_{o}\boldsymbol{v}\cdot \boldsymbol{w}\text{d}\unicode[STIX]{x1D6FE}+\int _{\unicode[STIX]{x1D6E4}_{c}}R_{c}\boldsymbol{v}\cdot \boldsymbol{w}\text{d}\unicode[STIX]{x1D6FE},\end{eqnarray}$$
$$\begin{eqnarray}\int _{\unicode[STIX]{x1D6E4}_{o}}R_{o}\boldsymbol{v}\cdot \boldsymbol{w}\text{d}\unicode[STIX]{x1D6FE}+\int _{\unicode[STIX]{x1D6E4}_{c}}R_{c}\boldsymbol{v}\cdot \boldsymbol{w}\text{d}\unicode[STIX]{x1D6FE},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6E4}_{o}$
and
$\unicode[STIX]{x1D6E4}_{o}$
and
![]() $\unicode[STIX]{x1D6E4}_{c}$
are the surfaces representing the open and closed leaflet configurations, respectively, and
$\unicode[STIX]{x1D6E4}_{c}$
are the surfaces representing the open and closed leaflet configurations, respectively, and
![]() $R_{o}$
and
$R_{o}$
and
![]() $R_{c}$
are the corresponding resistance, which act as penalization terms to enforce the no-slip condition
$R_{c}$
are the corresponding resistance, which act as penalization terms to enforce the no-slip condition
![]() $\boldsymbol{v}=\mathbf{0}$
at the leaflet. Thus, when the value of the resistance is high, the corresponding surface configuration is physically included in the model, the velocity is zero at the leaflet and, accordingly, a pressure drop is generated across the leaflet; in contrast, when the value of the resistance is zero, the leaflet is invisible to the model, no constraint is prescribed on the velocity, and no pressure drop is generated. The switch between large and vanishing values of the resistances is determined by (7.34).
$\boldsymbol{v}=\mathbf{0}$
at the leaflet. Thus, when the value of the resistance is high, the corresponding surface configuration is physically included in the model, the velocity is zero at the leaflet and, accordingly, a pressure drop is generated across the leaflet; in contrast, when the value of the resistance is zero, the leaflet is invisible to the model, no constraint is prescribed on the velocity, and no pressure drop is generated. The switch between large and vanishing values of the resistances is determined by (7.34).
More sophisticated models account not only for the open and closed configurations of the leaflets, but also provide a simplified dynamics of the entire valve opening/closure mechanism. For example, Laadhari and Quarteroni (Reference Laadhari and Quarteroni2016) and Fedele, Faggiano, Dede’ and Quarteroni (Reference Fedele, Faggiano, Dede’ and Quarteroni2016) represent a leaflet
![]() $\unicode[STIX]{x1D6E4}$
as a surface described by two embedded level set functions which depend on a single scalar function of time, that is, the opening angle
$\unicode[STIX]{x1D6E4}$
as a surface described by two embedded level set functions which depend on a single scalar function of time, that is, the opening angle
![]() $\unicode[STIX]{x1D703}$
. The latter is determined by a relation very similar to (7.35). At each time step, the term
$\unicode[STIX]{x1D703}$
. The latter is determined by a relation very similar to (7.35). At each time step, the term
 $$\begin{eqnarray}\int _{\unicode[STIX]{x1D6E4}}R(\boldsymbol{v}-\boldsymbol{v}_{\mathit{leaf}})\cdot \boldsymbol{w}\text{d}\unicode[STIX]{x1D6FE}\end{eqnarray}$$
$$\begin{eqnarray}\int _{\unicode[STIX]{x1D6E4}}R(\boldsymbol{v}-\boldsymbol{v}_{\mathit{leaf}})\cdot \boldsymbol{w}\text{d}\unicode[STIX]{x1D6FE}\end{eqnarray}$$
is added to the weak formulation of the fluid problem, in order to guarantee a no-slip condition at the leaflet (
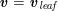 $\boldsymbol{v}=\boldsymbol{v}_{\mathit{leaf}}$
, where
$\boldsymbol{v}=\boldsymbol{v}_{\mathit{leaf}}$
, where
![]() $\boldsymbol{v}_{\mathit{leaf}}$
is the leaflet velocity determined from
$\boldsymbol{v}_{\mathit{leaf}}$
is the leaflet velocity determined from
![]() $\unicode[STIX]{x1D703}$
) by selecting a sufficiently large resistance
$\unicode[STIX]{x1D703}$
) by selecting a sufficiently large resistance
![]() $R$
. A similar approach has recently been adopted in Auricchio et al. (Reference Auricchio, Lefieux, Reali and Veneziani2016), where however the leaflet is represented in a more simplified way by means of the opening angle alone (i.e. no level set functions are involved).
$R$
. A similar approach has recently been adopted in Auricchio et al. (Reference Auricchio, Lefieux, Reali and Veneziani2016), where however the leaflet is represented in a more simplified way by means of the opening angle alone (i.e. no level set functions are involved).
In Figure 7.7 we give an example of the fluid dynamics across the aortic valve obtained by means of the method proposed in Fedele et al. (Reference Fedele, Faggiano, Dede’ and Quarteroni2016).

Figure 7.7. Fluid dynamics in the ascending aorta with a patient-specific aortic valve. Numerical results were obtained using LifeV. See Fedele et al. (Reference Fedele, Faggiano, Dede’ and Quarteroni2016) for a complete overview of the results.
7.4.3 Interaction between blood and leaflets
To accurately model the interaction between blood and valve leaflets, aimed, for example, at detailed computation of the internal leaflet stresses, the solution of a full FSI problem is required.
Unlike for the blood vessel and ventricular simulations, the arbitrary Lagrangian–Eulerian (ALE) formulation, described in Section 4.6, is not suited to handling the FSI problem arising between blood and heart valve leaflets. Indeed, due to the large displacements of the leaflets, the fluid mesh becomes highly distorted, producing severely stretched mesh elements and thus requiring a frequent remeshing of the grid. For this reason, specific FSI techniques have been developed specifically for the numerical solution of this problem. The most successful are the immersed boundary method, the fictitious domain approach and the cut-FEM method, together with their numerous variants. All these methods are characterized by a fixed fluid mesh and enable us to treat non-conforming interface meshes.
Immersed boundary method.
The celebrated immersed boundary method (IB) was specifically developed by Peskin (Reference Peskin1972) for the fluid dynamics in the heart. The leaflets are represented by membranes in a Lagrangian framework regarded as part of the fluid, represented in an Eulerian framework, and exerting internal localized forces on the latter. This is achieved by introducing a Dirac delta distribution,
![]() $\unicode[STIX]{x1D6FF}$
, on the membrane.
$\unicode[STIX]{x1D6FF}$
, on the membrane.
The IB method was originally developed for finite difference spatial discretization: see e.g. Peskin (Reference Peskin1972), Mittal and Iaccarino (Reference Mittal and Iaccarino2005) and Peskin (Reference Peskin2002). In this case, in order to avoid leaks, the Lagrangian grid should be sufficiently fine for the distance between two adjacent points to be less than the Eulerian mesh size. Then, the structural forces are interpolated into the fixed nodes of the fluid mesh. The major issue when finite differences are used is the approximation of
![]() $\unicode[STIX]{x1D6FF}$
. This is usually obtained via a function
$\unicode[STIX]{x1D6FF}$
. This is usually obtained via a function
![]() $\unicode[STIX]{x1D6FF}_{h}$
, which is non-singular for each
$\unicode[STIX]{x1D6FF}_{h}$
, which is non-singular for each
![]() $h$
and tends to
$h$
and tends to
![]() $\unicode[STIX]{x1D6FF}$
for
$\unicode[STIX]{x1D6FF}$
for
![]() $h\rightarrow 0$
(Peskin Reference Peskin2002).
$h\rightarrow 0$
(Peskin Reference Peskin2002).
Here we report the variational formulation of the IB method proposed in Boffi and Gastaldi (Reference Boffi and Gastaldi2003), which is useful for a finite element approximation and does not require any specific approximation of the delta distribution. Given a two-dimensional fluid domain
![]() $\unicode[STIX]{x1D6FA}_{f}$
, let
$\unicode[STIX]{x1D6FA}_{f}$
, let
![]() $\unicode[STIX]{x1D6E4}_{s}$
be the immersed (one-dimensional) structure, whose material points are located at each
$\unicode[STIX]{x1D6E4}_{s}$
be the immersed (one-dimensional) structure, whose material points are located at each
![]() $t$
in
$t$
in
![]() $\boldsymbol{X}(s,t)$
, where
$\boldsymbol{X}(s,t)$
, where
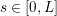 $s\in [0,L]$
is the Lagrangian coordinate. We consider as an example the case of a massless linear elastic structure with elasticity constant
$s\in [0,L]$
is the Lagrangian coordinate. We consider as an example the case of a massless linear elastic structure with elasticity constant
![]() $\unicode[STIX]{x1D705}$
. Thus, referring to the notation introduced in Section 4.1 and assuming homogeneous boundary conditions, the weak formulation of the IB method is as follows (Boffi, Gastaldi and Heltai Reference Boffi, Gastaldi and Heltai2007). For each
$\unicode[STIX]{x1D705}$
. Thus, referring to the notation introduced in Section 4.1 and assuming homogeneous boundary conditions, the weak formulation of the IB method is as follows (Boffi, Gastaldi and Heltai Reference Boffi, Gastaldi and Heltai2007). For each
![]() $t>0$
, find
$t>0$
, find
![]() $\boldsymbol{v}\in \boldsymbol{V}$
,
$\boldsymbol{v}\in \boldsymbol{V}$
,
![]() $\boldsymbol{v}=\boldsymbol{v}_{0}$
for
$\boldsymbol{v}=\boldsymbol{v}_{0}$
for
![]() $t=0$
,
$t=0$
,
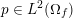 $p\in L^{2}(\unicode[STIX]{x1D6FA}_{f})$
, and
$p\in L^{2}(\unicode[STIX]{x1D6FA}_{f})$
, and
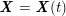 $\boldsymbol{X}=\boldsymbol{X}(t)$
,
$\boldsymbol{X}=\boldsymbol{X}(t)$
,
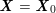 $\boldsymbol{X}=\boldsymbol{X}_{0}$
for
$\boldsymbol{X}=\boldsymbol{X}_{0}$
for
![]() $t=0$
, such that
$t=0$
, such that
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70C}_{f}\int _{\unicode[STIX]{x1D6FA}_{f}}\frac{\unicode[STIX]{x2202}\boldsymbol{v}}{\unicode[STIX]{x2202}t}\cdot \boldsymbol{w}\text{d}\unicode[STIX]{x1D714}+{\mathcal{A}}_{f}(\boldsymbol{v},\boldsymbol{v},\boldsymbol{w})+{\mathcal{B}}(p,\boldsymbol{w})=\int _{0}^{L}\unicode[STIX]{x1D705}\frac{\unicode[STIX]{x2202}^{2}\boldsymbol{X}(s,t)}{\unicode[STIX]{x2202}s^{2}}\boldsymbol{w}(\boldsymbol{X}(s,t))\text{d}s, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70C}_{f}\int _{\unicode[STIX]{x1D6FA}_{f}}\frac{\unicode[STIX]{x2202}\boldsymbol{v}}{\unicode[STIX]{x2202}t}\cdot \boldsymbol{w}\text{d}\unicode[STIX]{x1D714}+{\mathcal{A}}_{f}(\boldsymbol{v},\boldsymbol{v},\boldsymbol{w})+{\mathcal{B}}(p,\boldsymbol{w})=\int _{0}^{L}\unicode[STIX]{x1D705}\frac{\unicode[STIX]{x2202}^{2}\boldsymbol{X}(s,t)}{\unicode[STIX]{x2202}s^{2}}\boldsymbol{w}(\boldsymbol{X}(s,t))\text{d}s, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{B}}(q,\boldsymbol{v})=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{B}}(q,\boldsymbol{v})=0, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{X}}{\unicode[STIX]{x2202}t}(s,t)=\boldsymbol{v}(\boldsymbol{X}(s,t),t), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{X}}{\unicode[STIX]{x2202}t}(s,t)=\boldsymbol{v}(\boldsymbol{X}(s,t),t), & \displaystyle\end{eqnarray}$$
 $q\in L^{2}(\unicode[STIX]{x1D6FA}_{f})$
. In fact, the right-hand side of (7.37a
) guarantees the satisfaction of the normal stress continuity at the membrane, whereas (7.37c
) is the velocity continuity.
$q\in L^{2}(\unicode[STIX]{x1D6FA}_{f})$
. In fact, the right-hand side of (7.37a
) guarantees the satisfaction of the normal stress continuity at the membrane, whereas (7.37c
) is the velocity continuity.
For the finite element approximation of the above problem, the forcing term is usually integrated by parts. For example, in the case of linear finite elements for the structure, for each
![]() $t>0$
it becomes
$t>0$
it becomes
 $$\begin{eqnarray}\mathop{\sum }_{i=0}^{M-1}\unicode[STIX]{x1D705}\biggl(\frac{\unicode[STIX]{x2202}\boldsymbol{X}_{h}^{i+1}}{\unicode[STIX]{x2202}s}-\frac{\unicode[STIX]{x2202}\boldsymbol{X}_{h}^{i}}{\unicode[STIX]{x2202}s}\biggr)\boldsymbol{w}(\boldsymbol{X}_{h}^{i})\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{i=0}^{M-1}\unicode[STIX]{x1D705}\biggl(\frac{\unicode[STIX]{x2202}\boldsymbol{X}_{h}^{i+1}}{\unicode[STIX]{x2202}s}-\frac{\unicode[STIX]{x2202}\boldsymbol{X}_{h}^{i}}{\unicode[STIX]{x2202}s}\biggr)\boldsymbol{w}(\boldsymbol{X}_{h}^{i})\end{eqnarray}$$
(Boffi et al.
Reference Boffi, Gastaldi and Heltai2007), where
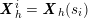 $\boldsymbol{X}_{h}^{i}=\boldsymbol{X}_{h}(s_{i})$
,
$\boldsymbol{X}_{h}^{i}=\boldsymbol{X}_{h}(s_{i})$
,
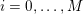 $i=0,\ldots ,M$
, is the finite element approximation of
$i=0,\ldots ,M$
, is the finite element approximation of
![]() $\boldsymbol{X}$
and
$\boldsymbol{X}$
and
![]() $s_{i}$
are the nodes of the one-dimensional mesh.
$s_{i}$
are the nodes of the one-dimensional mesh.
Regarding the time discretization, a first approach is to consider a fully implicit scheme. For the backward Euler approximation, unconditional stability is guaranteed (Tu and Peskin Reference Tu and Peskin1992). However, this scheme requires the introduction of sub-iterations to handle the coupling between fluid and structure in (7.37). A more useful approach relies on treating the right-hand side of (7.37a ) explicitly and the remaining part of the equation implicitly. The position occupied by the structure is then updated in a second step by means of a suitable implicit approximation of (7.37c ). This scheme has been proved to be stable under a CFL-like condition (Boffi et al. Reference Boffi, Gastaldi and Heltai2007).
Several extensions and applications of the IB method have been provided. Among them, we mention the following: the variational formulation for the case of a thick immersed structure proposed in Boffi et al. (Reference Boffi, Gastaldi, Heltai and Peskin2008), where the right-hand side of (7.37a ) becomes
 $$\begin{eqnarray}\int _{\unicode[STIX]{x1D6FA}_{s}}\widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}}(\boldsymbol{s},t)):\unicode[STIX]{x1D6FB}\boldsymbol{w}(\boldsymbol{X}(\boldsymbol{s},t))\text{d}\boldsymbol{s},\end{eqnarray}$$
$$\begin{eqnarray}\int _{\unicode[STIX]{x1D6FA}_{s}}\widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}}(\boldsymbol{s},t)):\unicode[STIX]{x1D6FB}\boldsymbol{w}(\boldsymbol{X}(\boldsymbol{s},t))\text{d}\boldsymbol{s},\end{eqnarray}$$
where
![]() $\boldsymbol{s}$
in this case is a vectorial Lagrangian coordinate; a mesh-adaptive approach used in combination with a second-order scheme (see Griffith et al. Reference Griffith, Hornung, Mcqueen and Peskin2007); the use of a curvilinear fixed fluid mesh to improve flexibility and efficiency (the CURVIB approach: see Borazjani, Ge and Sotiropoulos Reference Borazjani, Ge and Sotiropoulos2008); the application to realistic three-dimensional mitral and aortic valves successfully addressed in Griffith et al. (Reference Griffith, Luo, Mcqueen and Peskin2009) and Yin et al. (Reference Yin, Luo, Wang and Watton2009).
$\boldsymbol{s}$
in this case is a vectorial Lagrangian coordinate; a mesh-adaptive approach used in combination with a second-order scheme (see Griffith et al. Reference Griffith, Hornung, Mcqueen and Peskin2007); the use of a curvilinear fixed fluid mesh to improve flexibility and efficiency (the CURVIB approach: see Borazjani, Ge and Sotiropoulos Reference Borazjani, Ge and Sotiropoulos2008); the application to realistic three-dimensional mitral and aortic valves successfully addressed in Griffith et al. (Reference Griffith, Luo, Mcqueen and Peskin2009) and Yin et al. (Reference Yin, Luo, Wang and Watton2009).
Fictitious domain approach.
The fictitious domain (FD) approach was first introduced by Glowinski, Pan and Periaux (Reference Glowinski, Pan and Periaux1997) and Bertrand, Tanguy and Thibault (Reference Bertrand, Tanguy and Thibault1997), and then used by de Hart et al. (Reference de Hart, Peters, Schreurs and Baaijens2000) and de Hart et al. (Reference de Hart, Baaijens, Peters and Schreurs2003) in the context of heart valves. The FD approach can be regarded as the dual of the IB method, in the sense that in the latter a weak enforcement of the normal stress continuity at the FS interface is added to the weak formulation of fluid problem, whereas in the FD approach the velocity continuity is weakly enforced at the FS interface. This is achieved by means of Lagrange multipliers, as detailed in what follows (we refer to Sections 4.1, 4.2 and 4.3 for the notation; in particular, variables with ![]() are referred to the referencedomain, and we assume homogeneous boundary conditions). Find
are referred to the referencedomain, and we assume homogeneous boundary conditions). Find
 $$\begin{eqnarray}\boldsymbol{v}(t)\in \boldsymbol{V}^{t},\quad \widehat{\boldsymbol{d}}(t)\in \boldsymbol{D},\quad \boldsymbol{\unicode[STIX]{x1D706}}(t)\in \boldsymbol{H}^{-1/2}(\unicode[STIX]{x1D6F4}^{t})\quad \text{and}\quad p(t)\in L^{2}(\unicode[STIX]{x1D6FA}_{f}^{t}),\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{v}(t)\in \boldsymbol{V}^{t},\quad \widehat{\boldsymbol{d}}(t)\in \boldsymbol{D},\quad \boldsymbol{\unicode[STIX]{x1D706}}(t)\in \boldsymbol{H}^{-1/2}(\unicode[STIX]{x1D6F4}^{t})\quad \text{and}\quad p(t)\in L^{2}(\unicode[STIX]{x1D6FA}_{f}^{t}),\end{eqnarray}$$
such that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D70C}_{f}\int _{\unicode[STIX]{x1D6FA}_{f}^{t}}\frac{\unicode[STIX]{x2202}\boldsymbol{v}}{\unicode[STIX]{x2202}t}\cdot \boldsymbol{w}\text{d}\unicode[STIX]{x1D714}+{\mathcal{A}}_{f}(\boldsymbol{v},\boldsymbol{v},\boldsymbol{w})+{\mathcal{B}}(p,\boldsymbol{w})\nonumber\\ \displaystyle & & \displaystyle \quad +\,\unicode[STIX]{x1D70C}_{s}\int _{\unicode[STIX]{x1D6FA}_{s}}\frac{\unicode[STIX]{x2202}^{2}\widehat{\boldsymbol{d}}}{\unicode[STIX]{x2202}t^{2}}\cdot \widehat{\boldsymbol{e}}\text{d}\unicode[STIX]{x1D714}+\int _{\unicode[STIX]{x1D6FA}_{s}}\widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}}):\unicode[STIX]{x1D6FB}\widehat{\boldsymbol{e}}\text{d}\unicode[STIX]{x1D714}=\int _{\unicode[STIX]{x1D6F4}^{t}}\boldsymbol{\unicode[STIX]{x1D706}}\cdot (\boldsymbol{w}-\boldsymbol{e})\text{d}\unicode[STIX]{x1D70E},\nonumber\\ \displaystyle & & \displaystyle {\mathcal{B}}(q,\boldsymbol{v})=0,\nonumber\\ \displaystyle & & \displaystyle \int _{\unicode[STIX]{x1D6F4}^{t}}\boldsymbol{\unicode[STIX]{x1D707}}\cdot \biggl(\boldsymbol{v}-\frac{\unicode[STIX]{x2202}\boldsymbol{d}}{\unicode[STIX]{x2202}t}\biggr)\text{d}\unicode[STIX]{x1D70E}=0,\nonumber\\ \displaystyle & & \displaystyle \boldsymbol{d}_{f}=\boldsymbol{d}\quad \text{at }\unicode[STIX]{x1D6F4}^{t},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D70C}_{f}\int _{\unicode[STIX]{x1D6FA}_{f}^{t}}\frac{\unicode[STIX]{x2202}\boldsymbol{v}}{\unicode[STIX]{x2202}t}\cdot \boldsymbol{w}\text{d}\unicode[STIX]{x1D714}+{\mathcal{A}}_{f}(\boldsymbol{v},\boldsymbol{v},\boldsymbol{w})+{\mathcal{B}}(p,\boldsymbol{w})\nonumber\\ \displaystyle & & \displaystyle \quad +\,\unicode[STIX]{x1D70C}_{s}\int _{\unicode[STIX]{x1D6FA}_{s}}\frac{\unicode[STIX]{x2202}^{2}\widehat{\boldsymbol{d}}}{\unicode[STIX]{x2202}t^{2}}\cdot \widehat{\boldsymbol{e}}\text{d}\unicode[STIX]{x1D714}+\int _{\unicode[STIX]{x1D6FA}_{s}}\widehat{\boldsymbol{T}}_{s}(\widehat{\boldsymbol{d}}):\unicode[STIX]{x1D6FB}\widehat{\boldsymbol{e}}\text{d}\unicode[STIX]{x1D714}=\int _{\unicode[STIX]{x1D6F4}^{t}}\boldsymbol{\unicode[STIX]{x1D706}}\cdot (\boldsymbol{w}-\boldsymbol{e})\text{d}\unicode[STIX]{x1D70E},\nonumber\\ \displaystyle & & \displaystyle {\mathcal{B}}(q,\boldsymbol{v})=0,\nonumber\\ \displaystyle & & \displaystyle \int _{\unicode[STIX]{x1D6F4}^{t}}\boldsymbol{\unicode[STIX]{x1D707}}\cdot \biggl(\boldsymbol{v}-\frac{\unicode[STIX]{x2202}\boldsymbol{d}}{\unicode[STIX]{x2202}t}\biggr)\text{d}\unicode[STIX]{x1D70E}=0,\nonumber\\ \displaystyle & & \displaystyle \boldsymbol{d}_{f}=\boldsymbol{d}\quad \text{at }\unicode[STIX]{x1D6F4}^{t},\end{eqnarray}$$
for all
![]() $\boldsymbol{w}\in \boldsymbol{V}$
,
$\boldsymbol{w}\in \boldsymbol{V}$
,
![]() $\widehat{\boldsymbol{e}}\in \boldsymbol{D}$
,
$\widehat{\boldsymbol{e}}\in \boldsymbol{D}$
,
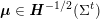 $\boldsymbol{\unicode[STIX]{x1D707}}\in \boldsymbol{H}^{-1/2}(\unicode[STIX]{x1D6F4}^{t})$
and
$\boldsymbol{\unicode[STIX]{x1D707}}\in \boldsymbol{H}^{-1/2}(\unicode[STIX]{x1D6F4}^{t})$
and
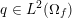 $q\in L^{2}(\unicode[STIX]{x1D6FA}_{f})$
. For the well-posedness of the time-discretized version of problem (7.38) we refer to Formaggia et al. (Reference Formaggia, Veneziani and Vergara2009b
). We notice that the use of the same Lagrange multiplier
$q\in L^{2}(\unicode[STIX]{x1D6FA}_{f})$
. For the well-posedness of the time-discretized version of problem (7.38) we refer to Formaggia et al. (Reference Formaggia, Veneziani and Vergara2009b
). We notice that the use of the same Lagrange multiplier
![]() $\boldsymbol{\unicode[STIX]{x1D706}}$
from both the fluid and structure sides also guarantees the continuity of normal stresses (Formaggia et al.
Reference Formaggia, Veneziani and Vergara2009b
).
$\boldsymbol{\unicode[STIX]{x1D706}}$
from both the fluid and structure sides also guarantees the continuity of normal stresses (Formaggia et al.
Reference Formaggia, Veneziani and Vergara2009b
).
Stijnen et al. (Reference Stijnen, de Hart, Bovendeerd and van de Vosse2004) have successfully reported a validation with experimental measurements, and Astorino et al. (Reference Astorino, Gerbeau, Pantz and Traoré2010) have reported an application of the FD approach to three-dimensional problems in combination with a contact model for the leaflets.
Cut-FEM approach.
A natural strategy for handling an internal interface cutting the mesh in an arbitrary way is to write two weak formulations of the problem at hand, one for each of the two subdomains generated by the presence of the interface, and then sum them up. In this case, the meshes of the two subdomains are fixed (background meshes). Since some of the mesh elements are cut by the interface, their contribution to the matrices is split into two parts: see Figure 7.8(a). This method is known as cut-FEM (Hansbo and Hansbo Reference Hansbo and Hansbo2002, Hansbo, Hansbo and Larson Reference Hansbo, Hansbo and Larson2003). Here, the jump between the normal stresses at the interface is determined by the physical interaction with the interface, as happens for the blood/valve interaction.

Figure 7.8. Element mesh
![]() $K$
cut by the interface
$K$
cut by the interface
![]() $\unicode[STIX]{x1D6E4}$
(a) and FS domain (b). For the latter, we notice that
$\unicode[STIX]{x1D6E4}$
(a) and FS domain (b). For the latter, we notice that
![]() $\unicode[STIX]{x1D6FA}_{f}^{1}$
and
$\unicode[STIX]{x1D6FA}_{f}^{1}$
and
![]() $\unicode[STIX]{x1D6FA}_{f}^{2}$
are two non-overlapping subdomains, whereas the related computational meshes have an overlap (in grey) in view of the X-FEM approach.
$\unicode[STIX]{x1D6FA}_{f}^{2}$
are two non-overlapping subdomains, whereas the related computational meshes have an overlap (in grey) in view of the X-FEM approach.
A common strategy used to guarantee the satisfaction of the interface continuity conditions is discontinuous Galerkin (DG) mortaring (often referred to as Nitsche mortaring). This is a very effective choice since the DG method prescribes interface conditions in a weak sense, thus allowing a great degree of flexibility of the solution at the interface (Hansbo and Hansbo Reference Hansbo and Hansbo2002, Hansbo et al. Reference Hansbo, Hansbo and Larson2003).
Finally, we notice that the implementation of the cut-FEM method is not standard since in the cut elements we may have polygonal elements: see for example Figure 7.8(a), where the original triangle is split into a triangle and a trapezoid. A solution is offered by the extended finite element method (X-FEM), where the finite element space is suitably enriched in order to make the treatment of the cut elements easy. In particular, the basic idea is to duplicate the variables in the cut elements and to use the basis functions of the original triangle in both subdomains, to represent the finite element solution and to compute the integrals (Hansbo and Hansbo Reference Hansbo and Hansbo2002).
To provide a concrete example of the cut-FEM method, we will give the weak formulation introduced and analysed by Alauzet, Fabrèges, Fernández and Landajuela (Reference Alauzet, Fabrèges, Fernández and Landajuela2016), related to the case of a valve embedded in blood and represented by
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{s}H_{s}\frac{\unicode[STIX]{x2202}\boldsymbol{d}}{\unicode[STIX]{x2202}t}+\boldsymbol{L}\boldsymbol{d}=-[\![\boldsymbol{T}_{f}\boldsymbol{n}]\!]\quad \text{in }\unicode[STIX]{x1D6F4},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{s}H_{s}\frac{\unicode[STIX]{x2202}\boldsymbol{d}}{\unicode[STIX]{x2202}t}+\boldsymbol{L}\boldsymbol{d}=-[\![\boldsymbol{T}_{f}\boldsymbol{n}]\!]\quad \text{in }\unicode[STIX]{x1D6F4},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6F4}$
is the embedded membrane,
$\unicode[STIX]{x1D6F4}$
is the embedded membrane,
![]() $\boldsymbol{L}$
is an elliptic operator, and
$\boldsymbol{L}$
is an elliptic operator, and
![]() $[\![\cdot ]\!]$
denotes the jump across the membrane. In particular, referring to Figure 7.8(b), let
$[\![\cdot ]\!]$
denotes the jump across the membrane. In particular, referring to Figure 7.8(b), let
![]() $\unicode[STIX]{x1D6FA}_{f}^{1}$
and
$\unicode[STIX]{x1D6FA}_{f}^{1}$
and
![]() $\unicode[STIX]{x1D6FA}_{f}^{2}$
be two non-overlapping subdomains separated by
$\unicode[STIX]{x1D6FA}_{f}^{2}$
be two non-overlapping subdomains separated by
![]() $\unicode[STIX]{x1D6F4}$
, and
$\unicode[STIX]{x1D6F4}$
, and
![]() $\unicode[STIX]{x1D6FA}_{f,h}^{1}$
and
$\unicode[STIX]{x1D6FA}_{f,h}^{1}$
and
![]() $\unicode[STIX]{x1D6FA}_{f,h}^{2}$
two meshes containing
$\unicode[STIX]{x1D6FA}_{f,h}^{2}$
two meshes containing
![]() $\unicode[STIX]{x1D6FA}_{f}^{1}$
and
$\unicode[STIX]{x1D6FA}_{f}^{1}$
and
![]() $\unicode[STIX]{x1D6FA}_{f}^{2}$
, respectively, with an overlap region (in grey in the figure) containing the membrane. Moreover, let
$\unicode[STIX]{x1D6FA}_{f}^{2}$
, respectively, with an overlap region (in grey in the figure) containing the membrane. Moreover, let
![]() $\boldsymbol{V}_{h}^{i}$
and
$\boldsymbol{V}_{h}^{i}$
and
![]() $Q_{h}^{i}$
be velocity and pressure finite element spaces related to
$Q_{h}^{i}$
be velocity and pressure finite element spaces related to
![]() $\unicode[STIX]{x1D6FA}_{f,h}^{i}$
and let
$\unicode[STIX]{x1D6FA}_{f,h}^{i}$
and let
![]() ${\mathcal{C}}^{i}$
be one of the bilinear or trilinear forms
${\mathcal{C}}^{i}$
be one of the bilinear or trilinear forms
![]() ${\mathcal{C}}$
introduced in Section 2 restricted to
${\mathcal{C}}$
introduced in Section 2 restricted to
![]() $\unicode[STIX]{x1D6FA}_{f,h}^{i}$
. Thus we have
$\unicode[STIX]{x1D6FA}_{f,h}^{i}$
. Thus we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{i=1}^{2}\biggl[\unicode[STIX]{x1D70C}_{f}\int _{\unicode[STIX]{x1D6FA}_{f}^{i}}\frac{\unicode[STIX]{x2202}\boldsymbol{v}_{h}^{i}}{\unicode[STIX]{x2202}t}\cdot \boldsymbol{w}\text{d}\unicode[STIX]{x1D714}+{\mathcal{A}}_{f}^{i}(\boldsymbol{v}_{h}^{i},\boldsymbol{v}_{h}^{i},\boldsymbol{w})+{\mathcal{B}}^{i}(p_{h}^{i},\boldsymbol{w})-{\mathcal{B}}^{i}(q,\boldsymbol{v}_{h}^{i})\biggr]\nonumber\\ \displaystyle & & \displaystyle \quad +\,s_{h}(\boldsymbol{v}_{h},\boldsymbol{w})+\unicode[STIX]{x1D70C}_{s}H_{s}\int _{\unicode[STIX]{x1D6F4}}\frac{\unicode[STIX]{x2202}\boldsymbol{d}_{h}}{\unicode[STIX]{x2202}t}\cdot \boldsymbol{e}\text{d}\unicode[STIX]{x1D70E}+\int _{\unicode[STIX]{x1D6F4}}\boldsymbol{L}\boldsymbol{d}_{h}\cdot \boldsymbol{e}\text{d}\unicode[STIX]{x1D70E}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\mathop{\sum }_{i=1}^{2} [-\int _{\unicode[STIX]{x1D6F4}}\boldsymbol{T}_{f}(\boldsymbol{v}_{h}^{i},p_{h}^{i})\boldsymbol{n}^{i}\cdot (\boldsymbol{w}-\boldsymbol{e})\text{d}\unicode[STIX]{x1D70E}-\int _{\unicode[STIX]{x1D6F4}}\boldsymbol{T}_{f}(\boldsymbol{w},q)\boldsymbol{n}^{i}\cdot \biggl(\boldsymbol{v}_{h}^{i}-\frac{\unicode[STIX]{x2202}\boldsymbol{d}_{h}}{\unicode[STIX]{x2202}t}\biggr)\text{d}\unicode[STIX]{x1D70E}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{\unicode[STIX]{x1D6FE}}{h}\int _{\unicode[STIX]{x1D6F4}}\biggl(\boldsymbol{v}_{h}^{i}-\frac{\unicode[STIX]{x2202}\boldsymbol{d}_{h}}{\unicode[STIX]{x2202}t}\biggr)\cdot (\boldsymbol{w}-\boldsymbol{e})\text{d}\unicode[STIX]{x1D70E}]=0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{i=1}^{2}\biggl[\unicode[STIX]{x1D70C}_{f}\int _{\unicode[STIX]{x1D6FA}_{f}^{i}}\frac{\unicode[STIX]{x2202}\boldsymbol{v}_{h}^{i}}{\unicode[STIX]{x2202}t}\cdot \boldsymbol{w}\text{d}\unicode[STIX]{x1D714}+{\mathcal{A}}_{f}^{i}(\boldsymbol{v}_{h}^{i},\boldsymbol{v}_{h}^{i},\boldsymbol{w})+{\mathcal{B}}^{i}(p_{h}^{i},\boldsymbol{w})-{\mathcal{B}}^{i}(q,\boldsymbol{v}_{h}^{i})\biggr]\nonumber\\ \displaystyle & & \displaystyle \quad +\,s_{h}(\boldsymbol{v}_{h},\boldsymbol{w})+\unicode[STIX]{x1D70C}_{s}H_{s}\int _{\unicode[STIX]{x1D6F4}}\frac{\unicode[STIX]{x2202}\boldsymbol{d}_{h}}{\unicode[STIX]{x2202}t}\cdot \boldsymbol{e}\text{d}\unicode[STIX]{x1D70E}+\int _{\unicode[STIX]{x1D6F4}}\boldsymbol{L}\boldsymbol{d}_{h}\cdot \boldsymbol{e}\text{d}\unicode[STIX]{x1D70E}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\mathop{\sum }_{i=1}^{2} [-\int _{\unicode[STIX]{x1D6F4}}\boldsymbol{T}_{f}(\boldsymbol{v}_{h}^{i},p_{h}^{i})\boldsymbol{n}^{i}\cdot (\boldsymbol{w}-\boldsymbol{e})\text{d}\unicode[STIX]{x1D70E}-\int _{\unicode[STIX]{x1D6F4}}\boldsymbol{T}_{f}(\boldsymbol{w},q)\boldsymbol{n}^{i}\cdot \biggl(\boldsymbol{v}_{h}^{i}-\frac{\unicode[STIX]{x2202}\boldsymbol{d}_{h}}{\unicode[STIX]{x2202}t}\biggr)\text{d}\unicode[STIX]{x1D70E}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{\unicode[STIX]{x1D6FE}}{h}\int _{\unicode[STIX]{x1D6F4}}\biggl(\boldsymbol{v}_{h}^{i}-\frac{\unicode[STIX]{x2202}\boldsymbol{d}_{h}}{\unicode[STIX]{x2202}t}\biggr)\cdot (\boldsymbol{w}-\boldsymbol{e})\text{d}\unicode[STIX]{x1D70E}]=0.\nonumber\end{eqnarray}$$
The terms in the third and fourth rows above are simply the usual DG terms guaranteeing consistency, symmetry and stability of the method, whereas
![]() $s_{h}(\cdot ,\cdot )$
accounts for the ghost node stabilization (Burman et al.
Reference Burman, Claus, Hansbo, Larson and Massing2015), which guarantees an optimal convergence order. This formulation was introduced for infinitesimal displacements. However, the authors also treat the case of a moving interface: for details see Alauzet et al. (Reference Alauzet, Fabrèges, Fernández and Landajuela2016).
$s_{h}(\cdot ,\cdot )$
accounts for the ghost node stabilization (Burman et al.
Reference Burman, Claus, Hansbo, Larson and Massing2015), which guarantees an optimal convergence order. This formulation was introduced for infinitesimal displacements. However, the authors also treat the case of a moving interface: for details see Alauzet et al. (Reference Alauzet, Fabrèges, Fernández and Landajuela2016).
Finally, we notice that the cut-FEM approach has been also considered for the case of a thick structure: see Burman and Fernández (Reference Burman and Fernández2014) and Zonca, Formaggia and Vergara (Reference Zonca, Formaggia and Vergara2016).
7.5 Modelling the entire heart function
We conclude this section by providing some hints on the modelling of the complete heart function, a challenging and far-reaching endeavour. The latter is very complex and requires us to merge all the mathematical, numerical and computational issues highlighted previously in this section: see Lee et al. (Reference Lee, Cookson, Roy, Kerfoot, Asner, Vigueras, Sochi, Deparis, Michler, Smith and Nordsletten2016), Chabiniok et al. (Reference Chabiniok, Wang, Hadjicharalambous, Asner, Lee, Sermesant, Kuhl, Young, Moireau, Nash, Chapelle and Nordsletten2016), Nordsletten et al. (Reference Nordsletten, Niederer, Nash, Hunter and Smith2011b ) and Quarteroni et al. (Reference Quarteroni, Lassila, Rossi and Ruiz-Baier2017).
Basically, an integrated model of the heart involves the coupling of the electromechanical problem (7.31), the blood fluid dynamics (see Section 7.3), and the valve functioning (see Section 7.4). The coupling between the first two subproblems occurs at the endocardium
![]() $\unicode[STIX]{x1D6F4}_{\mathit{endo}}$
: see Figure 6.1. In particular, this is determined by the classical fluid–structure interaction coupling conditions, i.e., the kinematic condition (4.19c
) and the dynamic condition (4.19d
). In particular, referring to the notation of Sections 4.1 and 7.2 and to Figure 6.1, we have the following problem. Find the blood velocity
$\unicode[STIX]{x1D6F4}_{\mathit{endo}}$
: see Figure 6.1. In particular, this is determined by the classical fluid–structure interaction coupling conditions, i.e., the kinematic condition (4.19c
) and the dynamic condition (4.19d
). In particular, referring to the notation of Sections 4.1 and 7.2 and to Figure 6.1, we have the following problem. Find the blood velocity
![]() $\boldsymbol{v}$
and pressure
$\boldsymbol{v}$
and pressure
![]() $p$
, the muscle displacement
$p$
, the muscle displacement
![]() $\boldsymbol{d}$
, the trans-membrane potential
$\boldsymbol{d}$
, the trans-membrane potential
![]() $V_{m}$
, the gating variables
$V_{m}$
, the gating variables
![]() $\boldsymbol{w}$
, and the ionic concentration variables
$\boldsymbol{w}$
, and the ionic concentration variables
![]() $\boldsymbol{c}$
, such that
$\boldsymbol{c}$
, such that
 $$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D70C}_{f}\biggl(\frac{\unicode[STIX]{x2202}\boldsymbol{v}}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D70C}_{f}(\boldsymbol{v}\cdot \unicode[STIX]{x1D6FB})\boldsymbol{v}\biggr)-\unicode[STIX]{x1D6FB}\cdot \boldsymbol{T}_{f}(\boldsymbol{v},p)=\mathbf{0} & & \displaystyle \quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{cav}}^{t},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D70C}_{f}\biggl(\frac{\unicode[STIX]{x2202}\boldsymbol{v}}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D70C}_{f}(\boldsymbol{v}\cdot \unicode[STIX]{x1D6FB})\boldsymbol{v}\biggr)-\unicode[STIX]{x1D6FB}\cdot \boldsymbol{T}_{f}(\boldsymbol{v},p)=\mathbf{0} & & \displaystyle \quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{cav}}^{t},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D6FB}\cdot \boldsymbol{v}=0 & & \displaystyle \quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{cav}}^{t},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D6FB}\cdot \boldsymbol{v}=0 & & \displaystyle \quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{cav}}^{t},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{v}=\frac{\unicode[STIX]{x2202}\boldsymbol{d}}{\unicode[STIX]{x2202}t} & & \displaystyle \quad \text{at }\unicode[STIX]{x1D6F4}_{\mathit{endo}}^{t},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{v}=\frac{\unicode[STIX]{x2202}\boldsymbol{d}}{\unicode[STIX]{x2202}t} & & \displaystyle \quad \text{at }\unicode[STIX]{x1D6F4}_{\mathit{endo}}^{t},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle \biggl(\boldsymbol{T}_{s}^{P}(\boldsymbol{d})+\boldsymbol{T}_{s}^{A}\biggl(\boldsymbol{c},\boldsymbol{d},\frac{\text{d}\boldsymbol{d}}{\text{d}t}\biggr)\biggr)\boldsymbol{n}=\boldsymbol{T}_{f}(\boldsymbol{v},p)\,\boldsymbol{n} & & \displaystyle \quad \text{at }\unicode[STIX]{x1D6F4}_{\mathit{endo}}^{t},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \biggl(\boldsymbol{T}_{s}^{P}(\boldsymbol{d})+\boldsymbol{T}_{s}^{A}\biggl(\boldsymbol{c},\boldsymbol{d},\frac{\text{d}\boldsymbol{d}}{\text{d}t}\biggr)\biggr)\boldsymbol{n}=\boldsymbol{T}_{f}(\boldsymbol{v},p)\,\boldsymbol{n} & & \displaystyle \quad \text{at }\unicode[STIX]{x1D6F4}_{\mathit{endo}}^{t},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D6FB}\cdot \biggl(\widehat{\boldsymbol{T}}_{s}^{P}(\widehat{\boldsymbol{d}})+\widehat{\boldsymbol{T}}_{s}^{A}\biggl(\widehat{\boldsymbol{c}},\widehat{\boldsymbol{d}},\frac{\text{d}\widehat{\boldsymbol{d}}}{\text{d}t}\biggr)\biggr)=\mathbf{0} & & \displaystyle \quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D6FB}\cdot \biggl(\widehat{\boldsymbol{T}}_{s}^{P}(\widehat{\boldsymbol{d}})+\widehat{\boldsymbol{T}}_{s}^{A}\biggl(\widehat{\boldsymbol{c}},\widehat{\boldsymbol{d}},\frac{\text{d}\widehat{\boldsymbol{d}}}{\text{d}t}\biggr)\biggr)=\mathbf{0} & & \displaystyle \quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle \widehat{\boldsymbol{T}}_{s}^{A}=P^{A}\boldsymbol{a}_{f}\otimes \widehat{\boldsymbol{a}}_{f},\quad P^{A}={\mathcal{A}}\biggl(\widehat{\boldsymbol{c}},\widehat{\boldsymbol{d}},\frac{\text{d}\widehat{\boldsymbol{d}}}{\text{d}t}\biggr) & & \displaystyle \quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \widehat{\boldsymbol{T}}_{s}^{A}=P^{A}\boldsymbol{a}_{f}\otimes \widehat{\boldsymbol{a}}_{f},\quad P^{A}={\mathcal{A}}\biggl(\widehat{\boldsymbol{c}},\widehat{\boldsymbol{d}},\frac{\text{d}\widehat{\boldsymbol{d}}}{\text{d}t}\biggr) & & \displaystyle \quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle \widehat{V}_{m}={\mathcal{M}}(\widehat{V}_{m};\widehat{\boldsymbol{d}},\widehat{\boldsymbol{w}},\widehat{\boldsymbol{c}}) & & \displaystyle \quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \widehat{V}_{m}={\mathcal{M}}(\widehat{V}_{m};\widehat{\boldsymbol{d}},\widehat{\boldsymbol{w}},\widehat{\boldsymbol{c}}) & & \displaystyle \quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle (\widehat{\boldsymbol{w}},\widehat{\boldsymbol{c}})={\mathcal{G}}(\widehat{\boldsymbol{w}},\widehat{\boldsymbol{c}};\widehat{V}_{m}) & & \displaystyle \quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle (\widehat{\boldsymbol{w}},\widehat{\boldsymbol{c}})={\mathcal{G}}(\widehat{\boldsymbol{w}},\widehat{\boldsymbol{c}};\widehat{V}_{m}) & & \displaystyle \quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}.\end{eqnarray}$$
After numerical discretization in time and space, the corresponding non-linear algebraic system is tremendously stiff and can have a very high numerical dimension. Devising efficient numerical strategies for its solution is a very active research area.
An effective strategy to solve the entire heart coupled problem numerically is given by the iterative solution at each time step of the electromechanical and fluid subproblems and based on the exchange of the interface conditions (7.39c , 7.39d ). In particular, one of the partitioned strategies described in Section 4.6.3 can be adapted and used for problem (7.39) as well. Of course, at each iteration of the partitioned algorithm, the electromechanical problem could be solved by means of one of the strategies reported in Section 7.2.
Another partitioned algorithm for the solution of problem (7.39) is obtained by considering the solution at each time step of the electrical problem first and the FSI problem later (Nordsletten et al.
Reference Nordsletten, Niederer, Nash, Hunter and Smith2011b
). This is simply an extension of Algorithms EM1 and EM1
![]() $^{\prime }$
reported in Section 7.2, where steps (2b) and (2
$^{\prime }$
reported in Section 7.2, where steps (2b) and (2
![]() $^{\prime }$
b) are replaced by a Newton iteration over the FSI problem.
$^{\prime }$
b) are replaced by a Newton iteration over the FSI problem.
A different approach is based on the monolithic solution of the integrated heart problem (7.39) by means of a full Newton method. In particular, Quarteroni et al. (Reference Quarteroni, Lassila, Rossi and Ruiz-Baier2017) describe fully implicit and semi-implicit methods. The latter is based on updating only a part of the Jacobian as a consequence of an operator splitting technique. By means of numerical experiments, the authors emphasized that particular choices of the splitting and of the temporal scheme could lead to numerical instabilities. Whatever strategy is adopted, the tangent problem at each Newton iteration is solved by means of a preconditioned iterative method, which in this case is particularly suitable due to the block structure of the Jacobian: see Quarteroni et al. (Reference Quarteroni, Lassila, Rossi and Ruiz-Baier2017).
Stability and convergence analysis of the different approaches is a field of current investigation.
PART THREE
Optimization, control, uncertainty and complexity reduction
8 Beyond direct simulation
In all the problems considered so far, for a given set of inputs (e.g. geometry, source terms, boundary and initial conditions) the goal has been to solve a forward PDE problem numerically, and, possibly, to evaluate some physical indices of clinical interest, such as the flow rate across a vessel section, the wall shear stress over a portion of the lumen boundary, or the oscillatory shear index. On the other hand, the efficient numerical algorithms and computational resources now available enable us to tackle several additional kinds of problem.
When simulating blood flows one has to deal with the variability of input data, such as geometric features of the vessel, boundary conditions and physical coefficients (e.g. the Reynolds number, the Womersley number, the structural model or material parameters related to the vessel wall). Very often, these data vary within a broad range and are almost impossible to characterize precisely. All these inputs affect the solution of the problem under investigation, as well as the outcomes of clinical interest. In the clinical context it is thus important to be able to characterize input/output relationships efficiently, in order to investigate both intra-patient and inter-patient variability. For the former case we include all those effects due to variations affecting a single patient, for example over time, or before/after clinical intervention. For the latter case, we mention for instance the morphological variability among vessel shapes due to age, size or pathological factors (see e.g. Xiong and Chong Reference Xiong and Chong2008 for the case of distal coronary anastomoses). It is thus of paramount importance to develop mathematical techniques capable of detecting the most relevant parameters, and then address the impact of their variation on the outputs of interest. This requires the solution of many queries to the forward problem. In this context, three classical situations we may face are (i) optimal control and optimal design, (ii) parameter identification and data assimilation, and (iii) uncertainty quantification.
-
(i) Optimal control and optimal design problems. When we pursue a suitable objective via an optimal strategy to be determined, we act on some inputs of the given partial differential equation, the state problem, such as boundary data, physical coefficients, or the shape of the domain itself, and the control variables, so that the solution of the corresponding state problem could meet the prescribed goal. This yields a PDE-constrained optimization problem; its numerical solution usually poses severe computational challenges, as the state problem needs to be solved several times while searching for the optimal control in an iterative way. Exploiting numerical optimization procedures for blood flow simulations is intended to (a) improve the design of prosthetic devices (such as stents, grafts, ventricular assist devices) with the aim of fulfilling a specific target, or (b) customize treatments or surgical procedures, provided that patient-specific information can be acquired. Examples include the optimal placement of electrodes in a defibrillation stage to damp the electrical activity in the myocardium in a desired way when dealing with the therapeutic treatment of cardiac arrhythmias (Nagaiah, Kunisch and Plank Reference Nagaiah, Kunisch and Plank2013b ), the optimization of the shape of a cannula in order to maximize the flow rate through a ventricular assist device (Marsden Reference Marsden2014), and the improvement of the shape of a coronary bypass graft in order to possibly avoid vessel re-occlusion (Lei, Archie and Kleinstreuer Reference Lei, Archie and Kleinstreuer1997, Dur et al. Reference Dur, Coskun, Coskun, Frakes, Kara and Pekkan2011). The first example mentioned above is an optimal control problem, where the control variable is a current source for the monodomain (or bidomain) equation (see Section 7.1), that is, one of its data. The two other examples address a shape optimization or optimal design problem to be solved, the control variable being the shape of the domain where the state problem is set.
-
(ii) Parameter identification and data assimilation. In principle, cardiovascular models necessitate a huge amount of data, for example the patient’s radiological images and measurements. In general, however, some of them may be missing; remember for instance the issue of missing or defective boundary conditions discussed in Section 4.4, or the lack of biological parameters characterizing the tissue properties. For example, it is very hard to estimate the electrical conductivity of the myocardium for electrophysiology models, whereas (pointwise) measurements of the electrical potential – whose mathematical modelling can be characterized by a PDE model requiring electrical conductivities as inputs – can be easier to acquire. By solving inverse/identification problems in cardiovascular modelling, we aim to identify those inputs which are unknown or affected by uncertainty. For that, we rely on suitable quantities which are (a) acquired from measurements, such as displacements, pressures or flow rates, and (b) obtained as the outcome of a numerical simulation, and match these two sets of values. In other words, to identify those input values yielding the acquired measurements, we need to drive the PDE outcome as near as possible to the measured quantity. In general, vastly different inputs may have produced the observed outcome: this is why, instead of finding the most likely input configuration resulting in the observation performed, we instead rely on statistical inversion theory, in order to incorporate all possible information about the unknown inputs we may have prior to the measurement. This requires us to reformulate inverse problems as problems of statistical inference, for example by means of Bayesian statistics. A second issue is data assimilation. This rather generic term encompasses a wide range of techniques exploited to merge measurements and images into the mathematical model in order to improve numerical simulations. Furthermore, a filtering effect induced by the numerical simulation can also be exploited in view of noise reduction in image and measurement acquisition.
-
(iii) Uncertainty quantification and propagation. Confidence in the outcome of a cardiovascular simulation depends directly on the level of accuracy and certainty at which inputs can be determined. In fact, although outcomes are computed from inputs via a deterministic process, input data are often contaminated by experimental noise, or cannot be fully ascertained. Common sources of uncertainty in cardiovascular simulations include (a) boundary conditions, (b) anatomical models, where each geometric model is contaminated by image noise, (c) flow split, since very often there is a lack of clinical data to determine flow distribution to multiple distal branches, and (d) material properties, related to vessel walls or blood (Sankaran and Marsden Reference Sankaran and Marsden2010). Due to uncertainty, computational simulations have to be performed for a set of different parameter configurations and then merged in order to determine how robust simulation outcomes are with respect to variations of uncertain inputs (Sankaran and Marsden Reference Sankaran and Marsden2011). This is indeed strictly related to the task of parametric studies and sensitivity analyses, and can be seen as a forward uncertainty quantification (UQ) problem. Investigating the propagation of input uncertainties via computed outputs means evaluating suitable statistics of the outputs (such as expected values, moments, confidence bands), which are functions of the parameters affected by uncertainty. On the other hand, the solution of optimal control and inverse identification problems also depends on the experimental noise affecting observations and measurements used during the identification process, or the set-up of a desired target. Evaluating uncertainties in this case, providing suitable confidence intervals for the estimated quantities (not simply point estimates) and characterizing the statistical distribution of the unknown parameters are all inverse UQ problems. In this second case, quantifying uncertainties is even more important because an inverse problem is intrinsically ill-posed.
In the following sections we hone our understanding of these three classes of problems, showing relevant examples in cardiovascular modelling.
9 Control and optimization
Solving a PDE-constrained optimization problem consists of reaching a target by acting on a system governed by PDEs. The goal is to act on a state problem
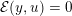 ${\mathcal{E}}(y,u)=0$
given by a PDE system modelling the behaviour of a state variable
${\mathcal{E}}(y,u)=0$
given by a PDE system modelling the behaviour of a state variable
![]() $y$
, through a control variable
$y$
, through a control variable
![]() $u$
in order to reach a desirable target. This is usually done by minimizing (or maximizing) a cost functional
$u$
in order to reach a desirable target. This is usually done by minimizing (or maximizing) a cost functional
 $J=J(y,u)$
expressing some physical index of interest encoding the desired objective – for instance, the squared distance from a target state. For a comprehensive presentation of the functional setting and well-posedness analysis of PDE-constrained optimization, see the monographs by Hinze et al. (Reference Hinze, Pinnau, Ulbrich and Ulbrich2009) and Gunzburger (Reference Gunzburger2003). Other classes of problems of interest in cardiovascular applications, such as those related to parameter estimation, can also be cast in a PDE-constrained optimization framework; see e.g. Section 10.1 for further insights.
$J=J(y,u)$
expressing some physical index of interest encoding the desired objective – for instance, the squared distance from a target state. For a comprehensive presentation of the functional setting and well-posedness analysis of PDE-constrained optimization, see the monographs by Hinze et al. (Reference Hinze, Pinnau, Ulbrich and Ulbrich2009) and Gunzburger (Reference Gunzburger2003). Other classes of problems of interest in cardiovascular applications, such as those related to parameter estimation, can also be cast in a PDE-constrained optimization framework; see e.g. Section 10.1 for further insights.
Generally speaking, a PDE-constrained optimization problem reads
 $$\begin{eqnarray}\min _{y,u}J(y,u)\quad \text{subject to}\quad {\mathcal{E}}(y,u)=0,~~y\in V,~~u\in {\mathcal{U}}_{ad}\subseteq {\mathcal{U}}.\end{eqnarray}$$
$$\begin{eqnarray}\min _{y,u}J(y,u)\quad \text{subject to}\quad {\mathcal{E}}(y,u)=0,~~y\in V,~~u\in {\mathcal{U}}_{ad}\subseteq {\mathcal{U}}.\end{eqnarray}$$
Here
![]() $V$
and
$V$
and
![]() ${\mathcal{U}}$
denote the state and the control space, whereas
${\mathcal{U}}$
denote the state and the control space, whereas
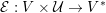 ${\mathcal{E}}:V\times {\mathcal{U}}\rightarrow V^{\ast }$
and
${\mathcal{E}}:V\times {\mathcal{U}}\rightarrow V^{\ast }$
and
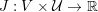 $J:V\times {\mathcal{U}}\rightarrow \mathbb{R}$
denote the state equation and the cost functional, respectively;
$J:V\times {\mathcal{U}}\rightarrow \mathbb{R}$
denote the state equation and the cost functional, respectively;
![]() $V^{\ast }$
is the dual space of
$V^{\ast }$
is the dual space of
![]() $V$
, and
$V$
, and
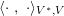 $\langle \cdot ~,~\cdot \rangle _{V^{\ast },V}$
denotes the duality between two elements in
$\langle \cdot ~,~\cdot \rangle _{V^{\ast },V}$
denotes the duality between two elements in
![]() $V^{\ast }$
and
$V^{\ast }$
and
![]() $V$
; similarly,
$V$
; similarly,
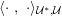 $\langle \cdot ~,~\cdot \rangle _{{\mathcal{U}}^{\ast },{\mathcal{U}}}$
indicates the duality between two elements in
$\langle \cdot ~,~\cdot \rangle _{{\mathcal{U}}^{\ast },{\mathcal{U}}}$
indicates the duality between two elements in
![]() ${\mathcal{U}}^{\ast }$
and
${\mathcal{U}}^{\ast }$
and
![]() ${\mathcal{U}}$
. Additional constraints, depending on the problem at hand, can also be imposed, for example in the form of inequalities; we express this fact by saying that we seek the optimal control in a closed subset
${\mathcal{U}}$
. Additional constraints, depending on the problem at hand, can also be imposed, for example in the form of inequalities; we express this fact by saying that we seek the optimal control in a closed subset
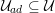 ${\mathcal{U}}_{ad}\subseteq {\mathcal{U}}$
of admissible controls.
${\mathcal{U}}_{ad}\subseteq {\mathcal{U}}$
of admissible controls.
We assume that the state equation
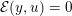 ${\mathcal{E}}(y,u)=0$
has a unique solution
${\mathcal{E}}(y,u)=0$
has a unique solution
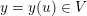 $y=y(u)\in V$
, and that the Fréchet derivative (with respect to
$y=y(u)\in V$
, and that the Fréchet derivative (with respect to
![]() $y$
)
$y$
)
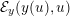 ${\mathcal{E}}_{y}(y(u),u)$
has a bounded inverse for each
${\mathcal{E}}_{y}(y(u),u)$
has a bounded inverse for each
![]() $u\in {\mathcal{U}}$
. Under these assumptions, the solution operator of the state equation is continuously differentiable – we let
$u\in {\mathcal{U}}$
. Under these assumptions, the solution operator of the state equation is continuously differentiable – we let
![]() $y^{\prime }(u)$
denote its derivative – and the reduced formulation
$y^{\prime }(u)$
denote its derivative – and the reduced formulation
 $$\begin{eqnarray}\min _{u}\tilde{J}(u)=J(y(u),u),~~u\in {\mathcal{U}}_{ad}\end{eqnarray}$$
$$\begin{eqnarray}\min _{u}\tilde{J}(u)=J(y(u),u),~~u\in {\mathcal{U}}_{ad}\end{eqnarray}$$
is equivalent to (9.1). Note that this is a convenient framework to embrace – upon defining suitable functional spaces and operators – both stationary and time-dependent state problems; in the following we will make it clear whether the proposed methods can be used to tackle both classes of problems.
9.1 Optimality conditions
The solution
![]() $({\hat{y}},\hat{u} )$
of a PDE-constrained optimization problem such as (9.1) requires a system of optimality conditions to be fulfilled, including the state equation and an optimality condition which involves the gradient of the cost functional. Indeed, if
$({\hat{y}},\hat{u} )$
of a PDE-constrained optimization problem such as (9.1) requires a system of optimality conditions to be fulfilled, including the state equation and an optimality condition which involves the gradient of the cost functional. Indeed, if
![]() $\hat{u} \in U_{ad}$
is a local minimum of
$\hat{u} \in U_{ad}$
is a local minimum of
![]() $\tilde{J}$
, then it satisfies the variational inequality (also referred to as the optimality condition or minimum principle)
$\tilde{J}$
, then it satisfies the variational inequality (also referred to as the optimality condition or minimum principle)
 $$\begin{eqnarray}\langle \tilde{J}^{\prime }(\hat{u} ),v-\hat{u} \rangle _{{\mathcal{U}}^{\ast },{\mathcal{U}}}\geq 0\quad \text{for all}~v\in {\mathcal{U}}_{ad}.\end{eqnarray}$$
$$\begin{eqnarray}\langle \tilde{J}^{\prime }(\hat{u} ),v-\hat{u} \rangle _{{\mathcal{U}}^{\ast },{\mathcal{U}}}\geq 0\quad \text{for all}~v\in {\mathcal{U}}_{ad}.\end{eqnarray}$$
The quantity appearing on the left-hand side is the so-called Gâteaux derivative of
![]() $\tilde{J}$
, evaluated at
$\tilde{J}$
, evaluated at
![]() $\hat{u}$
, in the generic, admissible direction
$\hat{u}$
, in the generic, admissible direction
![]() $v-\hat{u}$
(see e.g. Tröltzsch Reference Tröltzsch2010);
$v-\hat{u}$
(see e.g. Tröltzsch Reference Tröltzsch2010);
![]() $\tilde{J}^{\prime }(\hat{u} )$
denotes the gradient of
$\tilde{J}^{\prime }(\hat{u} )$
denotes the gradient of
![]() $\tilde{J}$
at
$\tilde{J}$
at
![]() $\hat{u}$
. To express this latter quantity in terms of the state solution
$\hat{u}$
. To express this latter quantity in terms of the state solution
![]() $y$
, we can use either (i) the sensitivity approach or (ii) the adjoint approach. As we will see below, in both cases at least a second PDE problem has to be solved in order to evaluate
$y$
, we can use either (i) the sensitivity approach or (ii) the adjoint approach. As we will see below, in both cases at least a second PDE problem has to be solved in order to evaluate
![]() $\tilde{J}^{\prime }(u)$
.
$\tilde{J}^{\prime }(u)$
.
9.1.1 Sensitivity approach
Computing sensitivities requires the evaluation of directional derivatives of both the cost functional and the state solution. For any
 $u,v\in {\mathcal{U}}$
, we can write
$u,v\in {\mathcal{U}}$
, we can write
 $$\begin{eqnarray}\langle \tilde{J}^{\prime }(u),v\rangle _{{\mathcal{U}}^{\ast },{\mathcal{U}}}=\langle J_{y}(y(u),u),y^{\prime }(u)v\rangle _{V^{\ast },V}+\langle J_{u}(y(u),u),v\rangle _{{\mathcal{U}}^{\ast },{\mathcal{U}}}.\end{eqnarray}$$
$$\begin{eqnarray}\langle \tilde{J}^{\prime }(u),v\rangle _{{\mathcal{U}}^{\ast },{\mathcal{U}}}=\langle J_{y}(y(u),u),y^{\prime }(u)v\rangle _{V^{\ast },V}+\langle J_{u}(y(u),u),v\rangle _{{\mathcal{U}}^{\ast },{\mathcal{U}}}.\end{eqnarray}$$
The quantity
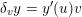 $\unicode[STIX]{x1D6FF}_{v}y=y^{\prime }(u)v$
denotes the sensitivity of the state with respect to the control, evaluated at
$\unicode[STIX]{x1D6FF}_{v}y=y^{\prime }(u)v$
denotes the sensitivity of the state with respect to the control, evaluated at
![]() $u$
, for a given variation
$u$
, for a given variation
![]() $v$
, and can be obtained by solving a further PDE. Indeed, differentiating the state equation
$v$
, and can be obtained by solving a further PDE. Indeed, differentiating the state equation
 ${\mathcal{E}}(y(u),u)=0$
along the direction
${\mathcal{E}}(y(u),u)=0$
along the direction
![]() $v$
, we obtain
$v$
, we obtain
 $$\begin{eqnarray}{\mathcal{E}}_{y}(y(u),u)y^{\prime }(u)v+{\mathcal{E}}_{u}(y(u),u)v=0,\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{E}}_{y}(y(u),u)y^{\prime }(u)v+{\mathcal{E}}_{u}(y(u),u)v=0,\end{eqnarray}$$
where
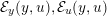 ${\mathcal{E}}_{y}(y,u),{\mathcal{E}}_{u}(y,u)$
are the Fréchet derivatives of the state operator with respect to
${\mathcal{E}}_{y}(y,u),{\mathcal{E}}_{u}(y,u)$
are the Fréchet derivatives of the state operator with respect to
![]() $y$
and
$y$
and
![]() $u$
, respectively; see e.g. Tröltzsch (Reference Tröltzsch2010). Then
$u$
, respectively; see e.g. Tröltzsch (Reference Tröltzsch2010). Then
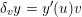 $\unicode[STIX]{x1D6FF}_{v}y=y^{\prime }(u)v$
is given by the solution of the linearized state equation
$\unicode[STIX]{x1D6FF}_{v}y=y^{\prime }(u)v$
is given by the solution of the linearized state equation
 $$\begin{eqnarray}{\mathcal{E}}_{y}(y(u),u)\unicode[STIX]{x1D6FF}_{v}y=-{\mathcal{E}}_{u}(y(u),u)v.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{E}}_{y}(y(u),u)\unicode[STIX]{x1D6FF}_{v}y=-{\mathcal{E}}_{u}(y(u),u)v.\end{eqnarray}$$
Note that
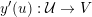 $y^{\prime }(u):{\mathcal{U}}\rightarrow V$
is a linear operator so that, for any admissible
$y^{\prime }(u):{\mathcal{U}}\rightarrow V$
is a linear operator so that, for any admissible
![]() $v\in {\mathcal{U}}$
, a new problem has to be solved to evaluate
$v\in {\mathcal{U}}$
, a new problem has to be solved to evaluate
![]() $\unicode[STIX]{x1D6FF}_{v}y$
. Numerically, this approach is very demanding if the whole gradient
$\unicode[STIX]{x1D6FF}_{v}y$
. Numerically, this approach is very demanding if the whole gradient
![]() $\tilde{J}^{\prime }(u)$
is required: in this case, the number of linearized state equations (9.6) to be solved is equal to the dimension of the control space
$\tilde{J}^{\prime }(u)$
is required: in this case, the number of linearized state equations (9.6) to be solved is equal to the dimension of the control space
![]() ${\mathcal{U}}$
, a task that becomes out of reach as soon as the control has dimension larger than
${\mathcal{U}}$
, a task that becomes out of reach as soon as the control has dimension larger than
![]() $O(10)$
.
$O(10)$
.
9.1.2 Adjoint approach and Lagrange multipliers
A convenient alternative is based on the so-called adjoint approach. By rewriting (9.4) as
 $$\begin{eqnarray}\langle \tilde{J}^{\prime }(u),v\rangle _{{\mathcal{U}}^{\ast },{\mathcal{U}}}=\langle (y^{\prime }(u))^{\ast }J_{y}(y(u),u)+J_{u}(y(u),u),v\rangle _{{\mathcal{U}}^{\ast },{\mathcal{U}}}\end{eqnarray}$$
$$\begin{eqnarray}\langle \tilde{J}^{\prime }(u),v\rangle _{{\mathcal{U}}^{\ast },{\mathcal{U}}}=\langle (y^{\prime }(u))^{\ast }J_{y}(y(u),u)+J_{u}(y(u),u),v\rangle _{{\mathcal{U}}^{\ast },{\mathcal{U}}}\end{eqnarray}$$
and exploiting problem (9.5), we can express the first term on the right-hand side of (9.7) as
 $$\begin{eqnarray}(y^{\prime }(u))^{\ast }J_{y}(y(u),u)=-{\mathcal{E}}_{u}^{\ast }(y(u),u)(({\mathcal{E}}_{y}^{\ast }(y(u),u)))^{-1}J_{y}(y(u),u),\end{eqnarray}$$
$$\begin{eqnarray}(y^{\prime }(u))^{\ast }J_{y}(y(u),u)=-{\mathcal{E}}_{u}^{\ast }(y(u),u)(({\mathcal{E}}_{y}^{\ast }(y(u),u)))^{-1}J_{y}(y(u),u),\end{eqnarray}$$
where
 ${\mathcal{E}}_{u}^{\ast }(y(u),u)$
is the adjoint operatorFootnote
3
of
${\mathcal{E}}_{u}^{\ast }(y(u),u)$
is the adjoint operatorFootnote
3
of
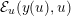 ${\mathcal{E}}_{u}(y(u),u)$
. Let us introduce an additional variable
${\mathcal{E}}_{u}(y(u),u)$
. Let us introduce an additional variable
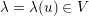 $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}(u)\in V$
, called the adjoint state, the solution of
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}(u)\in V$
, called the adjoint state, the solution of
 $$\begin{eqnarray}{\mathcal{E}}_{y}(y(u),u))^{\ast }\unicode[STIX]{x1D706}=-J_{y}(y(u),u).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{E}}_{y}(y(u),u))^{\ast }\unicode[STIX]{x1D706}=-J_{y}(y(u),u).\end{eqnarray}$$
Then
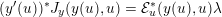 $(y^{\prime }(u))^{\ast }J_{y}(y(u),u)={\mathcal{E}}_{u}^{\ast }(y(u),u)\unicode[STIX]{x1D706}$
; moreover, owing to (9.7), the evaluation of
$(y^{\prime }(u))^{\ast }J_{y}(y(u),u)={\mathcal{E}}_{u}^{\ast }(y(u),u)\unicode[STIX]{x1D706}$
; moreover, owing to (9.7), the evaluation of
 $$\begin{eqnarray}\tilde{J}^{\prime }(u)={\mathcal{E}}_{u}^{\ast }(y(u),u)\unicode[STIX]{x1D706}(u)+J_{u}(y(u),u)\end{eqnarray}$$
$$\begin{eqnarray}\tilde{J}^{\prime }(u)={\mathcal{E}}_{u}^{\ast }(y(u),u)\unicode[STIX]{x1D706}(u)+J_{u}(y(u),u)\end{eqnarray}$$
simply requires us to solve the state problem and a further PDE problem, regardless of the dimension of the control space
![]() ${\mathcal{U}}$
. Note that the adjoint problem is always a linear PDE.
${\mathcal{U}}$
. Note that the adjoint problem is always a linear PDE.
The adjoint-based expression of the gradient of the cost functional (and more generally a system of first-order optimality conditions) can also be obtained, in a more straightforward way, by relying on the Lagrange multiplier method (Hinze et al.
Reference Hinze, Pinnau, Ulbrich and Ulbrich2009). Let us define the Lagrangian functional
 ${\mathcal{L}}:V\times {\mathcal{U}}\times V\rightarrow \mathbb{R}$
,
${\mathcal{L}}:V\times {\mathcal{U}}\times V\rightarrow \mathbb{R}$
,
 $$\begin{eqnarray}{\mathcal{L}}(y,u,\unicode[STIX]{x1D706})=J(y,u)+\langle \unicode[STIX]{x1D706},{\mathcal{E}}(y,u)\rangle _{V,V^{\ast }},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}(y,u,\unicode[STIX]{x1D706})=J(y,u)+\langle \unicode[STIX]{x1D706},{\mathcal{E}}(y,u)\rangle _{V,V^{\ast }},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D706}\in V$
denotes a Lagrange multiplier enforcing the PDE constraint (playing the role of adjoint variable); note that in this case the three variables are independent.
$\unicode[STIX]{x1D706}\in V$
denotes a Lagrange multiplier enforcing the PDE constraint (playing the role of adjoint variable); note that in this case the three variables are independent.
By deriving
![]() ${\mathcal{L}}$
with respect to
${\mathcal{L}}$
with respect to
![]() $\unicode[STIX]{x1D706}$
and imposing that the derivative is equal to zero, we recover the state problem,
$\unicode[STIX]{x1D706}$
and imposing that the derivative is equal to zero, we recover the state problem,
 $$\begin{eqnarray}\langle {\mathcal{L}}_{\unicode[STIX]{x1D706}}(y,u,p),\unicode[STIX]{x1D711}\rangle _{V^{\ast },V}=0\quad \text{for all}~\unicode[STIX]{x1D711}\in V~\Leftrightarrow ~{\mathcal{E}}(y,u)=0.\end{eqnarray}$$
$$\begin{eqnarray}\langle {\mathcal{L}}_{\unicode[STIX]{x1D706}}(y,u,p),\unicode[STIX]{x1D711}\rangle _{V^{\ast },V}=0\quad \text{for all}~\unicode[STIX]{x1D711}\in V~\Leftrightarrow ~{\mathcal{E}}(y,u)=0.\end{eqnarray}$$
Similarly, by deriving
![]() ${\mathcal{L}}$
with respect to
${\mathcal{L}}$
with respect to
![]() $y$
, we obtain the expression of the adjoint problem (9.8),
$y$
, we obtain the expression of the adjoint problem (9.8),
 $$\begin{eqnarray}\langle {\mathcal{L}}_{y}(y,u,p),\unicode[STIX]{x1D713}\rangle _{V^{\ast },V}=0\quad \text{for all}~\unicode[STIX]{x1D713}\in V~\Leftrightarrow ~J_{y}(y,u)+{\mathcal{E}}_{y}^{\ast }(y,u)=0.\end{eqnarray}$$
$$\begin{eqnarray}\langle {\mathcal{L}}_{y}(y,u,p),\unicode[STIX]{x1D713}\rangle _{V^{\ast },V}=0\quad \text{for all}~\unicode[STIX]{x1D713}\in V~\Leftrightarrow ~J_{y}(y,u)+{\mathcal{E}}_{y}^{\ast }(y,u)=0.\end{eqnarray}$$
Finally, at the optimum we impose
 $$\begin{eqnarray}\displaystyle & & \displaystyle \langle {\mathcal{L}}_{u}(y,u,\unicode[STIX]{x1D706}),v-u\rangle _{{\mathcal{U}}^{\ast },{\mathcal{U}}}=0\quad \text{for all}~v\in {\mathcal{U}}_{ad}\nonumber\\ \displaystyle & & \displaystyle \qquad \Leftrightarrow ~\langle J_{u}(y,u)+{\mathcal{E}}_{u}(y,u)^{\ast }\unicode[STIX]{x1D706},v-u\rangle _{{\mathcal{U}}^{\ast },{\mathcal{U}}}\geq 0\quad \text{for all}~v\in {\mathcal{U}}_{ad}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \langle {\mathcal{L}}_{u}(y,u,\unicode[STIX]{x1D706}),v-u\rangle _{{\mathcal{U}}^{\ast },{\mathcal{U}}}=0\quad \text{for all}~v\in {\mathcal{U}}_{ad}\nonumber\\ \displaystyle & & \displaystyle \qquad \Leftrightarrow ~\langle J_{u}(y,u)+{\mathcal{E}}_{u}(y,u)^{\ast }\unicode[STIX]{x1D706},v-u\rangle _{{\mathcal{U}}^{\ast },{\mathcal{U}}}\geq 0\quad \text{for all}~v\in {\mathcal{U}}_{ad}.\nonumber\end{eqnarray}$$
In this way, a system of first-order necessary optimality conditions to be fulfilled by the optimal solution
![]() $(y,u)$
and the corresponding adjoint state
$(y,u)$
and the corresponding adjoint state
![]() $\unicode[STIX]{x1D706}$
is given by the following Karush–Kuhn–Tucker (KKT) system:
$\unicode[STIX]{x1D706}$
is given by the following Karush–Kuhn–Tucker (KKT) system:
 $$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{E}}(y,u)=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{E}}(y,u)=0, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{E}}_{y}(y,u)^{\ast }\hat{\unicode[STIX]{x1D706}}=-J_{y}(y,u), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{E}}_{y}(y,u)^{\ast }\hat{\unicode[STIX]{x1D706}}=-J_{y}(y,u), & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \langle J_{u}(y,u)+{\mathcal{E}}_{u}(y,u)^{\ast }\unicode[STIX]{x1D706},v-u\rangle _{{\mathcal{U}}^{\ast },{\mathcal{U}}}\geq 0\quad \text{for all}~v\in {\mathcal{U}}_{ad}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \langle J_{u}(y,u)+{\mathcal{E}}_{u}(y,u)^{\ast }\unicode[STIX]{x1D706},v-u\rangle _{{\mathcal{U}}^{\ast },{\mathcal{U}}}\geq 0\quad \text{for all}~v\in {\mathcal{U}}_{ad}. & \displaystyle\end{eqnarray}$$
 ${\mathcal{U}}_{ad}\equiv {\mathcal{U}}$
, the variational inequality reduces to the equation
${\mathcal{U}}_{ad}\equiv {\mathcal{U}}$
, the variational inequality reduces to the equation  $$\begin{eqnarray}\langle J_{u}(y,u)+{\mathcal{E}}_{u}(y,u)^{\ast }\unicode[STIX]{x1D706},v\rangle _{{\mathcal{U}}^{\ast },{\mathcal{U}}}=0\quad \text{for all}~v\in {\mathcal{U}},\end{eqnarray}$$
$$\begin{eqnarray}\langle J_{u}(y,u)+{\mathcal{E}}_{u}(y,u)^{\ast }\unicode[STIX]{x1D706},v\rangle _{{\mathcal{U}}^{\ast },{\mathcal{U}}}=0\quad \text{for all}~v\in {\mathcal{U}},\end{eqnarray}$$
so (9.11) can be viewed as the Euler–Lagrange system for the Lagrangian functional, that is, the solutions of (9.11) are the stationary points of
![]() ${\mathcal{L}}(\cdot ,\cdot ,\cdot )$
:
${\mathcal{L}}(\cdot ,\cdot ,\cdot )$
:
 $$\begin{eqnarray}\unicode[STIX]{x1D6FB}{\mathcal{L}}(y,u,\unicode[STIX]{x1D706})[w,v,\unicode[STIX]{x1D702}]=0\quad \text{for all}~(\unicode[STIX]{x1D719},v,\unicode[STIX]{x1D713})\in Y\times {\mathcal{U}}\times V.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FB}{\mathcal{L}}(y,u,\unicode[STIX]{x1D706})[w,v,\unicode[STIX]{x1D702}]=0\quad \text{for all}~(\unicode[STIX]{x1D719},v,\unicode[STIX]{x1D713})\in Y\times {\mathcal{U}}\times V.\end{eqnarray}$$
The third inequality of system (9.11) allows us to recover the expression of the gradient
![]() $\tilde{J}^{\prime }(u)$
. Indeed, since
$\tilde{J}^{\prime }(u)$
. Indeed, since
 ${\mathcal{E}}(y(u),u)=0$
, it holds that
${\mathcal{E}}(y(u),u)=0$
, it holds that
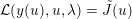 ${\mathcal{L}}(y(u),u,\unicode[STIX]{x1D706})=\tilde{J}(u)$
for any arbitrary
${\mathcal{L}}(y(u),u,\unicode[STIX]{x1D706})=\tilde{J}(u)$
for any arbitrary
![]() $\unicode[STIX]{x1D706}\in V$
, so that, by differentiating this latter equality with respect to
$\unicode[STIX]{x1D706}\in V$
, so that, by differentiating this latter equality with respect to
![]() $u$
, we obtain
$u$
, we obtain
 $$\begin{eqnarray}\displaystyle \langle \tilde{J}^{\prime }(u),v\rangle _{{\mathcal{U}}^{\ast },{\mathcal{U}}} & = & \displaystyle \langle {\mathcal{L}}_{y}(y(u),u,\unicode[STIX]{x1D706}),y^{\prime }(u)v\rangle _{V^{\ast },V}+\langle {\mathcal{L}}_{u}(y(u),u,\unicode[STIX]{x1D706}),v\rangle _{{\mathcal{U}}^{\ast },{\mathcal{U}}}\nonumber\\ \displaystyle & = & \displaystyle \langle {\mathcal{L}}_{u}(y(u),u,\unicode[STIX]{x1D706}),v\rangle _{{\mathcal{U}}^{\ast },{\mathcal{U}}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle \tilde{J}^{\prime }(u),v\rangle _{{\mathcal{U}}^{\ast },{\mathcal{U}}} & = & \displaystyle \langle {\mathcal{L}}_{y}(y(u),u,\unicode[STIX]{x1D706}),y^{\prime }(u)v\rangle _{V^{\ast },V}+\langle {\mathcal{L}}_{u}(y(u),u,\unicode[STIX]{x1D706}),v\rangle _{{\mathcal{U}}^{\ast },{\mathcal{U}}}\nonumber\\ \displaystyle & = & \displaystyle \langle {\mathcal{L}}_{u}(y(u),u,\unicode[STIX]{x1D706}),v\rangle _{{\mathcal{U}}^{\ast },{\mathcal{U}}}.\nonumber\end{eqnarray}$$
Hence,
 $\tilde{J}^{\prime }(u)={\mathcal{L}}_{u}(y(u),u,\unicode[STIX]{x1D706}(u))$
, since
$\tilde{J}^{\prime }(u)={\mathcal{L}}_{u}(y(u),u,\unicode[STIX]{x1D706}(u))$
, since
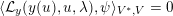 $\langle {\mathcal{L}}_{y}(y(u),u,\unicode[STIX]{x1D706}),\unicode[STIX]{x1D713}\rangle _{V^{\ast },V}=0$
for any
$\langle {\mathcal{L}}_{y}(y(u),u,\unicode[STIX]{x1D706}),\unicode[STIX]{x1D713}\rangle _{V^{\ast },V}=0$
for any
![]() $\unicode[STIX]{x1D713}\in V$
, thanks to (9.10).
$\unicode[STIX]{x1D713}\in V$
, thanks to (9.10).
For illustration we discuss a specific example, by considering the problem of minimizing the energy
 $$\begin{eqnarray}J(\boldsymbol{v},\boldsymbol{u})=\frac{1}{2}\int _{\unicode[STIX]{x1D6FA}_{\mathit{obs}}}|\boldsymbol{v}-\boldsymbol{v}_{d}|^{2}\text{d}\unicode[STIX]{x1D6FA}+\frac{\unicode[STIX]{x1D6FC}}{2}\int _{\unicode[STIX]{x1D6E4}_{\mathit{con}}}|\unicode[STIX]{x1D6FB}\boldsymbol{u}|^{2}\text{d}\unicode[STIX]{x1D6E4},\end{eqnarray}$$
$$\begin{eqnarray}J(\boldsymbol{v},\boldsymbol{u})=\frac{1}{2}\int _{\unicode[STIX]{x1D6FA}_{\mathit{obs}}}|\boldsymbol{v}-\boldsymbol{v}_{d}|^{2}\text{d}\unicode[STIX]{x1D6FA}+\frac{\unicode[STIX]{x1D6FC}}{2}\int _{\unicode[STIX]{x1D6E4}_{\mathit{con}}}|\unicode[STIX]{x1D6FB}\boldsymbol{u}|^{2}\text{d}\unicode[STIX]{x1D6E4},\end{eqnarray}$$
of a fluid flow in a tract of blood vessel where a bypass is inserted. As a matter of fact, the bypass is not simulated. Its action is represented via a velocity control
![]() $\boldsymbol{u}$
acting on the boundary
$\boldsymbol{u}$
acting on the boundary
 $\unicode[STIX]{x1D6E4}_{\mathit{con}}\subset \unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}_{f}$
, the interface where the bypass and the vessel meet: see Figure 9.1. The goal is to regularize the velocity pattern in a suitable observation region
$\unicode[STIX]{x1D6E4}_{\mathit{con}}\subset \unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}_{f}$
, the interface where the bypass and the vessel meet: see Figure 9.1. The goal is to regularize the velocity pattern in a suitable observation region
 $\unicode[STIX]{x1D6FA}_{\mathit{obs}}\subseteq \unicode[STIX]{x1D6FA}_{f}$
by requiring
$\unicode[STIX]{x1D6FA}_{\mathit{obs}}\subseteq \unicode[STIX]{x1D6FA}_{f}$
by requiring
![]() $\boldsymbol{v}$
to be as close as possible to a desired distribution
$\boldsymbol{v}$
to be as close as possible to a desired distribution
![]() $\boldsymbol{v}_{d}$
; see the related discussion in the next section. Referring to the notation in Section 4, for simplicity, we consider a steady version of the Navier–Stokes equations (4.1a
, 4.1b
), for which the velocity/pressure couple
$\boldsymbol{v}_{d}$
; see the related discussion in the next section. Referring to the notation in Section 4, for simplicity, we consider a steady version of the Navier–Stokes equations (4.1a
, 4.1b
), for which the velocity/pressure couple
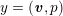 $y=(\boldsymbol{v},p)$
solves the state problem
$y=(\boldsymbol{v},p)$
solves the state problem
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}ll@{}}\displaystyle -\unicode[STIX]{x1D6FB}\cdot \mathbf{T}_{f}(\boldsymbol{v},p)+\unicode[STIX]{x1D70C}_{f}(\boldsymbol{v}\cdot \unicode[STIX]{x1D6FB})\boldsymbol{v}=\mathbf{0} & \quad \text{in }\unicode[STIX]{x1D6FA}_{f},\\ \displaystyle \unicode[STIX]{x1D6FB}\cdot \boldsymbol{v}=0 & \quad \text{in }\unicode[STIX]{x1D6FA}_{f},\\ \displaystyle \boldsymbol{v}=\boldsymbol{ v}_{\mathit{in}} & \quad \text{on }\unicode[STIX]{x1D6E4}_{\mathit{in}},\\ \displaystyle \boldsymbol{v}=\boldsymbol{ 0} & \quad \text{on }\unicode[STIX]{x1D6E4}_{w},\\ \displaystyle \boldsymbol{v}=\boldsymbol{ u} & \quad \text{on }\unicode[STIX]{x1D6E4}_{\mathit{con}},\\ \displaystyle \boldsymbol{T}_{f}(\boldsymbol{v},p)\boldsymbol{n}=\mathbf{0} & \quad \text{on }\unicode[STIX]{x1D6E4}_{\mathit{out}},\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}ll@{}}\displaystyle -\unicode[STIX]{x1D6FB}\cdot \mathbf{T}_{f}(\boldsymbol{v},p)+\unicode[STIX]{x1D70C}_{f}(\boldsymbol{v}\cdot \unicode[STIX]{x1D6FB})\boldsymbol{v}=\mathbf{0} & \quad \text{in }\unicode[STIX]{x1D6FA}_{f},\\ \displaystyle \unicode[STIX]{x1D6FB}\cdot \boldsymbol{v}=0 & \quad \text{in }\unicode[STIX]{x1D6FA}_{f},\\ \displaystyle \boldsymbol{v}=\boldsymbol{ v}_{\mathit{in}} & \quad \text{on }\unicode[STIX]{x1D6E4}_{\mathit{in}},\\ \displaystyle \boldsymbol{v}=\boldsymbol{ 0} & \quad \text{on }\unicode[STIX]{x1D6E4}_{w},\\ \displaystyle \boldsymbol{v}=\boldsymbol{ u} & \quad \text{on }\unicode[STIX]{x1D6E4}_{\mathit{con}},\\ \displaystyle \boldsymbol{T}_{f}(\boldsymbol{v},p)\boldsymbol{n}=\mathbf{0} & \quad \text{on }\unicode[STIX]{x1D6E4}_{\mathit{out}},\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
where the control variable is the velocity
![]() $\boldsymbol{u}$
imposed on the boundary
$\boldsymbol{u}$
imposed on the boundary
![]() $\unicode[STIX]{x1D6E4}_{\mathit{con}}$
. Here
$\unicode[STIX]{x1D6E4}_{\mathit{con}}$
. Here
![]() $\unicode[STIX]{x1D6FC}>0$
is a parameter penalizing the control magnitude (or cost); this can also be seen as a regularization term, ensuring the convexity of the cost functional. The fluid Cauchy stress tensor
$\unicode[STIX]{x1D6FC}>0$
is a parameter penalizing the control magnitude (or cost); this can also be seen as a regularization term, ensuring the convexity of the cost functional. The fluid Cauchy stress tensor
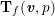 $\mathbf{T}_{f}(\boldsymbol{v},p)$
has been defined in (4.2).
$\mathbf{T}_{f}(\boldsymbol{v},p)$
has been defined in (4.2).

Figure 9.1. (a) Schematic representation of a bypass graft. (b) Domain, boundary portion and observation region for the bypass model problem.
Following the Lagrangian approach, we can derive a system of first-order optimality conditions, where the adjoint problem for the adjoint variables
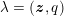 $\unicode[STIX]{x1D706}=(\boldsymbol{z},q)$
is given by
$\unicode[STIX]{x1D706}=(\boldsymbol{z},q)$
is given by
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}ll@{}}-\unicode[STIX]{x1D6FB}\cdot \mathbf{T}_{f}(\boldsymbol{z},q)+\unicode[STIX]{x1D70C}_{f}(\unicode[STIX]{x1D6FB}^{T}\boldsymbol{v})\boldsymbol{z}-\unicode[STIX]{x1D70C}_{f}(\boldsymbol{v}\cdot \unicode[STIX]{x1D6FB})\boldsymbol{z} & \\ \quad =(\boldsymbol{v}-\boldsymbol{v}_{d}){\mathcal{I}}_{\unicode[STIX]{x1D6FA}_{\mathit{obs}}} & \text{in }\unicode[STIX]{x1D6FA}_{f},\\ \unicode[STIX]{x1D6FB}\cdot \boldsymbol{z}=0 & \text{in }\unicode[STIX]{x1D6FA}_{f},\\ \boldsymbol{z}=\mathbf{0} & \text{on }\unicode[STIX]{x1D6E4}_{\mathit{in}}\cup \unicode[STIX]{x1D6E4}_{w}\cup \unicode[STIX]{x1D6E4}_{\mathit{con}},\\ \boldsymbol{T}_{f}(\boldsymbol{z},q)\boldsymbol{n}=\mathbf{0} & \text{on }\unicode[STIX]{x1D6E4}_{\mathit{out}},\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}ll@{}}-\unicode[STIX]{x1D6FB}\cdot \mathbf{T}_{f}(\boldsymbol{z},q)+\unicode[STIX]{x1D70C}_{f}(\unicode[STIX]{x1D6FB}^{T}\boldsymbol{v})\boldsymbol{z}-\unicode[STIX]{x1D70C}_{f}(\boldsymbol{v}\cdot \unicode[STIX]{x1D6FB})\boldsymbol{z} & \\ \quad =(\boldsymbol{v}-\boldsymbol{v}_{d}){\mathcal{I}}_{\unicode[STIX]{x1D6FA}_{\mathit{obs}}} & \text{in }\unicode[STIX]{x1D6FA}_{f},\\ \unicode[STIX]{x1D6FB}\cdot \boldsymbol{z}=0 & \text{in }\unicode[STIX]{x1D6FA}_{f},\\ \boldsymbol{z}=\mathbf{0} & \text{on }\unicode[STIX]{x1D6E4}_{\mathit{in}}\cup \unicode[STIX]{x1D6E4}_{w}\cup \unicode[STIX]{x1D6E4}_{\mathit{con}},\\ \boldsymbol{T}_{f}(\boldsymbol{z},q)\boldsymbol{n}=\mathbf{0} & \text{on }\unicode[STIX]{x1D6E4}_{\mathit{out}},\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
where
 ${\mathcal{I}}_{\unicode[STIX]{x1D6FA}_{\mathit{obs}}}={\mathcal{I}}_{\unicode[STIX]{x1D6FA}_{\mathit{obs}}}(\mathbf{x})$
is the characteristic function of the region
${\mathcal{I}}_{\unicode[STIX]{x1D6FA}_{\mathit{obs}}}={\mathcal{I}}_{\unicode[STIX]{x1D6FA}_{\mathit{obs}}}(\mathbf{x})$
is the characteristic function of the region
![]() $\unicode[STIX]{x1D6FA}_{\mathit{obs}}$
. Note that the adjoint problem is linear in
$\unicode[STIX]{x1D6FA}_{\mathit{obs}}$
. Note that the adjoint problem is linear in
![]() $(\boldsymbol{z},q)$
, and comes from the linearization of the Navier–Stokes equations around the state solution; the optimality condition instead reads
$(\boldsymbol{z},q)$
, and comes from the linearization of the Navier–Stokes equations around the state solution; the optimality condition instead reads
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}\boldsymbol{u}+\boldsymbol{z}=\mathbf{0}\quad \text{on }\unicode[STIX]{x1D6E4}_{\mathit{con}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}\boldsymbol{u}+\boldsymbol{z}=\mathbf{0}\quad \text{on }\unicode[STIX]{x1D6E4}_{\mathit{con}}.\end{eqnarray}$$
Remark 9.1. In the case of time-dependent state problems, the adjoint problem is backward-in-time. Depending on the observation appearing in the cost functional – which can be either on the whole time interval
![]() $(0,T)$
or at the final time
$(0,T)$
or at the final time
![]() $T$
only – the dependence of the adjoint problem on the state is only at
$T$
only – the dependence of the adjoint problem on the state is only at
![]() $t=T$
(thus, as initial condition) or on the whole interval
$t=T$
(thus, as initial condition) or on the whole interval
![]() $(0,T)$
. The approach followed so far can still be employed to derive a system of optimality conditions: see e.g. Section 9.3.2 for further details of a case of interest.
$(0,T)$
. The approach followed so far can still be employed to derive a system of optimality conditions: see e.g. Section 9.3.2 for further details of a case of interest.
9.2 Numerical approximation
Solving a PDE-constrained optimization problem entails a computational effort larger than that required for the solution of a forward (state) problem. The two formulations (9.1) and (9.2) yield two different paradigms for the approximation of such a problem. In the former case, both state and control variables are optimization variables and PDE constraints are explicitly specified; in the latter, only the control variable
![]() $u$
is an optimization variable, whereas the state variable
$u$
is an optimization variable, whereas the state variable
![]() $y$
is considered to be an implicit function of
$y$
is considered to be an implicit function of
![]() $u$
via the PDE constraint.Footnote
4
In this latter case, the solution of the state problem is nested in the evaluation of the gradient
$u$
via the PDE constraint.Footnote
4
In this latter case, the solution of the state problem is nested in the evaluation of the gradient
![]() $\tilde{J}^{\prime }(u)$
of the reduced cost functional.
$\tilde{J}^{\prime }(u)$
of the reduced cost functional.
Algorithms for solving PDE-constrained optimization problems can be sorted according to several criteria. An initial classification criterion is between iterative methods, rooted in iterative minimization algorithms for the reduced cost functional, and all-at-once methods, where the PDE constraint is kept explicitly and the three equations forming (9.11) are solved simultaneously. Another criterion is concerned with the highest order of derivatives exploited by the algorithm, yielding derivative-free methods, gradient-based methods and Hessian-based methods.
A different perspective is taken when addressing the interplay between optimization and discretization: numerical discretization can be performed before or after the derivation of a system of optimality conditions. More precisely, in the so-called optimize-then-discretize approach, optimization is carried out at the continuous level (e.g. to find system (9.11)) and then the discretization is operated on the resulting optimality system. Alternatively, using the discretize-then-optimize approach, we first approximate the state equation (and the cost functional) and then carry out the optimization at the discrete level. Here we address the former approach; further details are given at the end of this section. For brevity, we recall the main features of iterative and all-at-once methods in the case of unconstrained problems, that is, problems without further equality/inequality constraints or, equivalently, for which
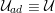 ${\mathcal{U}}_{ad}\equiv {\mathcal{U}}$
. In particular,
${\mathcal{U}}_{ad}\equiv {\mathcal{U}}$
. In particular,
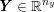 $\boldsymbol{Y}\in \mathbb{R}^{n_{y}}$
,
$\boldsymbol{Y}\in \mathbb{R}^{n_{y}}$
,
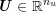 $\boldsymbol{U}\in \mathbb{R}^{n_{u}}$
denote the discrete representation of the state and the control variable, respectively, whereas
$\boldsymbol{U}\in \mathbb{R}^{n_{u}}$
denote the discrete representation of the state and the control variable, respectively, whereas
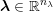 $\boldsymbol{\unicode[STIX]{x1D706}}\in \mathbb{R}^{n_{\unicode[STIX]{x1D706}}}$
is the discrete adjoint variable.
$\boldsymbol{\unicode[STIX]{x1D706}}\in \mathbb{R}^{n_{\unicode[STIX]{x1D706}}}$
is the discrete adjoint variable.
9.2.1 Iterative methods
Iterative (also referred to as black-box) methods treat the reduced problem
 $$\begin{eqnarray}\min _{\boldsymbol{U}}\tilde{J}(\boldsymbol{U})=J(\boldsymbol{Y}(\boldsymbol{U}),\boldsymbol{U}),\end{eqnarray}$$
$$\begin{eqnarray}\min _{\boldsymbol{U}}\tilde{J}(\boldsymbol{U})=J(\boldsymbol{Y}(\boldsymbol{U}),\boldsymbol{U}),\end{eqnarray}$$
once
![]() $\boldsymbol{U}$
is known;
$\boldsymbol{U}$
is known;
![]() $\boldsymbol{Y}(\boldsymbol{U})$
is obtained as the solution of the state equation. An existing algorithm for the solution of the state equation therefore has to be embedded into an optimization loop, and any available PDE and optimization routines can be freely combined. In particular, iterative methods are a popular choice when dealing with optimal control problems by extending an existing code for the state problem. Within this class, a notable difference exists between gradient-based and non-gradient-based algorithms.
$\boldsymbol{Y}(\boldsymbol{U})$
is obtained as the solution of the state equation. An existing algorithm for the solution of the state equation therefore has to be embedded into an optimization loop, and any available PDE and optimization routines can be freely combined. In particular, iterative methods are a popular choice when dealing with optimal control problems by extending an existing code for the state problem. Within this class, a notable difference exists between gradient-based and non-gradient-based algorithms.
Non-gradient-based (or derivative-free) algorithms, such as the popular Nelder–Mead algorithm, exploit either comparisons between function evaluations in different directions at each step, or low-order local approximants of
![]() $\tilde{J}$
, in order to assess its local behaviour and find the minimizer: see e.g. Marsden, Feinstein and Taylor (Reference Marsden, Feinstein and Taylor2008). Employing a finite difference approximation of the gradient is an attractive alternative due to its ease of implementation, but it may suffer from limited accuracy and large costs in the presence of many design variables. Hence, these methods are feasible only in the case where the control space has very small dimension, for example if the control is expressed in terms of a vector of
$\tilde{J}$
, in order to assess its local behaviour and find the minimizer: see e.g. Marsden, Feinstein and Taylor (Reference Marsden, Feinstein and Taylor2008). Employing a finite difference approximation of the gradient is an attractive alternative due to its ease of implementation, but it may suffer from limited accuracy and large costs in the presence of many design variables. Hence, these methods are feasible only in the case where the control space has very small dimension, for example if the control is expressed in terms of a vector of
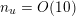 $n_{u}=O(10)$
design variables.
$n_{u}=O(10)$
design variables.
Gradient-based algorithms exploit the gradient
![]() $\tilde{J}^{\prime }$
to iteratively update the control until a suitable convergence criterion is fulfilled. Notable instances are descent methods, such as the gradient, (non-linear) conjugate gradient, quasi-Newton or Newton methods. In the simplest case of a gradient method, starting from an initial guess
$\tilde{J}^{\prime }$
to iteratively update the control until a suitable convergence criterion is fulfilled. Notable instances are descent methods, such as the gradient, (non-linear) conjugate gradient, quasi-Newton or Newton methods. In the simplest case of a gradient method, starting from an initial guess
![]() $\boldsymbol{U}^{(0)}$
we iteratively generate a sequence
$\boldsymbol{U}^{(0)}$
we iteratively generate a sequence
 $$\begin{eqnarray}\boldsymbol{U}^{(k+1)}=\boldsymbol{U}^{(k)}-\unicode[STIX]{x1D70F}_{k}\tilde{J}^{\prime }(\boldsymbol{U}^{(k)}),\quad k=0,1,\ldots ,\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{U}^{(k+1)}=\boldsymbol{U}^{(k)}-\unicode[STIX]{x1D70F}_{k}\tilde{J}^{\prime }(\boldsymbol{U}^{(k)}),\quad k=0,1,\ldots ,\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D70F}_{k}>0$
is a step size, until e.g.
$\unicode[STIX]{x1D70F}_{k}>0$
is a step size, until e.g.
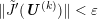 $\Vert \tilde{J}^{\prime }(\boldsymbol{U}^{(k)})\Vert <\unicode[STIX]{x1D700}$
, for a given tolerance
$\Vert \tilde{J}^{\prime }(\boldsymbol{U}^{(k)})\Vert <\unicode[STIX]{x1D700}$
, for a given tolerance
![]() $\unicode[STIX]{x1D700}>0$
. Further details can be found in Nocedal (Reference Nocedal1992) and Kelley (Reference Kelley1999), for example. The solver for the state equation has to be augmented with a routine which provides the gradient of the state with respect to the optimization variables, and hence the solution of the adjoint problem. Optimization algorithms with faster convergence rates are needed to speed up the execution of the whole algorithm. Although straightforward to implement, the gradient method suffers from a poor rate of convergence when dealing with the numerical solutions of PDE-constrained optimization problems. More efficient methods are more typically employed, such as quasi-Newton methods: see e.g. Borzì and Schulz (Reference Borzì and Schulz2011) for further details.
$\unicode[STIX]{x1D700}>0$
. Further details can be found in Nocedal (Reference Nocedal1992) and Kelley (Reference Kelley1999), for example. The solver for the state equation has to be augmented with a routine which provides the gradient of the state with respect to the optimization variables, and hence the solution of the adjoint problem. Optimization algorithms with faster convergence rates are needed to speed up the execution of the whole algorithm. Although straightforward to implement, the gradient method suffers from a poor rate of convergence when dealing with the numerical solutions of PDE-constrained optimization problems. More efficient methods are more typically employed, such as quasi-Newton methods: see e.g. Borzì and Schulz (Reference Borzì and Schulz2011) for further details.
9.2.2 All-at-once methods
By treating both the control and the state variables as independent optimization variables, coupled via the PDE constraint, we deal with an equality constrained non-linear optimization problem, the state equation now playing the role of equality constraint. The goal of all-at-once (also referred to as one-shot) methods is to tackle the (possibly) non-linear optimality system (9.11) as a whole problem to be solved. After numerical discretization, in the unconstrained case we obtain the algebraic system
 $$\begin{eqnarray}\displaystyle & \displaystyle J_{\boldsymbol{Y}}(\boldsymbol{Y},\boldsymbol{U})+\mathbf{e}_{\boldsymbol{Y}}^{T}(\boldsymbol{Y},\boldsymbol{U})\boldsymbol{\unicode[STIX]{x1D706}}=\mathbf{0}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle J_{\boldsymbol{Y}}(\boldsymbol{Y},\boldsymbol{U})+\mathbf{e}_{\boldsymbol{Y}}^{T}(\boldsymbol{Y},\boldsymbol{U})\boldsymbol{\unicode[STIX]{x1D706}}=\mathbf{0}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle J_{\boldsymbol{U}}(\boldsymbol{Y},\boldsymbol{U})+\mathbf{e}_{\boldsymbol{U}}^{T}(\boldsymbol{Y},\boldsymbol{U})\boldsymbol{\unicode[STIX]{x1D706}}=\mathbf{0}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle J_{\boldsymbol{U}}(\boldsymbol{Y},\boldsymbol{U})+\mathbf{e}_{\boldsymbol{U}}^{T}(\boldsymbol{Y},\boldsymbol{U})\boldsymbol{\unicode[STIX]{x1D706}}=\mathbf{0}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \mathbf{e}(\boldsymbol{Y},\boldsymbol{U})=\mathbf{0}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \mathbf{e}(\boldsymbol{Y},\boldsymbol{U})=\mathbf{0}. & \displaystyle\end{eqnarray}$$
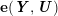 $\mathbf{e}(\boldsymbol{Y},\boldsymbol{U})$
denotes the discrete state operator,
$\mathbf{e}(\boldsymbol{Y},\boldsymbol{U})$
denotes the discrete state operator,
 ${\mathcal{L}}(\boldsymbol{Y},\boldsymbol{U},\boldsymbol{\unicode[STIX]{x1D706}})=J(\boldsymbol{Y},\boldsymbol{U})-\boldsymbol{\unicode[STIX]{x1D706}}^{T}\mathbf{e}(\boldsymbol{Y},\boldsymbol{U})$
vanishes.
${\mathcal{L}}(\boldsymbol{Y},\boldsymbol{U},\boldsymbol{\unicode[STIX]{x1D706}})=J(\boldsymbol{Y},\boldsymbol{U})-\boldsymbol{\unicode[STIX]{x1D706}}^{T}\mathbf{e}(\boldsymbol{Y},\boldsymbol{U})$
vanishes.
The strategy above is well suited to PDE-constrained optimization problems involving stationary state systems, but it is more computationally involved in the time-dependent case. If
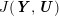 $J(\boldsymbol{Y},\boldsymbol{U})$
is quadratic and
$J(\boldsymbol{Y},\boldsymbol{U})$
is quadratic and
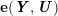 $\mathbf{e}(\boldsymbol{Y},\boldsymbol{U})$
is linear in
$\mathbf{e}(\boldsymbol{Y},\boldsymbol{U})$
is linear in
![]() $\boldsymbol{Y}$
and
$\boldsymbol{Y}$
and
![]() $\boldsymbol{U}$
, (9.12) is a linear system of equations in saddle-point form, such as those arising from quadratic programming. In this case, preconditioned iterative methods for linear systems could be employed, such as those based on Krylov subspaces. In this respect, several preconditioners have been proposed in the past decade, in which multigrid schemes are exploited as inner solvers (or preconditioners) for some blocks of the KKT matrix within an outer iterative solver; see e.g. Benzi et al. (Reference Benzi, Golub and Liesen2005) and Rees, Dollar and Wathen (Reference Rees, Dollar and Wathen2010). More recent extensions to constrained problems have been addressed, for example in Borzì and Schulz (Reference Borzì and Schulz2011) and the references therein.
$\boldsymbol{U}$
, (9.12) is a linear system of equations in saddle-point form, such as those arising from quadratic programming. In this case, preconditioned iterative methods for linear systems could be employed, such as those based on Krylov subspaces. In this respect, several preconditioners have been proposed in the past decade, in which multigrid schemes are exploited as inner solvers (or preconditioners) for some blocks of the KKT matrix within an outer iterative solver; see e.g. Benzi et al. (Reference Benzi, Golub and Liesen2005) and Rees, Dollar and Wathen (Reference Rees, Dollar and Wathen2010). More recent extensions to constrained problems have been addressed, for example in Borzì and Schulz (Reference Borzì and Schulz2011) and the references therein.
If the state problem is non-linear, the optimality system has to be solved via appropriate linearization procedures (e.g. sequential quadratic programming methods) or modern penalty methods (e.g. augmented Lagrangian methods). Indeed, the equations of system (9.12) are still linear in
![]() $\boldsymbol{\unicode[STIX]{x1D706}}$
but non-linear in
$\boldsymbol{\unicode[STIX]{x1D706}}$
but non-linear in
![]() $(\boldsymbol{Y},\boldsymbol{U})$
. When a Newton-type method is applied to (9.12), each iteration on the KKT system entails the solution of the linear system
$(\boldsymbol{Y},\boldsymbol{U})$
. When a Newton-type method is applied to (9.12), each iteration on the KKT system entails the solution of the linear system
 $$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}{\mathcal{L}}_{\boldsymbol{Y}\boldsymbol{Y}} & {\mathcal{L}}_{\boldsymbol{Y}\boldsymbol{U}} & \mathbf{e}_{\boldsymbol{Y}}^{T}\\ {\mathcal{L}}_{\boldsymbol{U}\boldsymbol{Y}} & {\mathcal{L}}_{\boldsymbol{U}\boldsymbol{U}} & \mathbf{e}_{\boldsymbol{U}}^{T}\\ \boldsymbol{ e}_{\boldsymbol{Y}} & \mathbf{e}_{\boldsymbol{U}} & 0\end{array}\right)\left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D6FF}\boldsymbol{Y}\\ \unicode[STIX]{x1D6FF}\boldsymbol{U}\\ \boldsymbol{\unicode[STIX]{x1D706}}^{(k+1)}\end{array}\right)=-\left(\begin{array}{@{}c@{}}J_{\boldsymbol{Y}}\\ J_{\boldsymbol{U}}\\ \mathbf{e}\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}{\mathcal{L}}_{\boldsymbol{Y}\boldsymbol{Y}} & {\mathcal{L}}_{\boldsymbol{Y}\boldsymbol{U}} & \mathbf{e}_{\boldsymbol{Y}}^{T}\\ {\mathcal{L}}_{\boldsymbol{U}\boldsymbol{Y}} & {\mathcal{L}}_{\boldsymbol{U}\boldsymbol{U}} & \mathbf{e}_{\boldsymbol{U}}^{T}\\ \boldsymbol{ e}_{\boldsymbol{Y}} & \mathbf{e}_{\boldsymbol{U}} & 0\end{array}\right)\left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D6FF}\boldsymbol{Y}\\ \unicode[STIX]{x1D6FF}\boldsymbol{U}\\ \boldsymbol{\unicode[STIX]{x1D706}}^{(k+1)}\end{array}\right)=-\left(\begin{array}{@{}c@{}}J_{\boldsymbol{Y}}\\ J_{\boldsymbol{U}}\\ \mathbf{e}\end{array}\right)\end{eqnarray}$$
for the update
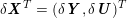 $\unicode[STIX]{x1D6FF}\boldsymbol{X}^{T}=(\unicode[STIX]{x1D6FF}\boldsymbol{Y},\unicode[STIX]{x1D6FF}\boldsymbol{U})^{T}$
of the optimization variable and the new value
$\unicode[STIX]{x1D6FF}\boldsymbol{X}^{T}=(\unicode[STIX]{x1D6FF}\boldsymbol{Y},\unicode[STIX]{x1D6FF}\boldsymbol{U})^{T}$
of the optimization variable and the new value
![]() $\boldsymbol{\unicode[STIX]{x1D706}}^{(k+1)}$
of the adjoint variable. Then we set
$\boldsymbol{\unicode[STIX]{x1D706}}^{(k+1)}$
of the adjoint variable. Then we set
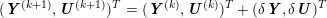 $(\boldsymbol{Y}^{(k+1)},\boldsymbol{U}^{(k+1)})^{T}=(\boldsymbol{Y}^{(k)},\boldsymbol{U}^{(k)})^{T}+(\unicode[STIX]{x1D6FF}\boldsymbol{Y},\unicode[STIX]{x1D6FF}\boldsymbol{U})^{T}$
. Here
$(\boldsymbol{Y}^{(k+1)},\boldsymbol{U}^{(k+1)})^{T}=(\boldsymbol{Y}^{(k)},\boldsymbol{U}^{(k)})^{T}+(\unicode[STIX]{x1D6FF}\boldsymbol{Y},\unicode[STIX]{x1D6FF}\boldsymbol{U})^{T}$
. Here
 $$\begin{eqnarray}{\mathcal{H}}=\left(\begin{array}{@{}cc@{}}{\mathcal{L}}_{\boldsymbol{Y}\boldsymbol{Y}} & {\mathcal{L}}_{\boldsymbol{Y}\boldsymbol{U}}\\ {\mathcal{L}}_{\boldsymbol{U}\boldsymbol{Y}} & {\mathcal{L}}_{\boldsymbol{U}\boldsymbol{U}}\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}=\left(\begin{array}{@{}cc@{}}{\mathcal{L}}_{\boldsymbol{Y}\boldsymbol{Y}} & {\mathcal{L}}_{\boldsymbol{Y}\boldsymbol{U}}\\ {\mathcal{L}}_{\boldsymbol{U}\boldsymbol{Y}} & {\mathcal{L}}_{\boldsymbol{U}\boldsymbol{U}}\end{array}\right)\end{eqnarray}$$
denotes the Hessian of the Lagrangian functional, to be evaluated at
 $(\boldsymbol{Y}^{(k)},\boldsymbol{U}^{(k)},\boldsymbol{\unicode[STIX]{x1D706}}^{(k)})^{T}$
. Note the saddle-point structure of system (9.13), where the adjoint variable indeed plays the role of multiplier for the constraint expressed by the (linearized) state equation. The system (9.13) can be equivalently obtained as the KKT system for the linear-quadratic optimization problem
$(\boldsymbol{Y}^{(k)},\boldsymbol{U}^{(k)},\boldsymbol{\unicode[STIX]{x1D706}}^{(k)})^{T}$
. Note the saddle-point structure of system (9.13), where the adjoint variable indeed plays the role of multiplier for the constraint expressed by the (linearized) state equation. The system (9.13) can be equivalently obtained as the KKT system for the linear-quadratic optimization problem
 $$\begin{eqnarray}\min _{\unicode[STIX]{x1D6FF}\boldsymbol{X}}\biggl[\frac{1}{2}\unicode[STIX]{x1D6FF}\boldsymbol{X}^{T}{\mathcal{H}}\unicode[STIX]{x1D6FF}\boldsymbol{X}+\left(\begin{array}{@{}c@{}}J_{\boldsymbol{Y}}\\ J_{\boldsymbol{U}}\end{array}\right)^{T}\unicode[STIX]{x1D6FF}\boldsymbol{X}\biggr]\quad \text{subject to}\quad \left(\begin{array}{@{}c@{}}\mathbf{e}_{\boldsymbol{Y}}\\ \boldsymbol{ e}_{\boldsymbol{U}}\end{array}\right)\unicode[STIX]{x1D6FF}\boldsymbol{ X}+\mathbf{e}=0\end{eqnarray}$$
$$\begin{eqnarray}\min _{\unicode[STIX]{x1D6FF}\boldsymbol{X}}\biggl[\frac{1}{2}\unicode[STIX]{x1D6FF}\boldsymbol{X}^{T}{\mathcal{H}}\unicode[STIX]{x1D6FF}\boldsymbol{X}+\left(\begin{array}{@{}c@{}}J_{\boldsymbol{Y}}\\ J_{\boldsymbol{U}}\end{array}\right)^{T}\unicode[STIX]{x1D6FF}\boldsymbol{X}\biggr]\quad \text{subject to}\quad \left(\begin{array}{@{}c@{}}\mathbf{e}_{\boldsymbol{Y}}\\ \boldsymbol{ e}_{\boldsymbol{U}}\end{array}\right)\unicode[STIX]{x1D6FF}\boldsymbol{ X}+\mathbf{e}=0\end{eqnarray}$$
(e.g. Hinze et al. Reference Hinze, Pinnau, Ulbrich and Ulbrich2009, Borzì and Schulz Reference Borzì and Schulz2011), whence the name sequential quadratic programming method, which is commonly used to refer to the Newton iterations on system (9.13). Indeed, a quadratic programming problem has to be solved at each step, for example by means of a preconditioned Krylov method such as MINRES, until a suitable convergence criterion is fulfilled. Suitable approximations of the Hessian, based for example on quasi-Newton methods, are required to make this algorithm more computationally attractive: see e.g. Borzì and Schulz (Reference Borzì and Schulz2011).
Remark 9.2. Constraints on the control and/or state variables add non-linearity to the optimization problem. A first option is to treat inequality constraints in an outer loop, via penalty methods which allow us to convert them into additional terms in the cost functional. For instance, if
![]() $u\leq b$
is a pointwise control constraint, the term
$u\leq b$
is a pointwise control constraint, the term
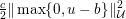 ${\textstyle \frac{c}{2}}\Vert \max \{0,u-b\}\Vert _{{\mathcal{U}}}^{2}$
can be added, where
${\textstyle \frac{c}{2}}\Vert \max \{0,u-b\}\Vert _{{\mathcal{U}}}^{2}$
can be added, where
![]() $c>0$
is a penalty parameter to be properly selected, and then an iterative method can be used in the inner loop. Another option in iterative methods is to perform a projection over the space of admissible controls at each step. More efficient strategies to tackle constrained problems are usually obtained when dealing with constraints in the main optimization loop, such as in the case of primal–dual active set strategies: see e.g. the monographs by Borzì and Schulz (Reference Borzì and Schulz2011) and Hinze et al. (Reference Hinze, Pinnau, Ulbrich and Ulbrich2009).
$c>0$
is a penalty parameter to be properly selected, and then an iterative method can be used in the inner loop. Another option in iterative methods is to perform a projection over the space of admissible controls at each step. More efficient strategies to tackle constrained problems are usually obtained when dealing with constraints in the main optimization loop, such as in the case of primal–dual active set strategies: see e.g. the monographs by Borzì and Schulz (Reference Borzì and Schulz2011) and Hinze et al. (Reference Hinze, Pinnau, Ulbrich and Ulbrich2009).
We finally point out that in this section we have opted for the optimize-then-discretize approach: that is, we have shown how to recover a system of optimality conditions and then proceed to its numerical discretization. The opposite strategy (discretize-then-optimize) would have led to substantially similar numerical methods, by choosing either an iterative or an all-at-once method for the system of optimality conditions derived once the original state system had been discretized. The two approaches do not generally yield identical solutions; see e.g. Hinze et al. (Reference Hinze, Pinnau, Ulbrich and Ulbrich2009) for a discussion.
9.3 Applications to cardiovascular modelling
9.3.1 Optimal design of bypass grafts
PDE-constrained optimization problems are obtained when looking for the optimal design of prosthetic devices, such as ventricular assist devices or bypass grafts. For instance, coronary artery bypass grafting (CABG) is a standard surgical procedure to restore blood perfusion to the cardiac muscle by redirecting blood from the aorta through a graft vessel downstream of a coronary artery affected by stenosis or occlusion. The ability to design the graft-vessel connection (the so-called anastomosis, which we refer to as the domain
![]() $\unicode[STIX]{x1D6FA}$
) in an efficient way is a potentially critical factor in preventing post-operative recurrence of re-stenosis.
$\unicode[STIX]{x1D6FA}$
) in an efficient way is a potentially critical factor in preventing post-operative recurrence of re-stenosis.
Today it is accepted that intimal wall thickening, caused by the accelerated growth of smooth muscle cells and the surrounding matrix, is one of the leading causes of long-term failure of end-to-side vascular grafts (Haruguchi and Teraoka Reference Haruguchi and Teraoka2003). Low and/or highly oscillatory patterns of wall shear stress (WSS), as well as strong vorticity and recirculations, cause intimal wall thickening (Ethier et al.
Reference Ethier, Steinman, Zhang, Karpik and Ojha1998, Keynton et al.
Reference Keynton, Evancho, Sims, Rodway, Gobin and Rittgers2001) at sites where curvatures, bifurcations, tortuosity and branching occur, and, more generally, where flow departs from unidirectional patterns (Giordana et al.
Reference Giordana, Sherwin, Peiró, Doorly, Crane, Lee, Cheshire and Caro2005, Loth, Fischer and Bassiouny Reference Loth, Fischer and Bassiouny2008). In mathematical terms, an optimal graft is one that minimizes suitable cost functionals involving the area of low WSS, the spatial WSS gradient (Lei et al.
Reference Lei, Archie and Kleinstreuer1997) or the vorticity (Quarteroni and Rozza Reference Quarteroni and Rozza2003, Manzoni, Quarteroni and Rozza Reference Manzoni, Quarteroni and Rozza2012b
); see e.g. Kleinstreuer (Reference Kleinstreuer2006) for a detailed review. Taking blood velocity
![]() $\mathbf{v}$
and pressure
$\mathbf{v}$
and pressure
![]() $p$
as state variables, and
$p$
as state variables, and
![]() $u=\unicode[STIX]{x1D6FA}$
(i.e. the shape of the domain itself) as the control variable, the goal is thus to find the optimal shape
$u=\unicode[STIX]{x1D6FA}$
(i.e. the shape of the domain itself) as the control variable, the goal is thus to find the optimal shape
![]() $\hat{\unicode[STIX]{x1D6FA}}$
of the graft by minimizing the cost functional
$\hat{\unicode[STIX]{x1D6FA}}$
of the graft by minimizing the cost functional
 $$\begin{eqnarray}J(\boldsymbol{v},\unicode[STIX]{x1D6FA})=\int _{0}^{T}\int _{\unicode[STIX]{x1D6FA}_{\mathit{obs}}}|\unicode[STIX]{x1D6FB}\times \boldsymbol{v}|^{2}\text{d}\unicode[STIX]{x1D714}\text{d}t,\end{eqnarray}$$
$$\begin{eqnarray}J(\boldsymbol{v},\unicode[STIX]{x1D6FA})=\int _{0}^{T}\int _{\unicode[STIX]{x1D6FA}_{\mathit{obs}}}|\unicode[STIX]{x1D6FB}\times \boldsymbol{v}|^{2}\text{d}\unicode[STIX]{x1D714}\text{d}t,\end{eqnarray}$$
where
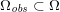 $\unicode[STIX]{x1D6FA}_{\mathit{obs}}\subset \unicode[STIX]{x1D6FA}$
is a given observation region in the artery portion immediately after the anastomosis. Indeed, high downstream vorticity may lead to strong flow recirculation, yielding similar effects in terms of intimal thickening.
$\unicode[STIX]{x1D6FA}_{\mathit{obs}}\subset \unicode[STIX]{x1D6FA}$
is a given observation region in the artery portion immediately after the anastomosis. Indeed, high downstream vorticity may lead to strong flow recirculation, yielding similar effects in terms of intimal thickening.
Other cost functionals that can be employed include the following.
-
∙ A tracking-type functional, in order to drive the blood velocity (and pressure, if
 $\unicode[STIX]{x1D6FF}>0$
) towards a specified velocity (and pressure) target state
$\unicode[STIX]{x1D6FF}>0$
) towards a specified velocity (and pressure) target state
 $\boldsymbol{v}_{d}$
,
$\boldsymbol{v}_{d}$
,
 $p_{d}$
, featuring a regular pattern: A typical choice of
$p_{d}$
, featuring a regular pattern: A typical choice of $$\begin{eqnarray}J(\boldsymbol{v},\unicode[STIX]{x1D6FA})=\frac{1}{2}\int _{0}^{T}\int _{\unicode[STIX]{x1D6FA}_{\mathit{obs}}}|\boldsymbol{v}-\boldsymbol{v}_{d}|^{2}\text{d}\unicode[STIX]{x1D6FA}\text{d}t+\frac{\unicode[STIX]{x1D6FF}}{2}\int _{0}^{T}\int _{\unicode[STIX]{x1D6FA}_{\mathit{obs}}}|p-p_{d}|^{2}\text{d}\unicode[STIX]{x1D714}\text{d}t.\end{eqnarray}$$
$$\begin{eqnarray}J(\boldsymbol{v},\unicode[STIX]{x1D6FA})=\frac{1}{2}\int _{0}^{T}\int _{\unicode[STIX]{x1D6FA}_{\mathit{obs}}}|\boldsymbol{v}-\boldsymbol{v}_{d}|^{2}\text{d}\unicode[STIX]{x1D6FA}\text{d}t+\frac{\unicode[STIX]{x1D6FF}}{2}\int _{0}^{T}\int _{\unicode[STIX]{x1D6FA}_{\mathit{obs}}}|p-p_{d}|^{2}\text{d}\unicode[STIX]{x1D714}\text{d}t.\end{eqnarray}$$
 $(\boldsymbol{v}_{d},p_{d})$
is provided by the Stokes (or a low-Reynolds Navier–Stokes) flow in the same domain.
$(\boldsymbol{v}_{d},p_{d})$
is provided by the Stokes (or a low-Reynolds Navier–Stokes) flow in the same domain.
-
∙ In two dimensions, a Galilean invariant vortex measure identifies a region as a vortex if
 $\unicode[STIX]{x1D6FB}\boldsymbol{v}$
has complex eigenvalues, that is, if
$\unicode[STIX]{x1D6FB}\boldsymbol{v}$
has complex eigenvalues, that is, if
 $\det (\unicode[STIX]{x1D6FB}\boldsymbol{v})>0$
. Following Hintermüller et al. (Reference Hintermüller, Kunisch, Spasov and Volkwein2004), Kunisch and Vexler (Reference Kunisch and Vexler2007) and Lassila et al. (Reference Lassila, Manzoni, Quarteroni and Rozza2013a
), then can be used when dealing with vortex suppression.
$\det (\unicode[STIX]{x1D6FB}\boldsymbol{v})>0$
. Following Hintermüller et al. (Reference Hintermüller, Kunisch, Spasov and Volkwein2004), Kunisch and Vexler (Reference Kunisch and Vexler2007) and Lassila et al. (Reference Lassila, Manzoni, Quarteroni and Rozza2013a
), then can be used when dealing with vortex suppression. $$\begin{eqnarray}J(\boldsymbol{v},\unicode[STIX]{x1D6FA})=\int _{0}^{T}\int _{\unicode[STIX]{x1D6FA}_{\mathit{obs}}}\max (0,\det (\unicode[STIX]{x1D6FB}\boldsymbol{v}))\text{d}\unicode[STIX]{x1D714}\text{d}t\end{eqnarray}$$
$$\begin{eqnarray}J(\boldsymbol{v},\unicode[STIX]{x1D6FA})=\int _{0}^{T}\int _{\unicode[STIX]{x1D6FA}_{\mathit{obs}}}\max (0,\det (\unicode[STIX]{x1D6FB}\boldsymbol{v}))\text{d}\unicode[STIX]{x1D714}\text{d}t\end{eqnarray}$$
-
∙ A WSS gradient-based functional is given by
that is, by a time-averaged WSS gradient, measured over the portion $$\begin{eqnarray}\displaystyle J(\boldsymbol{v},\unicode[STIX]{x1D6FA}) & = & \displaystyle \int _{0}^{T}\int _{\unicode[STIX]{x1D6E4}_{\mathit{obs}}}\mathit{WSSG}(t)\text{d}\unicode[STIX]{x1D6FE}\text{d}t,\nonumber\\ \displaystyle \mathit{WSSG}(t) & = & \displaystyle \biggl(\biggl(\frac{\unicode[STIX]{x2202}\boldsymbol{w}_{p}}{\unicode[STIX]{x2202}\boldsymbol{\unicode[STIX]{x1D70F}}_{p}}\biggr)^{2}+\biggl(\frac{\unicode[STIX]{x2202}\boldsymbol{w}_{n}}{\unicode[STIX]{x2202}\boldsymbol{\unicode[STIX]{x1D70F}}_{n}}\biggr)^{2}\biggr),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J(\boldsymbol{v},\unicode[STIX]{x1D6FA}) & = & \displaystyle \int _{0}^{T}\int _{\unicode[STIX]{x1D6E4}_{\mathit{obs}}}\mathit{WSSG}(t)\text{d}\unicode[STIX]{x1D6FE}\text{d}t,\nonumber\\ \displaystyle \mathit{WSSG}(t) & = & \displaystyle \biggl(\biggl(\frac{\unicode[STIX]{x2202}\boldsymbol{w}_{p}}{\unicode[STIX]{x2202}\boldsymbol{\unicode[STIX]{x1D70F}}_{p}}\biggr)^{2}+\biggl(\frac{\unicode[STIX]{x2202}\boldsymbol{w}_{n}}{\unicode[STIX]{x2202}\boldsymbol{\unicode[STIX]{x1D70F}}_{n}}\biggr)^{2}\biggr),\nonumber\end{eqnarray}$$
 $\unicode[STIX]{x1D6E4}_{\mathit{obs}}\subset \unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
of the boundary in the anastomosis region. Here,
$\unicode[STIX]{x1D6E4}_{\mathit{obs}}\subset \unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
of the boundary in the anastomosis region. Here,
 $\mathit{WSSG}$
denotes the WSS gradient, where
$\mathit{WSSG}$
denotes the WSS gradient, where
 $\boldsymbol{w}=\boldsymbol{w}(t,\boldsymbol{x})$
is the WSS vector of components
$\boldsymbol{w}=\boldsymbol{w}(t,\boldsymbol{x})$
is the WSS vector of components
 $w^{(j)}=\unicode[STIX]{x1D707}\unicode[STIX]{x1D6FB}\boldsymbol{v}\boldsymbol{n}(t,\boldsymbol{x})\cdot \boldsymbol{\unicode[STIX]{x1D70F}}^{(j)}$
, and
$w^{(j)}=\unicode[STIX]{x1D707}\unicode[STIX]{x1D6FB}\boldsymbol{v}\boldsymbol{n}(t,\boldsymbol{x})\cdot \boldsymbol{\unicode[STIX]{x1D70F}}^{(j)}$
, and
 $\boldsymbol{\unicode[STIX]{x1D70F}}_{p}$
and
$\boldsymbol{\unicode[STIX]{x1D70F}}_{p}$
and
 $\boldsymbol{\unicode[STIX]{x1D70F}}_{n}$
are the unit vectors parallel and normal to the direction of the time-averaged WSS vector
$\boldsymbol{\unicode[STIX]{x1D70F}}_{n}$
are the unit vectors parallel and normal to the direction of the time-averaged WSS vector
 $\boldsymbol{w}$
, respectively. Only a linear combination of the normal components
$\boldsymbol{w}$
, respectively. Only a linear combination of the normal components
 $\unicode[STIX]{x2202}\boldsymbol{x}_{j}/\unicode[STIX]{x2202}\boldsymbol{\unicode[STIX]{x1D70F}}_{j}$
,
$\unicode[STIX]{x2202}\boldsymbol{x}_{j}/\unicode[STIX]{x2202}\boldsymbol{\unicode[STIX]{x1D70F}}_{j}$
,
 $j=p,n$
is considered as an index to quantify the tension yielding intimal thickening. Moreover, the time-averaged WSS is relatively insensitive to changes in the anastomosis configuration, whereas the time-averaged WSS gradient is highly sensitive, and has been linked to localized mechanobiological responses in tissues (see Lei et al. Reference Lei, Archie and Kleinstreuer1997 and the discussion therein). Using
$j=p,n$
is considered as an index to quantify the tension yielding intimal thickening. Moreover, the time-averaged WSS is relatively insensitive to changes in the anastomosis configuration, whereas the time-averaged WSS gradient is highly sensitive, and has been linked to localized mechanobiological responses in tissues (see Lei et al. Reference Lei, Archie and Kleinstreuer1997 and the discussion therein). Using
 $\mathit{WSSG}$
rather than
$\mathit{WSSG}$
rather than
 $\mathit{WSS}$
can be understood as filtering the WSS by removing its component induced by the steady mean flow and considering only the spatially fluctuating term as part of the indicator. For the sake of numerical efficiency of the whole optimization process, a steady flow simulation (e.g. corresponding to the systolic peak) can be considered, and the WSS gradient of the steady flow can be taken as an approximation of the time-averaged WSS gradient. The interested reader can refer to Kleinstreuer (Reference Kleinstreuer2006), for example, for further details.
$\mathit{WSS}$
can be understood as filtering the WSS by removing its component induced by the steady mean flow and considering only the spatially fluctuating term as part of the indicator. For the sake of numerical efficiency of the whole optimization process, a steady flow simulation (e.g. corresponding to the systolic peak) can be considered, and the WSS gradient of the steady flow can be taken as an approximation of the time-averaged WSS gradient. The interested reader can refer to Kleinstreuer (Reference Kleinstreuer2006), for example, for further details.
Many works of the past few decades have focused on the optimal shape design of end-to-side anastomoses, typically by acting on the wall shape near the anastomosis by local shape variation. If a simpler parametric optimization approach is considered, the three most significant design variables (see Loth et al. Reference Loth, Fischer and Bassiouny2008) are the anastomosis angle, the graft-to-host diameter ratio (Keynton et al. Reference Keynton, Evancho, Sims, Rodway, Gobin and Rittgers2001, Do et al. Reference Do, Owida, Yang and Morsi2011) and the toe shape, that is, the profile of the bypass junction. Optimizing a complex configuration in terms of few design variables is more advantageous since it is known that grafts usually have an extended patch or cuff that effectively provides a hood to ease the flow transition from the graft to the artery. Further, improved anastomosis design must comply with the constraints set by surgical realization. For a more comprehensive review of bypass graft design results, we refer to Migliavacca and Dubini (Reference Migliavacca and Dubini2005), Loth et al. (Reference Loth, Fischer and Bassiouny2008), Owida, Do and Morsi (Reference Owida, Do and Morsi2012) and Marsden (Reference Marsden2014).
Concerning the objective to be minimized, each cost functional involves suitable observations, obtained as functions of the state variables over the entire domain or some boundary portions, and over a given time interval and, possibly, data acquired from measurements, as in the case of a tracking-type functional. There are of course other parameters affecting the cost functional, such as the Reynolds number, or the flow split between the proximal host artery and the graft, i.e. the ratio of the corresponding flow rates (Giordana et al. Reference Giordana, Sherwin, Peiró, Doorly, Crane, Lee, Cheshire and Caro2005). All these parameters should be considered as uncertainties within a robust optimization framework, in order to characterize the optimal shape of the graft in a range of possible operating conditions. Examples of optimal design in the presence of uncertainty in cardiovascular applications have been considered by Sankaran and Marsden (Reference Sankaran and Marsden2010).
As a concluding remark, we point out that the coupling of optimization algorithms to blood flow simulations is computationally challenging, since each evaluation of the cost functional requires the solution of an unsteady, three-dimensional Navier–Stokes problem. If relying on the adjoint approach to characterize the gradient of the cost functional, a further linearized Navier–Stokes (Oseen) problem has to be solved at every iteration. For this reason, the majority of works related to applications in surgery and device optimization have focused, so far, on small-scale and/or two-dimensional problems, or on steady-flow problems, usually relying on gradient-free methods.
For the sake of illustration, we report some numerical results for the optimal design of a femoropopliteal bypass graft. This surgery is used to bypass diseased blood vessels above or below the knee, and is one of the most common surgical treatments of chronic lower-extremity ischaemia. We model the blood flow across a bypass graft via a steady Navier–Stokes model, and consider a vorticity cost functional
 $$\begin{eqnarray}J(\boldsymbol{v},\unicode[STIX]{x1D6FA})=\int _{\unicode[STIX]{x1D6FA}_{\mathit{obs}}}|\unicode[STIX]{x1D6FB}\times \boldsymbol{v}|^{2}\text{d}\unicode[STIX]{x1D714},\end{eqnarray}$$
$$\begin{eqnarray}J(\boldsymbol{v},\unicode[STIX]{x1D6FA})=\int _{\unicode[STIX]{x1D6FA}_{\mathit{obs}}}|\unicode[STIX]{x1D6FB}\times \boldsymbol{v}|^{2}\text{d}\unicode[STIX]{x1D714},\end{eqnarray}$$
where
 $\unicode[STIX]{x1D6FA}_{\mathit{obs}}\subset \unicode[STIX]{x1D6FA}$
is the observation region. Initial and optimal shapes are shown in Figure 9.2 for the case of a stenosed host artery; its occlusion, either total or partial, is expressed via a Dirichlet boundary condition on the incoming velocity field on
$\unicode[STIX]{x1D6FA}_{\mathit{obs}}\subset \unicode[STIX]{x1D6FA}$
is the observation region. Initial and optimal shapes are shown in Figure 9.2 for the case of a stenosed host artery; its occlusion, either total or partial, is expressed via a Dirichlet boundary condition on the incoming velocity field on
![]() $\unicode[STIX]{x1D6E4}_{\mathit{res}}$
, homogeneous for the completely occluded case and non-homogeneous otherwise. See Figure 9.2(b) for the definition of
$\unicode[STIX]{x1D6E4}_{\mathit{res}}$
, homogeneous for the completely occluded case and non-homogeneous otherwise. See Figure 9.2(b) for the definition of
![]() $\unicode[STIX]{x1D6FA}_{\mathit{obs}}$
and
$\unicode[STIX]{x1D6FA}_{\mathit{obs}}$
and
![]() $\unicode[STIX]{x1D6E4}_{\mathit{ref}}$
. A shape parametrization technique based on free-form deformations (FFDs) is very suitable for describing admissible shapes via deformation of a reference configuration by acting on a small set of control points: see e.g. Manzoni (Reference Manzoni2012) and Manzoni et al. (Reference Manzoni, Quarteroni and Rozza2012b
).
$\unicode[STIX]{x1D6E4}_{\mathit{ref}}$
. A shape parametrization technique based on free-form deformations (FFDs) is very suitable for describing admissible shapes via deformation of a reference configuration by acting on a small set of control points: see e.g. Manzoni (Reference Manzoni2012) and Manzoni et al. (Reference Manzoni, Quarteroni and Rozza2012b
).

Figure 9.2. Optimal design of bypass grafts. (a) A tract of femoral artery with a bypass graft. (b) Computational domain, boundaries and observation region; (c) FFD shape parametrization used to generate admissible shapes. Global shape deformations are induced by the displacement of a few selected control points (shown in red) in the
![]() $6\times 4$
FFD lattice. These control points are selected by a preliminary screening procedure based on sensitivity analysis. (d) Initial and (e) optimal bypass configurations in the case of total (above) or partial (below) occlusion. Numerical results were obtained using the MATLAB finite element library MLife.
$6\times 4$
FFD lattice. These control points are selected by a preliminary screening procedure based on sensitivity analysis. (d) Initial and (e) optimal bypass configurations in the case of total (above) or partial (below) occlusion. Numerical results were obtained using the MATLAB finite element library MLife.
9.3.2 Optimal control of electrical defibrillation
Whereas in healthy conditions the electrical activation of the heart is an extremely organized (and efficient) process, some disturbances in the formation and/or propagation of electrical signals may induce re-entrant activation patterns which lead to tachycardia, that is, a noticeable increase in the heart’s activation rate. In the worst cases, this may turn into an even less organized activation pattern, called fibrillation. A common therapy to terminate fibrillation and restore regular cardiac rhythm is electrical defibrillation, consisting in the delivery of a strong electrical shock by injecting external currents through a set of electrodes. This restores a spatially uniform activation pattern, recovering an extracellular potential distribution showing damped voltage gradients. Today, electrical defibrillation is carried out by implanting devices (so-called cardioverter defibrillators) able to monitor the heart rhythm and then deliver electrical discharges when needed.
This process can be modelled by considering the monodomain equation (7.11) as the state system, for which the extracellular stimulation current
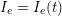 $I_{e}=I_{e}(t)$
to be applied plays the role of a distributed control function, and has to be determined in order to minimize the cost functional
$I_{e}=I_{e}(t)$
to be applied plays the role of a distributed control function, and has to be determined in order to minimize the cost functional
 $$\begin{eqnarray}J(V_{m},I_{e})=\frac{1}{2}\int _{0}^{T}\int _{\unicode[STIX]{x1D6FA}_{\mathit{obs}}}|V_{m}-v_{d}|^{2}\text{d}\unicode[STIX]{x1D6FA}\text{d}t+\frac{\unicode[STIX]{x1D6FC}}{2}\int _{0}^{T}\int _{\unicode[STIX]{x1D6FA}_{\mathit{con}}}|I_{e}|^{2}\text{d}\unicode[STIX]{x1D6FA}\text{d}t.\end{eqnarray}$$
$$\begin{eqnarray}J(V_{m},I_{e})=\frac{1}{2}\int _{0}^{T}\int _{\unicode[STIX]{x1D6FA}_{\mathit{obs}}}|V_{m}-v_{d}|^{2}\text{d}\unicode[STIX]{x1D6FA}\text{d}t+\frac{\unicode[STIX]{x1D6FC}}{2}\int _{0}^{T}\int _{\unicode[STIX]{x1D6FA}_{\mathit{con}}}|I_{e}|^{2}\text{d}\unicode[STIX]{x1D6FA}\text{d}t.\end{eqnarray}$$
Here
![]() $V_{m}$
is the trans-membrane potential,
$V_{m}$
is the trans-membrane potential,
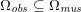 $\unicode[STIX]{x1D6FA}_{\mathit{obs}}\subseteq \unicode[STIX]{x1D6FA}_{\mathit{mus}}$
is the observation domain,
$\unicode[STIX]{x1D6FA}_{\mathit{obs}}\subseteq \unicode[STIX]{x1D6FA}_{\mathit{mus}}$
is the observation domain,
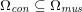 $\unicode[STIX]{x1D6FA}_{\mathit{con}}\subseteq \unicode[STIX]{x1D6FA}_{\mathit{mus}}$
is the control domain, and
$\unicode[STIX]{x1D6FA}_{\mathit{con}}\subseteq \unicode[STIX]{x1D6FA}_{\mathit{mus}}$
is the control domain, and
![]() $v_{d}$
is the target potential distribution. For instance, if
$v_{d}$
is the target potential distribution. For instance, if
![]() $v_{d}=0$
, the minimum of
$v_{d}=0$
, the minimum of
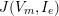 $J(V_{m},I_{e})$
corresponds to the case of an excitation wave which is suppressed in the region
$J(V_{m},I_{e})$
corresponds to the case of an excitation wave which is suppressed in the region
![]() $\unicode[STIX]{x1D6FA}_{\mathit{obs}}$
: see e.g. Nagaiah, Kunisch and Plank (Reference Nagaiah, Kunisch and Plank2011). The trans-membrane potential
$\unicode[STIX]{x1D6FA}_{\mathit{obs}}$
: see e.g. Nagaiah, Kunisch and Plank (Reference Nagaiah, Kunisch and Plank2011). The trans-membrane potential
![]() $V_{m}$
can be obtained by solving the monodomain equations
$V_{m}$
can be obtained by solving the monodomain equations
 $$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D712}_{m}C_{m}\frac{\unicode[STIX]{x2202}V_{m}}{\unicode[STIX]{x2202}t}-\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{\unicode[STIX]{x1D6F4}}\unicode[STIX]{x1D6FB}V_{m})+\unicode[STIX]{x1D712}_{m}I_{\mathit{ion}}=I_{e}\quad & & \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}\times (0,T),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D712}_{m}C_{m}\frac{\unicode[STIX]{x2202}V_{m}}{\unicode[STIX]{x2202}t}-\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{\unicode[STIX]{x1D6F4}}\unicode[STIX]{x1D6FB}V_{m})+\unicode[STIX]{x1D712}_{m}I_{\mathit{ion}}=I_{e}\quad & & \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}\times (0,T),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}t}=g(V_{m},w)\quad & & \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}\times (0,T),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}t}=g(V_{m},w)\quad & & \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}\times (0,T),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle V_{m}|_{t=0}=V_{m,0}\quad & & \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle V_{m}|_{t=0}=V_{m,0}\quad & & \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle w|_{t=0}=w_{0}\quad & & \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle w|_{t=0}=w_{0}\quad & & \displaystyle \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{\unicode[STIX]{x1D6F4}}\unicode[STIX]{x1D6FB}V_{m}\cdot \mathbf{n}=0\quad & & \displaystyle \text{on }\unicode[STIX]{x1D6F4}_{\mathit{epi}}\cup \unicode[STIX]{x1D6F4}_{\mathit{endo}}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{\unicode[STIX]{x1D6F4}}\unicode[STIX]{x1D6FB}V_{m}\cdot \mathbf{n}=0\quad & & \displaystyle \text{on }\unicode[STIX]{x1D6F4}_{\mathit{epi}}\cup \unicode[STIX]{x1D6F4}_{\mathit{endo}}\end{eqnarray}$$
 $$\begin{eqnarray}I_{\mathit{ion}}=f(V_{m},w)=-kV_{m}(V_{m}-a)(V_{m}-1)-w,\quad g(V_{m},w)=\unicode[STIX]{x1D716}(V_{m}-\unicode[STIX]{x1D6FE}w).\end{eqnarray}$$
$$\begin{eqnarray}I_{\mathit{ion}}=f(V_{m},w)=-kV_{m}(V_{m}-a)(V_{m}-1)-w,\quad g(V_{m},w)=\unicode[STIX]{x1D716}(V_{m}-\unicode[STIX]{x1D6FE}w).\end{eqnarray}$$
An analysis of this optimal control problem can be found in Nagaiah et al. (Reference Nagaiah, Kunisch and Plank2011), for example. We can exploit the Lagrangian approach to derive a system of first-order optimality conditions, by introducing the Lagrangian
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle {\mathcal{L}}(V_{m},w,I_{e},z,q)\nonumber\\ \displaystyle & & \displaystyle \displaystyle \qquad =J(V_{m},I_{e})+\langle {\mathcal{E}}(V_{m},w,I_{e}),(z,q)\rangle _{V,V^{\ast }}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \qquad =J(V_{m},I_{e})\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad \qquad +\,\int _{0}^{T}\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\biggl(\unicode[STIX]{x1D712}_{m}C_{m}\frac{\unicode[STIX]{x2202}V_{m}}{\unicode[STIX]{x2202}t}-\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{\unicode[STIX]{x1D6F4}}\unicode[STIX]{x1D6FB}V_{m})+\unicode[STIX]{x1D712}_{m}I_{\mathit{ion}}-I_{e}\biggr)z\text{d}\unicode[STIX]{x1D6FA}\text{d}t\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad \qquad +\,\int _{0}^{T}\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\biggl(\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}t}-g(V_{m},w)\biggr)q\text{d}\unicode[STIX]{x1D6FA}\text{d}t,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle {\mathcal{L}}(V_{m},w,I_{e},z,q)\nonumber\\ \displaystyle & & \displaystyle \displaystyle \qquad =J(V_{m},I_{e})+\langle {\mathcal{E}}(V_{m},w,I_{e}),(z,q)\rangle _{V,V^{\ast }}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \qquad =J(V_{m},I_{e})\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad \qquad +\,\int _{0}^{T}\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\biggl(\unicode[STIX]{x1D712}_{m}C_{m}\frac{\unicode[STIX]{x2202}V_{m}}{\unicode[STIX]{x2202}t}-\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{\unicode[STIX]{x1D6F4}}\unicode[STIX]{x1D6FB}V_{m})+\unicode[STIX]{x1D712}_{m}I_{\mathit{ion}}-I_{e}\biggr)z\text{d}\unicode[STIX]{x1D6FA}\text{d}t\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad \qquad +\,\int _{0}^{T}\int _{\unicode[STIX]{x1D6FA}_{\mathit{mus}}}\biggl(\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}t}-g(V_{m},w)\biggr)q\text{d}\unicode[STIX]{x1D6FA}\text{d}t,\nonumber\end{eqnarray}$$
where
![]() $(z,q)$
denote the dual variables of
$(z,q)$
denote the dual variables of
![]() $V_{m}$
,
$V_{m}$
,
![]() $w$
, respectively. Here
$w$
, respectively. Here
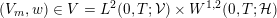 $(V_{m},w)\in V=L^{2}(0,T;{\mathcal{V}})\times W^{1,2}(0,T;{\mathcal{H}})$
, where
$(V_{m},w)\in V=L^{2}(0,T;{\mathcal{V}})\times W^{1,2}(0,T;{\mathcal{H}})$
, where
 ${\mathcal{V}}=H^{1}(\unicode[STIX]{x1D6FA}_{\mathit{mus}})$
and
${\mathcal{V}}=H^{1}(\unicode[STIX]{x1D6FA}_{\mathit{mus}})$
and
 ${\mathcal{H}}=L^{2}(\unicode[STIX]{x1D6FA}_{\mathit{mus}})$
; the control space can be chosen as
${\mathcal{H}}=L^{2}(\unicode[STIX]{x1D6FA}_{\mathit{mus}})$
; the control space can be chosen as
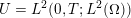 $U=L^{2}(0,T;L^{2}(\unicode[STIX]{x1D6FA}))$
, and the initial conditions can be kept as explicit constraints. By setting the partial derivatives of
$U=L^{2}(0,T;L^{2}(\unicode[STIX]{x1D6FA}))$
, and the initial conditions can be kept as explicit constraints. By setting the partial derivatives of
![]() ${\mathcal{L}}$
equal to zero, we find the following expression for the adjoint problem:
${\mathcal{L}}$
equal to zero, we find the following expression for the adjoint problem:
 $$\begin{eqnarray}\displaystyle \displaystyle -\unicode[STIX]{x1D712}_{m}C_{m}\frac{\unicode[STIX]{x2202}z}{\unicode[STIX]{x2202}t}-\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{\unicode[STIX]{x1D6F4}}\unicode[STIX]{x1D6FB}z)+\unicode[STIX]{x1D712}_{m}\frac{\unicode[STIX]{x2202}I_{\mathit{ion}}}{\unicode[STIX]{x2202}V_{m}}z-\frac{\unicode[STIX]{x2202}g}{\unicode[STIX]{x2202}V_{m}}q & & \displaystyle \nonumber\\ \displaystyle \displaystyle \quad =v_{d}-V_{m} & & \displaystyle \quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}\times (0,T),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle -\unicode[STIX]{x1D712}_{m}C_{m}\frac{\unicode[STIX]{x2202}z}{\unicode[STIX]{x2202}t}-\unicode[STIX]{x1D6FB}\cdot (\boldsymbol{\unicode[STIX]{x1D6F4}}\unicode[STIX]{x1D6FB}z)+\unicode[STIX]{x1D712}_{m}\frac{\unicode[STIX]{x2202}I_{\mathit{ion}}}{\unicode[STIX]{x2202}V_{m}}z-\frac{\unicode[STIX]{x2202}g}{\unicode[STIX]{x2202}V_{m}}q & & \displaystyle \nonumber\\ \displaystyle \displaystyle \quad =v_{d}-V_{m} & & \displaystyle \quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}\times (0,T),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle -\frac{\unicode[STIX]{x2202}q}{\unicode[STIX]{x2202}t}-\frac{\unicode[STIX]{x2202}g}{\unicode[STIX]{x2202}w}q+\frac{\unicode[STIX]{x2202}I_{\mathit{ion}}}{\unicode[STIX]{x2202}w}z=0 & & \displaystyle \quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}\times (0,T),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle -\frac{\unicode[STIX]{x2202}q}{\unicode[STIX]{x2202}t}-\frac{\unicode[STIX]{x2202}g}{\unicode[STIX]{x2202}w}q+\frac{\unicode[STIX]{x2202}I_{\mathit{ion}}}{\unicode[STIX]{x2202}w}z=0 & & \displaystyle \quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}}\times (0,T),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle z|_{t=T}=0 & & \displaystyle \quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle z|_{t=T}=0 & & \displaystyle \quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle q|_{t=T}=0 & & \displaystyle \quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle q|_{t=T}=0 & & \displaystyle \quad \text{in }\unicode[STIX]{x1D6FA}_{\mathit{mus}},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{\unicode[STIX]{x1D6F4}}\unicode[STIX]{x1D6FB}z\cdot \mathbf{n}=0 & & \displaystyle \quad \text{on }\unicode[STIX]{x1D6F4}_{\mathit{epi}}\cup \unicode[STIX]{x1D6F4}_{\mathit{endo}}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{\unicode[STIX]{x1D6F4}}\unicode[STIX]{x1D6FB}z\cdot \mathbf{n}=0 & & \displaystyle \quad \text{on }\unicode[STIX]{x1D6F4}_{\mathit{epi}}\cup \unicode[STIX]{x1D6F4}_{\mathit{endo}}\end{eqnarray}$$
 $$\begin{eqnarray}z+\unicode[STIX]{x1D6FC}I_{e}=0\quad \text{on }\unicode[STIX]{x1D6FA}_{\mathit{con}}.\end{eqnarray}$$
$$\begin{eqnarray}z+\unicode[STIX]{x1D6FC}I_{e}=0\quad \text{on }\unicode[STIX]{x1D6FA}_{\mathit{con}}.\end{eqnarray}$$
The optimal control problem (9.14, 9.15) can be solved by an optimize-then-discretize strategy, where both spatial and temporal discretizations are required because of the time-dependent nature of the problem. After discretization, we can employ an iterative method, by computing at each step the solution of the (coupled) state problem (9.15) over
![]() $(0,T)$
, and the solution of the adjoint problem (9.16), which is a linear problem, backward in time, where the adjoint variables are coupled similarly to
$(0,T)$
, and the solution of the adjoint problem (9.16), which is a linear problem, backward in time, where the adjoint variables are coupled similarly to
![]() $(V_{m},w)$
in the state problem. Note that the data of the adjoint problem are related to the Fréchet derivative of the cost functional with respect to the state variables, and that the adjoint problem depends on the control function only through the state variable. Moreover, the adjoint operator calls into play the linearization of the state operator around the computed state solution; that is, the derivatives
$(V_{m},w)$
in the state problem. Note that the data of the adjoint problem are related to the Fréchet derivative of the cost functional with respect to the state variables, and that the adjoint problem depends on the control function only through the state variable. Moreover, the adjoint operator calls into play the linearization of the state operator around the computed state solution; that is, the derivatives
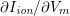 $\unicode[STIX]{x2202}I_{\mathit{ion}}/\unicode[STIX]{x2202}V_{m}$
,
$\unicode[STIX]{x2202}I_{\mathit{ion}}/\unicode[STIX]{x2202}V_{m}$
,
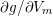 $\unicode[STIX]{x2202}g/\unicode[STIX]{x2202}V_{m}$
,
$\unicode[STIX]{x2202}g/\unicode[STIX]{x2202}V_{m}$
,
 $\unicode[STIX]{x2202}I_{\mathit{ion}}/\unicode[STIX]{x2202}w$
,
$\unicode[STIX]{x2202}I_{\mathit{ion}}/\unicode[STIX]{x2202}w$
,
![]() $\unicode[STIX]{x2202}g/\unicode[STIX]{x2202}w$
have to be evaluated, at each step, around the computed solution of the state system. The optimality condition (9.17) then allows us to determine the gradient
$\unicode[STIX]{x2202}g/\unicode[STIX]{x2202}w$
have to be evaluated, at each step, around the computed solution of the state system. The optimality condition (9.17) then allows us to determine the gradient
![]() $\tilde{J}^{\prime }(I_{e})$
of the cost functional
$\tilde{J}^{\prime }(I_{e})$
of the cost functional
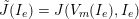 $\tilde{J}(I_{e})=J(V_{m}(I_{e}),I_{e})$
, required to update the control function at each step.
$\tilde{J}(I_{e})=J(V_{m}(I_{e}),I_{e})$
, required to update the control function at each step.
To simplify the optimal control problem, we can for instance look for control functions of the form
 $$\begin{eqnarray}I_{e}(t,\mathbf{x})=\mathop{\sum }_{k=1}^{N_{el}}u_{k}(t){\mathcal{I}}_{\unicode[STIX]{x1D6FA}_{\mathit{con},k}}(\mathbf{x}){\mathcal{I}}_{(0,T_{\mathit{def}})}(t),\end{eqnarray}$$
$$\begin{eqnarray}I_{e}(t,\mathbf{x})=\mathop{\sum }_{k=1}^{N_{el}}u_{k}(t){\mathcal{I}}_{\unicode[STIX]{x1D6FA}_{\mathit{con},k}}(\mathbf{x}){\mathcal{I}}_{(0,T_{\mathit{def}})}(t),\end{eqnarray}$$
where the location of
![]() $N_{el}$
electrodes through which the current is delivered is prescribed, and only its time intensity has to be controlled over time. Here
$N_{el}$
electrodes through which the current is delivered is prescribed, and only its time intensity has to be controlled over time. Here
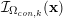 ${\mathcal{I}}_{\unicode[STIX]{x1D6FA}_{\mathit{con},k}}(\mathbf{x})$
denotes the indicator function of the region
${\mathcal{I}}_{\unicode[STIX]{x1D6FA}_{\mathit{con},k}}(\mathbf{x})$
denotes the indicator function of the region
![]() $\unicode[STIX]{x1D6FA}_{\mathit{con},k}$
where the
$\unicode[STIX]{x1D6FA}_{\mathit{con},k}$
where the
![]() $k$
th electrode is located. Additional inequality constraints of the form
$k$
th electrode is located. Additional inequality constraints of the form
 $u_{\min }\leq u_{k}(t)\leq u_{\max }$
can also be taken into account in order to limit current amplitude.
$u_{\min }\leq u_{k}(t)\leq u_{\max }$
can also be taken into account in order to limit current amplitude.
Further extensions of this framework consider, for example, the bidomain model (Nagaiah et al.
Reference Nagaiah, Kunisch and Plank2013b
), the case of boundary controls (Nagaiah, Kunisch and Plank Reference Nagaiah, Kunisch and Plank2013a
), and a different Mitchell–Schaeffer model to describe ionic currents, together with the presence of a conductive bath medium outside the heart effects and experimentally based fibre and sheet orientations (Nagaiah, Kunisch and Plank Reference Nagaiah, Kunisch and Plank2016). Moreover, the case where the shock duration itself is also optimized has been considered by Kunisch and Rund (Reference Kunisch and Rund2015). The reason to consider this further effect is that after applying a defibrillation shock, the muscle tissue needs a suitable amount of time to reach a non-fibrillatory state, so that a successful defibrillation can only be assessed at a time
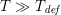 $T\gg T_{\mathit{def}}$
, where
$T\gg T_{\mathit{def}}$
, where
![]() $T_{\mathit{def}}$
is the end time of the defibrillation shock and
$T_{\mathit{def}}$
is the end time of the defibrillation shock and
![]() $T$
the final observation time, at which the tissue should have reached a non-excited state. In this context, the cost functional
$T$
the final observation time, at which the tissue should have reached a non-excited state. In this context, the cost functional
 $$\begin{eqnarray}J(V_{m},u,T_{\mathit{def}})=T_{\mathit{def}}+\frac{\unicode[STIX]{x1D707}}{2}\int _{\unicode[STIX]{x1D6FA}_{\mathit{obs}}}|V_{m}(\cdot ,T)|^{2}\text{d}\unicode[STIX]{x1D6FA}+\frac{\unicode[STIX]{x1D6FC}}{2}\mathop{\sum }_{k=1}^{N_{el}}\int _{0}^{T}|u_{k}|^{2}\text{d}t\end{eqnarray}$$
$$\begin{eqnarray}J(V_{m},u,T_{\mathit{def}})=T_{\mathit{def}}+\frac{\unicode[STIX]{x1D707}}{2}\int _{\unicode[STIX]{x1D6FA}_{\mathit{obs}}}|V_{m}(\cdot ,T)|^{2}\text{d}\unicode[STIX]{x1D6FA}+\frac{\unicode[STIX]{x1D6FC}}{2}\mathop{\sum }_{k=1}^{N_{el}}\int _{0}^{T}|u_{k}|^{2}\text{d}t\end{eqnarray}$$
can be minimized, accounting for (i) a minimum time term, (ii) a final time observation at
![]() $t=T$
, and (iii) the amplitude of the applied currents, subject to the state system (9.15) to be solved over
$t=T$
, and (iii) the amplitude of the applied currents, subject to the state system (9.15) to be solved over
![]() $(0,T)$
. Indeed, the shock duration and its energy have to be minimized to avoid negative side effects of the applied shock, while the final time observation term is taken into account to quantify defibrillation, thus requiring that the tissue reaches a non-excited state at
$(0,T)$
. Indeed, the shock duration and its energy have to be minimized to avoid negative side effects of the applied shock, while the final time observation term is taken into account to quantify defibrillation, thus requiring that the tissue reaches a non-excited state at
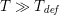 $T\gg T_{\mathit{def}}$
.
$T\gg T_{\mathit{def}}$
.
For illustration, we consider the case of an axially symmetric domain
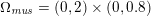 $\unicode[STIX]{x1D6FA}_{\mathit{mus}}=(0,2)\times (0,0.8)$
, where a constant pulse of intensity
$\unicode[STIX]{x1D6FA}_{\mathit{mus}}=(0,2)\times (0,0.8)$
, where a constant pulse of intensity
![]() $u$
is delivered in the control domain
$u$
is delivered in the control domain
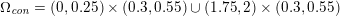 $\unicode[STIX]{x1D6FA}_{\mathit{con}}=(0,0.25)\times (0.3,0.55)\cup (1.75,2)\times (0.3,0.55)$
, until time
$\unicode[STIX]{x1D6FA}_{\mathit{con}}=(0,0.25)\times (0.3,0.55)\cup (1.75,2)\times (0.3,0.55)$
, until time
![]() $T_{\mathit{def}}$
. Here
$T_{\mathit{def}}$
. Here
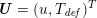 $\boldsymbol{U}=(u,T_{\mathit{def}})^{T}$
is the control variable, with
$\boldsymbol{U}=(u,T_{\mathit{def}})^{T}$
is the control variable, with
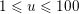 $1\leq u\leq 100$
mV and
$1\leq u\leq 100$
mV and
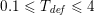 $0.1\leq T_{\mathit{def}}\leq 4$
ms; the final time is
$0.1\leq T_{\mathit{def}}\leq 4$
ms; the final time is
![]() $T=64$
ms. The initial condition
$T=64$
ms. The initial condition
 $(V_{m,0},w_{0})^{T}$
describes a re-entry wave of the ‘figure of eight’ type, obtained following the procedure described by Kunisch and Rund (Reference Kunisch and Rund2015), who also take into account more general optimal control problems. For the case at hand, a planar wavefront travelling from the bottom to the top can be damped by imposing an optimal control of intensity
$(V_{m,0},w_{0})^{T}$
describes a re-entry wave of the ‘figure of eight’ type, obtained following the procedure described by Kunisch and Rund (Reference Kunisch and Rund2015), who also take into account more general optimal control problems. For the case at hand, a planar wavefront travelling from the bottom to the top can be damped by imposing an optimal control of intensity
![]() $u\approx 95$
mV until
$u\approx 95$
mV until
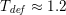 $T_{\mathit{def}}\approx 1.2$
ms on the control region. The successful defibrillation – resulting from a trade-off between a large intensity and a short duration of the pulse – is clearly visible in Figure 9.3, where in the controlled case at the final time the tissue is almost completely unexcited. Indeed, the pulse acts on the excitable region of the tissue adjacent to the wavefront, bringing it to a non-excitable state.
$T_{\mathit{def}}\approx 1.2$
ms on the control region. The successful defibrillation – resulting from a trade-off between a large intensity and a short duration of the pulse – is clearly visible in Figure 9.3, where in the controlled case at the final time the tissue is almost completely unexcited. Indeed, the pulse acts on the excitable region of the tissue adjacent to the wavefront, bringing it to a non-excitable state.

Figure 9.3. Electrical potential at times
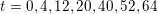 $t=0,4,12,20,40,52,64$
ms in the uncontrolled case (a) and in the controlled case (b). The re-entry wave appearing in the uncontrolled case is damped by the control acting on
$t=0,4,12,20,40,52,64$
ms in the uncontrolled case (a) and in the controlled case (b). The re-entry wave appearing in the uncontrolled case is damped by the control acting on
![]() $\unicode[STIX]{x1D6FA}_{\mathit{con}}$
.
$\unicode[STIX]{x1D6FA}_{\mathit{con}}$
.
Remark 9.3. We point out that choosing the cost functional and, if necessary, imposing suitable constraints on the control and/or the state variable, are two extremely hard, problem-dependent tasks. Moreover, very often control functions are described in terms of (possibly few) relevant parameters, which play the role of design variables. However, in the case of complex, patient-dependent geometries, for example, their automatic selection can result in a fairly involved procedure. Last but not least, in the case where a target state to be reached depends on acquired data, the effect of uncertainty has to be considered in the formulation (and then solution) of the problem. This leads to robust optimization problems, for example, or PDE-constrained optimization problems under uncertainty, an active research field, where very few applications to cardiovascular modelling have yet been considered.
10 Parameter estimation from clinical data
When dealing with the mathematical and numerical modelling of the circulatory system, initial conditions, boundary conditions or physical coefficients, for example tissue properties, might be (partially) unknown (Veneziani and Vergara Reference Veneziani and Vergara2013): see Sections 3 and 6. From here on we refer to any of these quantities as input parameters, independent of their mathematical nature (they could be scalars or vectors, or even parametric fields varying in space) and we refer to the issue of making inferences about unknown parameters from data as parameter estimation (or identification). To perform parameter estimation for a system of PDEs, we need to combine state observations and additional data that are not strictly required for solving the PDE problem, and have to be acquired from measurements.
Parameter estimation for PDEs can be done according to several techniques, which can be roughly classified depending on their outcome (Tarantola Reference Tarantola2004, Le Dimet and Talagrand Reference Le Dimet and Talagrand1986). Point estimates rely on either variational or sequential methods (Ide et al. Reference Ide, Courtier, Ghil and Lorenc1997). Both methods provide optimal least-squares estimates by minimizing a cost functional accounting for the misfit between measured data and state observations. A second class of techniques instead yields confidence regions or, more generally speaking, the possibility of characterizing the probability distribution of the unknown parameters provided they are described in terms of random variables; this is the goal of statistical inversion theory relying for example on Bayesian inference, which will be the main focus of Section 11.2.
In the context of cardiovascular modelling, parameter estimation is necessary for model calibration/personalization, for the purpose of diagnosis or treatment. Indeed, parameters that are not directly measurable (e.g. for tissue conductivity or vessel compliance) are tuned so that the outcome of the numerical model is able to reproduce patient-specific data (Krishnamurthy et al. Reference Krishnamurthy, Villongco, Chuang, Frank, Nigam, Belezzuoli, Stark, Krummen, Narayan, Omens, McCulloch and Kerckhoffs2013). Difficulties arise because of data sparsity (Konukoglu et al. Reference Konukoglu, Relan, Cilingir, Menze, Chinchapatnam, Jadidi, Cochet, Hocini, Delingette, Jaïs, Haïssaguerre, Ayache and Sermesant2011). Indeed, spatial resolution and temporal frequency are typically undersampled; experimental data, on the other hand, are always contaminated by measurement noise.
Remark 10.1. Data assimilation (DA) is the process by which a numerical model of a given system, usually affected by noise or model uncertainties, is improved by incorporating system observations. Although data assimilation relies on the same variational or filtering approaches addressed in this section, in the case of geophysical fluids, for example, its main goal often goes beyond parameter estimation; indeed, it is more often related to state estimation, namely, to improving the outcome of the numerical model and of its initial state to correctly initialize forecasts, by assimilating available measurements into the numerical model itself. Data assimilation is intrinsically related to time-varying phenomena and deals with highly non-linear dynamical systems, very often far from being periodical (such as in the case of meteorological models) and ill-posed: see e.g. Blum, Le Dimet and Navon (Reference Blum, Le dimet, Navon, Temam and Tribbia2009), Voss, Timmer and Kurths (Reference Voss, Timmer and Kurths2004) and Le Dimet and Talagrand (Reference Le Dimet and Talagrand1986) for a detailed discussion. In the past decade several works dealing with cardiovascular applications have focused on data assimilation (Sermesant et al. Reference Sermesant, Moireau, Camara, Sainte-Marie, Andriantsimiavona, Cimrman, Hill, Chapelle and Razavi2006, Delingette et al. Reference Delingette, Billet, Wong, Sermesant, Rhode, Ginks, Rinaldi, Razavi and Ayache2012, Bertagna et al. Reference Bertagna, D’Elia, Perego, Veneziani, Bodnár, Galdi and Nečasová2014, Lal, Mohammadi and Nicoud Reference Lal, Mohammadi and Nicoud2016), which has been considered, in many cases, as synonymous with parameter estimation.
In this section we provide an overview of both variational and sequential approaches for parameter estimation in time-dependent systems. Parameter estimation problems dealing with stationary systems in cardiovascular applications have also been solved: see e.g. D’Elia, Perego and Veneziani (Reference D’Elia, Perego and Veneziani2012), Bertagna et al. (Reference Bertagna, D’Elia, Perego, Veneziani, Bodnár, Galdi and Nečasová2014), MacLachlan et al. (Reference Maclachlan, Nielsen, Lysaker and Tveito2006), Nielsen, Cai and Lykaser (Reference Nielsen, Cai and Lykaser2007a ), Lassila et al. (Reference Lassila, Manzoni, Quarteroni and Rozza2013b ) and Manzoni et al. (Reference Manzoni, Lassila, Quarteroni, Rozza, Bock, Hoang, Rannacher and Schlöder2014). For the sake of space and relevance, we will focus on time-dependent problems.
10.1 Variational approach: PDE-constrained optimization
The variational approach recasts parameter estimation in the framework of PDE-constrained optimization, by considering the equations governing the problem at hand as the state system, and the discrepancy between the observation of the state and the measured data as the cost functional to be minimized (Banks and Kunisch Reference Banks and Kunisch1989, Chavent Reference Chavent2010). The parameters to be estimated (often involving the initial condition) play the role of optimization variables, just like control variables in the case of optimal control problems; however, unlike the optimal control case, the parameters to be estimated are quantities which no one can actually control. They are often coefficients of the operator appearing in the PDE problem.
Here we provide an abstract formulation of the variational approach, following Bertoglio, Moireau and Gerbeau (Reference Bertoglio, Moireau and Gerbeau2012) and Blum et al. (Reference Blum, Le dimet, Navon, Temam and Tribbia2009); for more details see e.g. Nichols (Reference Nichols, Lahoz, Khattatov and Menard2010), Chapelle et al. (Reference Chapelle, Fragu, Mallet and Moireau2013a
) and Sermesant et al. (Reference Sermesant, Moireau, Camara, Sainte-Marie, Andriantsimiavona, Cimrman, Hill, Chapelle and Razavi2006). We assume that the state problem has already been discretized in space. We let
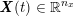 $\boldsymbol{X}(t)\in \mathbb{R}^{n_{x}}$
denote the semi-discrete state,
$\boldsymbol{X}(t)\in \mathbb{R}^{n_{x}}$
denote the semi-discrete state,
![]() $\boldsymbol{\unicode[STIX]{x1D703}}\in \mathbb{R}^{p}$
the parameters of the model to be estimated, and
$\boldsymbol{\unicode[STIX]{x1D703}}\in \mathbb{R}^{p}$
the parameters of the model to be estimated, and
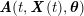 $\boldsymbol{A}(t,\boldsymbol{X}(t),\boldsymbol{\unicode[STIX]{x1D703}})$
the (semi-discretized in space) state operator; note that usually
$\boldsymbol{A}(t,\boldsymbol{X}(t),\boldsymbol{\unicode[STIX]{x1D703}})$
the (semi-discretized in space) state operator; note that usually
![]() $p\ll n_{x}$
. The state variable then solves the dynamical system
$p\ll n_{x}$
. The state variable then solves the dynamical system
 $$\begin{eqnarray}\displaystyle \displaystyle \dot{\boldsymbol{X}}(t) & = & \displaystyle \boldsymbol{A}(t,\boldsymbol{X}(t),\boldsymbol{\unicode[STIX]{x1D703}}),\quad t\in (0,T),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \dot{\boldsymbol{X}}(t) & = & \displaystyle \boldsymbol{A}(t,\boldsymbol{X}(t),\boldsymbol{\unicode[STIX]{x1D703}}),\quad t\in (0,T),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{X}(0) & = & \displaystyle \boldsymbol{G}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{X}(0) & = & \displaystyle \boldsymbol{G}.\end{eqnarray}$$
 $\boldsymbol{X}=(\boldsymbol{v},p,\boldsymbol{d})$
contains fluid velocity and pressure, and structure displacement, and
$\boldsymbol{X}=(\boldsymbol{v},p,\boldsymbol{d})$
contains fluid velocity and pressure, and structure displacement, and
We consider the case where the parameter vector
![]() $\boldsymbol{\unicode[STIX]{x1D703}}$
is unknown, and for which the estimation problem consists in finding
$\boldsymbol{\unicode[STIX]{x1D703}}$
is unknown, and for which the estimation problem consists in finding
![]() $\widehat{\boldsymbol{\unicode[STIX]{x1D703}}}$
such that the discrepancy between the observation and a set of measurements
$\widehat{\boldsymbol{\unicode[STIX]{x1D703}}}$
such that the discrepancy between the observation and a set of measurements
 $\boldsymbol{Z}(t)\in \mathbb{R}^{n_{z}}$
,
$\boldsymbol{Z}(t)\in \mathbb{R}^{n_{z}}$
,
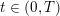 $t\in (0,T)$
, is minimized, for example in a least-squares sense. The case of unknown initial data
$t\in (0,T)$
, is minimized, for example in a least-squares sense. The case of unknown initial data
![]() $\boldsymbol{G}$
to be estimated can be treated in essentially the same way. We usually assume that measurements
$\boldsymbol{G}$
to be estimated can be treated in essentially the same way. We usually assume that measurements
![]() $\boldsymbol{Z}(t)$
are related to observations of the true state through an additive noise model, that is,
$\boldsymbol{Z}(t)$
are related to observations of the true state through an additive noise model, that is,
 $$\begin{eqnarray}\boldsymbol{Z}(t)=H(t)\boldsymbol{X}(t)+\boldsymbol{\unicode[STIX]{x1D700}}(t),\quad t\in (0,T),\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{Z}(t)=H(t)\boldsymbol{X}(t)+\boldsymbol{\unicode[STIX]{x1D700}}(t),\quad t\in (0,T),\end{eqnarray}$$
where
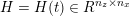 $H=H(t)\in R^{n_{z}\times n_{x}}$
is an observation operator which maps the state space into the observation space
$H=H(t)\in R^{n_{z}\times n_{x}}$
is an observation operator which maps the state space into the observation space
![]() $R^{n_{z}}$
, and
$R^{n_{z}}$
, and
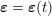 $\boldsymbol{\unicode[STIX]{x1D700}}=\boldsymbol{\unicode[STIX]{x1D700}}(t)$
is a noise term accounting for measurement errors. The following minimization problem is then solved:
$\boldsymbol{\unicode[STIX]{x1D700}}=\boldsymbol{\unicode[STIX]{x1D700}}(t)$
is a noise term accounting for measurement errors. The following minimization problem is then solved:
 $$\begin{eqnarray}J(\boldsymbol{X},\boldsymbol{\unicode[STIX]{x1D703}})=\frac{1}{2}\int _{0}^{T}\Vert \boldsymbol{Z}(t)-H(t)\boldsymbol{X}(t)\Vert _{M}^{2}\text{d}t+\frac{\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D703}}}{2}\Vert \boldsymbol{\unicode[STIX]{x1D703}}-\boldsymbol{\unicode[STIX]{x1D703}}_{0}\Vert _{P_{\unicode[STIX]{x1D703}}^{-1}}^{2}~\rightarrow \min _{\boldsymbol{\unicode[STIX]{x1D703}}\in {\mathcal{P}}},\end{eqnarray}$$
$$\begin{eqnarray}J(\boldsymbol{X},\boldsymbol{\unicode[STIX]{x1D703}})=\frac{1}{2}\int _{0}^{T}\Vert \boldsymbol{Z}(t)-H(t)\boldsymbol{X}(t)\Vert _{M}^{2}\text{d}t+\frac{\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D703}}}{2}\Vert \boldsymbol{\unicode[STIX]{x1D703}}-\boldsymbol{\unicode[STIX]{x1D703}}_{0}\Vert _{P_{\unicode[STIX]{x1D703}}^{-1}}^{2}~\rightarrow \min _{\boldsymbol{\unicode[STIX]{x1D703}}\in {\mathcal{P}}},\end{eqnarray}$$
where
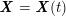 $\boldsymbol{X}=\boldsymbol{X}(t)$
is the solution of (10.1). Here
$\boldsymbol{X}=\boldsymbol{X}(t)$
is the solution of (10.1). Here
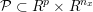 ${\mathcal{P}}\subset R^{p}\times R^{n_{x}}$
denotes the set of admissible parameters. Additional information is usually added to the least-squares objective expressed by the first term in (10.2), via a background estimate
${\mathcal{P}}\subset R^{p}\times R^{n_{x}}$
denotes the set of admissible parameters. Additional information is usually added to the least-squares objective expressed by the first term in (10.2), via a background estimate
![]() $\boldsymbol{\unicode[STIX]{x1D703}}_{0}$
of
$\boldsymbol{\unicode[STIX]{x1D703}}_{0}$
of
![]() $\boldsymbol{\unicode[STIX]{x1D703}}$
;
$\boldsymbol{\unicode[STIX]{x1D703}}$
;
![]() $M$
and
$M$
and
![]() $P_{\unicode[STIX]{x1D703}}^{-1}$
are suitable symmetric positive definite matrices (the reason why we consider an inverse matrix to define this latter norm will be clarified in the following). This procedure goes by the name of Levenberg–Marquardt–Tikhonov regularization. For a discussion of classical regularization methods for inverse problems, see Kaipio and Somersalo (Reference Kaipio and Somersalo2005); note that the usual penalization coefficients are embedded in the definition of the matrix
$P_{\unicode[STIX]{x1D703}}^{-1}$
are suitable symmetric positive definite matrices (the reason why we consider an inverse matrix to define this latter norm will be clarified in the following). This procedure goes by the name of Levenberg–Marquardt–Tikhonov regularization. For a discussion of classical regularization methods for inverse problems, see Kaipio and Somersalo (Reference Kaipio and Somersalo2005); note that the usual penalization coefficients are embedded in the definition of the matrix
![]() $P_{\unicode[STIX]{x1D703}}^{-1}$
.
$P_{\unicode[STIX]{x1D703}}^{-1}$
.
The minimization problem (10.2) can be solved by an optimization algorithm based on the evaluation of the gradient of
![]() $J$
with respect to
$J$
with respect to
![]() $\boldsymbol{\unicode[STIX]{x1D703}}$
. As shown in Section 9.1, this latter can be computed by relying on the solution of a suitable adjoint problem. This is a four-dimensional variational (4D-Var) assimilation; a three-dimensional variational (3D-Var) assimilation would arise in the case of steady-state systems. See Section 10.3.1 for further details on a relevant example in cardiovascular modelling, and Blum et al. (Reference Blum, Le dimet, Navon, Temam and Tribbia2009) and Chapelle et al. (Reference Chapelle, Fragu, Mallet and Moireau2013a
) for more on 4D-Var assimilation problems.
$\boldsymbol{\unicode[STIX]{x1D703}}$
. As shown in Section 9.1, this latter can be computed by relying on the solution of a suitable adjoint problem. This is a four-dimensional variational (4D-Var) assimilation; a three-dimensional variational (3D-Var) assimilation would arise in the case of steady-state systems. See Section 10.3.1 for further details on a relevant example in cardiovascular modelling, and Blum et al. (Reference Blum, Le dimet, Navon, Temam and Tribbia2009) and Chapelle et al. (Reference Chapelle, Fragu, Mallet and Moireau2013a
) for more on 4D-Var assimilation problems.
Since measurements
![]() $\boldsymbol{Z}$
are only available at a discrete number of times
$\boldsymbol{Z}$
are only available at a discrete number of times
 $\unicode[STIX]{x1D70F}^{1},\ldots ,\unicode[STIX]{x1D70F}^{K}$
, we formulate the identification problem by replacing the dynamical system (10.1) with its time-discretized version:
$\unicode[STIX]{x1D70F}^{1},\ldots ,\unicode[STIX]{x1D70F}^{K}$
, we formulate the identification problem by replacing the dynamical system (10.1) with its time-discretized version:
 $$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{X}^{k+1} & = & \displaystyle \boldsymbol{A}_{k|k+1}(\boldsymbol{X}^{k},\boldsymbol{\unicode[STIX]{x1D703}}),\quad k=0,\ldots ,K-1,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{X}^{k+1} & = & \displaystyle \boldsymbol{A}_{k|k+1}(\boldsymbol{X}^{k},\boldsymbol{\unicode[STIX]{x1D703}}),\quad k=0,\ldots ,K-1,\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \boldsymbol{X}^{0} & = & \displaystyle \boldsymbol{G}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{X}^{0} & = & \displaystyle \boldsymbol{G}\end{eqnarray}$$
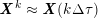 $\boldsymbol{X}^{k}\approx \boldsymbol{X}(k\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D70F})$
denotes the state vector at time
$\boldsymbol{X}^{k}\approx \boldsymbol{X}(k\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D70F})$
denotes the state vector at time
 $\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D70F}^{k+1}-\unicode[STIX]{x1D70F}^{k}$
of the time window between two subsequent measurements is usually larger than the time step
$\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D70F}^{k+1}-\unicode[STIX]{x1D70F}^{k}$
of the time window between two subsequent measurements is usually larger than the time step
We then formulate an optimal time-discretized minimization criterion and, finally, determine the corresponding adjoint problem, rather than discretizing the adjoint problem in time. This yields the minimization problem
 $$\begin{eqnarray}J_{K}(\boldsymbol{X},\boldsymbol{\unicode[STIX]{x1D703}})=\frac{1}{2}\mathop{\sum }_{k=1}^{K}\Vert \boldsymbol{Z}^{k}-H\boldsymbol{X}^{k}\Vert _{M_{k}}^{2}+\frac{1}{2}\Vert \boldsymbol{\unicode[STIX]{x1D703}}-\boldsymbol{\unicode[STIX]{x1D703}}_{0}\Vert _{P_{\unicode[STIX]{x1D703}}^{-1}}^{2}~\rightarrow \min _{\boldsymbol{\unicode[STIX]{x1D703}}\in {\mathcal{P}}},\end{eqnarray}$$
$$\begin{eqnarray}J_{K}(\boldsymbol{X},\boldsymbol{\unicode[STIX]{x1D703}})=\frac{1}{2}\mathop{\sum }_{k=1}^{K}\Vert \boldsymbol{Z}^{k}-H\boldsymbol{X}^{k}\Vert _{M_{k}}^{2}+\frac{1}{2}\Vert \boldsymbol{\unicode[STIX]{x1D703}}-\boldsymbol{\unicode[STIX]{x1D703}}_{0}\Vert _{P_{\unicode[STIX]{x1D703}}^{-1}}^{2}~\rightarrow \min _{\boldsymbol{\unicode[STIX]{x1D703}}\in {\mathcal{P}}},\end{eqnarray}$$
where
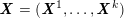 $\boldsymbol{X}=(\boldsymbol{X}^{1},\ldots ,\boldsymbol{X}^{k})$
, and we set
$\boldsymbol{X}=(\boldsymbol{X}^{1},\ldots ,\boldsymbol{X}^{k})$
, and we set
 $$\begin{eqnarray}\boldsymbol{Z}^{k}=H_{k}\boldsymbol{X}^{k}+\boldsymbol{\unicode[STIX]{x1D700}}^{k}.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{Z}^{k}=H_{k}\boldsymbol{X}^{k}+\boldsymbol{\unicode[STIX]{x1D700}}^{k}.\end{eqnarray}$$
Here
![]() $\boldsymbol{\unicode[STIX]{x1D700}}^{k}$
denotes the noise of the measurement device at
$\boldsymbol{\unicode[STIX]{x1D700}}^{k}$
denotes the noise of the measurement device at
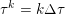 $\unicode[STIX]{x1D70F}^{k}=k\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D70F}$
; a possible choice for
$\unicode[STIX]{x1D70F}^{k}=k\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D70F}$
; a possible choice for
![]() $M_{k}$
is
$M_{k}$
is
 $M_{k}=\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D70F}M$
, whereas
$M_{k}=\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D70F}M$
, whereas
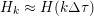 $H_{k}\approx H(k\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D70F})$
. Also in this case a gradient-based optimization procedure can be used to solve the constrained optimization problem (10.3, 10.4) with gradients evaluated by introducing a suitable adjoint problem.
$H_{k}\approx H(k\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D70F})$
. Also in this case a gradient-based optimization procedure can be used to solve the constrained optimization problem (10.3, 10.4) with gradients evaluated by introducing a suitable adjoint problem.
10.2 Sequential approach: Kalman filter and extensions
A drawback of the variational approach is the need to wait until the whole set of measurements has been acquired in order to perform an optimization step. A sequential approach instead performs the assimilation of acquired measurements on the fly, and updates the estimate of the unknown quantities accordingly.
A numerical milestone for the solution of sequential estimation problems, the Kalman filter (KF) (Kalman Reference Kalman1960), was introduced as a recursive filter for the estimation of the state of a noisy dynamical system from a set of measurements, that is, to improve the prediction of the state dynamics by taking into account additional data. An augmented form of the Kalman filter can be easily adapted to the problem of estimating unknown parameters, as we will see. Originally designed for linear dynamical systems, the Kalman filter has severe memory requirements. To mitigate these two limitations, several improvements and extensions have been proposed in the past few decades, most notably the extended Kalman filter (EKF), the unscented Kalman filter (UKF) and the ensemble Kalman filter (EnKF); detailed reviews can be found, for example, in Kaipio and Somersalo (Reference Kaipio and Somersalo2005), Simon (Reference Simon2006), Humpherys, Redd and West (Reference Humpherys, Redd and West2012) and Asch, Bocquet and Nodet (Reference Asch, Bocquet and Nodet2017). In this section we recall the formulation of the basic Kalman filter and provide some hints about its extensions, with a special focus on the field of cardiovascular modelling where these techniques have been applied.
The literature offers many possible derivations of the Kalman filter; following Humpherys et al. (Reference Humpherys, Redd and West2012) and Chapelle et al. (Reference Chapelle, Fragu, Mallet and Moireau2013a ), we will exploit the analogy with the solution of a recursive least-squares problem yielding the best linear unbiased estimator for a linear model; alternative derivations can be obtained, for example, by relying on the so-called push-forward and subsequent conditioning of Gaussian measures (Sullivan Reference Sullivan2015) or a sequential Bayesian estimation framework (Law, Stuart and Zygalakis Reference Law, Stuart and Zygalakis2015).
10.2.1 The Kalman filter algorithm
The KF algorithm sequentially generates an estimate of the unknown quantity by means of a linear combination of the current estimate and the acquired measurement. Let us first consider the case where there is no dynamics, and data are generated by the linear model
 $$\begin{eqnarray}\boldsymbol{Z}=H\boldsymbol{X}+\boldsymbol{\unicode[STIX]{x1D700}},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{Z}=H\boldsymbol{X}+\boldsymbol{\unicode[STIX]{x1D700}},\end{eqnarray}$$
where
![]() $H$
is a given
$H$
is a given
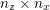 $n_{z}\times n_{x}$
matrix of rank
$n_{z}\times n_{x}$
matrix of rank
![]() $n_{x}$
,
$n_{x}$
,
![]() $\boldsymbol{\unicode[STIX]{x1D700}}$
is an
$\boldsymbol{\unicode[STIX]{x1D700}}$
is an
![]() $n_{z}$
-dimensional random variable with zero mean and known positive definite covariance
$n_{z}$
-dimensional random variable with zero mean and known positive definite covariance
 $Q=\mathbb{E}[\boldsymbol{\unicode[STIX]{x1D700}}\boldsymbol{\unicode[STIX]{x1D700}}^{T}]>0$
, and
$Q=\mathbb{E}[\boldsymbol{\unicode[STIX]{x1D700}}\boldsymbol{\unicode[STIX]{x1D700}}^{T}]>0$
, and
![]() $\boldsymbol{Z}$
denotes known, but inexact, measurements with errors given by
$\boldsymbol{Z}$
denotes known, but inexact, measurements with errors given by
![]() $\boldsymbol{\unicode[STIX]{x1D700}}$
. The vector
$\boldsymbol{\unicode[STIX]{x1D700}}$
. The vector
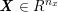 $\boldsymbol{X}\in R^{n_{x}}$
is the quantity to be estimated from the observation
$\boldsymbol{X}\in R^{n_{x}}$
is the quantity to be estimated from the observation
![]() $\boldsymbol{Z}$
;
$\boldsymbol{Z}$
;
![]() $\mathbb{E}[\cdot ]$
denotes the expected value.
$\mathbb{E}[\cdot ]$
denotes the expected value.
Among all linear estimators of
![]() $\boldsymbol{X}$
, that is, estimators of the form
$\boldsymbol{X}$
, that is, estimators of the form
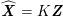 $\widehat{\boldsymbol{X}}=K\boldsymbol{Z}$
for some matrix
$\widehat{\boldsymbol{X}}=K\boldsymbol{Z}$
for some matrix
 $K\in R^{n_{x}\times n_{z}}$
, which are unbiased (i.e.
$K\in R^{n_{x}\times n_{z}}$
, which are unbiased (i.e.
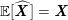 $\mathbb{E}[\widehat{\boldsymbol{X}}]=\boldsymbol{X}$
), the best choice is the one that minimizes the mean-square error
$\mathbb{E}[\widehat{\boldsymbol{X}}]=\boldsymbol{X}$
), the best choice is the one that minimizes the mean-square error
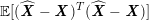 $\mathbb{E}[(\widehat{\boldsymbol{X}}-\boldsymbol{X})^{T}(\widehat{\boldsymbol{X}}-\boldsymbol{X})]$
; by the Gauss–Markov theorem (see e.g. Sullivan Reference Sullivan2015, Chapter 7), the best or minimum variance linear unbiased estimator for (10.6) is given by
$\mathbb{E}[(\widehat{\boldsymbol{X}}-\boldsymbol{X})^{T}(\widehat{\boldsymbol{X}}-\boldsymbol{X})]$
; by the Gauss–Markov theorem (see e.g. Sullivan Reference Sullivan2015, Chapter 7), the best or minimum variance linear unbiased estimator for (10.6) is given by
 $$\begin{eqnarray}\widehat{\boldsymbol{X}}=(H^{T}Q^{-1}H)^{-1}H^{T}Q^{-1}\boldsymbol{Z}.\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\boldsymbol{X}}=(H^{T}Q^{-1}H)^{-1}H^{T}Q^{-1}\boldsymbol{Z}.\end{eqnarray}$$
In that case,
 $E[(\widehat{\boldsymbol{X}}-\boldsymbol{X})(\widehat{\boldsymbol{X}}-\boldsymbol{X})^{T}]=(H^{T}Q^{-1}H)^{-1}$
. Equivalently, (10.7) can also be obtained by solving the weighted least-squares problem
$E[(\widehat{\boldsymbol{X}}-\boldsymbol{X})(\widehat{\boldsymbol{X}}-\boldsymbol{X})^{T}]=(H^{T}Q^{-1}H)^{-1}$
. Equivalently, (10.7) can also be obtained by solving the weighted least-squares problem
 $$\begin{eqnarray}\widehat{\boldsymbol{X}}=\frac{1}{2}\Vert H\boldsymbol{X}-\boldsymbol{Z}\Vert _{Q^{-1}}^{2}\rightarrow \min _{\boldsymbol{ X}},\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\boldsymbol{X}}=\frac{1}{2}\Vert H\boldsymbol{X}-\boldsymbol{Z}\Vert _{Q^{-1}}^{2}\rightarrow \min _{\boldsymbol{ X}},\end{eqnarray}$$
again resorting to a variational argument. In the slightly different case where we want to combine the observation and a background estimate
![]() $\boldsymbol{X}_{0}$
of
$\boldsymbol{X}_{0}$
of
![]() $\boldsymbol{X}$
with covariance
$\boldsymbol{X}$
with covariance
![]() $P^{-}$
, (10.8) becomes
$P^{-}$
, (10.8) becomes
 $$\begin{eqnarray}\widehat{\boldsymbol{X}}=\frac{1}{2}\Vert H\boldsymbol{X}-\boldsymbol{Z}\Vert _{Q^{-1}}^{2}+\frac{1}{2}\Vert \boldsymbol{X}-\boldsymbol{X}_{0}\Vert _{(P^{-})^{-1}}^{2}\rightarrow \min _{\boldsymbol{ X}},\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\boldsymbol{X}}=\frac{1}{2}\Vert H\boldsymbol{X}-\boldsymbol{Z}\Vert _{Q^{-1}}^{2}+\frac{1}{2}\Vert \boldsymbol{X}-\boldsymbol{X}_{0}\Vert _{(P^{-})^{-1}}^{2}\rightarrow \min _{\boldsymbol{ X}},\end{eqnarray}$$
and instead of (10.7) we find
 $$\begin{eqnarray}\widehat{\boldsymbol{X}}=\boldsymbol{X}_{0}+K(\boldsymbol{Z}-H\boldsymbol{X}_{0}),\quad K=P^{+}H^{T}Q^{-1},\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\boldsymbol{X}}=\boldsymbol{X}_{0}+K(\boldsymbol{Z}-H\boldsymbol{X}_{0}),\quad K=P^{+}H^{T}Q^{-1},\end{eqnarray}$$
upon defining the matrix playing the role of updated covariance as
 $$\begin{eqnarray}P^{+}=((P^{-})^{-1}+H^{T}Q^{-1}H)^{-1}.\end{eqnarray}$$
$$\begin{eqnarray}P^{+}=((P^{-})^{-1}+H^{T}Q^{-1}H)^{-1}.\end{eqnarray}$$
Note that this estimate is given by a linear combination of the background estimate
![]() $\boldsymbol{X}_{0}$
and the so-called innovation
$\boldsymbol{X}_{0}$
and the so-called innovation
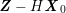 $\boldsymbol{Z}-H\boldsymbol{X}_{0}$
.
$\boldsymbol{Z}-H\boldsymbol{X}_{0}$
.
![]() $K$
is usually referred to as the Kalman gain matrix; it can also be evaluated by exploiting the prior covariance
$K$
is usually referred to as the Kalman gain matrix; it can also be evaluated by exploiting the prior covariance
![]() $P^{-}$
instead of the updated covariance
$P^{-}$
instead of the updated covariance
![]() $P^{+}$
, according to the equivalence
$P^{+}$
, according to the equivalence
 $$\begin{eqnarray}P^{+}H^{T}Q^{-1}=P^{-}H^{T}(HP^{-}H^{T}+Q)^{-1}.\end{eqnarray}$$
$$\begin{eqnarray}P^{+}H^{T}Q^{-1}=P^{-}H^{T}(HP^{-}H^{T}+Q)^{-1}.\end{eqnarray}$$
We now consider the case of a time-discretized linear system, with data acquired over a time interval. Then the model (10.6) is replaced by
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}l@{}}\boldsymbol{X}^{k}=A_{k-1|k}\boldsymbol{X}^{k-1}+\boldsymbol{v}^{k},\quad k=1,\ldots ,K,~\boldsymbol{X}^{0}=\boldsymbol{G},\\ \boldsymbol{Z}^{k}=H_{k}\boldsymbol{X}^{k}+\boldsymbol{w}^{k},\end{array} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}l@{}}\boldsymbol{X}^{k}=A_{k-1|k}\boldsymbol{X}^{k-1}+\boldsymbol{v}^{k},\quad k=1,\ldots ,K,~\boldsymbol{X}^{0}=\boldsymbol{G},\\ \boldsymbol{Z}^{k}=H_{k}\boldsymbol{X}^{k}+\boldsymbol{w}^{k},\end{array} & & \displaystyle\end{eqnarray}$$
where
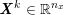 $\boldsymbol{X}^{k}\in \mathbb{R}^{n_{x}}$
denotes the state and
$\boldsymbol{X}^{k}\in \mathbb{R}^{n_{x}}$
denotes the state and
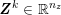 $\boldsymbol{Z}^{k}\in \mathbb{R}^{n_{z}}$
are the measurements;
$\boldsymbol{Z}^{k}\in \mathbb{R}^{n_{z}}$
are the measurements;
![]() $\boldsymbol{v}_{k}$
and
$\boldsymbol{v}_{k}$
and
![]() $\boldsymbol{w}_{k}$
are uncorrelated zero-mean random noise processes with positive definite covariances
$\boldsymbol{w}_{k}$
are uncorrelated zero-mean random noise processes with positive definite covariances
![]() $Q_{k}$
and
$Q_{k}$
and
![]() $R_{k}$
, modelling the uncertainty of the model and the additive noise in the observation, respectively. The state estimation problem is the problem of finding the state
$R_{k}$
, modelling the uncertainty of the model and the additive noise in the observation, respectively. The state estimation problem is the problem of finding the state
![]() $\boldsymbol{X}^{k}$
given
$\boldsymbol{X}^{k}$
given
![]() $k$
known observations
$k$
known observations
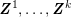 $\boldsymbol{Z}^{1},\ldots ,\boldsymbol{Z}^{k}$
.
$\boldsymbol{Z}^{1},\ldots ,\boldsymbol{Z}^{k}$
.
The Kalman filter is a recursive algorithm that provides the best linear unbiased estimate
![]() $\boldsymbol{X}_{a}^{k}$
of
$\boldsymbol{X}_{a}^{k}$
of
![]() $\boldsymbol{X}^{k}$
in terms of both the previous estimate
$\boldsymbol{X}^{k}$
in terms of both the previous estimate
![]() $\boldsymbol{X}_{a}^{k-1}$
and the latest data
$\boldsymbol{X}_{a}^{k-1}$
and the latest data
![]() $\boldsymbol{Z}^{k}$
up to that point in time. It is based on a predictor-corrector strategy, consisting of the following steps.
$\boldsymbol{Z}^{k}$
up to that point in time. It is based on a predictor-corrector strategy, consisting of the following steps.
-
(1) A prediction step (called the forecast or the time update) consists in letting the system dynamics evolve from
 $\boldsymbol{X}_{a}^{k-1}$
without taking into account the observations, yielding the forecast state
$\boldsymbol{X}_{a}^{k-1}$
without taking into account the observations, yielding the forecast state
 $\boldsymbol{X}_{f}^{k}$
.
$\boldsymbol{X}_{f}^{k}$
. -
(2) A correction step (called the analysis or the measurement update) updates the forecast state
 $\boldsymbol{X}_{f}^{k}$
by assimilating the measurements into the model, yielding the assimilated state
$\boldsymbol{X}_{f}^{k}$
by assimilating the measurements into the model, yielding the assimilated state
 $\boldsymbol{X}_{a}^{k}$
.
$\boldsymbol{X}_{a}^{k}$
.
To derive the expression of the correction step, let us suppose that the current prediction based on observations
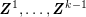 $\boldsymbol{Z}^{1},\ldots ,\boldsymbol{Z}^{k-1}$
is
$\boldsymbol{Z}^{1},\ldots ,\boldsymbol{Z}^{k-1}$
is
![]() $\boldsymbol{X}_{f}^{k}$
, with covariance matrix
$\boldsymbol{X}_{f}^{k}$
, with covariance matrix
![]() $P_{k}^{f}$
. If the true state is
$P_{k}^{f}$
. If the true state is
![]() $\boldsymbol{X}_{k}$
, model (10.6) becomes
$\boldsymbol{X}_{k}$
, model (10.6) becomes
 $$\begin{eqnarray}\left[\begin{array}{@{}c@{}}\boldsymbol{X}_{f}^{k}\\ \boldsymbol{Z}^{k}\end{array}\right]=\left[\begin{array}{@{}c@{}}I\\ H_{k}\end{array}\right]\boldsymbol{ X}^{k}+\boldsymbol{\unicode[STIX]{x1D700}},\end{eqnarray}$$
$$\begin{eqnarray}\left[\begin{array}{@{}c@{}}\boldsymbol{X}_{f}^{k}\\ \boldsymbol{Z}^{k}\end{array}\right]=\left[\begin{array}{@{}c@{}}I\\ H_{k}\end{array}\right]\boldsymbol{ X}^{k}+\boldsymbol{\unicode[STIX]{x1D700}},\end{eqnarray}$$
where
![]() $\boldsymbol{\unicode[STIX]{x1D700}}$
is an
$\boldsymbol{\unicode[STIX]{x1D700}}$
is an
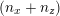 $(n_{x}+n_{z})$
-dimensional random variable with zero mean and covariance
$(n_{x}+n_{z})$
-dimensional random variable with zero mean and covariance
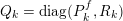 $Q_{k}=\operatorname{diag}(P_{k}^{f},R_{k})$
. The best linear unbiased estimator of this system (see (10.7)) is given by
$Q_{k}=\operatorname{diag}(P_{k}^{f},R_{k})$
. The best linear unbiased estimator of this system (see (10.7)) is given by
 $$\begin{eqnarray}\boldsymbol{X}_{a}^{k}=P_{k}^{a}\left[\begin{array}{@{}c@{}}I\quad H_{k}^{T}\end{array}\right]\left[\begin{array}{@{}cc@{}}(P_{k}^{f})^{-1} & 0\\ 0 & R_{k}^{-1}\end{array}\right]\left[\begin{array}{@{}c@{}}\boldsymbol{X}_{f}^{k}\\ \boldsymbol{Z}^{k}\end{array}\right]=P_{k}^{a}((P_{k}^{f})^{-1}\boldsymbol{X}_{f}^{k}+H_{k}^{T}R_{k}^{-1}\boldsymbol{Z}^{k}),\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{X}_{a}^{k}=P_{k}^{a}\left[\begin{array}{@{}c@{}}I\quad H_{k}^{T}\end{array}\right]\left[\begin{array}{@{}cc@{}}(P_{k}^{f})^{-1} & 0\\ 0 & R_{k}^{-1}\end{array}\right]\left[\begin{array}{@{}c@{}}\boldsymbol{X}_{f}^{k}\\ \boldsymbol{Z}^{k}\end{array}\right]=P_{k}^{a}((P_{k}^{f})^{-1}\boldsymbol{X}_{f}^{k}+H_{k}^{T}R_{k}^{-1}\boldsymbol{Z}^{k}),\end{eqnarray}$$
and results from the linear combination of the current estimate and the last observation
![]() $\boldsymbol{Z}^{k}$
, where
$\boldsymbol{Z}^{k}$
, where
 $$\begin{eqnarray}P_{k}^{a}=\biggl(\left[\begin{array}{@{}c@{}}I\quad H_{k}^{T}\end{array}\right]\left[\begin{array}{@{}cc@{}}(P_{k}^{f})^{-1} & 0\\ 0 & R_{k}^{-1}\end{array}\right]\left[\begin{array}{@{}c@{}}I\\ H_{k}\end{array}\right]\biggr)^{-1}=((P_{k}^{f})^{-1}+H_{k}^{T}R_{k}^{-1}H_{k})^{-1}.\end{eqnarray}$$
$$\begin{eqnarray}P_{k}^{a}=\biggl(\left[\begin{array}{@{}c@{}}I\quad H_{k}^{T}\end{array}\right]\left[\begin{array}{@{}cc@{}}(P_{k}^{f})^{-1} & 0\\ 0 & R_{k}^{-1}\end{array}\right]\left[\begin{array}{@{}c@{}}I\\ H_{k}\end{array}\right]\biggr)^{-1}=((P_{k}^{f})^{-1}+H_{k}^{T}R_{k}^{-1}H_{k})^{-1}.\end{eqnarray}$$
Note the formal analogy with (10.10), where
![]() $P_{k}^{f}$
and
$P_{k}^{f}$
and
![]() $P_{k}^{a}$
now play the role of
$P_{k}^{a}$
now play the role of
![]() $P^{-}$
and
$P^{-}$
and
![]() $P^{+}$
, respectively. Equation (10.13) can be written in the more convenient form
$P^{+}$
, respectively. Equation (10.13) can be written in the more convenient form
 $$\begin{eqnarray}\displaystyle \boldsymbol{X}_{a}^{k} & = & \displaystyle P_{k}^{a}[(P_{k}^{a})^{-1}-H_{k}^{T}R_{k}^{-1}H_{k} ))\boldsymbol{X}_{f}^{k}+H_{k}^{T}R_{k}^{-1}\boldsymbol{Z}^{k}]\nonumber\\ \displaystyle & = & \displaystyle \boldsymbol{X}_{f}^{k}+P_{k}^{a}H_{k}^{T}R_{k}^{-1}(\boldsymbol{Z}^{k}-H_{k}\boldsymbol{X}_{f}^{k})=\boldsymbol{X}_{f}^{k}+K_{k}(\boldsymbol{Z}^{k}-H_{k}\boldsymbol{X}_{f}^{k})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{X}_{a}^{k} & = & \displaystyle P_{k}^{a}[(P_{k}^{a})^{-1}-H_{k}^{T}R_{k}^{-1}H_{k} ))\boldsymbol{X}_{f}^{k}+H_{k}^{T}R_{k}^{-1}\boldsymbol{Z}^{k}]\nonumber\\ \displaystyle & = & \displaystyle \boldsymbol{X}_{f}^{k}+P_{k}^{a}H_{k}^{T}R_{k}^{-1}(\boldsymbol{Z}^{k}-H_{k}\boldsymbol{X}_{f}^{k})=\boldsymbol{X}_{f}^{k}+K_{k}(\boldsymbol{Z}^{k}-H_{k}\boldsymbol{X}_{f}^{k})\nonumber\end{eqnarray}$$
as a function of the innovation
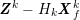 $\boldsymbol{Z}^{k}-H_{k}\boldsymbol{X}_{f}^{k}$
. Similarly to (10.11), we obtain
$\boldsymbol{Z}^{k}-H_{k}\boldsymbol{X}_{f}^{k}$
. Similarly to (10.11), we obtain
 $$\begin{eqnarray}K_{k}=P_{k}^{a}H_{k}^{T}R_{k}^{-1}=P_{k}^{f}H_{k}^{T}(H_{k}P_{k}^{f}H^{T}+R_{k})^{-1},\end{eqnarray}$$
$$\begin{eqnarray}K_{k}=P_{k}^{a}H_{k}^{T}R_{k}^{-1}=P_{k}^{f}H_{k}^{T}(H_{k}P_{k}^{f}H^{T}+R_{k})^{-1},\end{eqnarray}$$
so it is possible to evaluate the Kalman gain matrix
![]() $K_{k}$
as a function of
$K_{k}$
as a function of
![]() $P_{k}^{f}$
, and then correct the covariance:
$P_{k}^{f}$
, and then correct the covariance:
 $$\begin{eqnarray}\displaystyle P_{k}^{a} & = & \displaystyle ((P_{k}^{f})^{-1}+H_{k}^{T}R_{k}^{-1}H_{k})^{-1}\nonumber\\ \displaystyle & = & \displaystyle (I-K_{k}H_{k})P_{k}^{f}(I-K_{k}H_{k})^{T}+K_{k}R_{k}K_{k}^{T}=(I-K_{k}H_{k})P_{k}^{f}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P_{k}^{a} & = & \displaystyle ((P_{k}^{f})^{-1}+H_{k}^{T}R_{k}^{-1}H_{k})^{-1}\nonumber\\ \displaystyle & = & \displaystyle (I-K_{k}H_{k})P_{k}^{f}(I-K_{k}H_{k})^{T}+K_{k}R_{k}K_{k}^{T}=(I-K_{k}H_{k})P_{k}^{f}.\nonumber\end{eqnarray}$$
The prediction step instead exploits the dynamical system to propagate the state, yielding
 $$\begin{eqnarray}\boldsymbol{X}_{f}^{k+1}=A_{k|k+1}\boldsymbol{X}_{a}^{k}\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{X}_{f}^{k+1}=A_{k|k+1}\boldsymbol{X}_{a}^{k}\end{eqnarray}$$
for the time update of the state, and
 $$\begin{eqnarray}\displaystyle P_{k+1}^{f} & = & \displaystyle \mathbb{E}[(\boldsymbol{X}_{f}^{k+1}-\boldsymbol{X}^{k+1})(\boldsymbol{X}_{f}^{k+1}-\boldsymbol{X}^{k+1})^{T}]\nonumber\\ \displaystyle & = & \displaystyle \mathbb{E}[(A_{k|k+1}\boldsymbol{X}_{a}^{k}-A_{k|k+1}\boldsymbol{X}_{k}-\boldsymbol{w}_{k})(A_{k|k+1}\widehat{\boldsymbol{X}}_{a}^{k}-A_{k|k+1}\boldsymbol{X}_{k}-\boldsymbol{w}_{k})^{T}]\nonumber\\ \displaystyle & = & \displaystyle A_{k|k+1}P_{k}^{a}A_{k|k+1}^{T}+Q_{k+1}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P_{k+1}^{f} & = & \displaystyle \mathbb{E}[(\boldsymbol{X}_{f}^{k+1}-\boldsymbol{X}^{k+1})(\boldsymbol{X}_{f}^{k+1}-\boldsymbol{X}^{k+1})^{T}]\nonumber\\ \displaystyle & = & \displaystyle \mathbb{E}[(A_{k|k+1}\boldsymbol{X}_{a}^{k}-A_{k|k+1}\boldsymbol{X}_{k}-\boldsymbol{w}_{k})(A_{k|k+1}\widehat{\boldsymbol{X}}_{a}^{k}-A_{k|k+1}\boldsymbol{X}_{k}-\boldsymbol{w}_{k})^{T}]\nonumber\\ \displaystyle & = & \displaystyle A_{k|k+1}P_{k}^{a}A_{k|k+1}^{T}+Q_{k+1}\nonumber\end{eqnarray}$$
for the time update of the covariance.
Grouping the prediction and the correction steps together, we finally obtain the
![]() $k$
th step of the KF algorithm:
$k$
th step of the KF algorithm:
 $$\begin{eqnarray}\displaystyle \boldsymbol{X}_{f}^{k}=A_{k-1|k}\boldsymbol{X}_{a}^{k-1} & & \displaystyle \text{state prediction,}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{X}_{f}^{k}=A_{k-1|k}\boldsymbol{X}_{a}^{k-1} & & \displaystyle \text{state prediction,}\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle P_{k}^{f}=A_{k-1|k}P_{k-1}^{a}A_{k-1|k}^{T}+Q_{k} & & \displaystyle \text{error covariance prediction,}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P_{k}^{f}=A_{k-1|k}P_{k-1}^{a}A_{k-1|k}^{T}+Q_{k} & & \displaystyle \text{error covariance prediction,}\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle K_{k}=P_{f}^{k}H_{k}^{T}(H_{k}P_{k}^{f}H_{k}^{T}+R_{k})^{-1} & & \displaystyle \text{Kalman gain evaluation,}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K_{k}=P_{f}^{k}H_{k}^{T}(H_{k}P_{k}^{f}H_{k}^{T}+R_{k})^{-1} & & \displaystyle \text{Kalman gain evaluation,}\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \boldsymbol{X}_{a}^{k}=\boldsymbol{X}_{f}^{k}+K_{k}(\boldsymbol{Z}^{k}-H_{k}\boldsymbol{X}_{f}^{k}) & & \displaystyle \text{state correction,}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{X}_{a}^{k}=\boldsymbol{X}_{f}^{k}+K_{k}(\boldsymbol{Z}^{k}-H_{k}\boldsymbol{X}_{f}^{k}) & & \displaystyle \text{state correction,}\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle P_{k}^{a}=(I-K_{k}H_{k})P_{k}^{f} & & \displaystyle \text{error covariance correction}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P_{k}^{a}=(I-K_{k}H_{k})P_{k}^{f} & & \displaystyle \text{error covariance correction}.\end{eqnarray}$$
Remark 10.2. The Kalman gain
![]() $K_{k}$
defined in (10.14) can also be expressed as
$K_{k}$
defined in (10.14) can also be expressed as
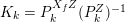 $K_{k}=P_{k}^{X_{f}Z}(P_{k}^{Z})^{-1}$
. Here
$K_{k}=P_{k}^{X_{f}Z}(P_{k}^{Z})^{-1}$
. Here
 $$\begin{eqnarray}P_{k}^{X_{f}Z}=\mathbb{E}[\boldsymbol{X}_{f}^{k}(\boldsymbol{Z}^{k}-H_{k}\boldsymbol{X}_{f}^{k})^{T}]=P_{k}^{f}H_{k}^{T}\end{eqnarray}$$
$$\begin{eqnarray}P_{k}^{X_{f}Z}=\mathbb{E}[\boldsymbol{X}_{f}^{k}(\boldsymbol{Z}^{k}-H_{k}\boldsymbol{X}_{f}^{k})^{T}]=P_{k}^{f}H_{k}^{T}\end{eqnarray}$$
is the cross-covariance between
![]() $\boldsymbol{X}_{f}^{k}$
and the innovation
$\boldsymbol{X}_{f}^{k}$
and the innovation
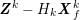 $\boldsymbol{Z}^{k}-H_{k}\boldsymbol{X}_{f}^{k}$
, and
$\boldsymbol{Z}^{k}-H_{k}\boldsymbol{X}_{f}^{k}$
, and
 $$\begin{eqnarray}P_{k}^{Z}=\mathbb{E}[(\boldsymbol{Z}^{k}-H_{k}\boldsymbol{X}_{f}^{k})(\boldsymbol{Z}^{k}-H_{k}\boldsymbol{X}_{f}^{k})^{T}]=H_{k}P_{k}^{f}H_{k}+R_{k}\end{eqnarray}$$
$$\begin{eqnarray}P_{k}^{Z}=\mathbb{E}[(\boldsymbol{Z}^{k}-H_{k}\boldsymbol{X}_{f}^{k})(\boldsymbol{Z}^{k}-H_{k}\boldsymbol{X}_{f}^{k})^{T}]=H_{k}P_{k}^{f}H_{k}+R_{k}\end{eqnarray}$$
is the innovation covariance. Similarly, (10.15e
) can be rewritten as
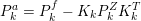 $P_{k}^{a}=P_{k}^{f}-K_{k}P_{k}^{Z}K_{k}^{T}$
. This interpretation is useful when dealing with the unscented Kalman filter (see Section 10.2.3).
$P_{k}^{a}=P_{k}^{f}-K_{k}P_{k}^{Z}K_{k}^{T}$
. This interpretation is useful when dealing with the unscented Kalman filter (see Section 10.2.3).
Remark 10.3. In the linear case, the variational and the sequential approaches yield the same result at the end of a time window, provided the following assumptions are made: the same background estimation and the same covariance matrices are used, and the same measurements are acquired – that is, both algorithms are optimal from a least-squares or minimum variance standpoint.
Let us now return to our problem of estimating the parameter
![]() $\boldsymbol{\unicode[STIX]{x1D703}}$
. We apply the KF algorithm to the system
$\boldsymbol{\unicode[STIX]{x1D703}}$
. We apply the KF algorithm to the system
 $$\begin{eqnarray}\displaystyle \boldsymbol{X}^{k} & = & \displaystyle A_{k-1|k}\boldsymbol{X}^{k-1}+B_{k}\boldsymbol{\unicode[STIX]{x1D703}}^{k}+\boldsymbol{v}^{k},~~k=1,\ldots ,K,\quad \boldsymbol{X}^{0}=\boldsymbol{G},\nonumber\\ \displaystyle \boldsymbol{\unicode[STIX]{x1D703}}^{k} & = & \displaystyle \boldsymbol{\unicode[STIX]{x1D703}}^{k-1}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{X}^{k} & = & \displaystyle A_{k-1|k}\boldsymbol{X}^{k-1}+B_{k}\boldsymbol{\unicode[STIX]{x1D703}}^{k}+\boldsymbol{v}^{k},~~k=1,\ldots ,K,\quad \boldsymbol{X}^{0}=\boldsymbol{G},\nonumber\\ \displaystyle \boldsymbol{\unicode[STIX]{x1D703}}^{k} & = & \displaystyle \boldsymbol{\unicode[STIX]{x1D703}}^{k-1}\nonumber\end{eqnarray}$$
with observations
 $$\begin{eqnarray}\boldsymbol{Z}^{k}=H_{k}\boldsymbol{X}^{k}+\boldsymbol{w}^{k},\quad k=1,\ldots ,K.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{Z}^{k}=H_{k}\boldsymbol{X}^{k}+\boldsymbol{w}^{k},\quad k=1,\ldots ,K.\end{eqnarray}$$
Here
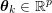 $\boldsymbol{\unicode[STIX]{x1D703}}_{k}\in \mathbb{R}^{p}$
denotes the parameter vector and (under the linearity assumption)
$\boldsymbol{\unicode[STIX]{x1D703}}_{k}\in \mathbb{R}^{p}$
denotes the parameter vector and (under the linearity assumption)
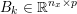 $B_{k}\in \mathbb{R}^{n_{x}\times p}$
, and we assume that no random error is associated with model parameters. This is the so-called state augmentation technique. In order to exploit the KF algorithm, we consider
$B_{k}\in \mathbb{R}^{n_{x}\times p}$
, and we assume that no random error is associated with model parameters. This is the so-called state augmentation technique. In order to exploit the KF algorithm, we consider
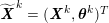 $\widetilde{\boldsymbol{X}}^{k}=(\boldsymbol{X}^{k},\boldsymbol{\unicode[STIX]{x1D703}}^{k})^{T}$
as state vector instead of
$\widetilde{\boldsymbol{X}}^{k}=(\boldsymbol{X}^{k},\boldsymbol{\unicode[STIX]{x1D703}}^{k})^{T}$
as state vector instead of
![]() $\boldsymbol{X}^{k}$
, thus yielding the augmented KF algorithm
$\boldsymbol{X}^{k}$
, thus yielding the augmented KF algorithm
 $$\begin{eqnarray}\displaystyle \widetilde{\boldsymbol{X}}_{f}^{k}=\widetilde{A}_{k-1|k}\widetilde{\boldsymbol{X}}_{a}^{k-1} & & \displaystyle \text{state prediction,}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{\boldsymbol{X}}_{f}^{k}=\widetilde{A}_{k-1|k}\widetilde{\boldsymbol{X}}_{a}^{k-1} & & \displaystyle \text{state prediction,}\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \widetilde{P}_{k}^{f}=\widetilde{A}_{k-1|k}\widetilde{P}_{k-1}^{a}\widetilde{A}_{k-1|k}^{T}+\widetilde{Q}_{k} & & \displaystyle \text{error covariance prediction,}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{P}_{k}^{f}=\widetilde{A}_{k-1|k}\widetilde{P}_{k-1}^{a}\widetilde{A}_{k-1|k}^{T}+\widetilde{Q}_{k} & & \displaystyle \text{error covariance prediction,}\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle K_{k}=\widetilde{P}_{f}^{k}\widetilde{H}_{k}^{T}(\widetilde{H}_{k}\widetilde{P}_{k}^{f}H_{k}^{T}+\widetilde{R}_{k})^{-1} & & \displaystyle \text{Kalman gain evaluation,}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K_{k}=\widetilde{P}_{f}^{k}\widetilde{H}_{k}^{T}(\widetilde{H}_{k}\widetilde{P}_{k}^{f}H_{k}^{T}+\widetilde{R}_{k})^{-1} & & \displaystyle \text{Kalman gain evaluation,}\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \widetilde{\boldsymbol{X}}_{a}^{k}=\widetilde{\boldsymbol{X}}_{f}^{k}+K_{k}(\widetilde{\boldsymbol{Z}}^{k}-\widetilde{H}_{k}\widetilde{\boldsymbol{X}}_{f}^{k}) & & \displaystyle \text{state correction,}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{\boldsymbol{X}}_{a}^{k}=\widetilde{\boldsymbol{X}}_{f}^{k}+K_{k}(\widetilde{\boldsymbol{Z}}^{k}-\widetilde{H}_{k}\widetilde{\boldsymbol{X}}_{f}^{k}) & & \displaystyle \text{state correction,}\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \widetilde{P}_{k}^{a}=(I-K_{k}\widetilde{H}_{k})\widetilde{P}_{k}^{f} & & \displaystyle \text{error covariance correction,}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{P}_{k}^{a}=(I-K_{k}\widetilde{H}_{k})\widetilde{P}_{k}^{f} & & \displaystyle \text{error covariance correction,}\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \widetilde{A}_{k-1|k}=\left[\begin{array}{@{}cc@{}}A_{k-1|k} & B_{k}\\ 0 & I\end{array}\right],\quad \widetilde{\boldsymbol{Z}}^{k}=\left[\begin{array}{@{}c@{}}\boldsymbol{Z}^{k}\\ 0\end{array}\right], & \displaystyle \nonumber\\ \displaystyle & \displaystyle \widetilde{H}_{k}=\left[\begin{array}{@{}cc@{}}H_{k} & 0\\ 0 & 0\end{array}\right],\quad \widetilde{Q}_{k}=\left[\begin{array}{@{}c@{}}Q_{k}\\ 0\end{array}\right],\quad \widetilde{R}_{k}=\left[\begin{array}{@{}cc@{}}R_{k} & 0\\ 0 & 0\end{array}\right]. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \widetilde{A}_{k-1|k}=\left[\begin{array}{@{}cc@{}}A_{k-1|k} & B_{k}\\ 0 & I\end{array}\right],\quad \widetilde{\boldsymbol{Z}}^{k}=\left[\begin{array}{@{}c@{}}\boldsymbol{Z}^{k}\\ 0\end{array}\right], & \displaystyle \nonumber\\ \displaystyle & \displaystyle \widetilde{H}_{k}=\left[\begin{array}{@{}cc@{}}H_{k} & 0\\ 0 & 0\end{array}\right],\quad \widetilde{Q}_{k}=\left[\begin{array}{@{}c@{}}Q_{k}\\ 0\end{array}\right],\quad \widetilde{R}_{k}=\left[\begin{array}{@{}cc@{}}R_{k} & 0\\ 0 & 0\end{array}\right]. & \displaystyle \nonumber\end{eqnarray}$$
We point out that, by construction of the filtering procedure, the estimated parameter values evolve along the simulation period and the actual estimation is achieved with the final values, that is, the estimated parameter vector is
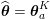 $\widehat{\boldsymbol{\unicode[STIX]{x1D703}}}=\boldsymbol{\unicode[STIX]{x1D703}}_{a}^{K}$
. (Note that in the current formulation
$\widehat{\boldsymbol{\unicode[STIX]{x1D703}}}=\boldsymbol{\unicode[STIX]{x1D703}}_{a}^{K}$
. (Note that in the current formulation
![]() $\unicode[STIX]{x1D703}$
is independent of time.) Hence, we expect these estimation trajectories to fluctuate less and less during the course of the simulation (see e.g. Figure 11.3 in Section 11.3.2); the non-converging case would therefore denote the presence of persistent modelling errors.
$\unicode[STIX]{x1D703}$
is independent of time.) Hence, we expect these estimation trajectories to fluctuate less and less during the course of the simulation (see e.g. Figure 11.3 in Section 11.3.2); the non-converging case would therefore denote the presence of persistent modelling errors.
We conclude this section by pointing out that when a sequential approach like the Kalman filter is used for parameter estimation, the dynamical system has to be solved only once, by updating the parameter value after each assimilation of new measurements. On the other hand, a variational approach would require us to solve the dynamical system on the whole time interval several times, assuming that an iterative approach is used to perform the optimization: see the sketch in Figure 10.1.

Figure 10.1. Variational approach (a) versus Kalman filter (b) approach: in the former, at each optimization stage the whole state dynamics has to be computed, whereas in the latter each measurement is sequentially used for the state (and parameter) correction.
10.2.2 The extended Kalman filter
The classical Kalman filter formulation is well suited to low-dimensional, linear dynamical systems, although in real applications these assumptions are seldom verified. The extended Kalman filter (EKF) was introduced for non-linear dynamical systems, where (10.12) is replaced by
 $$\begin{eqnarray}\boldsymbol{X}^{k}=\mathbf{f}(\boldsymbol{X}^{k-1},\unicode[STIX]{x1D70F}^{k})+\boldsymbol{\unicode[STIX]{x1D700}}^{k},\quad \boldsymbol{Z}^{k}=\mathbf{h}(\boldsymbol{X}^{k},\unicode[STIX]{x1D70F}^{k})+\boldsymbol{\unicode[STIX]{x1D702}}^{k},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{X}^{k}=\mathbf{f}(\boldsymbol{X}^{k-1},\unicode[STIX]{x1D70F}^{k})+\boldsymbol{\unicode[STIX]{x1D700}}^{k},\quad \boldsymbol{Z}^{k}=\mathbf{h}(\boldsymbol{X}^{k},\unicode[STIX]{x1D70F}^{k})+\boldsymbol{\unicode[STIX]{x1D702}}^{k},\end{eqnarray}$$
where
![]() $\mathbf{f}$
and
$\mathbf{f}$
and
![]() $\mathbf{h}$
are two non-linear functions. Non-linearity here involves both the system dynamics and the observation model. The EKF consists in applying the KF algorithm (10.15) to a linearized version of (10.17) around the previous state, so that at each step we set
$\mathbf{h}$
are two non-linear functions. Non-linearity here involves both the system dynamics and the observation model. The EKF consists in applying the KF algorithm (10.15) to a linearized version of (10.17) around the previous state, so that at each step we set
 $$\begin{eqnarray}A_{k-1|k}=\frac{\unicode[STIX]{x2202}\mathbf{f}}{\unicode[STIX]{x2202}\boldsymbol{X}}\biggm\vert_{\boldsymbol{X}_{a}^{k-1},\boldsymbol{\unicode[STIX]{x1D703}}^{k}},\quad H_{k}=\frac{\unicode[STIX]{x2202}\mathbf{h}}{\unicode[STIX]{x2202}\boldsymbol{X}}\biggm\vert_{\boldsymbol{X}_{f}^{k}}.\end{eqnarray}$$
$$\begin{eqnarray}A_{k-1|k}=\frac{\unicode[STIX]{x2202}\mathbf{f}}{\unicode[STIX]{x2202}\boldsymbol{X}}\biggm\vert_{\boldsymbol{X}_{a}^{k-1},\boldsymbol{\unicode[STIX]{x1D703}}^{k}},\quad H_{k}=\frac{\unicode[STIX]{x2202}\mathbf{h}}{\unicode[STIX]{x2202}\boldsymbol{X}}\biggm\vert_{\boldsymbol{X}_{f}^{k}}.\end{eqnarray}$$
At each step two Jacobian matrices have to be evaluated at the current predicted state/parameters. A similar extension of the algorithm (10.16) provides the EKF for parameter estimation. Although feasible in principle, the EKF suffers from several drawbacks. For instance, it entails prohibitive computational costs to invert large matrices and to propagate the covariance matrix in time. Even more importantly, the EKF may lack stability, meaning that as the estimated state deviates from the true state, the linearized model becomes inaccurate, which may lead to an even larger error in state estimation. To mitigate these shortcomings, several strategies have been put in place: low-rank approximation of the covariance matrices have been considered, and other extensions of the original Kalman filter such as the UKF and EnKF have been introduced.
10.2.3 The unscented Kalman filter
While the EKF exploits the differentiation of non-linear operators, modelling both the state dynamics and the observation process, to evaluate the propagation of means and covariances, the unscented Kalman filter (UKF), introduced by Julier, Uhlmann and Durrant-Whyte (Reference Julier, Uhlmann and Durrant-Whyte1995), relies on a set of well-chosen deterministic points (or sigma points) whose propagation via the non-linear operators yields the empirical means and covariances required in the Kalman prediction-correction formulas. The rationale goes by the name of unscented transformation, whose goal is to map a set of points so that their sample distribution approximates the true distribution (Julier, Uhlmann and Durrant-Whyte Reference Julier, Uhlmann and Durrant-Whyte2000).
Supposing that we know the mean
![]() $\mathbb{E}[\boldsymbol{X}]$
and the covariance
$\mathbb{E}[\boldsymbol{X}]$
and the covariance
![]() $\unicode[STIX]{x1D6F4}$
of a random vector
$\unicode[STIX]{x1D6F4}$
of a random vector
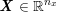 $\boldsymbol{X}\in \mathbb{R}^{n_{x}}$
, the simplest choice is to select
$\boldsymbol{X}\in \mathbb{R}^{n_{x}}$
, the simplest choice is to select
![]() $2n_{x}$
(symmetric) sigma points
$2n_{x}$
(symmetric) sigma points
![]() $x_{(i)}$
as
$x_{(i)}$
as
 $$\begin{eqnarray}x_{(i)}=\mathbb{E}[\boldsymbol{X}]+(\sqrt{n_{x}\unicode[STIX]{x1D6F4}})_{i},\quad x_{(n_{x}+i)}=\mathbb{E}[\boldsymbol{X}]-(\sqrt{n_{x}\unicode[STIX]{x1D6F4}})_{i},\quad i=1,\ldots ,n_{x},\end{eqnarray}$$
$$\begin{eqnarray}x_{(i)}=\mathbb{E}[\boldsymbol{X}]+(\sqrt{n_{x}\unicode[STIX]{x1D6F4}})_{i},\quad x_{(n_{x}+i)}=\mathbb{E}[\boldsymbol{X}]-(\sqrt{n_{x}\unicode[STIX]{x1D6F4}})_{i},\quad i=1,\ldots ,n_{x},\end{eqnarray}$$
where
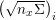 $(\sqrt{n_{x}\unicode[STIX]{x1D6F4}})_{i}$
is the
$(\sqrt{n_{x}\unicode[STIX]{x1D6F4}})_{i}$
is the
![]() $i$
th column of the Cholesky factor of
$i$
th column of the Cholesky factor of
![]() $n_{x}\unicode[STIX]{x1D6F4}$
. Different options for the sigma points selection are however possible: see e.g. Julier and Uhlmann (Reference Julier and Uhlmann2004).
$n_{x}\unicode[STIX]{x1D6F4}$
. Different options for the sigma points selection are however possible: see e.g. Julier and Uhlmann (Reference Julier and Uhlmann2004).
The prediction-correction strategy of the Kalman filter is then performed. Referring to the same notation used in Section 10.2.1 and supposing that the current forecast based on
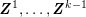 $\boldsymbol{Z}^{1},\ldots ,\boldsymbol{Z}^{k-1}$
is
$\boldsymbol{Z}^{1},\ldots ,\boldsymbol{Z}^{k-1}$
is
![]() $\widehat{\boldsymbol{X}}_{f}^{k}$
, with covariance matrix
$\widehat{\boldsymbol{X}}_{f}^{k}$
, with covariance matrix
![]() $P_{k}^{f}$
, the following correction step is performed.
$P_{k}^{f}$
, the following correction step is performed.
-
∙ From the estimated mean
 $\widehat{\boldsymbol{X}}_{f}^{k}$
and covariance
$\widehat{\boldsymbol{X}}_{f}^{k}$
and covariance
 $P_{k}^{f}$
at time
$P_{k}^{f}$
at time
 $\unicode[STIX]{x1D70F}^{k}$
, select a set of
$\unicode[STIX]{x1D70F}^{k}$
, select a set of
 $2n_{x}$
sigma points centred around
$2n_{x}$
sigma points centred around $$\begin{eqnarray}x_{f,(i)}^{k}=\widehat{\boldsymbol{X}}_{f}^{k}+\Bigl(\sqrt{n_{x}P_{k}^{f}}\Bigr)_{i},~~\,x_{f,(n_{x}+i)}^{k}=\widehat{\boldsymbol{X}}_{f}^{k}-\Bigl(\sqrt{n_{x}P_{k}^{f}}\Bigr)_{i},~~\,i=1,\ldots ,n_{x},\end{eqnarray}$$
$$\begin{eqnarray}x_{f,(i)}^{k}=\widehat{\boldsymbol{X}}_{f}^{k}+\Bigl(\sqrt{n_{x}P_{k}^{f}}\Bigr)_{i},~~\,x_{f,(n_{x}+i)}^{k}=\widehat{\boldsymbol{X}}_{f}^{k}-\Bigl(\sqrt{n_{x}P_{k}^{f}}\Bigr)_{i},~~\,i=1,\ldots ,n_{x},\end{eqnarray}$$
 $\widehat{\boldsymbol{X}}_{f}^{k}$
at a distance given by the standard deviation extracted from the covariance matrix, and obtain the predicted measurement
$\widehat{\boldsymbol{X}}_{f}^{k}$
at a distance given by the standard deviation extracted from the covariance matrix, and obtain the predicted measurement  $$\begin{eqnarray}\widehat{\boldsymbol{Z}}^{k}=\frac{1}{2n_{x}}\mathop{\sum }_{i=1}^{2n_{x}}\widehat{\boldsymbol{Z}}_{(i)}^{k},\quad \text{where }\widehat{\boldsymbol{Z}}_{(i)}^{k}=\mathbf{h}(x_{f,(i)}^{k},\unicode[STIX]{x1D70F}^{k}),\quad i=1,\ldots ,2n_{x}.\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\boldsymbol{Z}}^{k}=\frac{1}{2n_{x}}\mathop{\sum }_{i=1}^{2n_{x}}\widehat{\boldsymbol{Z}}_{(i)}^{k},\quad \text{where }\widehat{\boldsymbol{Z}}_{(i)}^{k}=\mathbf{h}(x_{f,(i)}^{k},\unicode[STIX]{x1D70F}^{k}),\quad i=1,\ldots ,2n_{x}.\end{eqnarray}$$
-
∙ Estimate the covariance of the predicted measurement,
and the cross-covariance between $$\begin{eqnarray}P_{k}^{Z}=\frac{1}{2n_{x}}\mathop{\sum }_{i=1}^{2n_{x}}(\widehat{\boldsymbol{Z}}_{(i)}^{k}-\widehat{\boldsymbol{Z}}^{k})(\widehat{\boldsymbol{Z}}_{(i)}^{k}-\widehat{\boldsymbol{Z}}^{k})^{T}+R_{k},\end{eqnarray}$$
$$\begin{eqnarray}P_{k}^{Z}=\frac{1}{2n_{x}}\mathop{\sum }_{i=1}^{2n_{x}}(\widehat{\boldsymbol{Z}}_{(i)}^{k}-\widehat{\boldsymbol{Z}}^{k})(\widehat{\boldsymbol{Z}}_{(i)}^{k}-\widehat{\boldsymbol{Z}}^{k})^{T}+R_{k},\end{eqnarray}$$
 $\boldsymbol{X}_{f}^{k}$
and
$\boldsymbol{X}_{f}^{k}$
and
 $\widehat{\boldsymbol{Z}}^{k}$
:
$\widehat{\boldsymbol{Z}}^{k}$
:  $$\begin{eqnarray}P_{k}^{X_{f}Z}=\frac{1}{2n_{x}}\mathop{\sum }_{i=1}^{2n_{x}}(\widehat{\boldsymbol{X}}_{f}^{k}-x_{f,(i)}^{k})(\widehat{\boldsymbol{Z}}^{k}-\widehat{\boldsymbol{Z}}_{(i)}^{k})^{T}.\end{eqnarray}$$
$$\begin{eqnarray}P_{k}^{X_{f}Z}=\frac{1}{2n_{x}}\mathop{\sum }_{i=1}^{2n_{x}}(\widehat{\boldsymbol{X}}_{f}^{k}-x_{f,(i)}^{k})(\widehat{\boldsymbol{Z}}^{k}-\widehat{\boldsymbol{Z}}_{(i)}^{k})^{T}.\end{eqnarray}$$
-
∙ Perform the Kalman gain evaluation, state correction and the error covariance correction similarly to (10.16c –10.16e ) (recall Remark 10.2),
 $$\begin{eqnarray}\displaystyle K_{k} & = & \displaystyle P_{k}^{X_{f}Z}(P_{k}^{Z})^{-1},\nonumber\\ \displaystyle \widehat{\boldsymbol{X}}_{a}^{k} & = & \displaystyle \widehat{\boldsymbol{X}}_{f}^{k}+K_{k}(\boldsymbol{Z}^{k}-\widehat{\boldsymbol{Z}}^{k}),\nonumber\\ \displaystyle P_{k}^{a} & = & \displaystyle P_{k}^{f}-K_{k}P_{k}^{Z}K_{k}^{T}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K_{k} & = & \displaystyle P_{k}^{X_{f}Z}(P_{k}^{Z})^{-1},\nonumber\\ \displaystyle \widehat{\boldsymbol{X}}_{a}^{k} & = & \displaystyle \widehat{\boldsymbol{X}}_{f}^{k}+K_{k}(\boldsymbol{Z}^{k}-\widehat{\boldsymbol{Z}}^{k}),\nonumber\\ \displaystyle P_{k}^{a} & = & \displaystyle P_{k}^{f}-K_{k}P_{k}^{Z}K_{k}^{T}.\nonumber\end{eqnarray}$$
In the prediction step, a set of sigma points is selected as
 $$\begin{eqnarray}x_{a,(i)}^{k}=\widehat{\boldsymbol{X}}_{a}^{k}+(\sqrt{n_{x}P_{k}^{a}})_{i},\quad x_{a,(n_{x}+i)}^{k}=\widehat{\boldsymbol{X}}_{a}^{k}-(\sqrt{n_{x}P_{k}^{a}})_{i},\quad i=1,\ldots ,n_{x}\end{eqnarray}$$
$$\begin{eqnarray}x_{a,(i)}^{k}=\widehat{\boldsymbol{X}}_{a}^{k}+(\sqrt{n_{x}P_{k}^{a}})_{i},\quad x_{a,(n_{x}+i)}^{k}=\widehat{\boldsymbol{X}}_{a}^{k}-(\sqrt{n_{x}P_{k}^{a}})_{i},\quad i=1,\ldots ,n_{x}\end{eqnarray}$$
and a forward computation of one time window is performed to get the state prediction at step
![]() $k+1$
:
$k+1$
:
 $$\begin{eqnarray}\widehat{\boldsymbol{X}}_{f}^{k+1}=\frac{1}{2n_{x}}\mathop{\sum }_{i=1}^{2n_{x}}x_{f,(i)}^{k+1},\quad \text{where }x_{f,(i)}^{k+1}=\mathbf{f}(x_{a,(i)}^{k},\unicode[STIX]{x1D70F}^{k+1})\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\boldsymbol{X}}_{f}^{k+1}=\frac{1}{2n_{x}}\mathop{\sum }_{i=1}^{2n_{x}}x_{f,(i)}^{k+1},\quad \text{where }x_{f,(i)}^{k+1}=\mathbf{f}(x_{a,(i)}^{k},\unicode[STIX]{x1D70F}^{k+1})\end{eqnarray}$$
(note that each sigma point is treated independently). Finally, the covariance is updated as
 $$\begin{eqnarray}P_{k+1}^{f}=\frac{1}{2n_{x}}\mathop{\sum }_{i=1}^{2n_{x}}(\widehat{\boldsymbol{X}}_{f}^{k+1}-x_{f,(i+1)}^{k})(\widehat{\boldsymbol{X}}_{f}^{k+1}-x_{f,(i+1)}^{k})^{T}+Q_{k+1}.\end{eqnarray}$$
$$\begin{eqnarray}P_{k+1}^{f}=\frac{1}{2n_{x}}\mathop{\sum }_{i=1}^{2n_{x}}(\widehat{\boldsymbol{X}}_{f}^{k+1}-x_{f,(i+1)}^{k})(\widehat{\boldsymbol{X}}_{f}^{k+1}-x_{f,(i+1)}^{k})^{T}+Q_{k+1}.\end{eqnarray}$$
Provided the analysis step is performed in parallel, the cost of the whole estimation procedure is comparable to that of a simple forward simulation. By contrast, a variational estimation would require a significant number of successive iterations (typically, of the order of hundreds) of both forward and adjoint simulations.
An augmented formulation of the UKF can be easily obtained, similarly to (10.16), in order to treat the case where the system depends on a set of
![]() $p$
parameters affected by uncertainty, which need to be estimated. Nevertheless, the very large dimension of the state vector (depending on the spatial discretization of the state variable) makes this filter intractable in practice. In those cases where uncertainty only affects the parameters, and
$p$
parameters affected by uncertainty, which need to be estimated. Nevertheless, the very large dimension of the state vector (depending on the spatial discretization of the state variable) makes this filter intractable in practice. In those cases where uncertainty only affects the parameters, and
![]() $p\ll n_{x}$
, a much more feasible version yielding a reduced-order UKF limits the computations of the filter operator to a subspace of small dimension and is much more efficient. The reduction to the parametric space as regarding the choice of the sigma-points for the sake of parameter estimation was originally introduced by Pham (Reference Pham2001) and Hoteit, Pham and Blum (Reference Hoteit, Pham and Blum2002); an initial application to the estimation of electrophysiology parameters can be found in Wang et al. (Reference Wang, Zhang, Wong and Shi2009) and Wang et al. (Reference Wang, Wong, Zhang, Liu and Shi2011). A detailed analysis of the reduced-order UKF can be found in Moireau and Chapelle (Reference Moireau and Chapelle2011), for example. A possible alternative, recently explored by Pagani, Manzoni and Quarteroni (Reference Pagani, Manzoni and Quarteroni2016) and Pagani (Reference Pagani2016), is to perform a state reduction (rather than a reduction of the parameter space) relying on a reduced-order model, and then consider the problem of simultaneous state/parameter estimation.
$p\ll n_{x}$
, a much more feasible version yielding a reduced-order UKF limits the computations of the filter operator to a subspace of small dimension and is much more efficient. The reduction to the parametric space as regarding the choice of the sigma-points for the sake of parameter estimation was originally introduced by Pham (Reference Pham2001) and Hoteit, Pham and Blum (Reference Hoteit, Pham and Blum2002); an initial application to the estimation of electrophysiology parameters can be found in Wang et al. (Reference Wang, Zhang, Wong and Shi2009) and Wang et al. (Reference Wang, Wong, Zhang, Liu and Shi2011). A detailed analysis of the reduced-order UKF can be found in Moireau and Chapelle (Reference Moireau and Chapelle2011), for example. A possible alternative, recently explored by Pagani, Manzoni and Quarteroni (Reference Pagani, Manzoni and Quarteroni2016) and Pagani (Reference Pagani2016), is to perform a state reduction (rather than a reduction of the parameter space) relying on a reduced-order model, and then consider the problem of simultaneous state/parameter estimation.
10.3 Applications to cardiovascular modelling
In the past decade, parameter identification problems have been considered in several applications to cardiovascular modelling. In this section we report a list of relevant contributions; two substantive examples will be more specifically discussed in Sections 10.3.1 and 10.3.2.
The problem of identifying a set of parameters of one-dimensional models for the arterial circulation was first considered by Martin et al. (Reference Martin, Clément, Decoene and Gerbeau2005), who considered a non-linear least-squares approach based on the optimization of a cost function and the introduction of a suitable adjoint problem. A relevant application in this context is the estimation of the elastic coefficient of a subject-specific vessel based on measurements of its displacement recovered from medical images. A variational approach based on the minimization of suitable functionals has been proposed by Perego, Veneziani and Vergara (Reference Perego, Veneziani and Vergara2011) and, more recently, by Bertagna and Veneziani (Reference Bertagna and Veneziani2014); we present this technique in Section 10.3.1. A different approach based on an unscented Kalman filter has been proposed by Bertoglio et al. (Reference Bertoglio, Moireau and Gerbeau2012) and further explored by Moireau et al. (Reference Moireau, Bertoglio, Xiao, Figueroa, Taylor, Chapelle and Gerbeau2013) to estimate modelling parameters pertaining to vessel wall boundary conditions. Similar strategies based on the unscented Kalman filter have been considered by Lombardi (Reference Lombardi2014), for example, to solve inverse problems in large one-dimensional arterial networks, and by Pant, Fabrèges, Gerbeau and Vignon-Clementel (Reference Pant, Fabrèges, Gerbeau and Vignon-Clementel2014) to estimate lumped (e.g. windkessel) model parameters by using the pressure curve in the ascending aorta.
Other approaches have been considered, for example in Blanco, Watanabe and Feijóo (Reference Blanco, Watanabe and Feijóo2012), to characterize the terminal peripheral resistances in a network describing one-dimensional arterial blood flow, or in Spilker and Taylor (Reference Spilker and Taylor2010) to adjust the parameters of windkessel outflow boundary conditions of three-dimensional blood flow models, in order to match some desired features of pressure and flow waveforms.
Several recent works have focused on parameter identification and, more generally speaking, on the solution of inverse problems in heart modelling. The classical inverse problem in electrocardiology has been considered by many authors in the past few decades. It consists in recovering the electrical potential at the epicardial surface by using a number of remote, non-invasive or minimally invasive potential recordings, such as those acquired along the body surface (Rudy and Messinger-Rapport Reference Rudy and Messinger-Rapport1988, Pullan et al. Reference Pullan, Cheng, Nash, Bradley and Paterson2001, Cheng, Bodley and Pullan Reference Cheng, Bodley and Pullan2003), usually referred to as body surface-potential data. In its original formulation, this problem involves the pure (linear) diffusion model for the torso as a direct problem (Colli Franzone, Taccardi and Viganotti Reference Colli Franzone, Taccardi and Viganotti1978, Colli Franzone, Guerri, Viganotti and Taccardi Reference Colli Franzone, Guerri, Viganotti and Taccardi1985, Yamashita Reference Yamashita1982): see Section 7.1.5. This inverse problem is mathematically ill-posed, and several regularization strategies have been proposed; see e.g. the reviews by Pullan et al. (Reference Pullan, Cheng, Nash, Ghodrati, Macleod, Brooks and Macfarlane2010) and Colli Franzone et al. (Reference Colli Franzone, Pavarino and Scacchi2014). Another method to solve the inverse electrocardiology problem relies on measurements of the electrical potential within one of the heart chambers (ventricles and atria) by means of non-contact multi-electrode catheter arrays, and tries to estimate the endocardial surface potential from them. Since the measurements are recorded closer to the endocardial surface than those acquired on the body surface, this problem is less ill-conditioned than the former. If the problem is recast in the form of a parameter estimation problem, that is, where the epicardial potential distribution is described in terms of a set of parameters, the inverse problem can be more easily tackled.
More generally speaking, inverse and parameter estimation problems have been considered in several works in order to approximately reconstruct the cardiac electrical activity in the myocardium, for example, and to provide indications of the presence of ischaemic or infarcted zones by estimating conductibility parameters. Concerning variational approaches, we can mention a level set framework for identifying heart infarctions (Lykaser and Nielsen Reference Lykaser and Nielsen2006) by relying on a least-squares formulation and an adjoint problem to determine the gradient of the cost functional. In this case, the infarcted region in a simplified two-dimensional domain has been described in terms of a discrete level set function, involving a set of parameters to be identified from synthetic ECG boundary measurements, and a Tikhonov regularization procedure. MacLachlan et al. (Reference Maclachlan, Nielsen, Lysaker and Tveito2006) and Nielsen et al. (Reference Nielsen, Cai and Lykaser2007a ) considered the solution of a parameter identification problem to locate (in terms of size and position) ischaemic regions, where a simplified state elliptic system models the electrical potential in both the heart and the torso in the resting phase. In all these papers, the PDE-constrained optimization problem was solved using an iterative method, following an optimize-then-discretize approach. Nielsen, Lykaser and Tveito (Reference Nielsen, Lykaser and Tveito2007b ) instead considered an all-at-once approach for a similar problem, also taking into account anisotropic cardiac conductivities and fibre orientation. A more involved version of this problem, still focusing on the inverse electrocardiographic source localization of ischaemias, has been considered more recently by Wang et al. (Reference Wang, Kirby, Macleod and Johnson2013).
The personalization of an eikonal model, via the identification of local conduction velocities and parameters related to the action potential duration restitution curve, has been addressed by Chinchapatnam et al. (Reference Chinchapatnam, Rhode, Ginks, Rinaldi, Lambiase, Razavi, Arridge and Sermesant2008) and Relan et al. (Reference Relan, Chinchapatnam, Sermesant, Rhode, Ginks, Delingette, Rinaldi, Razavi and Ayache2011). More recently, Yang and Veneziani (Reference Yang and Veneziani2015) proposed a variational approach for the estimation of cardiac conductivities in a bidomain model, from measurements of the trans-membrane and extracellular potentials available at some locations in the tissue. Boulakia et al. (Reference Boulakia, Fernández, Gerbeau and Zemzemi2008) have considered parameter estimation in a problem where the bidomain model for the heart is coupled with the Laplace equation for the passive conduction in the torso, in order to estimate the torso conductivity parameters.
The unscented Kalman filter was exploited by Wang et al. (Reference Wang, Wong, Zhang, Liu and Shi2011) and by Marchesseau et al. (Reference Marchesseau, Delingette, Sermesant, Cabrera-Lozoya, Tobon-Gomez, Moireau, Figueras i Ventura, Lekadir, Hernandez, Garreau, Donal, Leclercq, Duckett, Rhode, Rinaldi, Frangi, Razavi, Chapelle and Ayache2013) and Talbot et al. (Reference Talbot, Cotin, Razavi, Rinaldi and Delingette2015) to identify scar locations and their size from body surface-potential and MRI data, using a monodomain two-variable Aliev–Panfilov model. A reduced-order UKF was used by Corrado, Gerbeau and Moireau (Reference Corrado, Gerbeau and Moireau2015) to estimate electrical parameters within a coupled electromechanical model, by taking advantage of observations from both electrocardiograms and myocardium displacements.
Another inverse problem in electrophysiology has been studied by Vergara et al. (Reference Vergara, Palamara, Catanzariti, Nobile, Faggiano, Pangrazzi, Centonze, Maines, Quarteroni and Vergara2014) and Palamara et al. (Reference Palamara, Vergara, Faggiano and Nobile2015). Measurements of the electrical activation time on the endocardium, acquired via NavX (see Section 6.2), were used to find the optimal Purkinje network configuration. For this problem, the parameters to be estimated are the coordinates of the network. In particular, starting from an initial network with a fractal shape, a functional accounting for the discrepancy between measured and computed activation times is minimized to find the patient-specific location of the Purkinje muscle junctions (see Section 5.3). This methodology has been successfully applied to real pathological scenarios: see Palamara et al. (Reference Palamara, Vergara, Catanzariti, Faggiano, Centonze, Pangrazzi, Maines and Quarteroni2014).
Regarding cardiac biomechanics, Moireau, Chapelle and Le Tallec (Reference Moireau, Chapelle and Le2009) and Moireau and Chapelle (Reference Moireau and Chapelle2011) addressed the estimation of contractility parameters using the unscented Kalman filter, where the degree of damage in cardiac tissues caused by an infarct is estimated using velocity measurements from tagged MRI; see also Moireau, Chapelle and Le Tallec (Reference Moireau, Chapelle and Le2008). A reduced-order UKF was used by Xi et al. (Reference Xi, Lamata, Lee, Moireau, Chapelle and Smith2011) to identify material parameters in a transversally isotropic mechanical model; further details concerning this application will be provided in Section 10.3.2. Subsequently, the same technique was exploited by Chabiniok et al. (Reference Chabiniok, Moireau, Lesault, Rahmouni, Deux and Chapelle2012) to estimate contractility values in a more complex cardiac model, where the tissue is described by combining an active constitutive law in the muscle fibre direction and a visco-hyperelastic material, using actual clinical data consisting of in vivo cine-MRI image sequences and pressure measurements.
Finally, for the coupled electromechanical problem, very few numerical results are now available. The personalization of a 3D electromechanical model has been tackled by variational approaches, for example by Sermesant et al. (Reference Sermesant, Moireau, Camara, Sainte-Marie, Andriantsimiavona, Cimrman, Hill, Chapelle and Razavi2006), who estimated local ventricular myocardium contractility using MRI in an electromechanical model. Similarly, Delingette et al. (Reference Delingette, Billet, Wong, Sermesant, Rhode, Ginks, Rinaldi, Razavi and Ayache2012) estimated both the parameters of a Mitchell–Schaeffer model and cardiac contractilities from catheterized electrophysiology data and cine-MRI images, respectively. Marchesseau et al. (Reference Marchesseau, Delingette, Sermesant and Ayache2012) performed the calibration of mechanical parameters of a complete electromechanical model of the heart involving the eikonal model for electrophysiology and an isotropic Mooney–Rivlin material model for cardiac mechanics, relying on the unscented Kalman filter.
Although several works have made a big step forward, the solution of parameter estimation problems remains an open computational challenge if complex, coupled models and patient-specific data are taken into account. Further, when UKF and EnKF techniques are exploited – which exhibit natural parallelism to a high degree – the need to evaluate the state dynamics for several different scenarios (given by the elements of the ensemble, for example) makes the computational effort exorbitant. For this reason, simplified physical models have been considered in many contexts; on the other hand, reduced-order strategies, such as the reduced-order unscented Kalman filter, have recently been proposed as a possible way to overcome the computational complexity arising from these problems. Dramatic progress is expected in this field in the next few years.
10.3.1 A variational approach for estimating the tissue compliance
In this section we illustrate a variational approach introduced by Perego et al. (Reference Perego, Veneziani and Vergara2011) to estimate the Young’s modulus
![]() $E$
of a cardiovascular tissue from displacement data. Indeed, this parameter – and, more generally speaking, the deformability of a soft tissue – is an important index for detecting diseases: low compliance may indicate atherosclerosis or hypertension in the case of an artery, or a marker of diastolic dysfunction in the case of the left ventricle wall. The basic steps are (i) to retrieve the vessel displacement
$E$
of a cardiovascular tissue from displacement data. Indeed, this parameter – and, more generally speaking, the deformability of a soft tissue – is an important index for detecting diseases: low compliance may indicate atherosclerosis or hypertension in the case of an artery, or a marker of diastolic dysfunction in the case of the left ventricle wall. The basic steps are (i) to retrieve the vessel displacement
![]() $\boldsymbol{d}_{\mathit{meas}}$
by image registration procedures on time frames of the vessel of interest, and then (ii) to minimize the difference between
$\boldsymbol{d}_{\mathit{meas}}$
by image registration procedures on time frames of the vessel of interest, and then (ii) to minimize the difference between
![]() $\boldsymbol{d}_{\mathit{meas}}$
and the displacement computed by solving the coupled 3D blood vessel problem, in order to estimate Young’s modulus. Here the structure is assumed to be linearly elastic, and the only parameter to be estimated is
$\boldsymbol{d}_{\mathit{meas}}$
and the displacement computed by solving the coupled 3D blood vessel problem, in order to estimate Young’s modulus. Here the structure is assumed to be linearly elastic, and the only parameter to be estimated is
![]() $E$
, which is generally a function of space (e.g. an atherosclerotic plaque has a different modulus to healthy tissue) but not of time.
$E$
, which is generally a function of space (e.g. an atherosclerotic plaque has a different modulus to healthy tissue) but not of time.
The former step consists of data acquisition, image segmentation and reconstruction, and finally registration; see Perego et al. (Reference Perego, Veneziani and Vergara2011) for further details. The latter, which we will address, is an example of an inverse fluid–structure interaction (IFSI) problem, and results in a constrained optimization problem, where the constraint is the FSI problem and the functional to be minimized is a measure of the mismatch between the data and the computed solution.
An initial formulation of the IFSI problem is obtained by assuming that the displacement data
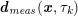 $\boldsymbol{d}_{\mathit{meas}}(\boldsymbol{x},\unicode[STIX]{x1D70F}_{k})$
for
$\boldsymbol{d}_{\mathit{meas}}(\boldsymbol{x},\unicode[STIX]{x1D70F}_{k})$
for
![]() $\boldsymbol{x}\in \unicode[STIX]{x1D6F4}^{\unicode[STIX]{x1D70F}_{k}}$
retrieved from the image registration process are available within the interval
$\boldsymbol{x}\in \unicode[STIX]{x1D6F4}^{\unicode[STIX]{x1D70F}_{k}}$
retrieved from the image registration process are available within the interval
![]() $[0,T]$
in some instants denoted by
$[0,T]$
in some instants denoted by
![]() $\unicode[STIX]{x1D70F}^{k}$
,
$\unicode[STIX]{x1D70F}^{k}$
,
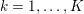 $k=1,\ldots ,K$
. Here
$k=1,\ldots ,K$
. Here
![]() $K$
is the number of instants when image registration is performed,
$K$
is the number of instants when image registration is performed,
![]() $\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D70F}$
is the time step between two measurements, driven by the sampling frequency of the image devices, and
$\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D70F}$
is the time step between two measurements, driven by the sampling frequency of the image devices, and
![]() $\unicode[STIX]{x1D6F4}^{\unicode[STIX]{x1D70F}_{k}}$
denotes the interface between the fluid and the structure domain. Following the formulation of problem (10.4), we consider the functional
$\unicode[STIX]{x1D6F4}^{\unicode[STIX]{x1D70F}_{k}}$
denotes the interface between the fluid and the structure domain. Following the formulation of problem (10.4), we consider the functional
 $$\begin{eqnarray}\displaystyle {\mathcal{J}}_{K}(\boldsymbol{d},E) & = & \displaystyle \frac{1}{2}\mathop{\sum }_{k=1}^{K}~\int _{\unicode[STIX]{x1D6F4}^{\unicode[STIX]{x1D70F}_{k}}}(\boldsymbol{d}_{\mathit{meas}}(\boldsymbol{x},\unicode[STIX]{x1D70F}^{k})-\boldsymbol{d}(\boldsymbol{x},\unicode[STIX]{x1D70F}^{k}))^{2}\text{d}\unicode[STIX]{x1D70E}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D6FC}_{E}}{2}\mathop{\sum }_{k=1}^{K}\,\int _{\unicode[STIX]{x1D6FA}_{s}}(E(\boldsymbol{x},\unicode[STIX]{x1D70F}^{k})-E_{\mathit{ref}})^{2}\text{d}\boldsymbol{x},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{J}}_{K}(\boldsymbol{d},E) & = & \displaystyle \frac{1}{2}\mathop{\sum }_{k=1}^{K}~\int _{\unicode[STIX]{x1D6F4}^{\unicode[STIX]{x1D70F}_{k}}}(\boldsymbol{d}_{\mathit{meas}}(\boldsymbol{x},\unicode[STIX]{x1D70F}^{k})-\boldsymbol{d}(\boldsymbol{x},\unicode[STIX]{x1D70F}^{k}))^{2}\text{d}\unicode[STIX]{x1D70E}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D6FC}_{E}}{2}\mathop{\sum }_{k=1}^{K}\,\int _{\unicode[STIX]{x1D6FA}_{s}}(E(\boldsymbol{x},\unicode[STIX]{x1D70F}^{k})-E_{\mathit{ref}})^{2}\text{d}\boldsymbol{x},\end{eqnarray}$$
where
 $\boldsymbol{d}(\boldsymbol{x},\unicode[STIX]{x1D70F}^{k})$
denotes the solution of the FSI system (4.44) in the ALE formulation, at
$\boldsymbol{d}(\boldsymbol{x},\unicode[STIX]{x1D70F}^{k})$
denotes the solution of the FSI system (4.44) in the ALE formulation, at
![]() $t=\unicode[STIX]{x1D70F}^{k}$
and the second term is a non-negative Tikhonov regularization term. Here
$t=\unicode[STIX]{x1D70F}^{k}$
and the second term is a non-negative Tikhonov regularization term. Here
![]() $E_{\mathit{ref}}$
is a prior estimate (available from ex vivo specimens, for example), so that the regularization forces
$E_{\mathit{ref}}$
is a prior estimate (available from ex vivo specimens, for example), so that the regularization forces
![]() $E$
to be close to its reference value. Given an admissible set
$E$
to be close to its reference value. Given an admissible set
![]() ${\mathcal{E}}_{ad}$
where we seek the parameter
${\mathcal{E}}_{ad}$
where we seek the parameter
![]() $E$
, a possible formulation of the IFSI problem reads as follows. For
$E$
, a possible formulation of the IFSI problem reads as follows. For
 $t>0,\boldsymbol{x}\in \unicode[STIX]{x1D6FA}_{s}$
, find
$t>0,\boldsymbol{x}\in \unicode[STIX]{x1D6FA}_{s}$
, find
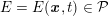 $E=E(\boldsymbol{x},t)\in {\mathcal{P}}$
that minimizes (10.18) under the constraint (4.44). A possible choice for
$E=E(\boldsymbol{x},t)\in {\mathcal{P}}$
that minimizes (10.18) under the constraint (4.44). A possible choice for
![]() ${\mathcal{P}}$
is
${\mathcal{P}}$
is
 $$\begin{eqnarray}{\mathcal{P}}=\{E:E\in L^{\infty }(\unicode[STIX]{x1D6FA}_{s}),\,0<E_{\min }\leq E\leq E_{\max },\text{with }E_{\min },E_{\max }\in \mathbb{R}\}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{P}}=\{E:E\in L^{\infty }(\unicode[STIX]{x1D6FA}_{s}),\,0<E_{\min }\leq E\leq E_{\max },\text{with }E_{\min },E_{\max }\in \mathbb{R}\}.\end{eqnarray}$$
Such a problem entails the solution of a time-dependent minimization problem, for which a classical KKT system can be obtained using the Lagrange multiplier method. In this setting the parameter
![]() $E$
plays the role of the control variable. However, this approach is rather involved, since the adjoint problem results in a final value problem which would involve differentiation with respect to the deformable domain as well: the so-called shape derivative. Moreover, it requires a massive memory occupancy as the solution at all the time steps needs to be stored due to the back-in-time nature of the adjoint problem.
$E$
plays the role of the control variable. However, this approach is rather involved, since the adjoint problem results in a final value problem which would involve differentiation with respect to the deformable domain as well: the so-called shape derivative. Moreover, it requires a massive memory occupancy as the solution at all the time steps needs to be stored due to the back-in-time nature of the adjoint problem.
A more convenient alternative numerical approach proposed by Perego et al. (Reference Perego, Veneziani and Vergara2011) first considers the time-discretization of the forward problem, and formulates a minimization problem at each time step. For simplicity a constant time step
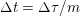 $\unicode[STIX]{x1D6E5}t=\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D70F}/m$
is assumed, for a suitable
$\unicode[STIX]{x1D6E5}t=\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D70F}/m$
is assumed, for a suitable
![]() $m\in \mathbb{N}$
,
$m\in \mathbb{N}$
,
![]() $m\geq 1$
, that is, the instants
$m\geq 1$
, that is, the instants
![]() $\unicode[STIX]{x1D70F}^{k}$
in which measurements are acquired are a subset of the time discretization of (4.44); for simplicity, we will consider
$\unicode[STIX]{x1D70F}^{k}$
in which measurements are acquired are a subset of the time discretization of (4.44); for simplicity, we will consider
![]() $m=1$
. For the time discretization of (4.44), we consider implicit methods with a semi-implicit treatment of the convective term and of the fluid domain, whereas the fluid viscous term is treated implicitly. As in Section 4.6.1, we use the superscript
$m=1$
. For the time discretization of (4.44), we consider implicit methods with a semi-implicit treatment of the convective term and of the fluid domain, whereas the fluid viscous term is treated implicitly. As in Section 4.6.1, we use the superscript
![]() $\ast$
to identify fluid quantities extrapolated from corresponding quantities at previous time steps. Moreover, we introduce the spaces
$\ast$
to identify fluid quantities extrapolated from corresponding quantities at previous time steps. Moreover, we introduce the spaces
 $$\begin{eqnarray}\displaystyle & \boldsymbol{V}^{\ast }=\{\boldsymbol{v}\in \boldsymbol{H}^{1}(\unicode[STIX]{x1D6FA}_{f}^{\ast }):\,\boldsymbol{v}|_{\unicode[STIX]{x1D6E4}_{D,f}^{\ast }}=\mathbf{0}\},\quad Q^{\ast }=L^{2}(\unicode[STIX]{x1D6FA}_{f}^{\ast }), & \displaystyle \nonumber\\ \displaystyle & \boldsymbol{W}=\{\boldsymbol{\unicode[STIX]{x1D713}}\in \boldsymbol{H}^{1}(\unicode[STIX]{x1D6FA}_{s}):\,\boldsymbol{\unicode[STIX]{x1D713}}_{\unicode[STIX]{x1D6E4}_{D,s}}=\mathbf{0}\}, & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \boldsymbol{V}^{\ast }=\{\boldsymbol{v}\in \boldsymbol{H}^{1}(\unicode[STIX]{x1D6FA}_{f}^{\ast }):\,\boldsymbol{v}|_{\unicode[STIX]{x1D6E4}_{D,f}^{\ast }}=\mathbf{0}\},\quad Q^{\ast }=L^{2}(\unicode[STIX]{x1D6FA}_{f}^{\ast }), & \displaystyle \nonumber\\ \displaystyle & \boldsymbol{W}=\{\boldsymbol{\unicode[STIX]{x1D713}}\in \boldsymbol{H}^{1}(\unicode[STIX]{x1D6FA}_{s}):\,\boldsymbol{\unicode[STIX]{x1D713}}_{\unicode[STIX]{x1D6E4}_{D,s}}=\mathbf{0}\}, & \displaystyle \nonumber\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6E4}_{D,f}^{\ast }$
and
$\unicode[STIX]{x1D6E4}_{D,f}^{\ast }$
and
![]() $\unicode[STIX]{x1D6E4}_{D,s}$
are the portions of the boundary where a Dirichlet condition is prescribed. Further, we let
$\unicode[STIX]{x1D6E4}_{D,s}$
are the portions of the boundary where a Dirichlet condition is prescribed. Further, we let
 $$\begin{eqnarray}\boldsymbol{Z}^{\ast }=\{(\boldsymbol{v},\boldsymbol{\unicode[STIX]{x1D713}})\in \boldsymbol{V}^{\ast }\times \boldsymbol{W}:\,\boldsymbol{v}|_{\unicode[STIX]{x1D6F4}^{\ast }}-\widehat{\boldsymbol{\unicode[STIX]{x1D713}}}|_{\unicode[STIX]{x1D6F4}^{\ast }}/\unicode[STIX]{x1D6E5}t=\mathbf{0}\},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{Z}^{\ast }=\{(\boldsymbol{v},\boldsymbol{\unicode[STIX]{x1D713}})\in \boldsymbol{V}^{\ast }\times \boldsymbol{W}:\,\boldsymbol{v}|_{\unicode[STIX]{x1D6F4}^{\ast }}-\widehat{\boldsymbol{\unicode[STIX]{x1D713}}}|_{\unicode[STIX]{x1D6F4}^{\ast }}/\unicode[STIX]{x1D6E5}t=\mathbf{0}\},\end{eqnarray}$$
and introduce the following bilinear forms:
 $$\begin{eqnarray}\displaystyle a(\boldsymbol{v},\boldsymbol{d};\boldsymbol{w},\boldsymbol{\unicode[STIX]{x1D713}})^{\ast } & = & \displaystyle \frac{\unicode[STIX]{x1D70C}_{f}}{\unicode[STIX]{x1D6E5}t}(\boldsymbol{v},\boldsymbol{w})_{f}^{\ast }+(\boldsymbol{T}_{f}(\boldsymbol{v},p),\unicode[STIX]{x1D6FB}\boldsymbol{w})_{f}^{\ast }\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D70C}_{f}(((\boldsymbol{v}^{\ast }-\boldsymbol{v}_{f}^{\ast })\cdot \unicode[STIX]{x1D6FB})\boldsymbol{v},\boldsymbol{w})_{f}^{\ast }+\unicode[STIX]{x1D70C}_{s}\biggl(\frac{\boldsymbol{d}}{\unicode[STIX]{x1D6E5}t^{2}},\frac{\boldsymbol{\unicode[STIX]{x1D713}}}{\unicode[STIX]{x1D6E5}t}\biggr)_{s},\nonumber\\ \displaystyle b(q;\boldsymbol{w})^{\ast } & = & \displaystyle -(q,\unicode[STIX]{x1D6FB}\cdot \boldsymbol{w})_{f}^{\ast },\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle a(\boldsymbol{v},\boldsymbol{d};\boldsymbol{w},\boldsymbol{\unicode[STIX]{x1D713}})^{\ast } & = & \displaystyle \frac{\unicode[STIX]{x1D70C}_{f}}{\unicode[STIX]{x1D6E5}t}(\boldsymbol{v},\boldsymbol{w})_{f}^{\ast }+(\boldsymbol{T}_{f}(\boldsymbol{v},p),\unicode[STIX]{x1D6FB}\boldsymbol{w})_{f}^{\ast }\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D70C}_{f}(((\boldsymbol{v}^{\ast }-\boldsymbol{v}_{f}^{\ast })\cdot \unicode[STIX]{x1D6FB})\boldsymbol{v},\boldsymbol{w})_{f}^{\ast }+\unicode[STIX]{x1D70C}_{s}\biggl(\frac{\boldsymbol{d}}{\unicode[STIX]{x1D6E5}t^{2}},\frac{\boldsymbol{\unicode[STIX]{x1D713}}}{\unicode[STIX]{x1D6E5}t}\biggr)_{s},\nonumber\\ \displaystyle b(q;\boldsymbol{w})^{\ast } & = & \displaystyle -(q,\unicode[STIX]{x1D6FB}\cdot \boldsymbol{w})_{f}^{\ast },\nonumber\end{eqnarray}$$
where
 $$\begin{eqnarray}(\boldsymbol{v},\boldsymbol{w})_{f}^{\ast }=\int _{\unicode[STIX]{x1D6FA}_{f}^{\ast }}\boldsymbol{v}\cdot \boldsymbol{w}\text{d}\boldsymbol{x}\quad \text{and}\quad (\boldsymbol{\unicode[STIX]{x1D713}},\boldsymbol{\unicode[STIX]{x1D712}})_{s}=\int _{\unicode[STIX]{x1D6FA}_{s}}\boldsymbol{\unicode[STIX]{x1D713}}\cdot \boldsymbol{\unicode[STIX]{x1D712}}\text{d}\boldsymbol{x}.\end{eqnarray}$$
$$\begin{eqnarray}(\boldsymbol{v},\boldsymbol{w})_{f}^{\ast }=\int _{\unicode[STIX]{x1D6FA}_{f}^{\ast }}\boldsymbol{v}\cdot \boldsymbol{w}\text{d}\boldsymbol{x}\quad \text{and}\quad (\boldsymbol{\unicode[STIX]{x1D713}},\boldsymbol{\unicode[STIX]{x1D712}})_{s}=\int _{\unicode[STIX]{x1D6FA}_{s}}\boldsymbol{\unicode[STIX]{x1D713}}\cdot \boldsymbol{\unicode[STIX]{x1D712}}\text{d}\boldsymbol{x}.\end{eqnarray}$$
Then, for any given
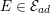 $E\in {\mathcal{E}}_{ad}$
, at each time
$E\in {\mathcal{E}}_{ad}$
, at each time
![]() $t^{n+1}$
, the time-discretized forward FSI problem consists of the following steps.
$t^{n+1}$
, the time-discretized forward FSI problem consists of the following steps.
-
(1) Compute extrapolations
 $\unicode[STIX]{x1D6FA}_{f}^{\ast },\,\boldsymbol{v}^{\ast }$
and
$\unicode[STIX]{x1D6FA}_{f}^{\ast },\,\boldsymbol{v}^{\ast }$
and
 $\boldsymbol{v}_{f}^{\ast }$
to approximate
$\boldsymbol{v}_{f}^{\ast }$
to approximate
 $\unicode[STIX]{x1D6FA}_{f}^{n+1},\,\boldsymbol{v}^{n+1}$
and
$\unicode[STIX]{x1D6FA}_{f}^{n+1},\,\boldsymbol{v}^{n+1}$
and
 $\boldsymbol{v}_{f}^{n+1}$
.
$\boldsymbol{v}_{f}^{n+1}$
. -
(2) Given
 $\boldsymbol{f}_{f}^{n+1}\in \boldsymbol{L}^{2}(\unicode[STIX]{x1D6FA}_{f}^{\ast })$
and
$\boldsymbol{f}_{f}^{n+1}\in \boldsymbol{L}^{2}(\unicode[STIX]{x1D6FA}_{f}^{\ast })$
and
 $\boldsymbol{f}_{s}^{n+1}\in \boldsymbol{L}^{2}(\unicode[STIX]{x1D6FA}_{s})$
, find
$\boldsymbol{f}_{s}^{n+1}\in \boldsymbol{L}^{2}(\unicode[STIX]{x1D6FA}_{s})$
, find
 $(\boldsymbol{v}^{n+1},\boldsymbol{d}^{n+1})\in \boldsymbol{Z}^{\ast }$
and
$(\boldsymbol{v}^{n+1},\boldsymbol{d}^{n+1})\in \boldsymbol{Z}^{\ast }$
and
 $p^{n+1}\in Q^{\ast }$
such that (10.20)
$p^{n+1}\in Q^{\ast }$
such that (10.20) $$\begin{eqnarray}\displaystyle & & \displaystyle a(\boldsymbol{v}^{n+1},\boldsymbol{d}^{n+1};\boldsymbol{w},\boldsymbol{\unicode[STIX]{x1D713}})^{\ast }+\biggl(E\,\boldsymbol{S}_{s}(\boldsymbol{d}^{n+1}),\frac{1}{\unicode[STIX]{x1D6E5}t}\unicode[STIX]{x1D6FB}\boldsymbol{\unicode[STIX]{x1D713}}\biggr)_{s}+b(p^{n+1};\boldsymbol{v})^{\ast }\nonumber\\ \displaystyle & & \displaystyle \quad =F_{f}^{n+1}(\boldsymbol{w})+F_{s}^{n+1}\biggl(\frac{\boldsymbol{\unicode[STIX]{x1D713}}}{\unicode[STIX]{x1D6E5}t}\biggr)-a(\boldsymbol{R}_{f}^{n+1},\mathbf{0};\boldsymbol{w},\boldsymbol{\unicode[STIX]{x1D713}})^{\ast }\quad \text{for all}~(\boldsymbol{w},\boldsymbol{\unicode[STIX]{x1D713}})\in \boldsymbol{Z}^{\ast }\nonumber\\ \displaystyle & & \displaystyle b(q;\boldsymbol{v}^{n+1})^{\ast }=0\quad \text{for all}~q\in Q^{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle a(\boldsymbol{v}^{n+1},\boldsymbol{d}^{n+1};\boldsymbol{w},\boldsymbol{\unicode[STIX]{x1D713}})^{\ast }+\biggl(E\,\boldsymbol{S}_{s}(\boldsymbol{d}^{n+1}),\frac{1}{\unicode[STIX]{x1D6E5}t}\unicode[STIX]{x1D6FB}\boldsymbol{\unicode[STIX]{x1D713}}\biggr)_{s}+b(p^{n+1};\boldsymbol{v})^{\ast }\nonumber\\ \displaystyle & & \displaystyle \quad =F_{f}^{n+1}(\boldsymbol{w})+F_{s}^{n+1}\biggl(\frac{\boldsymbol{\unicode[STIX]{x1D713}}}{\unicode[STIX]{x1D6E5}t}\biggr)-a(\boldsymbol{R}_{f}^{n+1},\mathbf{0};\boldsymbol{w},\boldsymbol{\unicode[STIX]{x1D713}})^{\ast }\quad \text{for all}~(\boldsymbol{w},\boldsymbol{\unicode[STIX]{x1D713}})\in \boldsymbol{Z}^{\ast }\nonumber\\ \displaystyle & & \displaystyle b(q;\boldsymbol{v}^{n+1})^{\ast }=0\quad \text{for all}~q\in Q^{\ast }.\end{eqnarray}$$
-
(3) Update the fluid domain to obtain
 $\unicode[STIX]{x1D6FA}_{f}^{n+1}$
.
$\unicode[STIX]{x1D6FA}_{f}^{n+1}$
.
For notation we have set
 $$\begin{eqnarray}\boldsymbol{S}_{s}(\boldsymbol{d})=\frac{1}{2(1+\unicode[STIX]{x1D708})}(\unicode[STIX]{x1D6FB}\boldsymbol{d}+(\unicode[STIX]{x1D6FB}\boldsymbol{d})^{T})+\frac{\unicode[STIX]{x1D708}}{(1+\unicode[STIX]{x1D708})(1-2\unicode[STIX]{x1D708})}(\unicode[STIX]{x1D6FB}\cdot \boldsymbol{d})\boldsymbol{I}\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{S}_{s}(\boldsymbol{d})=\frac{1}{2(1+\unicode[STIX]{x1D708})}(\unicode[STIX]{x1D6FB}\boldsymbol{d}+(\unicode[STIX]{x1D6FB}\boldsymbol{d})^{T})+\frac{\unicode[STIX]{x1D708}}{(1+\unicode[STIX]{x1D708})(1-2\unicode[STIX]{x1D708})}(\unicode[STIX]{x1D6FB}\cdot \boldsymbol{d})\boldsymbol{I}\end{eqnarray}$$
so that we can write
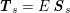 $\boldsymbol{T}_{s}=E\,\boldsymbol{S}_{s}$
. Moreover, given
$\boldsymbol{T}_{s}=E\,\boldsymbol{S}_{s}$
. Moreover, given
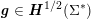 $\boldsymbol{g}\in \boldsymbol{H}^{1/2}(\unicode[STIX]{x1D6F4}^{\ast })$
, we let
$\boldsymbol{g}\in \boldsymbol{H}^{1/2}(\unicode[STIX]{x1D6F4}^{\ast })$
, we let
 $$\begin{eqnarray}\boldsymbol{R}_{f}(\boldsymbol{g})\in \boldsymbol{H}^{\mathit{div}}(\unicode[STIX]{x1D6FA}_{f}^{\ast })=\{\boldsymbol{v}\in \boldsymbol{H}^{1}(\unicode[STIX]{x1D6FA}_{f}^{\ast }):\,\unicode[STIX]{x1D6FB}\cdot \boldsymbol{v}=0\}\quad \text{and}\quad \boldsymbol{R}_{s}(\boldsymbol{g})\in \boldsymbol{H}^{1}(\unicode[STIX]{x1D6FA}_{s})\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{R}_{f}(\boldsymbol{g})\in \boldsymbol{H}^{\mathit{div}}(\unicode[STIX]{x1D6FA}_{f}^{\ast })=\{\boldsymbol{v}\in \boldsymbol{H}^{1}(\unicode[STIX]{x1D6FA}_{f}^{\ast }):\,\unicode[STIX]{x1D6FB}\cdot \boldsymbol{v}=0\}\quad \text{and}\quad \boldsymbol{R}_{s}(\boldsymbol{g})\in \boldsymbol{H}^{1}(\unicode[STIX]{x1D6FA}_{s})\end{eqnarray}$$
denote two lifting functions for the fluid–structure interface continuity, given by
 $$\begin{eqnarray}\boldsymbol{R}_{f}(\boldsymbol{g})-\boldsymbol{R}_{s}(\boldsymbol{g})=-\boldsymbol{g}/\unicode[STIX]{x1D6E5}t\quad \text{on }\unicode[STIX]{x1D6F4}^{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{R}_{f}(\boldsymbol{g})-\boldsymbol{R}_{s}(\boldsymbol{g})=-\boldsymbol{g}/\unicode[STIX]{x1D6E5}t\quad \text{on }\unicode[STIX]{x1D6F4}^{\ast }.\end{eqnarray}$$
Due to the arbitrariness of one of these functions, in what follows we set
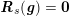 $\boldsymbol{R}_{s}(\boldsymbol{g})=\mathbf{0}$
. Moreover, when applied to function
$\boldsymbol{R}_{s}(\boldsymbol{g})=\mathbf{0}$
. Moreover, when applied to function
![]() $\boldsymbol{d}^{n-1}$
, it is possible to set
$\boldsymbol{d}^{n-1}$
, it is possible to set
 $\boldsymbol{R}_{f}^{n}=\boldsymbol{R}_{f}(\boldsymbol{d}^{n-1})$
. Finally, the functionals
$\boldsymbol{R}_{f}^{n}=\boldsymbol{R}_{f}(\boldsymbol{d}^{n-1})$
. Finally, the functionals
![]() $F_{f}^{n+1}$
and
$F_{f}^{n+1}$
and
![]() $F_{s}^{n+1}$
in (10.20) account for forcing terms, boundary data on
$F_{s}^{n+1}$
in (10.20) account for forcing terms, boundary data on
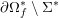 $\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}_{f}^{\ast }\setminus \unicode[STIX]{x1D6F4}^{\ast }$
and
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}_{f}^{\ast }\setminus \unicode[STIX]{x1D6F4}^{\ast }$
and
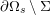 $\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}_{s}\setminus \unicode[STIX]{x1D6F4}$
and terms coming from the time discretization at previous time steps.
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}_{s}\setminus \unicode[STIX]{x1D6F4}$
and terms coming from the time discretization at previous time steps.
Regarding the parameter estimation problem, once the problem has been discretized in time, the minimization of the cost functional
 $$\begin{eqnarray}\widetilde{{\mathcal{J}}}_{k}(\boldsymbol{d},E)=\int _{\unicode[STIX]{x1D6F4}}(\boldsymbol{d}_{\mathit{meas}}(\boldsymbol{x},\unicode[STIX]{x1D70F}^{k})-\boldsymbol{d}(\boldsymbol{x},\unicode[STIX]{x1D70F}^{k}))^{2}\text{d}\unicode[STIX]{x1D70E}+\frac{\unicode[STIX]{x1D6FC}_{E}}{2}\int _{\unicode[STIX]{x1D6FA}_{s}}(E(\boldsymbol{x},\unicode[STIX]{x1D70F}^{k})-E_{\mathit{ref}})^{2}\text{d}\boldsymbol{x}\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{{\mathcal{J}}}_{k}(\boldsymbol{d},E)=\int _{\unicode[STIX]{x1D6F4}}(\boldsymbol{d}_{\mathit{meas}}(\boldsymbol{x},\unicode[STIX]{x1D70F}^{k})-\boldsymbol{d}(\boldsymbol{x},\unicode[STIX]{x1D70F}^{k}))^{2}\text{d}\unicode[STIX]{x1D70E}+\frac{\unicode[STIX]{x1D6FC}_{E}}{2}\int _{\unicode[STIX]{x1D6FA}_{s}}(E(\boldsymbol{x},\unicode[STIX]{x1D70F}^{k})-E_{\mathit{ref}})^{2}\text{d}\boldsymbol{x}\end{eqnarray}$$
for each
 $k=1,2,\ldots ,K$
is considered by Perego et al. (Reference Perego, Veneziani and Vergara2011), under the constraint (10.20). Hence, a system of KKT conditions can be derived relying on the standard Lagrange multiplier approach (see Section 9.1.2). With this aim we introduce the Lagrangian functional at time
$k=1,2,\ldots ,K$
is considered by Perego et al. (Reference Perego, Veneziani and Vergara2011), under the constraint (10.20). Hence, a system of KKT conditions can be derived relying on the standard Lagrange multiplier approach (see Section 9.1.2). With this aim we introduce the Lagrangian functional at time
![]() $\unicode[STIX]{x1D70F}^{k}$
:
$\unicode[STIX]{x1D70F}^{k}$
:
 $$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{L}}(\boldsymbol{v},p,\boldsymbol{d};\boldsymbol{\unicode[STIX]{x1D706}}_{v},\unicode[STIX]{x1D706}_{p},\boldsymbol{\unicode[STIX]{x1D706}}_{d};E)=\widetilde{{\mathcal{J}}}_{k}(\boldsymbol{d},E)+a(\boldsymbol{v},\boldsymbol{d};\boldsymbol{\unicode[STIX]{x1D706}}_{v},\boldsymbol{\unicode[STIX]{x1D706}}_{d})^{\ast }\!+\!\biggl(E\,\boldsymbol{S}_{s}(\boldsymbol{d}),\frac{1}{\unicode[STIX]{x1D6E5}t}\unicode[STIX]{x1D6FB}\boldsymbol{\unicode[STIX]{x1D706}}_{d}\biggr)_{s}\nonumber\\ \displaystyle & & \displaystyle \quad +\,b(p;\boldsymbol{\unicode[STIX]{x1D706}}_{v})^{\ast }+b(\unicode[STIX]{x1D706}_{p};\boldsymbol{v})^{\ast }-F_{f}(\boldsymbol{\unicode[STIX]{x1D706}}_{v})-F_{s}\biggl(\frac{\boldsymbol{\unicode[STIX]{x1D706}}_{d}}{\unicode[STIX]{x1D6E5}t}\biggr)+a(\boldsymbol{R}_{f},\mathbf{0};\boldsymbol{\unicode[STIX]{x1D706}}_{v},\boldsymbol{\unicode[STIX]{x1D706}}_{d})^{\ast }.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{L}}(\boldsymbol{v},p,\boldsymbol{d};\boldsymbol{\unicode[STIX]{x1D706}}_{v},\unicode[STIX]{x1D706}_{p},\boldsymbol{\unicode[STIX]{x1D706}}_{d};E)=\widetilde{{\mathcal{J}}}_{k}(\boldsymbol{d},E)+a(\boldsymbol{v},\boldsymbol{d};\boldsymbol{\unicode[STIX]{x1D706}}_{v},\boldsymbol{\unicode[STIX]{x1D706}}_{d})^{\ast }\!+\!\biggl(E\,\boldsymbol{S}_{s}(\boldsymbol{d}),\frac{1}{\unicode[STIX]{x1D6E5}t}\unicode[STIX]{x1D6FB}\boldsymbol{\unicode[STIX]{x1D706}}_{d}\biggr)_{s}\nonumber\\ \displaystyle & & \displaystyle \quad +\,b(p;\boldsymbol{\unicode[STIX]{x1D706}}_{v})^{\ast }+b(\unicode[STIX]{x1D706}_{p};\boldsymbol{v})^{\ast }-F_{f}(\boldsymbol{\unicode[STIX]{x1D706}}_{v})-F_{s}\biggl(\frac{\boldsymbol{\unicode[STIX]{x1D706}}_{d}}{\unicode[STIX]{x1D6E5}t}\biggr)+a(\boldsymbol{R}_{f},\mathbf{0};\boldsymbol{\unicode[STIX]{x1D706}}_{v},\boldsymbol{\unicode[STIX]{x1D706}}_{d})^{\ast }.\nonumber\end{eqnarray}$$
The dependence on the superscript
![]() $k$
is omitted. By the requirement that the gradient of
$k$
is omitted. By the requirement that the gradient of
![]() ${\mathcal{L}}$
vanishes, we obtain the following.
${\mathcal{L}}$
vanishes, we obtain the following.
-
∙ The adjoint problem, by forcing to zero the (Gâteaux) derivatives of the Lagrangian functional with respect to
 $(\boldsymbol{v},p,\boldsymbol{d})$
, which in fact is a time-discretized FSI problem (see below for the interface condition). Find
$(\boldsymbol{v},p,\boldsymbol{d})$
, which in fact is a time-discretized FSI problem (see below for the interface condition). Find
 $(\boldsymbol{\unicode[STIX]{x1D706}}_{v},\boldsymbol{\unicode[STIX]{x1D706}}_{d})\in \boldsymbol{Z}^{\ast }$
,
$(\boldsymbol{\unicode[STIX]{x1D706}}_{v},\boldsymbol{\unicode[STIX]{x1D706}}_{d})\in \boldsymbol{Z}^{\ast }$
,
 $\unicode[STIX]{x1D706}_{p}\in Q^{\ast }$
such that (10.21)
$\unicode[STIX]{x1D706}_{p}\in Q^{\ast }$
such that (10.21) $$\begin{eqnarray}\displaystyle & & \displaystyle a(\boldsymbol{v},\boldsymbol{\unicode[STIX]{x1D713}};\boldsymbol{\unicode[STIX]{x1D706}}_{v},\boldsymbol{\unicode[STIX]{x1D706}}_{d})^{\ast }+\biggl(E\,\boldsymbol{S}_{s}\biggl(\frac{\boldsymbol{\unicode[STIX]{x1D713}}}{\unicode[STIX]{x1D6E5}t}\biggr),\unicode[STIX]{x1D6FB}\boldsymbol{\unicode[STIX]{x1D706}}_{d}\biggr)_{s}+b(\unicode[STIX]{x1D706}_{p};\boldsymbol{w})^{\ast }\nonumber\\ \displaystyle & & \displaystyle \quad +\,\int _{\unicode[STIX]{x1D6F4}}(\boldsymbol{d}-\boldsymbol{d}_{\mathit{meas}})\cdot \boldsymbol{\unicode[STIX]{x1D713}}\text{d}\unicode[STIX]{x1D70E}=0,\nonumber\\ \displaystyle & & \displaystyle b(q;\boldsymbol{\unicode[STIX]{x1D706}}_{v})^{\ast }=0\quad \text{for all}~(\boldsymbol{w},\boldsymbol{\unicode[STIX]{x1D713}})\in \boldsymbol{Z}^{\ast },q\in Q^{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle a(\boldsymbol{v},\boldsymbol{\unicode[STIX]{x1D713}};\boldsymbol{\unicode[STIX]{x1D706}}_{v},\boldsymbol{\unicode[STIX]{x1D706}}_{d})^{\ast }+\biggl(E\,\boldsymbol{S}_{s}\biggl(\frac{\boldsymbol{\unicode[STIX]{x1D713}}}{\unicode[STIX]{x1D6E5}t}\biggr),\unicode[STIX]{x1D6FB}\boldsymbol{\unicode[STIX]{x1D706}}_{d}\biggr)_{s}+b(\unicode[STIX]{x1D706}_{p};\boldsymbol{w})^{\ast }\nonumber\\ \displaystyle & & \displaystyle \quad +\,\int _{\unicode[STIX]{x1D6F4}}(\boldsymbol{d}-\boldsymbol{d}_{\mathit{meas}})\cdot \boldsymbol{\unicode[STIX]{x1D713}}\text{d}\unicode[STIX]{x1D70E}=0,\nonumber\\ \displaystyle & & \displaystyle b(q;\boldsymbol{\unicode[STIX]{x1D706}}_{v})^{\ast }=0\quad \text{for all}~(\boldsymbol{w},\boldsymbol{\unicode[STIX]{x1D713}})\in \boldsymbol{Z}^{\ast },q\in Q^{\ast }.\end{eqnarray}$$
-
∙ The optimality condition
by forcing to zero the derivative with respect to $$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D711}\,\boldsymbol{S}_{s}(\boldsymbol{d}),\unicode[STIX]{x1D6FB}\boldsymbol{\unicode[STIX]{x1D706}}_{d})_{s}=0\quad \text{for all}~\unicode[STIX]{x1D711}\in L^{\infty }(\unicode[STIX]{x1D6FA}_{s}), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D711}\,\boldsymbol{S}_{s}(\boldsymbol{d}),\unicode[STIX]{x1D6FB}\boldsymbol{\unicode[STIX]{x1D706}}_{d})_{s}=0\quad \text{for all}~\unicode[STIX]{x1D711}\in L^{\infty }(\unicode[STIX]{x1D6FA}_{s}), & & \displaystyle \nonumber\end{eqnarray}$$
 $E$
.
$E$
.
-
∙ We also require the following state problem. Find
 $(\boldsymbol{v},\boldsymbol{d})\in \boldsymbol{Z}^{\ast }$
,
$(\boldsymbol{v},\boldsymbol{d})\in \boldsymbol{Z}^{\ast }$
,
 $p\in Q^{\ast }$
such that formally obtained by deriving the Lagrangian with respect to
$p\in Q^{\ast }$
such that formally obtained by deriving the Lagrangian with respect to $$\begin{eqnarray}\displaystyle & & \displaystyle a(\boldsymbol{v},\boldsymbol{d};\boldsymbol{w},\boldsymbol{\unicode[STIX]{x1D713}})^{\ast }+\biggl(E\,\boldsymbol{S}_{s}(\boldsymbol{d}),\frac{1}{\unicode[STIX]{x1D6E5}t}\unicode[STIX]{x1D6FB}\boldsymbol{\unicode[STIX]{x1D713}}\biggr)_{s}+b(p;\boldsymbol{w})^{\ast }\nonumber\\ \displaystyle & & \displaystyle \quad =F_{f}(\boldsymbol{w})+F_{s}\biggl(\frac{\boldsymbol{\unicode[STIX]{x1D713}}}{\unicode[STIX]{x1D6E5}t}\biggr)-a(\boldsymbol{R}_{f},\mathbf{0};\boldsymbol{w},\boldsymbol{\unicode[STIX]{x1D713}})^{\ast }\nonumber\\ \displaystyle & & \displaystyle b(q;\boldsymbol{v})^{\ast }=0\quad \text{for all}~(\boldsymbol{w},\boldsymbol{\unicode[STIX]{x1D713}})\in \boldsymbol{Z}^{\ast },q\in Q^{\ast },\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle a(\boldsymbol{v},\boldsymbol{d};\boldsymbol{w},\boldsymbol{\unicode[STIX]{x1D713}})^{\ast }+\biggl(E\,\boldsymbol{S}_{s}(\boldsymbol{d}),\frac{1}{\unicode[STIX]{x1D6E5}t}\unicode[STIX]{x1D6FB}\boldsymbol{\unicode[STIX]{x1D713}}\biggr)_{s}+b(p;\boldsymbol{w})^{\ast }\nonumber\\ \displaystyle & & \displaystyle \quad =F_{f}(\boldsymbol{w})+F_{s}\biggl(\frac{\boldsymbol{\unicode[STIX]{x1D713}}}{\unicode[STIX]{x1D6E5}t}\biggr)-a(\boldsymbol{R}_{f},\mathbf{0};\boldsymbol{w},\boldsymbol{\unicode[STIX]{x1D713}})^{\ast }\nonumber\\ \displaystyle & & \displaystyle b(q;\boldsymbol{v})^{\ast }=0\quad \text{for all}~(\boldsymbol{w},\boldsymbol{\unicode[STIX]{x1D713}})\in \boldsymbol{Z}^{\ast },q\in Q^{\ast },\nonumber\end{eqnarray}$$
 $(\boldsymbol{\unicode[STIX]{x1D706}}_{v},\!\unicode[STIX]{x1D706}_{p},\!\boldsymbol{\unicode[STIX]{x1D706}}_{d})$
.
$(\boldsymbol{\unicode[STIX]{x1D706}}_{v},\!\unicode[STIX]{x1D706}_{p},\!\boldsymbol{\unicode[STIX]{x1D706}}_{d})$
.
The adjoint problem, the optimality condition and the state problem yield the system of KKT conditions at each
![]() $\unicode[STIX]{x1D70F}^{k}$
, which couples two linearized FSI problems and a scalar equation.
$\unicode[STIX]{x1D70F}^{k}$
, which couples two linearized FSI problems and a scalar equation.
In particular, for the adjoint problem the interface velocity condition reads
 $$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D706}}_{v}=\frac{\boldsymbol{\unicode[STIX]{x1D706}}_{d}}{\unicode[STIX]{x1D6E5}t}\quad \text{on }\unicode[STIX]{x1D6F4}^{\ast },\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D706}}_{v}=\frac{\boldsymbol{\unicode[STIX]{x1D706}}_{d}}{\unicode[STIX]{x1D6E5}t}\quad \text{on }\unicode[STIX]{x1D6F4}^{\ast },\end{eqnarray}$$
whereas the interface stress condition is
 $$\begin{eqnarray}\boldsymbol{T}_{s}(\boldsymbol{\unicode[STIX]{x1D706}}_{d})\,\boldsymbol{n}-\boldsymbol{T}_{f}(\boldsymbol{\unicode[STIX]{x1D706}}_{v},\unicode[STIX]{x1D706}_{p})\,\boldsymbol{n}=-(\boldsymbol{d}-\boldsymbol{d}_{\mathit{meas}})\quad \text{on }\unicode[STIX]{x1D6F4}^{\ast },\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{T}_{s}(\boldsymbol{\unicode[STIX]{x1D706}}_{d})\,\boldsymbol{n}-\boldsymbol{T}_{f}(\boldsymbol{\unicode[STIX]{x1D706}}_{v},\unicode[STIX]{x1D706}_{p})\,\boldsymbol{n}=-(\boldsymbol{d}-\boldsymbol{d}_{\mathit{meas}})\quad \text{on }\unicode[STIX]{x1D6F4}^{\ast },\end{eqnarray}$$
taking into account the mismatch between the data and the solution, and modifying the homogeneous interface stress condition (4.19d ) accordingly.
The same strategies described in Section 9.2 (e.g. gradient-based methods) can be exploited to solve the KKT system numerically. To take into account the constraint
![]() $E>0$
in the case at hand, it is possible to transform the parameter as
$E>0$
in the case at hand, it is possible to transform the parameter as
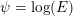 $\unicode[STIX]{x1D713}=\log (E)$
, so that
$\unicode[STIX]{x1D713}=\log (E)$
, so that
 $E=\exp (\unicode[STIX]{x1D713})>0$
for every
$E=\exp (\unicode[STIX]{x1D713})>0$
for every
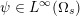 $\unicode[STIX]{x1D713}\in L^{\infty }(\unicode[STIX]{x1D6FA}_{s})$
, and then optimize with respect to
$\unicode[STIX]{x1D713}\in L^{\infty }(\unicode[STIX]{x1D6FA}_{s})$
, and then optimize with respect to
![]() $\unicode[STIX]{x1D713}$
. Finally, a finite element discretization in space is required to solve the state and the adjoint problem numerically.
$\unicode[STIX]{x1D713}$
. Finally, a finite element discretization in space is required to solve the state and the adjoint problem numerically.
By construction, this approach provides an estimate for
![]() $E$
at each time; a possible option is then to average them to obtain a unique estimate, although this may suffer from instabilities in the presence of highly noisy data. A more robust approach is to solve the minimization problem over time. In this case, however, the complexity of the problem would increase, due to the inclusion of the shape derivatives in the minimization problem. In Figure 10.2 we show the number of iterations and the convergence history for the algorithm described above for the estimation of Young’s modulus.
$E$
at each time; a possible option is then to average them to obtain a unique estimate, although this may suffer from instabilities in the presence of highly noisy data. A more robust approach is to solve the minimization problem over time. In this case, however, the complexity of the problem would increase, due to the inclusion of the shape derivatives in the minimization problem. In Figure 10.2 we show the number of iterations and the convergence history for the algorithm described above for the estimation of Young’s modulus.

Figure 10.2. Convergence history for the estimation of Young’s modulus by means of the algorithm proposed by Perego et al. (Reference Perego, Veneziani and Vergara2011). Rectangular fluid and structure domains are used, with synthetic measurements generated by means of forward FSI simulations. Numerical results were obtained using the MATLAB finite element library MLife.
10.3.2 A Kalman filter approach for estimating material parameters in cardiac mechanics
In this section we illustrate a Kalman filter approach introduced by Xi et al. (Reference Xi, Lamata, Lee, Moireau, Chapelle and Smith2011) to estimate material parameters occurring in the mechanical model describing myocardial contractility. Only passive mechanics is modelled, making a quasi-static assumption, and without taking into account the electromechanical coupling. A transversely isotropic Guccione’s constitutive law (Guccione et al. Reference Guccione, Mcculloch and Waldman1991) is used, and four parameters are estimated in silico from noisy displacement measurements of material points located on the myocardial surface. In principle, a similar approach can also be used, for example, to identify the material parameters affecting the orthotropic model (7.24).
The transversely isotropic strain energy function in the Guccione law can be expressed as
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}(\boldsymbol{E})=\frac{1}{2}\unicode[STIX]{x1D703}_{1}(\text{e}^{Q}-1),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}(\boldsymbol{E})=\frac{1}{2}\unicode[STIX]{x1D703}_{1}(\text{e}^{Q}-1),\end{eqnarray}$$
where
 $$\begin{eqnarray}Q=\unicode[STIX]{x1D703}_{2}E_{ff}^{2}+\unicode[STIX]{x1D703}_{3}(E_{ss}^{2}+E_{nn}^{2}+2E_{sn}^{2})+\unicode[STIX]{x1D703}_{4}(2E_{fs}^{2}+2E_{fn}^{2}).\end{eqnarray}$$
$$\begin{eqnarray}Q=\unicode[STIX]{x1D703}_{2}E_{ff}^{2}+\unicode[STIX]{x1D703}_{3}(E_{ss}^{2}+E_{nn}^{2}+2E_{sn}^{2})+\unicode[STIX]{x1D703}_{4}(2E_{fs}^{2}+2E_{fn}^{2}).\end{eqnarray}$$
Here
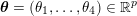 $\boldsymbol{\unicode[STIX]{x1D703}}=(\unicode[STIX]{x1D703}_{1},\ldots ,\unicode[STIX]{x1D703}_{4})\in \mathbb{R}^{p}$
denotes a vector of
$\boldsymbol{\unicode[STIX]{x1D703}}=(\unicode[STIX]{x1D703}_{1},\ldots ,\unicode[STIX]{x1D703}_{4})\in \mathbb{R}^{p}$
denotes a vector of
![]() $p=4$
material parameters, and
$p=4$
material parameters, and
![]() $E_{ij}$
is the
$E_{ij}$
is the
![]() $(i,j)$
th component of the Green–Lagrange strain tensor
$(i,j)$
th component of the Green–Lagrange strain tensor
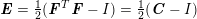 $\boldsymbol{E}={\textstyle \frac{1}{2}}(\boldsymbol{F}^{T}\boldsymbol{F}-I)={\textstyle \frac{1}{2}}(\boldsymbol{C}-I)$
, with
$\boldsymbol{E}={\textstyle \frac{1}{2}}(\boldsymbol{F}^{T}\boldsymbol{F}-I)={\textstyle \frac{1}{2}}(\boldsymbol{C}-I)$
, with
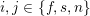 $i,j\in \{f,s,n\}$
denoting fibre, sheet and sheet-normal directions, respectively. After performing spatial discretization, at each time step the augmented state
$i,j\in \{f,s,n\}$
denoting fibre, sheet and sheet-normal directions, respectively. After performing spatial discretization, at each time step the augmented state
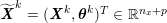 $\widetilde{\boldsymbol{X}}^{k}=(\boldsymbol{X}^{k},\boldsymbol{\unicode[STIX]{x1D703}}^{k})^{T}\in \mathbb{R}^{n_{x}+p}$
, made up of the deformed configuration
$\widetilde{\boldsymbol{X}}^{k}=(\boldsymbol{X}^{k},\boldsymbol{\unicode[STIX]{x1D703}}^{k})^{T}\in \mathbb{R}^{n_{x}+p}$
, made up of the deformed configuration
![]() $\boldsymbol{X}^{k}$
and the material parameter vector
$\boldsymbol{X}^{k}$
and the material parameter vector
![]() $\boldsymbol{\unicode[STIX]{x1D703}}^{k}$
, has to be determined by solving a non-linear problem of the form
$\boldsymbol{\unicode[STIX]{x1D703}}^{k}$
, has to be determined by solving a non-linear problem of the form
 $$\begin{eqnarray}\widetilde{\boldsymbol{X}}^{k}=\mathbf{f}(\widetilde{\boldsymbol{X}}^{k-1},\boldsymbol{u}^{k-1})+\boldsymbol{\unicode[STIX]{x1D700}}^{k},\quad \mathbf{f}(\widetilde{\boldsymbol{X}}^{k-1},\boldsymbol{u}^{k-1})=\left[\begin{array}{@{}c@{}}G(\boldsymbol{\unicode[STIX]{x1D703}}^{k-1},\boldsymbol{u}^{k-1})\\ \boldsymbol{\unicode[STIX]{x1D703}}^{k-1}\end{array}\right]\!,\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{\boldsymbol{X}}^{k}=\mathbf{f}(\widetilde{\boldsymbol{X}}^{k-1},\boldsymbol{u}^{k-1})+\boldsymbol{\unicode[STIX]{x1D700}}^{k},\quad \mathbf{f}(\widetilde{\boldsymbol{X}}^{k-1},\boldsymbol{u}^{k-1})=\left[\begin{array}{@{}c@{}}G(\boldsymbol{\unicode[STIX]{x1D703}}^{k-1},\boldsymbol{u}^{k-1})\\ \boldsymbol{\unicode[STIX]{x1D703}}^{k-1}\end{array}\right]\!,\end{eqnarray}$$
where the input vector
![]() $\boldsymbol{u}^{k-1}$
at time
$\boldsymbol{u}^{k-1}$
at time
![]() $k-1$
is given by the external forces, with observations
$k-1$
is given by the external forces, with observations
 $$\begin{eqnarray}\boldsymbol{Z}^{k}=\boldsymbol{h}(\widetilde{\boldsymbol{X}}^{k}+\boldsymbol{w}^{k}),\quad k=1,\ldots ,K.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{Z}^{k}=\boldsymbol{h}(\widetilde{\boldsymbol{X}}^{k}+\boldsymbol{w}^{k}),\quad k=1,\ldots ,K.\end{eqnarray}$$
Xi et al. (Reference Xi, Lamata, Lee, Moireau, Chapelle and Smith2011) take
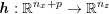 $\boldsymbol{h}:\mathbb{R}^{n_{x}+p}\rightarrow \mathbb{R}^{n_{z}}$
to be a linear (interpolation) matrix
$\boldsymbol{h}:\mathbb{R}^{n_{x}+p}\rightarrow \mathbb{R}^{n_{z}}$
to be a linear (interpolation) matrix
 $H\in \mathbb{R}^{(n_{x}+p)\times n_{z}}$
, mapping the augmented state vector to the coordinates of the points where measurements are acquired. These measurements are assumed to be contaminated by a noise term
$H\in \mathbb{R}^{(n_{x}+p)\times n_{z}}$
, mapping the augmented state vector to the coordinates of the points where measurements are acquired. These measurements are assumed to be contaminated by a noise term
![]() $\boldsymbol{w}^{k}$
with zero mean and covariance
$\boldsymbol{w}^{k}$
with zero mean and covariance
![]() $R_{k}$
; note that the material parameter has no explicit time dependence. Nevertheless, as already pointed out, the filter will provide recursively updated estimates of
$R_{k}$
; note that the material parameter has no explicit time dependence. Nevertheless, as already pointed out, the filter will provide recursively updated estimates of
![]() $\boldsymbol{\unicode[STIX]{x1D703}}^{k}$
. The goal is thus to compute the estimate
$\boldsymbol{\unicode[STIX]{x1D703}}^{k}$
. The goal is thus to compute the estimate
![]() $\boldsymbol{\unicode[STIX]{x1D703}}^{K}$
at the final time
$\boldsymbol{\unicode[STIX]{x1D703}}^{K}$
at the final time
![]() $t=t^{K}$
.
$t=t^{K}$
.
Moreover, since the augmented state vector
![]() $\widetilde{\boldsymbol{X}}^{k}$
does not depend on the deformed configuration
$\widetilde{\boldsymbol{X}}^{k}$
does not depend on the deformed configuration
![]() $\widetilde{\boldsymbol{X}}^{k-1}$
, the rank of the error covariance matrix
$\widetilde{\boldsymbol{X}}^{k-1}$
, the rank of the error covariance matrix
![]() $\widetilde{P}_{k}$
at each step will be equal to
$\widetilde{P}_{k}$
at each step will be equal to
![]() $p$
. This is a crucial point in order to devise a reduced-order UKF, making it possible to (i) store a covariance matrix of dimension
$p$
. This is a crucial point in order to devise a reduced-order UKF, making it possible to (i) store a covariance matrix of dimension
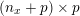 $(n_{x}+p)\times p$
, (ii) perform inversion of
$(n_{x}+p)\times p$
, (ii) perform inversion of
![]() $p\times p$
matrices and, even more importantly, (iii) decrease the number of model evaluations required by the filter at each time step from
$p\times p$
matrices and, even more importantly, (iii) decrease the number of model evaluations required by the filter at each time step from
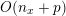 $O(n_{x}+p)$
to
$O(n_{x}+p)$
to
![]() $O(p)$
.
$O(p)$
.
Slight differences arise with respect to the UKF formulation addressed in Section 10.2.3, due to the reduction of the estimation process to the subset of
![]() $\widetilde{\boldsymbol{X}}^{k}$
corresponding to the
$\widetilde{\boldsymbol{X}}^{k}$
corresponding to the
![]() $p$
parameter components. The filtering algorithm consists of three steps.
$p$
parameter components. The filtering algorithm consists of three steps.
-
∙ Initialization. A singular value decomposition
 $P_{0}^{a}=L_{0}^{a}\unicode[STIX]{x1D6EC}_{0}^{a}(L_{0}^{a})^{T}$
of the initial error covariance
$P_{0}^{a}=L_{0}^{a}\unicode[STIX]{x1D6EC}_{0}^{a}(L_{0}^{a})^{T}$
of the initial error covariance
 $P_{0}^{a}\in \mathbb{R}^{(n_{x}+p)\times (n_{x}+p)}$
is performed. For instance,
$P_{0}^{a}\in \mathbb{R}^{(n_{x}+p)\times (n_{x}+p)}$
is performed. For instance,
 $P_{0}^{a}$
can be given by a diagonal matrix with
$P_{0}^{a}$
can be given by a diagonal matrix with
 $p$
non-zero entries representing the variances of the initial (or background) parameter estimates. Letting
$p$
non-zero entries representing the variances of the initial (or background) parameter estimates. Letting
 $L_{0,p}^{a}$
be the matrix whose columns are the first
$L_{0,p}^{a}$
be the matrix whose columns are the first
 $p$
singular vectors of
$p$
singular vectors of
 $L_{0}^{a}$
and
$L_{0}^{a}$
and
 $\unicode[STIX]{x1D6EC}_{0,p}^{a}$
, the
$\unicode[STIX]{x1D6EC}_{0,p}^{a}$
, the
 $p\times p$
diagonal matrix of the singular values, the reduced-rank square-root approximation
$p\times p$
diagonal matrix of the singular values, the reduced-rank square-root approximation
 $S_{0}^{a}\in \mathbb{R}^{(n_{x}+p)\times p}$
can be obtained as
$S_{0}^{a}\in \mathbb{R}^{(n_{x}+p)\times p}$
can be obtained as  $$\begin{eqnarray}S_{0}^{a}=L_{0,p}^{a}\sqrt{\unicode[STIX]{x1D6EC}_{0,p}^{a}}.\end{eqnarray}$$
$$\begin{eqnarray}S_{0}^{a}=L_{0,p}^{a}\sqrt{\unicode[STIX]{x1D6EC}_{0,p}^{a}}.\end{eqnarray}$$
-
∙ Prediction (or time update). At each step
 $k=1,\ldots ,$
starting from the assimilated state
$k=1,\ldots ,$
starting from the assimilated state
 $\widehat{\widetilde{\boldsymbol{X}}}_{a}^{k-1}$
at step
$\widehat{\widetilde{\boldsymbol{X}}}_{a}^{k-1}$
at step
 $k-1$
, a set of sigma points is selected as The sigma points are then transformed via the state dynamics to obtain
$k-1$
, a set of sigma points is selected as The sigma points are then transformed via the state dynamics to obtain $$\begin{eqnarray}\widetilde{x}_{a,(i)}^{k-1}=\widehat{\widetilde{\boldsymbol{X}}}_{a}^{k-1}+(S_{k-1}^{a})_{i},\quad \widetilde{x}_{a,(p+i)}^{k-1}=\widehat{\widetilde{\boldsymbol{X}}}_{a}^{k-1}-(S_{k-1}^{a})_{i},\quad i=1,\ldots ,p.\end{eqnarray}$$
and the mean
$$\begin{eqnarray}\widetilde{x}_{a,(i)}^{k-1}=\widehat{\widetilde{\boldsymbol{X}}}_{a}^{k-1}+(S_{k-1}^{a})_{i},\quad \widetilde{x}_{a,(p+i)}^{k-1}=\widehat{\widetilde{\boldsymbol{X}}}_{a}^{k-1}-(S_{k-1}^{a})_{i},\quad i=1,\ldots ,p.\end{eqnarray}$$
and the mean $$\begin{eqnarray}\widetilde{x}_{f,(i)}^{k}=\mathbf{f}(\widetilde{x}_{a,(i)}^{k-1},\boldsymbol{u}^{k-1}),\quad i=1,\ldots ,2p,\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{x}_{f,(i)}^{k}=\mathbf{f}(\widetilde{x}_{a,(i)}^{k-1},\boldsymbol{u}^{k-1}),\quad i=1,\ldots ,2p,\end{eqnarray}$$
 $\widehat{\widetilde{\boldsymbol{X}}}_{f}^{k}$
and the error covariance
$\widehat{\widetilde{\boldsymbol{X}}}_{f}^{k}$
and the error covariance
 $P_{k}^{f}$
are estimated as To preserve the low-rank structure of the correlation matrix
$P_{k}^{f}$
are estimated as To preserve the low-rank structure of the correlation matrix $$\begin{eqnarray}\widehat{\widetilde{\boldsymbol{X}}}_{f}^{k}=\mathop{\sum }_{i=1}^{2p}\widetilde{x}_{f,(i)}^{k},\quad P_{k}^{f}=\mathop{\sum }_{i=1}^{2p}(\widehat{\widetilde{\boldsymbol{X}}}_{f}^{k}-\widetilde{x}_{f,(i)}^{k})(\widehat{\widetilde{\boldsymbol{X}}}_{f}^{k}-\widetilde{x}_{f,(i)}^{k})^{T}.\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\widetilde{\boldsymbol{X}}}_{f}^{k}=\mathop{\sum }_{i=1}^{2p}\widetilde{x}_{f,(i)}^{k},\quad P_{k}^{f}=\mathop{\sum }_{i=1}^{2p}(\widehat{\widetilde{\boldsymbol{X}}}_{f}^{k}-\widetilde{x}_{f,(i)}^{k})(\widehat{\widetilde{\boldsymbol{X}}}_{f}^{k}-\widetilde{x}_{f,(i)}^{k})^{T}.\end{eqnarray}$$
 $P_{k}^{f}$
, a singular value decomposition
$P_{k}^{f}$
, a singular value decomposition
 $P_{k}^{f}=L_{k}^{f}\unicode[STIX]{x1D6EC}_{0}^{f}(L_{k}^{f})^{T}$
is performed, thus yielding
$P_{k}^{f}=L_{k}^{f}\unicode[STIX]{x1D6EC}_{0}^{f}(L_{k}^{f})^{T}$
is performed, thus yielding  $$\begin{eqnarray}P_{k}^{f}=S_{k}^{f}(S_{k}^{f})^{T},\quad S_{k}^{f}=L_{k,p}^{f}\sqrt{\unicode[STIX]{x1D6EC}_{k,p}^{f}}.\end{eqnarray}$$
$$\begin{eqnarray}P_{k}^{f}=S_{k}^{f}(S_{k}^{f})^{T},\quad S_{k}^{f}=L_{k,p}^{f}\sqrt{\unicode[STIX]{x1D6EC}_{k,p}^{f}}.\end{eqnarray}$$
-
∙ Correction (or measurement update). At each step
 $k=1,\ldots ,$
the observation
$k=1,\ldots ,$
the observation
 $\boldsymbol{Z}^{k}$
is assimilated into the forecast
$\boldsymbol{Z}^{k}$
is assimilated into the forecast
 $\widehat{\widetilde{X}}_{f}^{k}$
yielding the corrected state In this case the Kalman gain can be shown to be
$\widehat{\widetilde{X}}_{f}^{k}$
yielding the corrected state In this case the Kalman gain can be shown to be $$\begin{eqnarray}\widehat{\widetilde{\boldsymbol{X}}}_{a}^{k}=\widehat{\widetilde{\boldsymbol{X}}}_{f}^{k}+K_{k}(\boldsymbol{Z}^{k}-H\widehat{\widetilde{\boldsymbol{X}}}_{f}^{k}).\end{eqnarray}$$
along with the square-root of the error covariance, given by
$$\begin{eqnarray}\widehat{\widetilde{\boldsymbol{X}}}_{a}^{k}=\widehat{\widetilde{\boldsymbol{X}}}_{f}^{k}+K_{k}(\boldsymbol{Z}^{k}-H\widehat{\widetilde{\boldsymbol{X}}}_{f}^{k}).\end{eqnarray}$$
along with the square-root of the error covariance, given by $$\begin{eqnarray}K_{k}=S_{k}^{f}(I+(HS_{k}^{f})^{T}R_{k}^{-1}HS_{k}^{f})^{-1}(HS_{k}^{f})^{T}R_{k}^{-1}\end{eqnarray}$$
Note that here, compared to the UKF formulation of Section 10.2.3, update formulas for the Kalman gain and the error covariance are directly obtained for the square-root of the covariance matrix. For further details see Simon (Reference Simon2006) or Xi et al. (Reference Xi, Lamata, Lee, Moireau, Chapelle and Smith2011).
$$\begin{eqnarray}K_{k}=S_{k}^{f}(I+(HS_{k}^{f})^{T}R_{k}^{-1}HS_{k}^{f})^{-1}(HS_{k}^{f})^{T}R_{k}^{-1}\end{eqnarray}$$
Note that here, compared to the UKF formulation of Section 10.2.3, update formulas for the Kalman gain and the error covariance are directly obtained for the square-root of the covariance matrix. For further details see Simon (Reference Simon2006) or Xi et al. (Reference Xi, Lamata, Lee, Moireau, Chapelle and Smith2011). $$\begin{eqnarray}S_{k}^{a}=S_{k}^{f}(I+(HS_{k}^{f})^{T}R_{k}^{-1}HS_{k}^{f})^{-1/2}.\end{eqnarray}$$
$$\begin{eqnarray}S_{k}^{a}=S_{k}^{f}(I+(HS_{k}^{f})^{T}R_{k}^{-1}HS_{k}^{f})^{-1/2}.\end{eqnarray}$$
Xi et al. (Reference Xi, Lamata, Lee, Moireau, Chapelle and Smith2011) show that such a reduced-order UKF is able to estimate
![]() $p=4$
(and subsequently
$p=4$
(and subsequently
![]() $p=12$
) material parameters, starting from a set of synthetic measurements generated by adding Gaussian noise to a set of noise-free measurements, obtained via model simulation for a chosen ground truth parameter vector. Myocardial dilatation is considered by loading the structure with a given ventricular pressure on the endocardium, and
$p=12$
) material parameters, starting from a set of synthetic measurements generated by adding Gaussian noise to a set of noise-free measurements, obtained via model simulation for a chosen ground truth parameter vector. Myocardial dilatation is considered by loading the structure with a given ventricular pressure on the endocardium, and
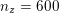 $n_{z}=600$
material points located on the epicardium and endocardium.
$n_{z}=600$
material points located on the epicardium and endocardium.
We have chosen to report this example to illustrate how to take advantage of a Kalman filter strategy in a relatively simple cardiovascular application; further details and more involved cases can be found in Moireau and Chapelle (Reference Moireau and Chapelle2011), Bertoglio et al. (Reference Bertoglio, Moireau and Gerbeau2012), Chabiniok et al. (Reference Chabiniok, Moireau, Lesault, Rahmouni, Deux and Chapelle2012), Moireau et al. (Reference Moireau, Bertoglio, Xiao, Figueroa, Taylor, Chapelle and Gerbeau2013) and Corrado et al. (Reference Corrado, Gerbeau and Moireau2015), for example. Numerical results related to parameter identification in electrophysiology by means of an ensemble Kalman filter – a technique that indeed shares several similarities with the UKF – will be shown in Section 11.2.2.
11 Including uncertainty
Moving towards model personalization – that is, the adaptation of model inputs to subject-specific conditions – the question immediately arises as to the sensitivity of model predictions to errors and uncertainties in the model inputs. The inputs to be personalized may include the computational domain (e.g. vascular networks), physical parameters (e.g. vascular material properties) and boundary conditions. Because of noise in input measurements, as well as their large biological variability, model inputs are inevitably hampered by uncertainty. Furthermore, as already seen in Section 10, not all model inputs are directly measurable, as in the case of the local mechanical properties of the arterial wall, thus calling into play the need to solve parameter estimation problems. The uncertainties carried by patient-specific features should then be incorporated into the computational model, to quantify their impact on the computed results and to obtain more reliable predictions or best/worst-case scenarios (Eck et al. Reference Eck, Donders, Sturdy, Feinberg, Delhaas, Hellevik and Huberts2016). These are the main reasons behind the very rapid growth of applications of sensitivity analysis and uncertainty quantification (UQ) to cardiovascular problems in the past decade. Since UQ is a very active field (and less mature than PDE-constrained optimization or parameter estimation) from both a mathematical and computational viewpoint, in this section we only touch on some basic, yet relevant, issues related to UQ techniques; see e.g. Sullivan (Reference Sullivan2015), Kaipio and Somersalo (Reference Kaipio and Somersalo2005) and Le Maître and Knio (Reference Le Maître and Knio2010) for a more in-depth overview of numerical aspects of UQ.
Typically, UQ problems involve a mathematical model for a process of interest, subject to some uncertainty about the correct form of this model or, more frequently, about some of its parameters. Although exhibiting substantial overlap with the field of parameter estimation and data assimilation, UQ problems also involve the propagation of uncertainty on outputs of interest, reliability or certification problems, prediction problems and, very often, consist of several of these aspects coupled together. For instance, after estimating some model parameters, we may use them to forward-propagate other uncertainties. Often, though not always, uncertainties are treated probabilistically, thus calling into play probabilistic and statistical methods. Here we focus on basic aspects related to forward propagation and backward propagation of uncertainty, for the latter case focusing on statistical inversion methods within a Bayesian framework.
11.1 Forward uncertainty quantification
The goal of forward UQ is to derive information about the uncertainties in system outputs of interest, given information about the uncertainties in the system inputs. The goal is to obtain the probability density function (PDF) of some output of interest
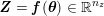 $\boldsymbol{Z}=\boldsymbol{f}(\boldsymbol{\unicode[STIX]{x1D703}})\in \mathbb{R}^{n_{z}}$
given the probability distribution of the input
$\boldsymbol{Z}=\boldsymbol{f}(\boldsymbol{\unicode[STIX]{x1D703}})\in \mathbb{R}^{n_{z}}$
given the probability distribution of the input
![]() $\boldsymbol{\unicode[STIX]{x1D703}}\in \mathbb{R}^{p}$
, or evaluate moments (e.g. the expected value and the variance), correlation functions, confidence regions or quantiles.Footnote
5
Here
$\boldsymbol{\unicode[STIX]{x1D703}}\in \mathbb{R}^{p}$
, or evaluate moments (e.g. the expected value and the variance), correlation functions, confidence regions or quantiles.Footnote
5
Here
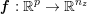 $\boldsymbol{f}:\mathbb{R}^{p}\rightarrow \mathbb{R}^{n_{z}}$
denotes an input/output map. For instance, Sankaran and Marsden (Reference Sankaran and Marsden2011) take the radius of an abdominal aortic aneurysm, the radii and the inflow velocity of the carotid artery bifurcation, and the flow split of the left and right pulmonary arteries as random variables to account for the uncertainty impact on blood flows modelled by three-dimensional Navier–Stokes equations with rigid arterial walls, by considering as outputs blood velocity and wall shear stresses.
$\boldsymbol{f}:\mathbb{R}^{p}\rightarrow \mathbb{R}^{n_{z}}$
denotes an input/output map. For instance, Sankaran and Marsden (Reference Sankaran and Marsden2011) take the radius of an abdominal aortic aneurysm, the radii and the inflow velocity of the carotid artery bifurcation, and the flow split of the left and right pulmonary arteries as random variables to account for the uncertainty impact on blood flows modelled by three-dimensional Navier–Stokes equations with rigid arterial walls, by considering as outputs blood velocity and wall shear stresses.
Once a probabilistic description of the random inputs has been provided, a suitable strategy is needed to propagate uncertainties through the model. The simplest case is one where the PDE system depends on a set of random inputs that are constant with respect to space and time. In this case, they can be described by means of a finite-dimensional random vector, with a given probability distribution. A more involved case is one where input data may vary randomly from one point of the physical domain to another (and possibly from one time instant to another); in this case, they are described in terms of random fields. Two popular strategies to describe correlated random fields include Karhunen–Loève expansions, and expansions in terms of global orthogonal polynomials (Ghanem and Spanos Reference Ghanem and Spanos2003, Xiu and Karniadakis Reference Xiu and Karniadakis2002b ). Made up of infinitely many terms, these expansions are usually truncated to approximate random fields: the milder the variations in space and time of the random field realizations, the fewer the terms retained in the expansion.
Several approaches are available for solving PDE problems with random input data. Monte Carlo (MC) methods are the most popular. These are based on independent realizations
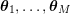 $\boldsymbol{\unicode[STIX]{x1D703}}_{1},\ldots ,\boldsymbol{\unicode[STIX]{x1D703}}_{M}$
of the random variable
$\boldsymbol{\unicode[STIX]{x1D703}}_{1},\ldots ,\boldsymbol{\unicode[STIX]{x1D703}}_{M}$
of the random variable
![]() $\boldsymbol{\unicode[STIX]{x1D703}}$
(whose probability distribution is denoted by
$\boldsymbol{\unicode[STIX]{x1D703}}$
(whose probability distribution is denoted by
![]() $\unicode[STIX]{x1D707}$
) yielding approximations of the expectation by averaging over the corresponding realizations of that quantity, that is,
$\unicode[STIX]{x1D707}$
) yielding approximations of the expectation by averaging over the corresponding realizations of that quantity, that is,
 $$\begin{eqnarray}\mathbb{E}[\boldsymbol{f}(\boldsymbol{\unicode[STIX]{x1D703}})]=\int _{\mathbb{R}^{p}}f(\boldsymbol{\unicode[STIX]{x1D703}})\unicode[STIX]{x1D707}(\text{d}\boldsymbol{\unicode[STIX]{x1D703}})\approx \frac{1}{M}\mathop{\sum }_{i=1}^{M}\boldsymbol{f}(\boldsymbol{\unicode[STIX]{x1D703}}_{i}),\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{E}[\boldsymbol{f}(\boldsymbol{\unicode[STIX]{x1D703}})]=\int _{\mathbb{R}^{p}}f(\boldsymbol{\unicode[STIX]{x1D703}})\unicode[STIX]{x1D707}(\text{d}\boldsymbol{\unicode[STIX]{x1D703}})\approx \frac{1}{M}\mathop{\sum }_{i=1}^{M}\boldsymbol{f}(\boldsymbol{\unicode[STIX]{x1D703}}_{i}),\end{eqnarray}$$
where the sample
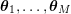 $\boldsymbol{\unicode[STIX]{x1D703}}_{1},\ldots ,\boldsymbol{\unicode[STIX]{x1D703}}_{M}$
is generated randomly from the probability distribution of
$\boldsymbol{\unicode[STIX]{x1D703}}_{1},\ldots ,\boldsymbol{\unicode[STIX]{x1D703}}_{M}$
is generated randomly from the probability distribution of
![]() $\boldsymbol{\unicode[STIX]{x1D703}}$
. Such a method requires a deterministic PDE query for each realization and a very large number of queries to achieve a small error, this latter being proportional to
$\boldsymbol{\unicode[STIX]{x1D703}}$
. Such a method requires a deterministic PDE query for each realization and a very large number of queries to achieve a small error, this latter being proportional to
![]() $1/\sqrt{M}$
. This entails an excessive computational burden, especially for systems which are already computationally expensive in their deterministic setting. See, for example, Fishman (Reference Fishman1996), Robert and Casella (Reference Robert and Casella2004) and Voss (Reference Voss2013) for more on Monte Carlo methods, and Dick, Kuo and Sloan (Reference Dick, Kuo and Sloan2013) and Giles (Reference Giles2015) for quasi-Monte Carlo and multilevel Monte Carlo methods, respectively.
$1/\sqrt{M}$
. This entails an excessive computational burden, especially for systems which are already computationally expensive in their deterministic setting. See, for example, Fishman (Reference Fishman1996), Robert and Casella (Reference Robert and Casella2004) and Voss (Reference Voss2013) for more on Monte Carlo methods, and Dick, Kuo and Sloan (Reference Dick, Kuo and Sloan2013) and Giles (Reference Giles2015) for quasi-Monte Carlo and multilevel Monte Carlo methods, respectively.
When the solution depends analytically on the random input parameters, other approaches exhibit much faster convergence rates. These include spectral (global) stochastic Galerkin (SG) methods (Ghanem and Spanos Reference Ghanem and Spanos2003, Xiu and Karniadakis Reference Xiu and Karniadakis2002a , Babuška, Tempone and Zouraris Reference Babuška, Tempone and Zouraris2004) and stochastic collocation (SC) methods (Babuška, Nobile and Tempone Reference Babuška, Nobile and Tempone2007, Xiu and Hesthaven Reference Xiu and Hesthaven2005, Nobile, Tempone and Webster Reference Nobile, Tempone and Webster2008); for a mathematical and numerical discussion, see the detailed review by Gunzburger, Webster and Zhang (Reference Gunzburger, Webster and Zhang2014) and the recent books by Le Maître and Knio (Reference Le Maître and Knio2010) and Sullivan (Reference Sullivan2015). These methods are based on the discretization of a PDE system, not only with respect to spatial variables but also with respect to the random inputs. Stochastic Galerkin methods are intrusive approaches since the physical and the probabilistic variables are coupled; stochastic sampling (SS) and interpolatory-type stochastic collocation methods are instead non-intrusive. Further, stochastic Galerkin methods require the solution of discrete systems that couple all spatial and probabilistic variables, whereas stochastic collocation methods can combine standard approximations in physical space with globally defined polynomial approximation in the probability domain, either by full polynomial spaces, tensor product polynomial spaces or sparse tensor product polynomials. The stochastic space can then be queried at any point in order to construct the PDF of the output, the interpolation in the stochastic space being built on top, and independently, of the PDE solver.
By way of illustration, Figure 11.1 gives the activation times obtained using the monodomain model coupled with the Aliev–Panfilov cell model. This computation is carried out on a patient-specific left ventricle geometry, obtained by considering different levels of tissue damage (or ischaemia), caused by an insufficient blood perfusion of the myocardium. In this case, each component of the conductivity
![]() $\boldsymbol{\unicode[STIX]{x1D6F4}}$
is multiplied by a spatial field
$\boldsymbol{\unicode[STIX]{x1D6F4}}$
is multiplied by a spatial field
![]() $\unicode[STIX]{x1D70E}(\boldsymbol{x};\boldsymbol{\unicode[STIX]{x1D703}})$
ranging from
$\unicode[STIX]{x1D70E}(\boldsymbol{x};\boldsymbol{\unicode[STIX]{x1D703}})$
ranging from
![]() $0$
(lack of conductivity, damaged tissue) to
$0$
(lack of conductivity, damaged tissue) to
![]() $1$
(regular conductivity, healthy tissue), which we refer to as relative conductivity; as soon as the position and size of the ischaemia are unknown,
$1$
(regular conductivity, healthy tissue), which we refer to as relative conductivity; as soon as the position and size of the ischaemia are unknown,
![]() $\unicode[STIX]{x1D70E}$
is a random field, depending on (a finite number
$\unicode[STIX]{x1D70E}$
is a random field, depending on (a finite number
![]() $p$
of) random inputs
$p$
of) random inputs
 $\unicode[STIX]{x1D703}_{1},\ldots ,\unicode[STIX]{x1D703}_{p}$
. We emphasize that in this case input uncertainty yields significant variability in the output, thus making uncertainty propagation a problem of interest in this context.
$\unicode[STIX]{x1D703}_{1},\ldots ,\unicode[STIX]{x1D703}_{p}$
. We emphasize that in this case input uncertainty yields significant variability in the output, thus making uncertainty propagation a problem of interest in this context.

Figure 11.1. Different degrees of tissue damage in terms of relative conductivity (a) and activation times in milliseconds (b) for a healthy case (left) and different ischaemic regions on the myocardium. The patient-specific geometry of the left ventricle has been reconstructed using the semi-automatic segmentation method proposed by Fedele et al. (Reference Fedele, Faggiano, Barbarotta, Cremonesi, Formaggia and Perotto2015). Numerical results were obtained using the finite element library redbKIT v2.1 (github.com/redbKIT/redbKIT/releases).
11.2 Inverse uncertainty quantification
Inverse UQ (or backward uncertainty propagation) problems refer to those situations in which input quantities are inferred starting from observed system outputs. Variational or sequential methods described in Sections 10.1 and 10.2 provide point estimates of the quantities of interest, given a set of observations. The statistical inversion approach provides a well-established framework to better characterize the uncertainty in the data and the resulting uncertainty in the computed estimates, adopting a Bayesian formulation. In this setting, all the model inputs included in the model are described by random variables, where randomness accounts for the available degree of information concerning their realizations, and is expressed in terms of probability distributions; as a result, the solution of the inverse UQ problem is the posterior PDF of the unknown inputs. Compared to the variational methods of Section 10.1, where classical regularization methods yield point estimates by curing the ill-posedness of the problem, statistical inversion aims at removing ill-posedness by recasting the inverse problem in a larger space of probability distributions (Kaipio and Somersalo Reference Kaipio and Somersalo2005). This strategy also enables better characterization of the prior information contained in the regularization terms in (10.2), in the form of a prior PDF of the unknown inputs. The task of Bayesian inversion is to improve the knowledge of the unknown system features starting from the prior belief and exploiting information from a set of model realizations. For more on this topic, see Stuart (Reference Stuart2010) and Sullivan (Reference Sullivan2015), for example.
11.2.1 Static problems
Assume that we are measuring an output
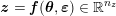 $\boldsymbol{z}=\boldsymbol{f}(\boldsymbol{\unicode[STIX]{x1D703}},\boldsymbol{\unicode[STIX]{x1D700}})\in \mathbb{R}^{n_{z}}$
in order to get information on the unknown input
$\boldsymbol{z}=\boldsymbol{f}(\boldsymbol{\unicode[STIX]{x1D703}},\boldsymbol{\unicode[STIX]{x1D700}})\in \mathbb{R}^{n_{z}}$
in order to get information on the unknown input
![]() $\boldsymbol{\unicode[STIX]{x1D703}}\in \mathbb{R}^{p}$
, and that the measured quantity is contaminated by noise
$\boldsymbol{\unicode[STIX]{x1D703}}\in \mathbb{R}^{p}$
, and that the measured quantity is contaminated by noise
![]() $\boldsymbol{\unicode[STIX]{x1D700}}$
. By treating input and output as random quantities, let us denote by
$\boldsymbol{\unicode[STIX]{x1D700}}$
. By treating input and output as random quantities, let us denote by
 $\boldsymbol{Z}\in \mathbb{R}^{n_{z}}$
and
$\boldsymbol{Z}\in \mathbb{R}^{n_{z}}$
and
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}\in \mathbb{R}^{p}$
two random variables, of which
$\boldsymbol{\unicode[STIX]{x1D6E9}}\in \mathbb{R}^{p}$
two random variables, of which
![]() $\boldsymbol{z}$
and
$\boldsymbol{z}$
and
![]() $\boldsymbol{\unicode[STIX]{x1D703}}$
denote the corresponding realizations. Very often, the noise is modelled as additive and mutually independent of
$\boldsymbol{\unicode[STIX]{x1D703}}$
denote the corresponding realizations. Very often, the noise is modelled as additive and mutually independent of
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
, so that the input/output map takes the form
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
, so that the input/output map takes the form
 $$\begin{eqnarray}\boldsymbol{Z}=\boldsymbol{f}(\boldsymbol{\unicode[STIX]{x1D6E9}})+\boldsymbol{\unicode[STIX]{x1D700}},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{Z}=\boldsymbol{f}(\boldsymbol{\unicode[STIX]{x1D6E9}})+\boldsymbol{\unicode[STIX]{x1D700}},\end{eqnarray}$$
where
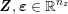 $\boldsymbol{Z},\boldsymbol{\unicode[STIX]{x1D700}}\in \mathbb{R}^{n_{z}}$
,
$\boldsymbol{Z},\boldsymbol{\unicode[STIX]{x1D700}}\in \mathbb{R}^{n_{z}}$
,
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}\in \mathbb{R}^{p}$
are random variables. Here
$\boldsymbol{\unicode[STIX]{x1D6E9}}\in \mathbb{R}^{p}$
are random variables. Here
![]() $\boldsymbol{Z}$
is called the measurement, and its realization
$\boldsymbol{Z}$
is called the measurement, and its realization
![]() $\boldsymbol{Z}=\boldsymbol{z}$
in the actual measurement process is called the data. Moreover, let
$\boldsymbol{Z}=\boldsymbol{z}$
in the actual measurement process is called the data. Moreover, let
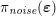 $\unicode[STIX]{x1D70B}_{\mathit{noise}}(\boldsymbol{\unicode[STIX]{x1D700}})$
denote the PDF of the noise
$\unicode[STIX]{x1D70B}_{\mathit{noise}}(\boldsymbol{\unicode[STIX]{x1D700}})$
denote the PDF of the noise
![]() $\boldsymbol{\unicode[STIX]{x1D700}}$
, usually encoding experimental errors. Before performing output measurements, all the information (e.g. structure or regularity) about the distribution of the input
$\boldsymbol{\unicode[STIX]{x1D700}}$
, usually encoding experimental errors. Before performing output measurements, all the information (e.g. structure or regularity) about the distribution of the input
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
are encapsulated in the prior PDF
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
are encapsulated in the prior PDF
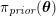 $\unicode[STIX]{x1D70B}_{\mathit{prior}}(\boldsymbol{\unicode[STIX]{x1D703}})$
, to be selected according to problem-specific considerations.
$\unicode[STIX]{x1D70B}_{\mathit{prior}}(\boldsymbol{\unicode[STIX]{x1D703}})$
, to be selected according to problem-specific considerations.
The conditional probability
 $\unicode[STIX]{x1D70B}(\boldsymbol{z}\mid \boldsymbol{\unicode[STIX]{x1D703}})$
of
$\unicode[STIX]{x1D70B}(\boldsymbol{z}\mid \boldsymbol{\unicode[STIX]{x1D703}})$
of
 $\boldsymbol{Z}\mid \boldsymbol{\unicode[STIX]{x1D6E9}}=\boldsymbol{\unicode[STIX]{x1D703}}$
(i.e. of
$\boldsymbol{Z}\mid \boldsymbol{\unicode[STIX]{x1D6E9}}=\boldsymbol{\unicode[STIX]{x1D703}}$
(i.e. of
![]() $\boldsymbol{Z}$
conditioned on
$\boldsymbol{Z}$
conditioned on
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}=\boldsymbol{\unicode[STIX]{x1D703}}$
) is the so-called (conditional) likelihood function, and expresses the likelihood of different measurement outcomes
$\boldsymbol{\unicode[STIX]{x1D6E9}}=\boldsymbol{\unicode[STIX]{x1D703}}$
) is the so-called (conditional) likelihood function, and expresses the likelihood of different measurement outcomes
![]() $\boldsymbol{z}$
given
$\boldsymbol{z}$
given
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}=\boldsymbol{\unicode[STIX]{x1D703}}$
. In our case the input/output map
$\boldsymbol{\unicode[STIX]{x1D6E9}}=\boldsymbol{\unicode[STIX]{x1D703}}$
. In our case the input/output map
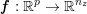 $\boldsymbol{f}:\mathbb{R}^{p}\rightarrow \mathbb{R}^{n_{z}}$
is the solution of a PDE problem, and the evaluation of the output
$\boldsymbol{f}:\mathbb{R}^{p}\rightarrow \mathbb{R}^{n_{z}}$
is the solution of a PDE problem, and the evaluation of the output
![]() $\boldsymbol{f}(\boldsymbol{\unicode[STIX]{x1D703}})$
. Thanks to the assumption of mutual independence of
$\boldsymbol{f}(\boldsymbol{\unicode[STIX]{x1D703}})$
. Thanks to the assumption of mutual independence of
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
and
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
and
![]() $\boldsymbol{\unicode[STIX]{x1D700}}$
,
$\boldsymbol{\unicode[STIX]{x1D700}}$
,
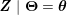 $\boldsymbol{Z}\mid \boldsymbol{\unicode[STIX]{x1D6E9}}=\boldsymbol{\unicode[STIX]{x1D703}}$
is distributed like
$\boldsymbol{Z}\mid \boldsymbol{\unicode[STIX]{x1D6E9}}=\boldsymbol{\unicode[STIX]{x1D703}}$
is distributed like
![]() $\boldsymbol{\unicode[STIX]{x1D700}}$
, that is, the likelihood function is
$\boldsymbol{\unicode[STIX]{x1D700}}$
, that is, the likelihood function is
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}(\boldsymbol{z}\mid \boldsymbol{\unicode[STIX]{x1D703}})=\unicode[STIX]{x1D70B}_{\mathit{noise}}(\boldsymbol{z}-\boldsymbol{f}(\boldsymbol{\unicode[STIX]{x1D703}})).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}(\boldsymbol{z}\mid \boldsymbol{\unicode[STIX]{x1D703}})=\unicode[STIX]{x1D70B}_{\mathit{noise}}(\boldsymbol{z}-\boldsymbol{f}(\boldsymbol{\unicode[STIX]{x1D703}})).\end{eqnarray}$$
Assuming that the measurement data
![]() $\boldsymbol{Z}=\boldsymbol{z}$
is given, in the Bayesian framework the inverse problem is to find the conditional PDF
$\boldsymbol{Z}=\boldsymbol{z}$
is given, in the Bayesian framework the inverse problem is to find the conditional PDF
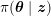 $\unicode[STIX]{x1D70B}(\boldsymbol{\unicode[STIX]{x1D703}}\mid \boldsymbol{z})$
of
$\unicode[STIX]{x1D70B}(\boldsymbol{\unicode[STIX]{x1D703}}\mid \boldsymbol{z})$
of
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
. This latter is the posterior PDF of
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
. This latter is the posterior PDF of
![]() $\boldsymbol{\unicode[STIX]{x1D6E9}}$
given the data
$\boldsymbol{\unicode[STIX]{x1D6E9}}$
given the data
![]() $\boldsymbol{Z}=\boldsymbol{z}$
and can be expressed via Bayes’ theorem as
$\boldsymbol{Z}=\boldsymbol{z}$
and can be expressed via Bayes’ theorem as
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}(\boldsymbol{\unicode[STIX]{x1D703}}\mid \boldsymbol{z})=\frac{\unicode[STIX]{x1D70B}_{\mathit{prior}}(\boldsymbol{\unicode[STIX]{x1D703}})\unicode[STIX]{x1D70B}(\boldsymbol{z}\mid \boldsymbol{\unicode[STIX]{x1D703}})}{\unicode[STIX]{x1D70B}(\boldsymbol{z})},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}(\boldsymbol{\unicode[STIX]{x1D703}}\mid \boldsymbol{z})=\frac{\unicode[STIX]{x1D70B}_{\mathit{prior}}(\boldsymbol{\unicode[STIX]{x1D703}})\unicode[STIX]{x1D70B}(\boldsymbol{z}\mid \boldsymbol{\unicode[STIX]{x1D703}})}{\unicode[STIX]{x1D70B}(\boldsymbol{z})},\end{eqnarray}$$
where
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}(\boldsymbol{z})=\int _{\mathbb{R}^{n_{z}}}\unicode[STIX]{x1D70B}(\boldsymbol{z}\mid \boldsymbol{\unicode[STIX]{x1D703}})\unicode[STIX]{x1D70B}_{\mathit{prior}}(\boldsymbol{\unicode[STIX]{x1D703}})\text{d}\boldsymbol{\unicode[STIX]{x1D703}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}(\boldsymbol{z})=\int _{\mathbb{R}^{n_{z}}}\unicode[STIX]{x1D70B}(\boldsymbol{z}\mid \boldsymbol{\unicode[STIX]{x1D703}})\unicode[STIX]{x1D70B}_{\mathit{prior}}(\boldsymbol{\unicode[STIX]{x1D703}})\text{d}\boldsymbol{\unicode[STIX]{x1D703}}\end{eqnarray}$$
plays the role of a normalization constant, and often has little importance from a computational standpoint.
Solving an inverse UQ problem in the static case – alternatively, in the literature such a problem is referred to as the stationary inverse problem – thus consists in finding a prior PDF
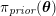 $\unicode[STIX]{x1D70B}_{\mathit{prior}}(\boldsymbol{\unicode[STIX]{x1D703}})$
, expressing the likelihood function
$\unicode[STIX]{x1D70B}_{\mathit{prior}}(\boldsymbol{\unicode[STIX]{x1D703}})$
, expressing the likelihood function
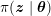 $\unicode[STIX]{x1D70B}(\boldsymbol{z}\mid \boldsymbol{\unicode[STIX]{x1D703}})$
using the interplay between the observation and the unknown, and finally developing suitable numerical techniques to explore the posterior PDF. Each of these tasks is a challenging problem from a computational standpoint; here we provide some hints on how to use this framework for a wide range of applications related to backward uncertainty quantification in cardiovascular modelling.
$\unicode[STIX]{x1D70B}(\boldsymbol{z}\mid \boldsymbol{\unicode[STIX]{x1D703}})$
using the interplay between the observation and the unknown, and finally developing suitable numerical techniques to explore the posterior PDF. Each of these tasks is a challenging problem from a computational standpoint; here we provide some hints on how to use this framework for a wide range of applications related to backward uncertainty quantification in cardiovascular modelling.
In the case where the unknown is a random variable with few components, the posterior PDF can also be visualized in the form of a non-negative function of these variables. Most applications, however, yield larger-scale inverse UQ problems, and resulting PDFs in high-dimensional spaces, for which it is much more effective to evaluate suitable point estimators, such as the maximum a posteriori estimator
 $$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D703}}_{\mathit{MAP}}=\arg \max _{\boldsymbol{\unicode[STIX]{x1D703}}\in \mathbb{R}^{p}}\unicode[STIX]{x1D70B}(\boldsymbol{\unicode[STIX]{x1D703}}\mid \boldsymbol{z})\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D703}}_{\mathit{MAP}}=\arg \max _{\boldsymbol{\unicode[STIX]{x1D703}}\in \mathbb{R}^{p}}\unicode[STIX]{x1D70B}(\boldsymbol{\unicode[STIX]{x1D703}}\mid \boldsymbol{z})\end{eqnarray}$$
or the conditional mean
 $$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D703}}_{\mathit{CM}}=\mathbb{E}[\boldsymbol{\unicode[STIX]{x1D703}}\mid \boldsymbol{z}]=\int _{\mathbb{R}^{p}}\boldsymbol{\unicode[STIX]{x1D703}}~\unicode[STIX]{x1D70B}(\boldsymbol{\unicode[STIX]{x1D703}}\mid \boldsymbol{z})\text{d}\unicode[STIX]{x1D703}.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D703}}_{\mathit{CM}}=\mathbb{E}[\boldsymbol{\unicode[STIX]{x1D703}}\mid \boldsymbol{z}]=\int _{\mathbb{R}^{p}}\boldsymbol{\unicode[STIX]{x1D703}}~\unicode[STIX]{x1D70B}(\boldsymbol{\unicode[STIX]{x1D703}}\mid \boldsymbol{z})\text{d}\unicode[STIX]{x1D703}.\end{eqnarray}$$
Evaluating the former requires the solution of an optimization problem, for example using iterative, gradient-based methods; computing the latter involves a numerical quadrature problem in high-dimensional spaces. The evaluation of variability estimators such as the conditional covariance
 $$\begin{eqnarray}\text{Cov}\,(\boldsymbol{\unicode[STIX]{x1D703}}\mid \boldsymbol{z})=\int _{\mathbb{R}^{p}}(\boldsymbol{\unicode[STIX]{x1D703}}-\boldsymbol{\unicode[STIX]{x1D703}}_{\mathit{CM}})(\boldsymbol{\unicode[STIX]{x1D703}}-\boldsymbol{\unicode[STIX]{x1D703}}_{\mathit{CM}})^{T}~\unicode[STIX]{x1D70B}(\boldsymbol{\unicode[STIX]{x1D703}}\mid \boldsymbol{z})\text{d}\unicode[STIX]{x1D703}\in \mathbb{R}^{p\times p},\end{eqnarray}$$
$$\begin{eqnarray}\text{Cov}\,(\boldsymbol{\unicode[STIX]{x1D703}}\mid \boldsymbol{z})=\int _{\mathbb{R}^{p}}(\boldsymbol{\unicode[STIX]{x1D703}}-\boldsymbol{\unicode[STIX]{x1D703}}_{\mathit{CM}})(\boldsymbol{\unicode[STIX]{x1D703}}-\boldsymbol{\unicode[STIX]{x1D703}}_{\mathit{CM}})^{T}~\unicode[STIX]{x1D70B}(\boldsymbol{\unicode[STIX]{x1D703}}\mid \boldsymbol{z})\text{d}\unicode[STIX]{x1D703}\in \mathbb{R}^{p\times p},\end{eqnarray}$$
or confidence regions, also provides further indicators for uncertainty quantification.
The simplest probabilistic model that can be used to describe experimental uncertainties is the Gaussian model, for which the noise
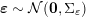 $\boldsymbol{\unicode[STIX]{x1D700}}\sim {\mathcal{N}}(\mathbf{0},\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D700}})$
is normally distributed, with mean
$\boldsymbol{\unicode[STIX]{x1D700}}\sim {\mathcal{N}}(\mathbf{0},\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D700}})$
is normally distributed, with mean
![]() $\mathbf{0}$
and covariance matrix
$\mathbf{0}$
and covariance matrix
![]() $\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D700}}$
. In this case, the likelihood function is
$\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D700}}$
. In this case, the likelihood function is
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}(\boldsymbol{z}\mid \boldsymbol{\unicode[STIX]{x1D703}})\propto \exp \biggl(-\frac{1}{2}\Vert \boldsymbol{z}-\boldsymbol{f}(\boldsymbol{\unicode[STIX]{x1D703}})\Vert _{\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D700}}^{-1}}^{2}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}(\boldsymbol{z}\mid \boldsymbol{\unicode[STIX]{x1D703}})\propto \exp \biggl(-\frac{1}{2}\Vert \boldsymbol{z}-\boldsymbol{f}(\boldsymbol{\unicode[STIX]{x1D703}})\Vert _{\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D700}}^{-1}}^{2}\biggr).\end{eqnarray}$$
If we can also assume a Gaussian model on the prior knowledge of the parameter distributions, that is,
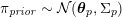 $\unicode[STIX]{x1D70B}_{\mathit{prior}}\sim {\mathcal{N}}(\boldsymbol{\unicode[STIX]{x1D703}}_{p},\unicode[STIX]{x1D6F4}_{p})$
, then the posterior PDF will be normally distributed as well, that is,
$\unicode[STIX]{x1D70B}_{\mathit{prior}}\sim {\mathcal{N}}(\boldsymbol{\unicode[STIX]{x1D703}}_{p},\unicode[STIX]{x1D6F4}_{p})$
, then the posterior PDF will be normally distributed as well, that is,
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}(\boldsymbol{\unicode[STIX]{x1D703}}\mid \boldsymbol{z})\propto \exp \biggl(-\frac{1}{2}\Vert \boldsymbol{z}-\boldsymbol{f}(\boldsymbol{\unicode[STIX]{x1D703}})\Vert _{\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D700}}^{-1}}^{2}-\frac{1}{2}\Vert \boldsymbol{\unicode[STIX]{x1D703}}-\boldsymbol{\unicode[STIX]{x1D703}}_{p}\Vert _{\unicode[STIX]{x1D6F4}_{p}^{-1}}^{2}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}(\boldsymbol{\unicode[STIX]{x1D703}}\mid \boldsymbol{z})\propto \exp \biggl(-\frac{1}{2}\Vert \boldsymbol{z}-\boldsymbol{f}(\boldsymbol{\unicode[STIX]{x1D703}})\Vert _{\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D700}}^{-1}}^{2}-\frac{1}{2}\Vert \boldsymbol{\unicode[STIX]{x1D703}}-\boldsymbol{\unicode[STIX]{x1D703}}_{p}\Vert _{\unicode[STIX]{x1D6F4}_{p}^{-1}}^{2}\biggr).\end{eqnarray}$$
In this case, the maximum a posteriori estimator is
 $$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D703}}_{\mathit{MAP}}=\arg \min _{\boldsymbol{\unicode[STIX]{x1D703}}\in \mathbb{R}^{p}}\biggl(\frac{1}{2}\Vert \boldsymbol{z}-\boldsymbol{f}(\boldsymbol{\unicode[STIX]{x1D703}})\Vert _{\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D700}}^{-1}}^{2}+\frac{1}{2}\Vert \boldsymbol{\unicode[STIX]{x1D703}}-\boldsymbol{\unicode[STIX]{x1D703}}_{p}\Vert _{\unicode[STIX]{x1D6F4}_{p}^{-1}}^{2}\biggr),\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D703}}_{\mathit{MAP}}=\arg \min _{\boldsymbol{\unicode[STIX]{x1D703}}\in \mathbb{R}^{p}}\biggl(\frac{1}{2}\Vert \boldsymbol{z}-\boldsymbol{f}(\boldsymbol{\unicode[STIX]{x1D703}})\Vert _{\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D700}}^{-1}}^{2}+\frac{1}{2}\Vert \boldsymbol{\unicode[STIX]{x1D703}}-\boldsymbol{\unicode[STIX]{x1D703}}_{p}\Vert _{\unicode[STIX]{x1D6F4}_{p}^{-1}}^{2}\biggr),\end{eqnarray}$$
that is, it coincides with the estimator obtained by solving the (static version, with
![]() $K=1$
of the) regularized least-squares problem (10.4), as long as we choose
$K=1$
of the) regularized least-squares problem (10.4), as long as we choose
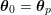 $\boldsymbol{\unicode[STIX]{x1D703}}_{0}=\boldsymbol{\unicode[STIX]{x1D703}}_{p}$
,
$\boldsymbol{\unicode[STIX]{x1D703}}_{0}=\boldsymbol{\unicode[STIX]{x1D703}}_{p}$
,
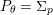 $P_{\unicode[STIX]{x1D703}}=\unicode[STIX]{x1D6F4}_{p}$
and
$P_{\unicode[STIX]{x1D703}}=\unicode[STIX]{x1D6F4}_{p}$
and
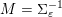 $M=\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D700}}^{-1}$
. If we assume instead that no information is available about the parameter distribution except that it resides in a subset
$M=\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D700}}^{-1}$
. If we assume instead that no information is available about the parameter distribution except that it resides in a subset
![]() ${\mathcal{D}}$
of the parameter space
${\mathcal{D}}$
of the parameter space
![]() $\mathbb{R}^{p}$
, then
$\mathbb{R}^{p}$
, then
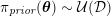 $\unicode[STIX]{x1D70B}_{\mathit{prior}}(\boldsymbol{\unicode[STIX]{x1D703}})\sim {\mathcal{U}}({\mathcal{D}})$
is a uniform distribution over
$\unicode[STIX]{x1D70B}_{\mathit{prior}}(\boldsymbol{\unicode[STIX]{x1D703}})\sim {\mathcal{U}}({\mathcal{D}})$
is a uniform distribution over
![]() ${\mathcal{D}}$
.
${\mathcal{D}}$
.
Remark 11.1. Note that the parameter estimation techniques of Section 10.1 can be seen as strategies yielding point estimates without any reference to underlying statistical models. However, when a Gaussian assumption is made in the Bayesian framework, the regularization term and the norms
![]() $\Vert \cdot \Vert _{\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D700}}^{-1}}$
,
$\Vert \cdot \Vert _{\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D700}}^{-1}}$
,
![]() $\Vert \cdot \Vert _{\unicode[STIX]{x1D6F4}_{p}^{-1}}$
and the value
$\Vert \cdot \Vert _{\unicode[STIX]{x1D6F4}_{p}^{-1}}$
and the value
![]() $\boldsymbol{\unicode[STIX]{x1D703}}_{p}$
have a clear interpretation in terms of measurement noise and prior probability distribution. Hence, a prior that carries sufficient information about the true underlying structure of the parameters often provides more meaningful estimates and regularizes the inverse problem in a more natural way than relying on abstract regularization terms, as in (10.4), that might not have any interpretation. The benefit of casting parameter estimation problems in the form of inverse UQ problems is that one is also able to characterize the variance of the prediction due to measurement and model errors more precisely than from the single-point estimates.
$\boldsymbol{\unicode[STIX]{x1D703}}_{p}$
have a clear interpretation in terms of measurement noise and prior probability distribution. Hence, a prior that carries sufficient information about the true underlying structure of the parameters often provides more meaningful estimates and regularizes the inverse problem in a more natural way than relying on abstract regularization terms, as in (10.4), that might not have any interpretation. The benefit of casting parameter estimation problems in the form of inverse UQ problems is that one is also able to characterize the variance of the prediction due to measurement and model errors more precisely than from the single-point estimates.
Exploring the posterior distribution in the case where the input space
![]() ${\mathcal{D}}$
has a larger dimension than
${\mathcal{D}}$
has a larger dimension than
![]() $p=2$
or
$p=2$
or
![]() $3$
calls into play suitable sampling methods, among which the Markov chain Monte Carlo (MCMC) techniques are the most relevant example. Instead of evaluating the posterior PDF at a single point, an MCMC technique is a systematic way to generate a sample which can be used to explore the distribution, as well as to perform Monte Carlo integration as in (11.1) in order to compute the conditional mean or conditional covariance, for example. In the former case, the posterior
$3$
calls into play suitable sampling methods, among which the Markov chain Monte Carlo (MCMC) techniques are the most relevant example. Instead of evaluating the posterior PDF at a single point, an MCMC technique is a systematic way to generate a sample which can be used to explore the distribution, as well as to perform Monte Carlo integration as in (11.1) in order to compute the conditional mean or conditional covariance, for example. In the former case, the posterior
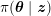 $\unicode[STIX]{x1D70B}(\boldsymbol{\unicode[STIX]{x1D703}}\mid \boldsymbol{z})$
plays the role of target probability distribution that we want to explore, and is obtained as a realization of a Markov chain by relying on the following Metropolis–Hastings algorithm, for example.
$\unicode[STIX]{x1D70B}(\boldsymbol{\unicode[STIX]{x1D703}}\mid \boldsymbol{z})$
plays the role of target probability distribution that we want to explore, and is obtained as a realization of a Markov chain by relying on the following Metropolis–Hastings algorithm, for example.
-
(1) Pick an initial
 $\boldsymbol{\unicode[STIX]{x1D703}}_{1}$
.
$\boldsymbol{\unicode[STIX]{x1D703}}_{1}$
. -
(2) For
 $m=1,\ldots ,M$
:
$m=1,\ldots ,M$
:-
(a) Compute
 $\unicode[STIX]{x1D70B}(\boldsymbol{\unicode[STIX]{x1D703}}^{m}\mid \boldsymbol{z})$
.
$\unicode[STIX]{x1D70B}(\boldsymbol{\unicode[STIX]{x1D703}}^{m}\mid \boldsymbol{z})$
. -
(b) Draw
 $\boldsymbol{w}\sim {\mathcal{N}}(\mathbf{0},\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D700}})$
and take a random step to find the next candidate
$\boldsymbol{w}\sim {\mathcal{N}}(\mathbf{0},\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D700}})$
and take a random step to find the next candidate
 $\widehat{\boldsymbol{\unicode[STIX]{x1D703}}}=\boldsymbol{\unicode[STIX]{x1D703}}_{k}+\boldsymbol{w}$
.
$\widehat{\boldsymbol{\unicode[STIX]{x1D703}}}=\boldsymbol{\unicode[STIX]{x1D703}}_{k}+\boldsymbol{w}$
. -
(c) Compute
 $\unicode[STIX]{x1D70B}(\widehat{\boldsymbol{\unicode[STIX]{x1D703}}}\mid \boldsymbol{z})$
.
$\unicode[STIX]{x1D70B}(\widehat{\boldsymbol{\unicode[STIX]{x1D703}}}\mid \boldsymbol{z})$
. -
(d) Define the acceptance ratio
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{m}=\min \biggl\{1,\displaystyle \frac{\unicode[STIX]{x1D70B}(\widehat{\boldsymbol{\unicode[STIX]{x1D703}}}\mid \boldsymbol{z})}{\unicode[STIX]{x1D70B}(\boldsymbol{\unicode[STIX]{x1D703}}_{m}\mid \boldsymbol{z})}\biggr\}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{m}=\min \biggl\{1,\displaystyle \frac{\unicode[STIX]{x1D70B}(\widehat{\boldsymbol{\unicode[STIX]{x1D703}}}\mid \boldsymbol{z})}{\unicode[STIX]{x1D70B}(\boldsymbol{\unicode[STIX]{x1D703}}_{m}\mid \boldsymbol{z})}\biggr\}.\end{eqnarray}$$
-
(e) Let
 $u\sim {\mathcal{U}}([0,1])$
. If
$u\sim {\mathcal{U}}([0,1])$
. If
 $u\leq \unicode[STIX]{x1D6FC}_{m}$
, accept, set
$u\leq \unicode[STIX]{x1D6FC}_{m}$
, accept, set
 $\boldsymbol{\unicode[STIX]{x1D703}}_{m+1}=\widehat{\boldsymbol{\unicode[STIX]{x1D703}}}$
, and add to the set of samples
$\boldsymbol{\unicode[STIX]{x1D703}}_{m+1}=\widehat{\boldsymbol{\unicode[STIX]{x1D703}}}$
, and add to the set of samples
 $\unicode[STIX]{x1D6EF}$
; otherwise reject, and keep
$\unicode[STIX]{x1D6EF}$
; otherwise reject, and keep
 $\boldsymbol{\unicode[STIX]{x1D703}}_{m+1}=\boldsymbol{\unicode[STIX]{x1D703}}_{m}$
.
$\boldsymbol{\unicode[STIX]{x1D703}}_{m+1}=\boldsymbol{\unicode[STIX]{x1D703}}_{m}$
.
-
After
![]() $M$
steps of the algorithm, the set
$M$
steps of the algorithm, the set
![]() $\unicode[STIX]{x1D6EF}$
of samples contains realizations of the probability distribution
$\unicode[STIX]{x1D6EF}$
of samples contains realizations of the probability distribution
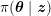 $\unicode[STIX]{x1D70B}(\boldsymbol{\unicode[STIX]{x1D703}}\mid \boldsymbol{z})$
. The random step in point (b) from the current sample to the next candidate is distributed as white noise; its covariance should be chosen as large as possible while still maintaining a reasonable acceptance rate. Moreover, the initial points of the generated set usually represent the distribution to be explored poorly, and are then removed from the sample. To learn more on MCMC algorithms we refer to Kaipio and Somersalo (Reference Kaipio and Somersalo2005), Robert and Casella (Reference Robert and Casella2004) and Voss (Reference Voss2013), and references therein.
$\unicode[STIX]{x1D70B}(\boldsymbol{\unicode[STIX]{x1D703}}\mid \boldsymbol{z})$
. The random step in point (b) from the current sample to the next candidate is distributed as white noise; its covariance should be chosen as large as possible while still maintaining a reasonable acceptance rate. Moreover, the initial points of the generated set usually represent the distribution to be explored poorly, and are then removed from the sample. To learn more on MCMC algorithms we refer to Kaipio and Somersalo (Reference Kaipio and Somersalo2005), Robert and Casella (Reference Robert and Casella2004) and Voss (Reference Voss2013), and references therein.
11.2.2 Dynamical problems
Backward UQ problems whose forward system is stationary, or with observations that are not acquired sequentially in time, can be cast in the form of a Bayesian inverse problem, as shown in the previous section. In these cases, backward UQ can be formulated in the Bayesian framework by means of Bayesian filtering methods, among which the Kalman filter can be seen as a particular instance. These problems are also referred to as non-stationary inverse problems. As in Section 10.2, depending on the quantities that have to be estimated, the problem can be formulated as a state estimation or a joint state/parameter estimation problem. We will treat both these cases but will limit our discussion to finite-dimensional models (which usually arise from space and time discretization of unsteady PDEs) and using time-discretized evolution models. Further discussion can be found in Kaipio and Somersalo (Reference Kaipio and Somersalo2005), Särkkä (Reference Särkkä2013), Sullivan (Reference Sullivan2015) and Houtemaker and Zhang (Reference Houtemaker and Zhang2016), for example.
Let
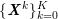 $\{\boldsymbol{X}^{k}\}_{k=0}^{K}$
and
$\{\boldsymbol{X}^{k}\}_{k=0}^{K}$
and
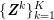 $\{\boldsymbol{Z}^{k}\}_{k=1}^{K}$
denote two stochastic processes; the former is related to the quantity we are interested in, whereas the latter represents the measurement. In particular, the random vector
$\{\boldsymbol{Z}^{k}\}_{k=1}^{K}$
denote two stochastic processes; the former is related to the quantity we are interested in, whereas the latter represents the measurement. In particular, the random vector
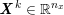 $\boldsymbol{X}^{k}\in \mathbb{R}^{n_{x}}$
is referred to as the state vector, whereas the random vector
$\boldsymbol{X}^{k}\in \mathbb{R}^{n_{x}}$
is referred to as the state vector, whereas the random vector
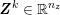 $\boldsymbol{Z}^{k}\in \mathbb{R}^{n_{z}}$
is referred to as the observation, both considered at the
$\boldsymbol{Z}^{k}\in \mathbb{R}^{n_{z}}$
is referred to as the observation, both considered at the
![]() $k$
th time
$k$
th time
![]() $\unicode[STIX]{x1D70F}^{k}$
. From a Bayesian standpoint, the goal is to use the observations until time
$\unicode[STIX]{x1D70F}^{k}$
. From a Bayesian standpoint, the goal is to use the observations until time
![]() $k$
to get information about the state
$k$
to get information about the state
![]() $\boldsymbol{X}^{k}$
and quantify the uncertainty related to this estimate. To frame this problem in the Bayesian setting, we assume that
$\boldsymbol{X}^{k}$
and quantify the uncertainty related to this estimate. To frame this problem in the Bayesian setting, we assume that
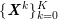 $\{\boldsymbol{X}^{k}\}_{k=0}^{K}$
and
$\{\boldsymbol{X}^{k}\}_{k=0}^{K}$
and
 $\{\boldsymbol{Z}^{k}\}_{k=1}^{K}$
are an evolution/observation model, as follows.
$\{\boldsymbol{Z}^{k}\}_{k=1}^{K}$
are an evolution/observation model, as follows.
-
(1)
 $\{\boldsymbol{X}^{k}\}_{k=0}^{K}$
and
$\{\boldsymbol{X}^{k}\}_{k=0}^{K}$
and
 $\{\boldsymbol{Z}^{k}\}_{k=1}^{K}$
are Markov processes, that is,
$\{\boldsymbol{Z}^{k}\}_{k=1}^{K}$
are Markov processes, that is,  $$\begin{eqnarray}\displaystyle \begin{array}{@{}ll@{}}\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k+1}\mid \boldsymbol{x}^{0},\boldsymbol{x}^{1},\ldots ,\boldsymbol{x}^{k})=\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k+1}\mid \boldsymbol{x}^{k}), & \quad k=0,1,\ldots ,\\ \unicode[STIX]{x1D70B}(\boldsymbol{z}^{k}\mid \boldsymbol{x}^{0},\boldsymbol{x}^{1},\ldots ,\boldsymbol{x}^{k})=\unicode[STIX]{x1D70B}(\boldsymbol{z}^{k}\mid \boldsymbol{x}^{k}), & \quad k=1,2,\ldots .\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}ll@{}}\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k+1}\mid \boldsymbol{x}^{0},\boldsymbol{x}^{1},\ldots ,\boldsymbol{x}^{k})=\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k+1}\mid \boldsymbol{x}^{k}), & \quad k=0,1,\ldots ,\\ \unicode[STIX]{x1D70B}(\boldsymbol{z}^{k}\mid \boldsymbol{x}^{0},\boldsymbol{x}^{1},\ldots ,\boldsymbol{x}^{k})=\unicode[STIX]{x1D70B}(\boldsymbol{z}^{k}\mid \boldsymbol{x}^{k}), & \quad k=1,2,\ldots .\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
-
(2)
 $\{\boldsymbol{X}^{k}\}_{k=0}^{K}$
depends on the past observations only through its own history, that is,
$\{\boldsymbol{X}^{k}\}_{k=0}^{K}$
depends on the past observations only through its own history, that is,  $$\begin{eqnarray}\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k+1}\mid \boldsymbol{x}^{k},\boldsymbol{z}^{1},\ldots ,\boldsymbol{z}^{k})=\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k+1}\mid \boldsymbol{z}^{k}),\quad k=0,1,\ldots .\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k+1}\mid \boldsymbol{x}^{k},\boldsymbol{z}^{1},\ldots ,\boldsymbol{z}^{k})=\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k+1}\mid \boldsymbol{z}^{k}),\quad k=0,1,\ldots .\end{eqnarray}$$
Here
![]() $\boldsymbol{x}^{k}$
,
$\boldsymbol{x}^{k}$
,
![]() $\boldsymbol{z}^{k}$
denote the realizations of the processes
$\boldsymbol{z}^{k}$
denote the realizations of the processes
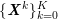 $\{\boldsymbol{X}^{k}\}_{k=0}^{K}$
and
$\{\boldsymbol{X}^{k}\}_{k=0}^{K}$
and
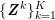 $\{\boldsymbol{Z}^{k}\}_{k=1}^{K}$
, respectively. In order to characterize such a model, we need to specify the PDF of the initial state
$\{\boldsymbol{Z}^{k}\}_{k=1}^{K}$
, respectively. In order to characterize such a model, we need to specify the PDF of the initial state
![]() $\boldsymbol{X}^{0}$
,
$\boldsymbol{X}^{0}$
,
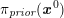 $\unicode[STIX]{x1D70B}_{\mathit{prior}}(\boldsymbol{x}^{0})$
, the so-called transition kernel
$\unicode[STIX]{x1D70B}_{\mathit{prior}}(\boldsymbol{x}^{0})$
, the so-called transition kernel
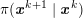 $\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k+1}\mid \boldsymbol{x}^{k})$
,
$\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k+1}\mid \boldsymbol{x}^{k})$
,
 $k=0,1,\ldots$
and the conditional probability
$k=0,1,\ldots$
and the conditional probability
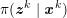 $\unicode[STIX]{x1D70B}(\boldsymbol{z}^{k}\mid \boldsymbol{x}^{k})$
,
$\unicode[STIX]{x1D70B}(\boldsymbol{z}^{k}\mid \boldsymbol{x}^{k})$
,
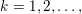 $k=1,2,\ldots ,$
the so-called (conditional) likelihood function. We assume a state evolution equation of the form
$k=1,2,\ldots ,$
the so-called (conditional) likelihood function. We assume a state evolution equation of the form
 $$\begin{eqnarray}\boldsymbol{X}^{k+1}=\boldsymbol{f}^{k+1}(\boldsymbol{X}^{k},\boldsymbol{V}^{k+1}),\quad k=0,1,\ldots\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{X}^{k+1}=\boldsymbol{f}^{k+1}(\boldsymbol{X}^{k},\boldsymbol{V}^{k+1}),\quad k=0,1,\ldots\end{eqnarray}$$
and an observation equation of the form
 $$\begin{eqnarray}\boldsymbol{Z}^{k}=\boldsymbol{h}^{k}(\boldsymbol{X}^{k},\boldsymbol{W}^{k}),\quad k=1,2,\ldots .\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{Z}^{k}=\boldsymbol{h}^{k}(\boldsymbol{X}^{k},\boldsymbol{W}^{k}),\quad k=1,2,\ldots .\end{eqnarray}$$
Here
![]() $\boldsymbol{f}^{k+1}$
and
$\boldsymbol{f}^{k+1}$
and
![]() $\boldsymbol{h}^{k}$
are known functions, whereas
$\boldsymbol{h}^{k}$
are known functions, whereas
 $\boldsymbol{V}^{k+1}\in \mathbb{R}^{n_{x}}$
and
$\boldsymbol{V}^{k+1}\in \mathbb{R}^{n_{x}}$
and
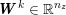 $\boldsymbol{W}^{k}\in \mathbb{R}^{n_{z}}$
denote the state noise and the observation noise, respectively. We want to determine the conditional PDF
$\boldsymbol{W}^{k}\in \mathbb{R}^{n_{z}}$
denote the state noise and the observation noise, respectively. We want to determine the conditional PDF
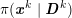 $\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k}\mid \boldsymbol{D}^{k})$
of the state at the
$\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k}\mid \boldsymbol{D}^{k})$
of the state at the
![]() $k$
th time instant given the observations
$k$
th time instant given the observations
 $\boldsymbol{D}^{k}=(\boldsymbol{z}^{1},\ldots ,\boldsymbol{z}^{k})$
up to the same time instant; this procedure is usually referred to as filtering problem. By recursive application of Bayes’ theorem, we have the following.
$\boldsymbol{D}^{k}=(\boldsymbol{z}^{1},\ldots ,\boldsymbol{z}^{k})$
up to the same time instant; this procedure is usually referred to as filtering problem. By recursive application of Bayes’ theorem, we have the following.
-
∙ The time evolution updating, i.e., the problem of determining
 $\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k+1}\mid \boldsymbol{D}^{k})$
given
$\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k+1}\mid \boldsymbol{D}^{k})$
given
 $\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k}\mid \boldsymbol{D}^{k})$
and the transition kernel
$\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k}\mid \boldsymbol{D}^{k})$
and the transition kernel
 $\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k+1}\mid \boldsymbol{x}^{k})$
, provides (11.5)
$\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k+1}\mid \boldsymbol{x}^{k})$
, provides (11.5) $$\begin{eqnarray}\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k+1}\mid \boldsymbol{D}^{k})=\int _{\mathbb{ R}^{n_{x}}}\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k+1}\mid \boldsymbol{x}^{k})\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k}\mid \boldsymbol{D}^{k})\text{d}\boldsymbol{x}^{k}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k+1}\mid \boldsymbol{D}^{k})=\int _{\mathbb{ R}^{n_{x}}}\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k+1}\mid \boldsymbol{x}^{k})\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k}\mid \boldsymbol{D}^{k})\text{d}\boldsymbol{x}^{k}.\end{eqnarray}$$
-
∙ The observation updating, i.e., the problem of determining the posterior distribution
 $\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k+1}\mid \boldsymbol{D}^{k+1})$
of
$\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k+1}\mid \boldsymbol{D}^{k+1})$
of
 $\boldsymbol{X}^{k}\mid \boldsymbol{D}^{k}$
based on the new observation
$\boldsymbol{X}^{k}\mid \boldsymbol{D}^{k}$
based on the new observation
 $\boldsymbol{Z}^{k+1}$
given
$\boldsymbol{Z}^{k+1}$
given
 $\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k+1}\mid \boldsymbol{D}^{k})$
and the likelihood function
$\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k+1}\mid \boldsymbol{D}^{k})$
and the likelihood function
 $\unicode[STIX]{x1D70B}(\boldsymbol{z}^{k+1}\mid \boldsymbol{x}^{k+1})$
, provides (11.6)where
$\unicode[STIX]{x1D70B}(\boldsymbol{z}^{k+1}\mid \boldsymbol{x}^{k+1})$
, provides (11.6)where $$\begin{eqnarray}\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k+1}\mid \boldsymbol{D}^{k+1})=\frac{\unicode[STIX]{x1D70B}(\boldsymbol{z}^{k+1}\mid \boldsymbol{x}^{k+1})\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k+1}\mid \boldsymbol{D}^{k})}{\unicode[STIX]{x1D70B}(\boldsymbol{z}^{k+1}\mid \boldsymbol{D}^{k})},\end{eqnarray}$$
Formula (11.6) is Bayes’ formula, where
$$\begin{eqnarray}\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k+1}\mid \boldsymbol{D}^{k+1})=\frac{\unicode[STIX]{x1D70B}(\boldsymbol{z}^{k+1}\mid \boldsymbol{x}^{k+1})\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k+1}\mid \boldsymbol{D}^{k})}{\unicode[STIX]{x1D70B}(\boldsymbol{z}^{k+1}\mid \boldsymbol{D}^{k})},\end{eqnarray}$$
Formula (11.6) is Bayes’ formula, where $$\begin{eqnarray}\unicode[STIX]{x1D70B}(\boldsymbol{z}^{k+1}\mid \boldsymbol{D}^{k})=\int _{\mathbb{ R}^{n_{x}}}\unicode[STIX]{x1D70B}(\boldsymbol{z}^{k+1}\mid \boldsymbol{x}^{k+1})\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k+1}\mid \boldsymbol{D}^{k})\text{d}\boldsymbol{x}^{k+1}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}(\boldsymbol{z}^{k+1}\mid \boldsymbol{D}^{k})=\int _{\mathbb{ R}^{n_{x}}}\unicode[STIX]{x1D70B}(\boldsymbol{z}^{k+1}\mid \boldsymbol{x}^{k+1})\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k+1}\mid \boldsymbol{D}^{k})\text{d}\boldsymbol{x}^{k+1}.\end{eqnarray}$$
 $\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k+1}\mid \boldsymbol{D}^{k})$
is considered as the prior distribution for
$\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k+1}\mid \boldsymbol{D}^{k})$
is considered as the prior distribution for
 $\boldsymbol{x}^{k+1}$
.
$\boldsymbol{x}^{k+1}$
.
The Kalman filter introduced in Section 10.2.1 is a remarkable instance of Bayesian filter method. Indeed, let us assume that the state and the observation equations are linear with additive noise processes, that is,
 $$\begin{eqnarray}\boldsymbol{f}^{k+1}(\boldsymbol{x}^{k},\boldsymbol{v}^{k})=A_{k|k+1}\boldsymbol{x}^{k}+\boldsymbol{v}^{k},\quad \boldsymbol{h}^{k}=H_{k}\boldsymbol{x}^{k}+\boldsymbol{w}^{k},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{f}^{k+1}(\boldsymbol{x}^{k},\boldsymbol{v}^{k})=A_{k|k+1}\boldsymbol{x}^{k}+\boldsymbol{v}^{k},\quad \boldsymbol{h}^{k}=H_{k}\boldsymbol{x}^{k}+\boldsymbol{w}^{k},\end{eqnarray}$$
for given matrices
![]() $A_{k|k+1}$
,
$A_{k|k+1}$
,
![]() $H_{k}$
, that the noise vectors
$H_{k}$
, that the noise vectors
![]() $\boldsymbol{V}^{k+1}$
and
$\boldsymbol{V}^{k+1}$
and
![]() $\boldsymbol{W}^{k}$
are mutually independent, Gaussian, with zero mean and known covariances
$\boldsymbol{W}^{k}$
are mutually independent, Gaussian, with zero mean and known covariances
![]() $Q_{k+1}$
and
$Q_{k+1}$
and
![]() $R_{k}$
, respectively, and that the prior PDF of
$R_{k}$
, respectively, and that the prior PDF of
![]() $\boldsymbol{X}^{0}$
is Gaussian with mean
$\boldsymbol{X}^{0}$
is Gaussian with mean
![]() $\boldsymbol{m}^{0}$
and covariance
$\boldsymbol{m}^{0}$
and covariance
![]() $P^{0}$
. Under these assumptions, the time evolution and the observation updating formulas (11.3, 11.4) involve Gaussian distributions, whose means and covariances can be updated at each step according to prediction formulas (10.15a
, 10.15b
) and correction formulas (10.15d
, 10.15e
), respectively. In particular, we have that
$P^{0}$
. Under these assumptions, the time evolution and the observation updating formulas (11.3, 11.4) involve Gaussian distributions, whose means and covariances can be updated at each step according to prediction formulas (10.15a
, 10.15b
) and correction formulas (10.15d
, 10.15e
), respectively. In particular, we have that
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70B}(\boldsymbol{x}^{k+1}\mid \boldsymbol{x}^{k}) & \displaystyle \sim N(A_{k|k+1}\boldsymbol{x}^{k},Q^{k}),\nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D70B}(\boldsymbol{z}^{k}\mid \boldsymbol{x}^{k}) & \displaystyle \sim N(H_{k}\boldsymbol{x}^{k},R_{k}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70B}(\boldsymbol{x}^{k+1}\mid \boldsymbol{x}^{k}) & \displaystyle \sim N(A_{k|k+1}\boldsymbol{x}^{k},Q^{k}),\nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D70B}(\boldsymbol{z}^{k}\mid \boldsymbol{x}^{k}) & \displaystyle \sim N(H_{k}\boldsymbol{x}^{k},R_{k}).\nonumber\end{eqnarray}$$
The Bayesian filtering equations can be evaluated in closed form, yielding the following Gaussian distributions:
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70B}(\boldsymbol{x}^{k}\mid \boldsymbol{D}^{k-1}) & \displaystyle \sim {\mathcal{N}}(\boldsymbol{m}_{f}^{k},P_{k}^{f}),\nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D70B}(\boldsymbol{x}^{k}\mid \boldsymbol{D}^{k}) & \displaystyle \sim {\mathcal{N}}(\boldsymbol{m}_{a}^{k},P_{k}^{a}),\nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D70B}(\boldsymbol{z}^{k}\mid \boldsymbol{D}^{k-1}) & \displaystyle \sim {\mathcal{N}}(H_{k}\boldsymbol{m}_{f}^{k},H_{k}P_{k}^{f}H_{k}^{T}+R_{k}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70B}(\boldsymbol{x}^{k}\mid \boldsymbol{D}^{k-1}) & \displaystyle \sim {\mathcal{N}}(\boldsymbol{m}_{f}^{k},P_{k}^{f}),\nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D70B}(\boldsymbol{x}^{k}\mid \boldsymbol{D}^{k}) & \displaystyle \sim {\mathcal{N}}(\boldsymbol{m}_{a}^{k},P_{k}^{a}),\nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D70B}(\boldsymbol{z}^{k}\mid \boldsymbol{D}^{k-1}) & \displaystyle \sim {\mathcal{N}}(H_{k}\boldsymbol{m}_{f}^{k},H_{k}P_{k}^{f}H_{k}^{T}+R_{k}),\nonumber\end{eqnarray}$$
where the means and the variances can be computed with the Kalman filter prediction step
 $$\begin{eqnarray}\begin{array}{@{}l@{}}\displaystyle \boldsymbol{m}_{f}^{k}=A_{k-1|k}\boldsymbol{m}^{k-1},\\ \displaystyle P_{k}^{f}=A_{k-1|k}P_{k-1}^{a}A_{k-1|k}^{T}+Q_{k-1}\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}l@{}}\displaystyle \boldsymbol{m}_{f}^{k}=A_{k-1|k}\boldsymbol{m}^{k-1},\\ \displaystyle P_{k}^{f}=A_{k-1|k}P_{k-1}^{a}A_{k-1|k}^{T}+Q_{k-1}\end{array}\end{eqnarray}$$
and the consequent correction step
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}l@{}}\displaystyle K_{k}=P_{k}^{f}H_{k}^{T}(H_{k}P_{k}^{f}H_{k}^{T}+R_{k})^{-1},\\ \displaystyle \boldsymbol{m}_{a}^{k}=\boldsymbol{m}_{f}^{k}+F_{k}(\boldsymbol{z}^{k}-H_{k}\boldsymbol{m}_{f}^{k}),\\ \displaystyle P_{k}^{a}=(I-K_{k}H_{k})P_{k}^{f}.\end{array} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}l@{}}\displaystyle K_{k}=P_{k}^{f}H_{k}^{T}(H_{k}P_{k}^{f}H_{k}^{T}+R_{k})^{-1},\\ \displaystyle \boldsymbol{m}_{a}^{k}=\boldsymbol{m}_{f}^{k}+F_{k}(\boldsymbol{z}^{k}-H_{k}\boldsymbol{m}_{f}^{k}),\\ \displaystyle P_{k}^{a}=(I-K_{k}H_{k})P_{k}^{f}.\end{array} & & \displaystyle\end{eqnarray}$$
In other words, under the Gaussian assumption, the density is updated only through the mean and the covariance. A similar interpretation also holds for the EKF, as soon as a Gaussian approximation of the densities is considered, and the evolution of these densities is taken into account. In this respect, Bayesian filtering can be seen as a generalization of deterministic filters, such as the KF, EKF and UKF introduced in Section 10.2.
As already remarked in Section 10.2.2, when the evolution model is fully non-linear, the EKF, which can be seen as a particular instance of an approximate Gaussian filter, may perform badly: this can be explained by considering that the push-forward of the previous state estimate (which has a Gaussian distribution) by a non-linear map is poorly approximated by a Gaussian distribution. To avoid the linearization of the evolution and the observation models, one can rely on Monte Carlo methods to simulate the distributions by random samples, similarly to what has been done in the static case. This strategy yields the so-called particle filters (also referred to as sequential Monte Carlo methods), now very popular for complex backward UQ problems.
The goal of a particle filter is to produce an ensemble
 $\{\boldsymbol{x}_{1}^{k|k},\ldots ,\boldsymbol{x}_{N_{e}}^{k|k}\}$
of
$\{\boldsymbol{x}_{1}^{k|k},\ldots ,\boldsymbol{x}_{N_{e}}^{k|k}\}$
of
![]() $N_{e}$
particles sequentially, that is, a random sample distributed according to the conditional probability distribution
$N_{e}$
particles sequentially, that is, a random sample distributed according to the conditional probability distribution
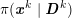 $\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k}\mid \boldsymbol{D}^{k})$
. The ensemble Kalman filter (EnKF), introduced by Evensen Reference Evensen1994, Reference Evensen2003, is a particle filter exploiting the idea of approximating the means and the covariances of the current estimate involved in the Kalman filter prediction-correction strategy by a set of particles sampled from the distribution. Unlike the Kalman filter itself, we evaluate the error covariance predictions and corrections by the ensemble covariance matrices around the corresponding ensemble mean, instead of classical covariance equations (10.15b
–10.15e
) given in the KF algorithm. The covariance matrices of the state vector
$\unicode[STIX]{x1D70B}(\boldsymbol{x}^{k}\mid \boldsymbol{D}^{k})$
. The ensemble Kalman filter (EnKF), introduced by Evensen Reference Evensen1994, Reference Evensen2003, is a particle filter exploiting the idea of approximating the means and the covariances of the current estimate involved in the Kalman filter prediction-correction strategy by a set of particles sampled from the distribution. Unlike the Kalman filter itself, we evaluate the error covariance predictions and corrections by the ensemble covariance matrices around the corresponding ensemble mean, instead of classical covariance equations (10.15b
–10.15e
) given in the KF algorithm. The covariance matrices of the state vector
![]() $\boldsymbol{X}$
need not be evolved, thus eliminating the costs associated with storing, multiplying and inverting the matrices appearing in the equations (10.15b
–10.15e
).
$\boldsymbol{X}$
need not be evolved, thus eliminating the costs associated with storing, multiplying and inverting the matrices appearing in the equations (10.15b
–10.15e
).
The ensemble is initialized by drawing
![]() $N_{e}$
independent particles from, say, a Gaussian distribution with mean
$N_{e}$
independent particles from, say, a Gaussian distribution with mean
![]() $\boldsymbol{m}^{0}$
and covariance
$\boldsymbol{m}^{0}$
and covariance
![]() $P_{0}$
.
$P_{0}$
.
-
∙ At each prediction step, each particle is evolved using the Kalman filter prediction step,
if the system is linear, or $$\begin{eqnarray}\boldsymbol{x}_{e}^{k|k-1}=A_{k-1|k}\boldsymbol{x}_{e}^{k-1|k-1}+\boldsymbol{v}^{k-1}\end{eqnarray}$$
if the system is non-linear.
$$\begin{eqnarray}\boldsymbol{x}_{e}^{k|k-1}=A_{k-1|k}\boldsymbol{x}_{e}^{k-1|k-1}+\boldsymbol{v}^{k-1}\end{eqnarray}$$
if the system is non-linear. $$\begin{eqnarray}\boldsymbol{x}_{e}^{k|k-1}=\boldsymbol{f}^{k}(\boldsymbol{x}_{e}^{k-1|k-1},\boldsymbol{v}^{k-1})\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{x}_{e}^{k|k-1}=\boldsymbol{f}^{k}(\boldsymbol{x}_{e}^{k-1|k-1},\boldsymbol{v}^{k-1})\end{eqnarray}$$
-
∙ At each correction step, the observation
 $\boldsymbol{z}^{k}$
is replicated
$\boldsymbol{z}^{k}$
is replicated
 $N_{e}$
times, obtaining Then, the empirical mean
$N_{e}$
times, obtaining Then, the empirical mean $$\begin{eqnarray}\boldsymbol{d}_{e}^{k}=\boldsymbol{z}^{k}+\boldsymbol{\unicode[STIX]{x1D702}}_{e}^{k},\quad \boldsymbol{\unicode[STIX]{x1D702}}_{e}^{k}\sim N(\mathbf{0},R_{k}).\end{eqnarray}$$
and the empirical covariance
$$\begin{eqnarray}\boldsymbol{d}_{e}^{k}=\boldsymbol{z}^{k}+\boldsymbol{\unicode[STIX]{x1D702}}_{e}^{k},\quad \boldsymbol{\unicode[STIX]{x1D702}}_{e}^{k}\sim N(\mathbf{0},R_{k}).\end{eqnarray}$$
and the empirical covariance $$\begin{eqnarray}\bar{\boldsymbol{x}}_{e}^{k|k-1}=\frac{1}{N_{e}}\mathop{\sum }_{e=1}^{N_{e}}\boldsymbol{x}_{e}^{k|k-1}\end{eqnarray}$$
of the particles set
$$\begin{eqnarray}\bar{\boldsymbol{x}}_{e}^{k|k-1}=\frac{1}{N_{e}}\mathop{\sum }_{e=1}^{N_{e}}\boldsymbol{x}_{e}^{k|k-1}\end{eqnarray}$$
of the particles set $$\begin{eqnarray}C_{k|k-1}^{E}=\frac{1}{N_{e}-1}\mathop{\sum }_{e=1}^{N_{e}}(\boldsymbol{x}_{e}^{k|k-1}-\bar{\boldsymbol{x}}_{e}^{k|k-1})(\boldsymbol{x}_{e}^{k|k-1}-\bar{\boldsymbol{x}}_{e}^{k|k-1})^{T}\end{eqnarray}$$
$$\begin{eqnarray}C_{k|k-1}^{E}=\frac{1}{N_{e}-1}\mathop{\sum }_{e=1}^{N_{e}}(\boldsymbol{x}_{e}^{k|k-1}-\bar{\boldsymbol{x}}_{e}^{k|k-1})(\boldsymbol{x}_{e}^{k|k-1}-\bar{\boldsymbol{x}}_{e}^{k|k-1})^{T}\end{eqnarray}$$
 $\{\boldsymbol{x}_{e}^{k|k-1}\}_{e=1}^{N_{e}}$
are computed. The exact Kalman gain is then approximated by and, finally, the state correction is obtained by applying the formula (10.15d ) to each particle, that is,
$\{\boldsymbol{x}_{e}^{k|k-1}\}_{e=1}^{N_{e}}$
are computed. The exact Kalman gain is then approximated by and, finally, the state correction is obtained by applying the formula (10.15d ) to each particle, that is, $$\begin{eqnarray}K_{k}^{E}=C_{k|k-1}^{E}H_{k}^{T}(H_{k}C_{k|k-1}^{E}H_{k}^{T}+R_{k})^{-1}\end{eqnarray}$$
$$\begin{eqnarray}K_{k}^{E}=C_{k|k-1}^{E}H_{k}^{T}(H_{k}C_{k|k-1}^{E}H_{k}^{T}+R_{k})^{-1}\end{eqnarray}$$
 $$\begin{eqnarray}\boldsymbol{x}_{e}^{k|k}=\boldsymbol{x}_{e}^{k|k-1}+K_{k}^{E}(\boldsymbol{d}_{e}^{k}-H_{k}\boldsymbol{x}_{e}^{k|k-1}).\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{x}_{e}^{k|k}=\boldsymbol{x}_{e}^{k|k-1}+K_{k}^{E}(\boldsymbol{d}_{e}^{k}-H_{k}\boldsymbol{x}_{e}^{k|k-1}).\end{eqnarray}$$
Several alternative implementations can be found, for example in Evensen Reference Evensen1994, Reference Evensen2009; for more on the ensemble Kalman filter, see also Iglesias, Law and Stuart (Reference Iglesias, Law and Stuart2013), Kelly, Law and Stuart (Reference Kelly, Law and Stuart2014), Ernst, Sprungk and Starkloff (Reference Ernst, Sprungk and Starkloff2014) and Houtemaker and Zhang (Reference Houtemaker and Zhang2016).
If the backward UQ problem also involves random inputs (as in the case of model parameters
![]() $\boldsymbol{\unicode[STIX]{x1D703}}$
, which can also be time-varying), the problem of state estimation and parameter estimation simultaneously arises. Generally speaking, there is no unique optimal solution for this problem. Similarly to the state augmentation technique presented in Section 10.2, a possible way to face this problem is to treat the unknown parameters
$\boldsymbol{\unicode[STIX]{x1D703}}$
, which can also be time-varying), the problem of state estimation and parameter estimation simultaneously arises. Generally speaking, there is no unique optimal solution for this problem. Similarly to the state augmentation technique presented in Section 10.2, a possible way to face this problem is to treat the unknown parameters
![]() $\boldsymbol{\unicode[STIX]{x1D703}}$
as part of the state, and use conventional filtering technique to infer the parameter and state simultaneously. This strategy goes by the name of joint estimation: see e.g. Moradkhani et al. (Reference Moradkhani, Sorooshian, Gupta and Houser2005), Ching, Beck and Porter (Reference Ching, Beck and Porter2006) and Evensen (Reference Evensen2009) for more details. An example related to cardiovascular modelling where an EnKF can be exploited to deal with state and parameter estimation is addressed in Section 11.3.2.
$\boldsymbol{\unicode[STIX]{x1D703}}$
as part of the state, and use conventional filtering technique to infer the parameter and state simultaneously. This strategy goes by the name of joint estimation: see e.g. Moradkhani et al. (Reference Moradkhani, Sorooshian, Gupta and Houser2005), Ching, Beck and Porter (Reference Ching, Beck and Porter2006) and Evensen (Reference Evensen2009) for more details. An example related to cardiovascular modelling where an EnKF can be exploited to deal with state and parameter estimation is addressed in Section 11.3.2.
11.3 Applications to cardiovascular modelling
Until recently, UQ has not been a priority for cardiovascular modelling. Today, a growing number of works focus on both forward and inverse UQ problems, taking into account uncertainties related to (i) measurement errors in experimental data (also referred to as observational uncertainty), (ii) model parameters, which may result from observational uncertainty as well as from variability, or lack of information, (iii) boundary and/or initial conditions and, possibly, (iv) the computational model itself, because of model limitations (model uncertainty) or systematic approximation errors (which can be seen as a form of epistemic uncertainty) introduced, for example, when the original high-fidelity model is replaced by a cheaper surrogate model or a reduced-order model. The list of contributions we mention is inevitably incomplete.
The effect of uncertain parameters in one-dimensional models of the arterial network was first considered by Xiu and Sherwin (Reference Xiu and Sherwin2007), who exploited a high-order stochastic collocation method based on the generalized polynomial chaos expansion, combined with a discontinuous Galerkin spectral/hp element discretization in physical space, in order to analyse the effects of parametric uncertainties related to material properties and the initial cross-sectional area of the arterial vessel in pulse wave propagation, in a network of up to 37 vessels connected via 16 bifurcations. Chen, Quarteroni and Rozza (Reference Chen, Quarteroni and Rozza2013) have considered a more general setting, taking into account a wider network and many more sources of parametric uncertainties, including parameter-dependent boundary conditions in each distal boundary site and geometric parameters describing the cross-section area in each arterial segment. Similar problems, involving both sensitivity analysis and uncertainty propagation for networks built over patient-specific datasets, can be found in Leguy et al. (Reference Leguy, Bosboom, Belloum, Hoeks and van de Vosse2011), Huberts et al. Reference Huberts, de Jonge, van der Linden, Inda, Passera, Tordoir, van de Vosse and Bosboom2013a , Reference Huberts, de Jonge, van der Linden, Inda, Tordoir, van de Vosse and Bosboom2013b and Brault, Dumas and Lucor (Reference Brault, Dumas and Lucor2017).
The use of an adaptive stochastic collocation framework to deal with UQ in haemodynamic simulations has been considered by Sankaran and Marsden (Reference Sankaran and Marsden2011), who extract relevant haemodynamic features – and quantify their uncertainty – for two idealized problems, namely an abdominal aortic aneurysm and a carotid artery bifurcation, and for a patient-specific problem, a Fontan procedure for congenital heart defects. In the former case, for instance, the radius of the abdominal aortic aneurysm, the radius and inflow velocity of the carotid artery bifurcation, and the flow split of the left and right pulmonary arteries are treated as random variables, following either Gaussian or uniform distributions, to account for the uncertainty impact on blood flows described by three-dimensional Navier–Stokes equations with rigid walls in small arterial portions. More detailed versions of this methodology have recently been exploited by Sankaran, Grady and Taylor (Reference Sankaran, Grady and Taylor2015) and Sankaran et al. (Reference Sankaran, Kim, Choi and Taylor2016) to analyse the impact of geometric uncertainties (i.e. anatomic uncertainties resulting in errors in the reconstructed geometry) and physiological uncertainties (yielding errors in boundary conditions or blood viscosity) for the blood flow and pressures in the coronary arteries.
The problem of calibrating outflow boundary conditions of blood flow simulations in truncated arterial domains has been cast in a Bayesian framework by D’Elia and Veneziani (Reference D’Elia and Veneziani2013) and Perdikaris and Karniadakis (Reference Perdikaris and Karniadakis2015), with the goal of quantifying the uncertainty affecting velocity and flow-related variables of interest, all treated as random variables.
A complete uncertainty propagation pipeline from clinical data to computational results has been considered by Schiavazzi et al. (Reference Schiavazzi, Arbia, Baker, Hlavacek, Hsia, Marsden and Vignon-Clementel2016), focusing on an example of single ventricle palliation surgery. After determining the probability density functions of right pulmonary artery flow split and average pulmonary pressures from clinical measurements, Bayesian parameter estimation is carried out in order to characterize the distributions of boundary conditions yielding the observed flow splits and average pressure distributions. Then, uncertainties in the boundary conditions are propagated to simulation predictions by employing sparse grid stochastic collocation to statistically characterize model predictions of post-operative haemodynamics in models with and without pulmonary artery stenosis, in order to quantify the statistical variability in virtual surgery predictions. Finally, the impact of uncertainty on the optimal design of idealized bypass graft models has been considered by Sankaran and Marsden (Reference Sankaran and Marsden2010) and Lassila et al. Reference Lassila, Manzoni, Quarteroni and Rozza2013a , Reference Lassila, Manzoni, Quarteroni and Rozza2013b , for example.
Regarding cardiac electrophysiology, a systematic application of UQ techniques to the forward problem of electrocardiography (i.e. the characterization of the torso potential given the electrical conductivity inside the heart and the torso) has been considered by Geneser, Kirby and MacLeod (Reference Geneser, Kirby and Macleod2008), focusing on a simplified 2D configuration representing a geometric model of a slice through the human thorax. The forward UQ propagation problem yielding the standard deviation of the resulting stochastic torso potentials depending on several uncertainties affecting, for example, the electrical conductivities of the organs and the representation of cardiac sources, has been tackled by a stochastic Galerkin method based on the generalized polynomial chaos expansion. Model personalization in cardiac electrophysiology has been considered by Konukoglu et al. (Reference Konukoglu, Relan, Cilingir, Menze, Chinchapatnam, Jadidi, Cochet, Hocini, Delingette, Jaïs, Haïssaguerre, Ayache and Sermesant2011), who applied an efficient Bayesian method exploiting polynomial chaos and compressed sensing to an eikonal-diffusion model involving a large (
![]() ${>}10$
) number of parameters, by integrating uncertainty on data and parameters.
${>}10$
) number of parameters, by integrating uncertainty on data and parameters.
Johnstone et al. (Reference Johnstone, Chang, Bardenet, de Boer, Gavaghan, Pathmanathan, Clayton and Mirams2016) have addressed a UQ framework for cardiac action potential models, focusing on (i) the inverse UQ problem of inferring the maximal conductance of ionic channels from noisy experimental recordings, and (ii) the forward UQ problem of propagating the uncertainty in maximal ion channel conductances to suitable outputs of interest, such as the action potential duration. To solve the inverse UQ problem a Bayesian framework, such as that described in Section 11.2, has been successfully employed, whereas the UQ propagation problem has been tackled by means of a Monte Carlo approach exploiting suitable surrogate models, such as Gaussian process emulators, to speed up the evaluation of the system model under analysis. A detailed analysis of the mechanisms underlying physiological variability in cardiac electrophysiology and pro-arrhythmic risks under a variety of conditions can be found in Muszkiewicz et al. (Reference Muszkiewicz, Britton, Gemmell, Passini, Sánchez, Zhou, Carusi, Quinn, Burrage, Bueno-Orovio and Rodriguez2016).
Concerning heart electromechanics, Osnes and Sundnes (Reference Osnes and Sundnes2012) have addressed the quantification of the effect of uncertainties in the fibre orientation and the elasticity parameters included in the strain energy function on global output quantities such as the increase in cavity volume, the elongation of the ventricle, the increase in the inner radius, the decrease in wall thickness, and the rotation at the apex during the passive filling phase. Wallman, Smith and Rodriguez (Reference Wallman, Smith and Rodriguez2014) have estimated cardiac tissue properties by integrating structural information with electrophysiological data from electro-anatomical mapping systems, for example. By means of Bayesian inference tools, they obtained a simultaneous description of clinically relevant electrophysiological conduction properties and their associated uncertainty for various levels of noise, together with suitable design strategies to optimize the location and number of measurements required to maximize information and reduce uncertainty. A relevant application of UQ techniques to non-linear biomechanics has been considered by Biehler, Gee and Wall (Reference Biehler, Gee and Wall2015), where parametric uncertainties related to the constitutive law for the artery wall of an AAA are modelled as random fields. In particular, Biehler et al. use a lognormal three-dimensional random field to describe the inter- and intra-patient variations of one constitutive parameter of a hyperelastic constitutive model, and sampling-based approaches such as Monte Carlo to solve the resulting stochastic mechanical problem. A multi-fidelity Bayesian framework incorporating information from different low-fidelity models has been developed to speed up the intensive approximation of the resulting problem, following some general ideas reported by Kennedy and O’Hagan (Reference Kennedy and O’Hagan2000) and Koutsourelakis (Reference Koutsourelakis2009). Employment of surrogate models or more reliable reduced-order models (for more on this subject, see Section 12) to speed up the numerical solution of direct and inverse UQ problems is indeed a powerful alternative to stochastic collocation and stochastic Galerkin methods. However, they have only been partially touched on in the case of simple problems, for example in the works of Cui, Marzouk and Willcox (Reference Cui, Marzouk and Willcox2015), Chen and Schwab (Reference Chen and Schwab2015), Dihlmann and Haasdonk (Reference Dihlmann and Haasdonk2016), Manzoni, Pagani and Lassila (Reference Manzoni, Pagani and Lassila2016) and Pagani et al. (Reference Pagani, Manzoni and Quarteroni2016).
11.3.1 Backward uncertainty propagation in a simplified blood flow model

Figure 11.2. (a) Velocity profiles
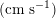 $(\text{cm}~\text{s}^{-1})$
for different carotid bifurcations parametrized with respect to the diameters
$(\text{cm}~\text{s}^{-1})$
for different carotid bifurcations parametrized with respect to the diameters
![]() $d_{c},d_{b}$
. (b) Variational parameter estimation and isolines of the pressure drop. (c) Two different choices of the prior distribution on diameters
$d_{c},d_{b}$
. (b) Variational parameter estimation and isolines of the pressure drop. (c) Two different choices of the prior distribution on diameters
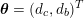 $\boldsymbol{\unicode[STIX]{x1D703}}=(d_{c},d_{b})^{T}$
. (d, e) Results of the backward UQ problem obtained with the priors in (c) with observed pressure drop
$\boldsymbol{\unicode[STIX]{x1D703}}=(d_{c},d_{b})^{T}$
. (d, e) Results of the backward UQ problem obtained with the priors in (c) with observed pressure drop
 $\boldsymbol{z}_{\mathit{obs}}=-1400$
and
$\boldsymbol{z}_{\mathit{obs}}=-1400$
and
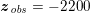 $\boldsymbol{z}_{\mathit{obs}}=-2200$
$\boldsymbol{z}_{\mathit{obs}}=-2200$
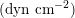 $(\text{dyn}~\text{cm}^{-2})$
, respectively. Numerical results were obtained using the MATLAB finite element library MLife.
$(\text{dyn}~\text{cm}^{-2})$
, respectively. Numerical results were obtained using the MATLAB finite element library MLife.
We want to compare the solution of a parameter estimation problem in a variational framework and in a Bayesian setting, on a simplified blood flow problem. We consider a two-dimensional section of a carotid artery bifurcation where the diameters
![]() $d_{c},d_{b}$
of the common carotid artery (CCA) at the bifurcation and of the mid-sinus level of the internal carotid artery (ICA) are the input parameters, assumed to be uncertain. In this idealized setting, our goal is to identify
$d_{c},d_{b}$
of the common carotid artery (CCA) at the bifurcation and of the mid-sinus level of the internal carotid artery (ICA) are the input parameters, assumed to be uncertain. In this idealized setting, our goal is to identify
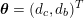 $\boldsymbol{\unicode[STIX]{x1D703}}=(d_{c},d_{b})^{T}$
from the observation of the mean pressure drop
$\boldsymbol{\unicode[STIX]{x1D703}}=(d_{c},d_{b})^{T}$
from the observation of the mean pressure drop
 $$\begin{eqnarray}\boldsymbol{z}=\frac{1}{|\unicode[STIX]{x1D6E4}_{\mathit{in}}|}\int _{\unicode[STIX]{x1D6E4}_{\mathit{in}}}p\text{d}\unicode[STIX]{x1D6FE}-\frac{1}{|\unicode[STIX]{x1D6E4}_{\mathit{ICA}}|}\int _{\unicode[STIX]{x1D6E4}_{\mathit{ICA}}}p\text{d}\unicode[STIX]{x1D6FE}\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{z}=\frac{1}{|\unicode[STIX]{x1D6E4}_{\mathit{in}}|}\int _{\unicode[STIX]{x1D6E4}_{\mathit{in}}}p\text{d}\unicode[STIX]{x1D6FE}-\frac{1}{|\unicode[STIX]{x1D6E4}_{\mathit{ICA}}|}\int _{\unicode[STIX]{x1D6E4}_{\mathit{ICA}}}p\text{d}\unicode[STIX]{x1D6FE}\end{eqnarray}$$
between the internal carotid outflow
![]() $\unicode[STIX]{x1D6E4}_{\mathit{ICA}}$
and the inflow
$\unicode[STIX]{x1D6E4}_{\mathit{ICA}}$
and the inflow
![]() $\unicode[STIX]{x1D6E4}_{\mathit{in}}$
: see Figure 11.2(a). For simplicity, a steady incompressible Navier–Stokes model is employed to model the blood flow, although the same approach concerning the solution of the inverse UQ problem can be applied to the case of an unsteady fluid model, as soon as a peak (or time average) pressure drop is evaluated. Although presented here in a very simplified way for the sake of illustration, the problem of recovering information about vessel features by evaluating physical indices related to flow variables is of general interest for diagnostic purposes too. For instance, fractional flow reserve is a procedure exploited in coronary catheterization to measure pressure differences across a coronary artery stenosis in order to determine the degree of stenosis.
$\unicode[STIX]{x1D6E4}_{\mathit{in}}$
: see Figure 11.2(a). For simplicity, a steady incompressible Navier–Stokes model is employed to model the blood flow, although the same approach concerning the solution of the inverse UQ problem can be applied to the case of an unsteady fluid model, as soon as a peak (or time average) pressure drop is evaluated. Although presented here in a very simplified way for the sake of illustration, the problem of recovering information about vessel features by evaluating physical indices related to flow variables is of general interest for diagnostic purposes too. For instance, fractional flow reserve is a procedure exploited in coronary catheterization to measure pressure differences across a coronary artery stenosis in order to determine the degree of stenosis.
The parameter estimation problem is first solved by minimizing a least-squares functional for different observations of the pressure drop,
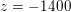 $z=-1400$
and
$z=-1400$
and
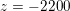 $z=-2200$
, by assuming
$z=-2200$
, by assuming
![]() $5\%$
relative additive noise in the measurements. The results of the inverse identification problem are represented in Figure 11.2(b) for 100 realizations of random noise in both cases. The recovered diameter values are shown to be quite sensitive to small noise variations. This is due to the fact that several geometric configurations – in terms of diameters
$5\%$
relative additive noise in the measurements. The results of the inverse identification problem are represented in Figure 11.2(b) for 100 realizations of random noise in both cases. The recovered diameter values are shown to be quite sensitive to small noise variations. This is due to the fact that several geometric configurations – in terms of diameters
![]() $(d_{c},d_{b})$
– may correspond to the same output observation. The backward UQ propagation problem is then solved in a Bayesian setting, characterizing the posterior PDF of
$(d_{c},d_{b})$
– may correspond to the same output observation. The backward UQ propagation problem is then solved in a Bayesian setting, characterizing the posterior PDF of
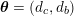 $\boldsymbol{\unicode[STIX]{x1D703}}=(d_{c},d_{b})$
starting from a Gaussian prior and assuming a Gaussian model to describe experimental noise. In particular, we can assume that the two diameters are either a priori independent (case (c), left), or correlated (case (c), right)). The two corresponding posterior distributions, obtained for the observations
$\boldsymbol{\unicode[STIX]{x1D703}}=(d_{c},d_{b})$
starting from a Gaussian prior and assuming a Gaussian model to describe experimental noise. In particular, we can assume that the two diameters are either a priori independent (case (c), left), or correlated (case (c), right)). The two corresponding posterior distributions, obtained for the observations
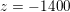 $z=-1400$
and
$z=-1400$
and
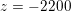 $z=-2200$
of the pressure drop, are shown in Figure 11.2(d, e).
$z=-2200$
of the pressure drop, are shown in Figure 11.2(d, e).
11.3.2 Backward uncertainty propagation in cardiac electrophysiology
We finally consider the problem of identifying the size and the position of an ischaemic region in the myocardial tissue, as a remarkable instance of a backward UQ problem dealing with cardiovascular applications. Such a problem case can be cast in the form of a joint state/parameter estimation problem, and can be tackled efficiently by an EnKF technique.
The state evolution equation is given by the (space and time discretization of the) monodomain equation for the trans-membrane potential
![]() $V_{m}$
, coupled with an Aliev–Panfilov cellular model involving a single gating variable
$V_{m}$
, coupled with an Aliev–Panfilov cellular model involving a single gating variable
![]() $w$
; the state variable is thus
$w$
; the state variable is thus
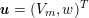 $\boldsymbol{u}=(V_{m},w)^{T}$
. Similarly to the example in Section 11.1, to represent lack of conductivity in the tissue we introduce the relative conductivity
$\boldsymbol{u}=(V_{m},w)^{T}$
. Similarly to the example in Section 11.1, to represent lack of conductivity in the tissue we introduce the relative conductivity
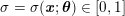 $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}(\boldsymbol{x};\boldsymbol{\unicode[STIX]{x1D703}})\in [0,1]$
;
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}(\boldsymbol{x};\boldsymbol{\unicode[STIX]{x1D703}})\in [0,1]$
;
![]() $\unicode[STIX]{x1D70E}=1$
and
$\unicode[STIX]{x1D70E}=1$
and
![]() $\unicode[STIX]{x1D70E}=0$
correspond to proper electrical conduction or total lack of conductivity, respectively.
$\unicode[STIX]{x1D70E}=0$
correspond to proper electrical conduction or total lack of conductivity, respectively.
Since the position and the extension of the ischaemic region is unknown,
![]() $\unicode[STIX]{x1D70E}(\boldsymbol{x};\boldsymbol{\unicode[STIX]{x1D703}})$
is a random field. To make its representation low-dimensional, we parametrize the field
$\unicode[STIX]{x1D70E}(\boldsymbol{x};\boldsymbol{\unicode[STIX]{x1D703}})$
is a random field. To make its representation low-dimensional, we parametrize the field
![]() $\unicode[STIX]{x1D70E}(\boldsymbol{x};\boldsymbol{\unicode[STIX]{x1D703}})$
in terms of
$\unicode[STIX]{x1D70E}(\boldsymbol{x};\boldsymbol{\unicode[STIX]{x1D703}})$
in terms of
![]() $p=20$
random inputs
$p=20$
random inputs
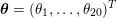 $\boldsymbol{\unicode[STIX]{x1D703}}=(\unicode[STIX]{x1D703}_{1},\ldots ,\unicode[STIX]{x1D703}_{20})^{T}$
entering into a linear combination of
$\boldsymbol{\unicode[STIX]{x1D703}}=(\unicode[STIX]{x1D703}_{1},\ldots ,\unicode[STIX]{x1D703}_{20})^{T}$
entering into a linear combination of
![]() $p=20$
radial basis functions (RBFs), around
$p=20$
radial basis functions (RBFs), around
![]() $p$
given centres
$p$
given centres
![]() $\{\boldsymbol{x}_{i}\}_{i=1}^{20}$
,
$\{\boldsymbol{x}_{i}\}_{i=1}^{20}$
,
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}(\boldsymbol{x};\boldsymbol{\unicode[STIX]{x1D703}})=\frac{1}{\unicode[STIX]{x1D708}(\boldsymbol{x})}\mathop{\sum }_{i=1}^{p}\unicode[STIX]{x1D703}_{i}\exp \biggl(-\frac{\Vert \boldsymbol{x}-\boldsymbol{x}_{i}\Vert ^{2}}{\unicode[STIX]{x1D706}^{2}}\biggr),\quad \unicode[STIX]{x1D708}(\boldsymbol{x})=\mathop{\sum }_{i=1}^{p}\exp \biggl(-\frac{\Vert \boldsymbol{x}-\boldsymbol{x}_{i}\Vert ^{2}}{\unicode[STIX]{x1D706}^{2}}\biggr),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}(\boldsymbol{x};\boldsymbol{\unicode[STIX]{x1D703}})=\frac{1}{\unicode[STIX]{x1D708}(\boldsymbol{x})}\mathop{\sum }_{i=1}^{p}\unicode[STIX]{x1D703}_{i}\exp \biggl(-\frac{\Vert \boldsymbol{x}-\boldsymbol{x}_{i}\Vert ^{2}}{\unicode[STIX]{x1D706}^{2}}\biggr),\quad \unicode[STIX]{x1D708}(\boldsymbol{x})=\mathop{\sum }_{i=1}^{p}\exp \biggl(-\frac{\Vert \boldsymbol{x}-\boldsymbol{x}_{i}\Vert ^{2}}{\unicode[STIX]{x1D706}^{2}}\biggr),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D708}(\boldsymbol{x})$
is a normalization factor so that
$\unicode[STIX]{x1D708}(\boldsymbol{x})$
is a normalization factor so that
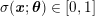 $\unicode[STIX]{x1D70E}(\boldsymbol{x};\boldsymbol{\unicode[STIX]{x1D703}})\in [0,1]$
. We consider a patient-specific left-ventricle geometry, and assume that a dataset
$\unicode[STIX]{x1D70E}(\boldsymbol{x};\boldsymbol{\unicode[STIX]{x1D703}})\in [0,1]$
. We consider a patient-specific left-ventricle geometry, and assume that a dataset
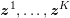 $\boldsymbol{z}^{1},\ldots ,\boldsymbol{z}^{K}$
is acquired sequentially over a time interval. In particular, at each time
$\boldsymbol{z}^{1},\ldots ,\boldsymbol{z}^{K}$
is acquired sequentially over a time interval. In particular, at each time
![]() $\unicode[STIX]{x1D70F}^{k}$
,
$\unicode[STIX]{x1D70F}^{k}$
,
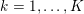 $k=1,\ldots ,K$
, data are given by the trans-membrane potential values computed at a set of nine points located on the endocardium, contaminated by Gaussian noise with zero mean and known covariance, to simulate the effect of experimental noise while evaluating the so-called simultaneous endocardial mapping in the human left ventricle; these invasive measurements are usually obtained using a non-contact catheter (see e.g. Schilling, Peters and Davies Reference Schilling, Peters and Davies1998, Álvarez et al. Reference Álvarez, Alonso-Atienza, Rojo-Álvarez, Garcia-Alberola and Moscoso2012). For the sake of the computational experiment, we assume that the data
$k=1,\ldots ,K$
, data are given by the trans-membrane potential values computed at a set of nine points located on the endocardium, contaminated by Gaussian noise with zero mean and known covariance, to simulate the effect of experimental noise while evaluating the so-called simultaneous endocardial mapping in the human left ventricle; these invasive measurements are usually obtained using a non-contact catheter (see e.g. Schilling, Peters and Davies Reference Schilling, Peters and Davies1998, Álvarez et al. Reference Álvarez, Alonso-Atienza, Rojo-Álvarez, Garcia-Alberola and Moscoso2012). For the sake of the computational experiment, we assume that the data
![]() $\boldsymbol{z}^{k}$
,
$\boldsymbol{z}^{k}$
,
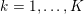 $k=1,\ldots ,K$
, are generated by the monodomain model with relative conductivity
$k=1,\ldots ,K$
, are generated by the monodomain model with relative conductivity
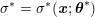 $\unicode[STIX]{x1D70E}^{\ast }=\unicode[STIX]{x1D70E}^{\ast }(\boldsymbol{x};\boldsymbol{\unicode[STIX]{x1D703}}^{\ast })$
for a particular choice
$\unicode[STIX]{x1D70E}^{\ast }=\unicode[STIX]{x1D70E}^{\ast }(\boldsymbol{x};\boldsymbol{\unicode[STIX]{x1D703}}^{\ast })$
for a particular choice
![]() $\boldsymbol{\unicode[STIX]{x1D703}}=\boldsymbol{\unicode[STIX]{x1D703}}^{\ast }$
of the input vector, that is,
$\boldsymbol{\unicode[STIX]{x1D703}}=\boldsymbol{\unicode[STIX]{x1D703}}^{\ast }$
of the input vector, that is,
 $$\begin{eqnarray}\boldsymbol{z}^{k}=\boldsymbol{h}(\boldsymbol{u}(\boldsymbol{\unicode[STIX]{x1D703}}^{\ast }))+\boldsymbol{\unicode[STIX]{x1D702}}^{k},\quad \boldsymbol{\unicode[STIX]{x1D702}}^{k}\sim N(\mathbf{0},R_{k}).\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{z}^{k}=\boldsymbol{h}(\boldsymbol{u}(\boldsymbol{\unicode[STIX]{x1D703}}^{\ast }))+\boldsymbol{\unicode[STIX]{x1D702}}^{k},\quad \boldsymbol{\unicode[STIX]{x1D702}}^{k}\sim N(\mathbf{0},R_{k}).\end{eqnarray}$$
The goal is thus to recover the (posterior) PDF of
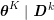 $\boldsymbol{\unicode[STIX]{x1D703}}^{K}\mid \boldsymbol{D}^{k}$
given the observations
$\boldsymbol{\unicode[STIX]{x1D703}}^{K}\mid \boldsymbol{D}^{k}$
given the observations
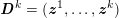 $\boldsymbol{D}^{k}=(\boldsymbol{z}^{1},\ldots ,\boldsymbol{z}^{k})$
, evaluate the conditional mean
$\boldsymbol{D}^{k}=(\boldsymbol{z}^{1},\ldots ,\boldsymbol{z}^{k})$
, evaluate the conditional mean
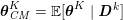 $\boldsymbol{\unicode[STIX]{x1D703}}_{\mathit{CM}}^{K}=\mathbb{E}[\boldsymbol{\unicode[STIX]{x1D703}}^{K}\mid \boldsymbol{D}^{k}]$
, and finally estimate the conductivity field as
$\boldsymbol{\unicode[STIX]{x1D703}}_{\mathit{CM}}^{K}=\mathbb{E}[\boldsymbol{\unicode[STIX]{x1D703}}^{K}\mid \boldsymbol{D}^{k}]$
, and finally estimate the conductivity field as
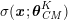 $\unicode[STIX]{x1D70E}(\boldsymbol{x};\boldsymbol{\unicode[STIX]{x1D703}}_{\mathit{CM}}^{K})$
.
$\unicode[STIX]{x1D70E}(\boldsymbol{x};\boldsymbol{\unicode[STIX]{x1D703}}_{\mathit{CM}}^{K})$
.
Starting from a prior distribution for the input vector
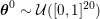 $\boldsymbol{\unicode[STIX]{x1D703}}^{0}\sim {\mathcal{U}}([0,1]^{20})$
, reflecting the lack of information about the possible presence and position of the ischaemic region, we rely on the EnKF to produce sequentially an ensemble
$\boldsymbol{\unicode[STIX]{x1D703}}^{0}\sim {\mathcal{U}}([0,1]^{20})$
, reflecting the lack of information about the possible presence and position of the ischaemic region, we rely on the EnKF to produce sequentially an ensemble
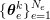 $\{\boldsymbol{\unicode[STIX]{x1D703}}_{e}^{k}\}_{e=1}^{N_{e}}$
of
$\{\boldsymbol{\unicode[STIX]{x1D703}}_{e}^{k}\}_{e=1}^{N_{e}}$
of
![]() $N_{e}$
particles distributed according to the conditional distribution
$N_{e}$
particles distributed according to the conditional distribution
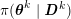 $\unicode[STIX]{x1D70B}(\boldsymbol{\unicode[STIX]{x1D703}}^{k}\mid \boldsymbol{D}^{k})$
, and the associated ensemble of
$\unicode[STIX]{x1D70B}(\boldsymbol{\unicode[STIX]{x1D703}}^{k}\mid \boldsymbol{D}^{k})$
, and the associated ensemble of
![]() $N_{e}$
states
$N_{e}$
states
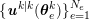 $\{\boldsymbol{u}^{k|k}(\boldsymbol{\unicode[STIX]{x1D703}}_{e}^{k})\}_{e=1}^{N_{e}}$
. Hence, starting from the initial ensemble
$\{\boldsymbol{u}^{k|k}(\boldsymbol{\unicode[STIX]{x1D703}}_{e}^{k})\}_{e=1}^{N_{e}}$
. Hence, starting from the initial ensemble
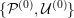 $\{{\mathcal{P}}^{(0)},{\mathcal{U}}^{(0)}\}$
sampled from the prior distribution, the prediction-analysis procedure of the EnKF is given by the following two-stage recursion.
$\{{\mathcal{P}}^{(0)},{\mathcal{U}}^{(0)}\}$
sampled from the prior distribution, the prediction-analysis procedure of the EnKF is given by the following two-stage recursion.

Figure 11.3. (a) 5% quantile, mean and 95% quantile of the uniform prior distribution of
![]() $\boldsymbol{\unicode[STIX]{x1D703}}^{0}$
. (b) Identification of
$\boldsymbol{\unicode[STIX]{x1D703}}^{0}$
. (b) Identification of
![]() $p=20$
parameters via the EnKF algorithm. Reference values
$p=20$
parameters via the EnKF algorithm. Reference values
![]() $\unicode[STIX]{x1D703}_{i}^{\ast }$
,
$\unicode[STIX]{x1D703}_{i}^{\ast }$
,
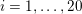 $i=1,\ldots ,20$
, estimates
$i=1,\ldots ,20$
, estimates
![]() $(\bar{\unicode[STIX]{x1D703}}_{e}^{k})_{i}$
and confidence intervals are reported in dotted red, solid blue and dotted blue lines, respectively. (c) 5% quantile, conditional mean and 95% quantile of the posterior distribution of
$(\bar{\unicode[STIX]{x1D703}}_{e}^{k})_{i}$
and confidence intervals are reported in dotted red, solid blue and dotted blue lines, respectively. (c) 5% quantile, conditional mean and 95% quantile of the posterior distribution of
![]() $\boldsymbol{\unicode[STIX]{x1D703}}^{K}$
. Numerical results were obtained using the finite element library redbKIT v2.1 (github.com/redbKIT/redbKIT/releases).
$\boldsymbol{\unicode[STIX]{x1D703}}^{K}$
. Numerical results were obtained using the finite element library redbKIT v2.1 (github.com/redbKIT/redbKIT/releases).
-
(1) At each prediction step, compute the solution
 $\boldsymbol{u}^{k|k-1}(\boldsymbol{\unicode[STIX]{x1D703}}_{e}^{k-1})$
of the state system over
$\boldsymbol{u}^{k|k-1}(\boldsymbol{\unicode[STIX]{x1D703}}_{e}^{k-1})$
of the state system over
 $[\unicode[STIX]{x1D70F}^{k-1},\unicode[STIX]{x1D70F}^{k})$
with initial datum
$[\unicode[STIX]{x1D70F}^{k-1},\unicode[STIX]{x1D70F}^{k})$
with initial datum
 $\boldsymbol{u}^{k|k-1}(\boldsymbol{\unicode[STIX]{x1D703}}_{e}^{k-1})$
.
$\boldsymbol{u}^{k|k-1}(\boldsymbol{\unicode[STIX]{x1D703}}_{e}^{k-1})$
. -
(2) At each correction step, the observation
 $\boldsymbol{z}^{k}$
is replicated
$\boldsymbol{z}^{k}$
is replicated
 $N_{e}$
times, obtaining Then, compute the sample means
$N_{e}$
times, obtaining Then, compute the sample means $$\begin{eqnarray}\boldsymbol{d}_{e}^{k}=\boldsymbol{z}^{k}+\boldsymbol{\unicode[STIX]{x1D702}}_{e}^{k},\quad \boldsymbol{\unicode[STIX]{x1D702}}_{e}^{k}\sim N(\mathbf{0},R_{k}).\end{eqnarray}$$
(11.9)and the sample covariances
$$\begin{eqnarray}\boldsymbol{d}_{e}^{k}=\boldsymbol{z}^{k}+\boldsymbol{\unicode[STIX]{x1D702}}_{e}^{k},\quad \boldsymbol{\unicode[STIX]{x1D702}}_{e}^{k}\sim N(\mathbf{0},R_{k}).\end{eqnarray}$$
(11.9)and the sample covariances $$\begin{eqnarray}\displaystyle \overline{\boldsymbol{u}}^{k|k-1} & = & \displaystyle \frac{1}{N_{e}}\mathop{\sum }_{e=1}^{N_{e}}\boldsymbol{u}^{k|k-1}(\boldsymbol{\unicode[STIX]{x1D703}}_{e}^{k-1}),\nonumber\\ \displaystyle \overline{\boldsymbol{s}}_{e}^{k|k-1} & = & \displaystyle \frac{1}{N_{e}}\mathop{\sum }_{e=1}^{N_{e}}\boldsymbol{h}(\boldsymbol{u}^{k|k-1}(\boldsymbol{\unicode[STIX]{x1D703}}_{e}^{k-1})),\nonumber\\ \displaystyle \overline{\boldsymbol{\unicode[STIX]{x1D703}}}_{e}^{k-1} & = & \displaystyle \frac{1}{N_{e}}\mathop{\sum }_{e=1}^{N_{e}}\boldsymbol{\unicode[STIX]{x1D703}}_{e}^{k-1},\end{eqnarray}$$
(11.10)
$$\begin{eqnarray}\displaystyle \overline{\boldsymbol{u}}^{k|k-1} & = & \displaystyle \frac{1}{N_{e}}\mathop{\sum }_{e=1}^{N_{e}}\boldsymbol{u}^{k|k-1}(\boldsymbol{\unicode[STIX]{x1D703}}_{e}^{k-1}),\nonumber\\ \displaystyle \overline{\boldsymbol{s}}_{e}^{k|k-1} & = & \displaystyle \frac{1}{N_{e}}\mathop{\sum }_{e=1}^{N_{e}}\boldsymbol{h}(\boldsymbol{u}^{k|k-1}(\boldsymbol{\unicode[STIX]{x1D703}}_{e}^{k-1})),\nonumber\\ \displaystyle \overline{\boldsymbol{\unicode[STIX]{x1D703}}}_{e}^{k-1} & = & \displaystyle \frac{1}{N_{e}}\mathop{\sum }_{e=1}^{N_{e}}\boldsymbol{\unicode[STIX]{x1D703}}_{e}^{k-1},\end{eqnarray}$$
(11.10) $$\begin{eqnarray}\displaystyle \mathbf{C}_{ss}^{k} & = & \displaystyle \frac{1}{N_{e}-1}\mathop{\sum }_{e=1}^{N_{e}}\boldsymbol{v}_{e}\boldsymbol{v}_{e}^{T}\in \mathbb{R}^{n_{z}\times n_{z}},\end{eqnarray}$$
(11.11)
$$\begin{eqnarray}\displaystyle \mathbf{C}_{ss}^{k} & = & \displaystyle \frac{1}{N_{e}-1}\mathop{\sum }_{e=1}^{N_{e}}\boldsymbol{v}_{e}\boldsymbol{v}_{e}^{T}\in \mathbb{R}^{n_{z}\times n_{z}},\end{eqnarray}$$
(11.11) $$\begin{eqnarray}\displaystyle \mathbf{C}_{\unicode[STIX]{x1D703}s}^{k} & = & \displaystyle \frac{1}{N_{e}-1}\mathop{\sum }_{e=1}^{N_{e}}(\boldsymbol{\unicode[STIX]{x1D703}}_{e}^{k-1}-\overline{\boldsymbol{\unicode[STIX]{x1D703}}}_{e}^{k-1})\boldsymbol{v}_{e}^{T}\in \mathbb{R}^{p\times n_{z}},\end{eqnarray}$$
(11.12)where
$$\begin{eqnarray}\displaystyle \mathbf{C}_{\unicode[STIX]{x1D703}s}^{k} & = & \displaystyle \frac{1}{N_{e}-1}\mathop{\sum }_{e=1}^{N_{e}}(\boldsymbol{\unicode[STIX]{x1D703}}_{e}^{k-1}-\overline{\boldsymbol{\unicode[STIX]{x1D703}}}_{e}^{k-1})\boldsymbol{v}_{e}^{T}\in \mathbb{R}^{p\times n_{z}},\end{eqnarray}$$
(11.12)where $$\begin{eqnarray}\displaystyle \mathbf{C}_{us}^{k} & = & \displaystyle \frac{1}{N_{e}-1}\mathop{\sum }_{e=1}^{N_{e}}(\boldsymbol{u}^{k|k-1}(\boldsymbol{\unicode[STIX]{x1D703}}_{e}^{k-1})-\overline{\boldsymbol{u}}^{k|k-1})\boldsymbol{v}_{e}^{T}\in \mathbb{R}^{n_{x}\times n_{z}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbf{C}_{us}^{k} & = & \displaystyle \frac{1}{N_{e}-1}\mathop{\sum }_{e=1}^{N_{e}}(\boldsymbol{u}^{k|k-1}(\boldsymbol{\unicode[STIX]{x1D703}}_{e}^{k-1})-\overline{\boldsymbol{u}}^{k|k-1})\boldsymbol{v}_{e}^{T}\in \mathbb{R}^{n_{x}\times n_{z}},\end{eqnarray}$$
 $\boldsymbol{v}_{e}=\boldsymbol{h}(\boldsymbol{u}^{k|k-1}(\boldsymbol{\unicode[STIX]{x1D703}}_{e}^{k-1}))$
. Finally, the state/parameter ensembles are updated via the Kalman formula
(11.13)for
$\boldsymbol{v}_{e}=\boldsymbol{h}(\boldsymbol{u}^{k|k-1}(\boldsymbol{\unicode[STIX]{x1D703}}_{e}^{k-1}))$
. Finally, the state/parameter ensembles are updated via the Kalman formula
(11.13)for $$\begin{eqnarray}\left[\begin{array}{@{}c@{}}\boldsymbol{\unicode[STIX]{x1D703}}_{e}^{k}\\ \boldsymbol{u}^{k|k}(\boldsymbol{\unicode[STIX]{x1D703}}_{e}^{k})\end{array}\right]=\left[\begin{array}{@{}c@{}}\boldsymbol{\unicode[STIX]{x1D703}}_{e}^{k-1}\\ \boldsymbol{u}^{k}(\boldsymbol{\unicode[STIX]{x1D703}}_{e}^{k-1})\end{array}\right]+\left[\begin{array}{@{}c@{}}\mathbf{C}_{\unicode[STIX]{x1D703}z}^{k}\\ \mathbf{C}_{uz}^{k}\end{array}\right](R_{k}+\mathbf{C}_{zz}^{k})^{-1}(\boldsymbol{d}_{e}^{k}-\boldsymbol{h}(\boldsymbol{u}^{k|k-1}(\boldsymbol{\unicode[STIX]{x1D703}}_{e}^{k-1}))),\end{eqnarray}$$
$$\begin{eqnarray}\left[\begin{array}{@{}c@{}}\boldsymbol{\unicode[STIX]{x1D703}}_{e}^{k}\\ \boldsymbol{u}^{k|k}(\boldsymbol{\unicode[STIX]{x1D703}}_{e}^{k})\end{array}\right]=\left[\begin{array}{@{}c@{}}\boldsymbol{\unicode[STIX]{x1D703}}_{e}^{k-1}\\ \boldsymbol{u}^{k}(\boldsymbol{\unicode[STIX]{x1D703}}_{e}^{k-1})\end{array}\right]+\left[\begin{array}{@{}c@{}}\mathbf{C}_{\unicode[STIX]{x1D703}z}^{k}\\ \mathbf{C}_{uz}^{k}\end{array}\right](R_{k}+\mathbf{C}_{zz}^{k})^{-1}(\boldsymbol{d}_{e}^{k}-\boldsymbol{h}(\boldsymbol{u}^{k|k-1}(\boldsymbol{\unicode[STIX]{x1D703}}_{e}^{k-1}))),\end{eqnarray}$$
 $e=1,\ldots ,N_{e}$
.
$e=1,\ldots ,N_{e}$
.
The numerical results obtained by this procedure are shown in Figure 11.3. The data were generated by the monodomain model with the relative conductivity field
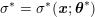 $\unicode[STIX]{x1D70E}^{\ast }=\unicode[STIX]{x1D70E}^{\ast }(\boldsymbol{x};\boldsymbol{\unicode[STIX]{x1D703}}^{\ast })$
shown in Figure 11.3(a); a uniform prior distribution
$\unicode[STIX]{x1D70E}^{\ast }=\unicode[STIX]{x1D70E}^{\ast }(\boldsymbol{x};\boldsymbol{\unicode[STIX]{x1D703}}^{\ast })$
shown in Figure 11.3(a); a uniform prior distribution
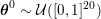 $\boldsymbol{\unicode[STIX]{x1D703}}^{0}\sim {\mathcal{U}}([0,1]^{20})$
is assumed. After executing the EnKF algorithm, we obtain the posterior distribution whose mean and
$\boldsymbol{\unicode[STIX]{x1D703}}^{0}\sim {\mathcal{U}}([0,1]^{20})$
is assumed. After executing the EnKF algorithm, we obtain the posterior distribution whose mean and
![]() $5\%$
,
$5\%$
,
![]() $95\%$
quantiles are shown in Figure 11.3(c). The uncertainty in the input parameters is greatly reduced, while the conditional mean of the posterior distribution correctly approximates the realization of the random field reported on the left, by which data exploited for the sake of parameter estimation have been generated.
$95\%$
quantiles are shown in Figure 11.3(c). The uncertainty in the input parameters is greatly reduced, while the conditional mean of the posterior distribution correctly approximates the realization of the random field reported on the left, by which data exploited for the sake of parameter estimation have been generated.
12 Reduced-order modelling
As seen in Sections 9–11, several numerical strategies used to tackle PDE-constrained optimization, parameter estimation and uncertainty quantification problems arising in cardiovascular modelling involve the approximation of PDE systems for several input parameter values. On the other hand, the repeated evaluation of input/output maps to characterize different scenarios requires many queries to numerical models too. Further, if quantitative outputs are meant to support clinicians and medical doctors in their decisions, each new numerical simulation should be carried out very rapidly (order of minutes, say) on deployed platforms rather than on huge parallel hardware architectures, possibly requiring limited data storage and memory capacity. Meeting all these requirements is a challenging task, with the result that traditional high-fidelity, or full-order, techniques (e.g. the finite element method) are ill-suited, despite the constant growth of computer resources available.
Reduced-order models (ROMs) are emerging methodologies aimed at reducing the computational complexity and costs entailed by the repeated solution of PDE problems (Antoulas Reference Antoulas2005, Benner, Gugercin and Willcox Reference Benner, Gugercin and Willcox2015, Quarteroni and Rozza Reference Quarteroni and Rozza2014). In the case of parametrized PDEs (i.e. PDEs depending on a vector of parameters
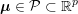 $\boldsymbol{\unicode[STIX]{x1D707}}\in {\mathcal{P}}\subset \mathbb{R}^{p}$
), the reduced basis (RB) method is a remarkable example of a ROM that enables dramatic reduction of the dimension of the discrete problems arising from numerical approximation – from millions to hundreds, or thousands at most, of variables.
$\boldsymbol{\unicode[STIX]{x1D707}}\in {\mathcal{P}}\subset \mathbb{R}^{p}$
), the reduced basis (RB) method is a remarkable example of a ROM that enables dramatic reduction of the dimension of the discrete problems arising from numerical approximation – from millions to hundreds, or thousands at most, of variables.
Here,
![]() $\mathbf{y}(t;\boldsymbol{\unicode[STIX]{x1D707}})$
denote the solution of a time-dependent non-linear problem (
$\mathbf{y}(t;\boldsymbol{\unicode[STIX]{x1D707}})$
denote the solution of a time-dependent non-linear problem (
 $\boldsymbol{\unicode[STIX]{x1D707}}\in {\mathcal{P}}\subset \mathbb{R}^{p}$
denotes a set of input parameters) of the form
$\boldsymbol{\unicode[STIX]{x1D707}}\in {\mathcal{P}}\subset \mathbb{R}^{p}$
denotes a set of input parameters) of the form
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}rcl@{}}M(\boldsymbol{\unicode[STIX]{x1D707}})\frac{\text{d}\mathbf{y}(t;\boldsymbol{\unicode[STIX]{x1D707}})}{\text{d}t}+A(\boldsymbol{\unicode[STIX]{x1D707}})\mathbf{y}(t;\boldsymbol{\unicode[STIX]{x1D707}})+F(\mathbf{y}(t;\boldsymbol{\unicode[STIX]{x1D707}})) & = & \mathbf{f}(t;\boldsymbol{\unicode[STIX]{x1D707}}),\quad t\in (0,T],\\ \mathbf{y}(0;\boldsymbol{\unicode[STIX]{x1D707}}) & = & \mathbf{y}_{0}(\boldsymbol{\unicode[STIX]{x1D707}}),\end{array} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}rcl@{}}M(\boldsymbol{\unicode[STIX]{x1D707}})\frac{\text{d}\mathbf{y}(t;\boldsymbol{\unicode[STIX]{x1D707}})}{\text{d}t}+A(\boldsymbol{\unicode[STIX]{x1D707}})\mathbf{y}(t;\boldsymbol{\unicode[STIX]{x1D707}})+F(\mathbf{y}(t;\boldsymbol{\unicode[STIX]{x1D707}})) & = & \mathbf{f}(t;\boldsymbol{\unicode[STIX]{x1D707}}),\quad t\in (0,T],\\ \mathbf{y}(0;\boldsymbol{\unicode[STIX]{x1D707}}) & = & \mathbf{y}_{0}(\boldsymbol{\unicode[STIX]{x1D707}}),\end{array} & & \displaystyle\end{eqnarray}$$
stemming from the (e.g. finite element) discretization of a parametrized PDE, where
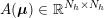 $A(\boldsymbol{\unicode[STIX]{x1D707}})\in \mathbb{R}^{N_{h}\times N_{h}}$
,
$A(\boldsymbol{\unicode[STIX]{x1D707}})\in \mathbb{R}^{N_{h}\times N_{h}}$
,
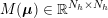 $M(\boldsymbol{\unicode[STIX]{x1D707}})\in \mathbb{R}^{N_{h}\times N_{h}}$
and
$M(\boldsymbol{\unicode[STIX]{x1D707}})\in \mathbb{R}^{N_{h}\times N_{h}}$
and
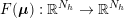 $F(\boldsymbol{\unicode[STIX]{x1D707}}):\mathbb{R}^{N_{h}}\rightarrow \mathbb{R}^{N_{h}}$
are three operators corresponding to the linear, mass and non-linear terms of the PDE.
$F(\boldsymbol{\unicode[STIX]{x1D707}}):\mathbb{R}^{N_{h}}\rightarrow \mathbb{R}^{N_{h}}$
are three operators corresponding to the linear, mass and non-linear terms of the PDE.
The dimensional reduction is made possible by exploiting the parametric dependence of the solution manifold, that is, the set
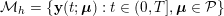 ${\mathcal{M}}_{h}=\{\mathbf{y}(t;\boldsymbol{\unicode[STIX]{x1D707}}):t\in (0,T],\boldsymbol{\unicode[STIX]{x1D707}}\in {\mathcal{P}}\}$
, thanks to the evaluation of a database of solutions, or snapshots, for selected parameter values, and to a (Petrov–) Galerkin projection onto the RB space spanned by a set of RB functions. In the case of a stationary problem, these latter are the snapshots themselves if a greedy algorithm is used, or the first singular vectors of the snapshot matrix if proper orthogonal decomposition (POD) is used: see e.g. Quarteroni, Manzoni and Negri (Reference Quarteroni, Manzoni and Negri2016), Hesthaven, Rozza and Stamm (Reference Hesthaven, Rozza and Stamm2016) and Cohen and DeVore (Reference Cohen and Devore2015). For time-dependent problems, the parameter space can still be sampled by relying on one of the two techniques mentioned, whereas POD is usually exploited to reduce trajectories of the system over the time interval.
${\mathcal{M}}_{h}=\{\mathbf{y}(t;\boldsymbol{\unicode[STIX]{x1D707}}):t\in (0,T],\boldsymbol{\unicode[STIX]{x1D707}}\in {\mathcal{P}}\}$
, thanks to the evaluation of a database of solutions, or snapshots, for selected parameter values, and to a (Petrov–) Galerkin projection onto the RB space spanned by a set of RB functions. In the case of a stationary problem, these latter are the snapshots themselves if a greedy algorithm is used, or the first singular vectors of the snapshot matrix if proper orthogonal decomposition (POD) is used: see e.g. Quarteroni, Manzoni and Negri (Reference Quarteroni, Manzoni and Negri2016), Hesthaven, Rozza and Stamm (Reference Hesthaven, Rozza and Stamm2016) and Cohen and DeVore (Reference Cohen and Devore2015). For time-dependent problems, the parameter space can still be sampled by relying on one of the two techniques mentioned, whereas POD is usually exploited to reduce trajectories of the system over the time interval.
Hence, the RB method seeks an approximation
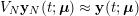 $V_{N}\mathbf{y}_{N}(t;\boldsymbol{\unicode[STIX]{x1D707}})\approx \mathbf{y}(t;\boldsymbol{\unicode[STIX]{x1D707}})$
to the solution of (12.1), where
$V_{N}\mathbf{y}_{N}(t;\boldsymbol{\unicode[STIX]{x1D707}})\approx \mathbf{y}(t;\boldsymbol{\unicode[STIX]{x1D707}})$
to the solution of (12.1), where
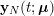 $\mathbf{y}_{N}(t;\boldsymbol{\unicode[STIX]{x1D707}})$
is the reduced state vector and
$\mathbf{y}_{N}(t;\boldsymbol{\unicode[STIX]{x1D707}})$
is the reduced state vector and
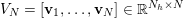 $V_{N}=[\mathbf{v}_{1},\ldots ,\mathbf{v}_{N}]\in \mathbb{R}^{N_{h}\times N}$
is a matrix stacking the RB functions by columns. One possible RB approximation of (12.1) might be
$V_{N}=[\mathbf{v}_{1},\ldots ,\mathbf{v}_{N}]\in \mathbb{R}^{N_{h}\times N}$
is a matrix stacking the RB functions by columns. One possible RB approximation of (12.1) might be
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}rcl@{}}\displaystyle M_{N}(\boldsymbol{\unicode[STIX]{x1D707}})\frac{\text{d}\mathbf{y}_{N}(t;\boldsymbol{\unicode[STIX]{x1D707}})}{\text{d}t}+A_{N}(\boldsymbol{\unicode[STIX]{x1D707}})\mathbf{y}_{N}(t;\boldsymbol{\unicode[STIX]{x1D707}}) & & \\ \displaystyle +V_{N}^{T}\mathbf{F}(V_{N}\mathbf{y}_{N}(t;\boldsymbol{\unicode[STIX]{x1D707}})) & = & \mathbf{f}_{N}(t;\boldsymbol{\unicode[STIX]{x1D707}}),\quad t\in (0,T]\\ \displaystyle \mathbf{y}_{N}(0;\boldsymbol{\unicode[STIX]{x1D707}}) & = & \mathbf{y}_{N,0}(\boldsymbol{\unicode[STIX]{x1D707}}),\end{array} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}rcl@{}}\displaystyle M_{N}(\boldsymbol{\unicode[STIX]{x1D707}})\frac{\text{d}\mathbf{y}_{N}(t;\boldsymbol{\unicode[STIX]{x1D707}})}{\text{d}t}+A_{N}(\boldsymbol{\unicode[STIX]{x1D707}})\mathbf{y}_{N}(t;\boldsymbol{\unicode[STIX]{x1D707}}) & & \\ \displaystyle +V_{N}^{T}\mathbf{F}(V_{N}\mathbf{y}_{N}(t;\boldsymbol{\unicode[STIX]{x1D707}})) & = & \mathbf{f}_{N}(t;\boldsymbol{\unicode[STIX]{x1D707}}),\quad t\in (0,T]\\ \displaystyle \mathbf{y}_{N}(0;\boldsymbol{\unicode[STIX]{x1D707}}) & = & \mathbf{y}_{N,0}(\boldsymbol{\unicode[STIX]{x1D707}}),\end{array} & & \displaystyle\end{eqnarray}$$
where
 $$\begin{eqnarray}A_{N}(\boldsymbol{\unicode[STIX]{x1D707}})=V_{N}^{T}A(\boldsymbol{\unicode[STIX]{x1D707}})V_{N},\quad M_{N}(\boldsymbol{\unicode[STIX]{x1D707}})=V_{N}^{T}M(\boldsymbol{\unicode[STIX]{x1D707}})V_{N},\quad \mathbf{f}_{N}(t;\boldsymbol{\unicode[STIX]{x1D707}})=V_{N}^{T}\mathbf{f}(t;\boldsymbol{\unicode[STIX]{x1D707}}).\end{eqnarray}$$
$$\begin{eqnarray}A_{N}(\boldsymbol{\unicode[STIX]{x1D707}})=V_{N}^{T}A(\boldsymbol{\unicode[STIX]{x1D707}})V_{N},\quad M_{N}(\boldsymbol{\unicode[STIX]{x1D707}})=V_{N}^{T}M(\boldsymbol{\unicode[STIX]{x1D707}})V_{N},\quad \mathbf{f}_{N}(t;\boldsymbol{\unicode[STIX]{x1D707}})=V_{N}^{T}\mathbf{f}(t;\boldsymbol{\unicode[STIX]{x1D707}}).\end{eqnarray}$$
The arrays appearing in (12.2) can be efficiently assembled in a rapid online phase by combining parameter-independent quantities stored during a more expensive offline phase. Suitable hyper-reduction techniques are instead required to manage non-linear terms, in order to make their assembly independent of the dimension
![]() $N_{h}$
of the high-fidelity problem.
$N_{h}$
of the high-fidelity problem.
We emphasize that a RB method requires the solution of some full-order – and therefore very expensive – discrete equations. The key idea is that these demanding calculations can be done offline, before the optimization with respect to the control parameters, or the parameter estimation, is attempted. In fact, the cost of each optimization step performed online is much smaller than that involving the full-order state approximation; similarly, computing the evolution of a particle set in the ensemble Kalman filter algorithm by querying the ROM can thus be performed in a substantially inexpensive way.
Describing the mathematical principles and numerical algorithms underlying the RB method would take us a long way; interested readers can find a detailed presentation in Quarteroni et al. (Reference Quarteroni, Manzoni and Negri2016), for example. We limit ourselves to citing some notable applications of the RB method to problems of interest in cardiovascular modelling (this list is of course incomplete). Parametrized blood flows in idealized cardiovascular geometries have been considered by Lassila, Quarteroni and Rozza (Reference Lassila, Quarteroni and Rozza2012), Manzoni, Quarteroni and Rozza (Reference Manzoni, Quarteroni and Rozza2012a ), Ballarin et al. (Reference Ballarin, Faggiano, Ippolito, Manzoni, Quarteroni, Rozza and Scrofani2016), Ballarin et al. (Reference Ballarin, Faggiano, Manzoni, Quarteroni, Rozza, Ippolito, Antona and Scrofani2017), Colciago et al. (Reference Colciago, Deparis and Quarteroni2014) and Negri (Reference Negri2016), taking into account more complex (and computationally challenging) patient-specific configurations; in all these cases, solutions of Navier–Stokes equations are computed with respect to inflow and/or geometric parameters. Applications to PDE-constrained optimization problems arising in the context of optimal design of prosthetic devices can be found, for example, in Manzoni et al. (Reference Manzoni, Quarteroni and Rozza2012b ) and Lassila et al. (Reference Lassila, Manzoni, Quarteroni and Rozza2013a ). A reduced-order model based on POD is proposed for the bidomain equations of cardiac electrophysiology in Boulakia, Schenone and Gerbeau (Reference Boulakia, Schenone and Gerbeau2012), yielding the efficient approximation of a restitution curve and the estimation of ionic parameters and infarction locations from synthetic electrocardiograms with an evolutionary algorithm. More recently, Gerbeau, Lombardi and Schenone (Reference Gerbeau, Lombardi and Schenone2015) have proposed alternative options in this respect. Applications of POD to parameter estimation problems with sequential filtering techniques can be found in Chapelle et al. (Reference Chapelle, Gariah, Moireau and Sainte-Marie2013b ), and an application of the RB method to the computational speed-up of Bayesian inverse problems related to blood flows modelling has been reported by Lassila et al. (Reference Lassila, Manzoni, Quarteroni and Rozza2013b ) and Manzoni et al. (Reference Manzoni, Lassila, Quarteroni, Rozza, Bock, Hoang, Rannacher and Schlöder2014).
We emphasize that while physical coefficients, boundary and/or initial conditions, as well as source terms, can usually be described in terms of input parameters in a straightforward way, the task of dealing with geometries of varying shape is much more involved. In this latter case, additional techniques providing flexible descriptions of complex shapes are required, possibly involving few parameters. Notable examples are given by volume-based representations, which operate on a control volume and define parametric maps by introducing a set of control points over the control volume; control point displacements, actually inducing a shape deformation, can thus be treated as input parameters. Within this class, free-form deformation techniques and interpolants constructed over a family of radial basis functions have been successfully employed; for further details see Manzoni et al. Reference Manzoni, Quarteroni and Rozza2012a , Reference Manzoni, Quarteroni and Rozza2012b and Ballarin et al. (Reference Ballarin, Faggiano, Ippolito, Manzoni, Quarteroni, Rozza and Scrofani2016). We also point out that the need to derive flexible and low-dimensional parametrizations is not confined to the realm of RB methods for parametrized PDEs. Indeed, it also arises when dealing with random inputs or fields; in this latter case, input uncertainties are usually parametrized with respect to a finite number of random variables, corresponding to the retained terms after truncating Karhunen–Loève or polynomial chaos expansions.
The analysis, development and application of reduced-order modelling techniques is a very active field in the numerical approximation of PDEs. Without any doubt, cardiovascular applications are one of the most relevant testing environments.
Disclaimers
Despite being 590 pages long,Footnote 6 several topics related to the cardiovascular system have not been addressed in this review paper. Among others, we mention the venous system (essential if one wants to consider a closed-loop model of the cardiovascular system, and playing a crucial role in some specific pathologies: see e.g. Toro Reference Toro2016), the metabolic system (D’Angelo Reference D’Angelo2007), the respiratory system (Maury Reference Maury2013, Wall et al. Reference Wall, Wiechert, Comerford and Rausch2010, Trenhago et al. Reference Trenhago, Fernandes, Müller, Blanco and Feijóo2016), the cerebro-spinal fluid circulation (Fin and Grebe Reference Fin and Grebe2003), the nervous system (Liang and Liu Reference Liang and Liu2006), and the lymphatic system (Margaris and Black Reference Margaris and Black2012). For some of them (e.g. the venous and respiratory systems) research has made remarkable progress in recent years. Nonetheless, the mathematical investigation of these systems is still in its infancy; in particular, their coupling with the cardiovascular system is almost absent. Many research avenues are open to the contribution of both pure and applied mathematicians, with the dream of enabling mathematical achievements to play a decisive role in everyday clinical practice.
Acknowledgements
The authors would like to thank P. Biondetti, M. Domanin, L. Forzenigo (Fondazione IRCSS Ca’ Granda, Ospedale Maggiore Policlinico, Milan, Italy), S. Ippolito, R. Scrofani (Ospedale Sacco, Milan, Italy), D. Catanzariti, M. Centonze (Ospedale S. Maria del Carmine, Rovereto (TN), Italy), for providing the radiological images; G. Aloe (Politecnico di Milano) for his help in preparing the figures; D. Bonomi, B. Guerciotti, R.M. Lancellotti, S. Pagani (Politecnico di Milano), D. Forti, F. Negri (EPFL, Lausanne, Switzerland), L. Barbarotta (Technische Universiteit Eindhoven), E. Faggiano (University of Pavia) for their help in preparing the plots of some numerical results; E. Faggiano for her fruitful suggestions. AQ acknowledges the project ‘Integrative HPC Framework for Coupled Cardiac Simulations’ (IFCCS) within the PASC (Platform for Advanced Scientific Computing) network ‘Life Sciences Across Scales’ and the Swiss National Supercomputing Centre (CSCS), project ID s635. CV was partially supported by INDAM-GNCS and by the Italian MIUR PRIN12 project 201289 A4XL. Last but not least, the authors warmly thank Glennis Starling for her fantastic editorial job.